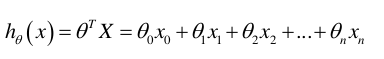Python实现多元线性回归
线性回归介绍
线性回归是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,运用十分广泛。其表达形式为y = w'x+e,e为误差服从均值为0的正态分布。回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。
线性回归属于回归问题。对于回归问题,解决流程为:
给定数据集中每个样本及其正确答案,选择一个模型函数h(hypothesis,假设),并为h找到适应数据的(未必是全局)最优解,即找出最优解下的h的参数。这里给定的数据集取名叫训练集(Training Set)。不能所有数据都拿来训练,要留一部分验证模型好不好使,这点以后说。先列举几个几个典型的模型:
● 最基本的单变量线性回归:
形如h(x)=theta0+theta1*x1
● 多变量线性回归:
形如h(x)=theta0+theta1*x1+theta2*x2+theta3*x3
● 多项式回归(Polynomial Regression):
形如h(x)=theta0+theta1*x1+theta2*(x2^2)+theta3*(x3^3)
或者h(x)=ttheta0+theta1*x1+theta2*sqr(x2)
但是可以令x2=x2^2,x3=x3^3,于是又将其转化为了线性回归模型。虽然不能说多项式回归问题属于线性回归问题,但是一般我们就是这么做的。
● 所以最终通用表达式就是:
数据导入与清洗
对于数据导入来说,可以利用pandas内的read_csv的函数来对数据进行导入操作,在进行多元线性回归之间通过简单线性回归来展现线性回归的特性和结果之后再延伸至多元线性回归。
在进行数据导入之间需要导入进行线性回归的包:
-
import pandas
as pd
-
import numpy
as np
-
import matplotlib.pyplot
as plt
-
from pandas
import DataFrame,Series
-
from sklearn.cross_validation
import train_test_split
-
from sklearn.linear_model
import LinearRegression
我们利用pandas和numpy对数据进行操作,使用matplotlib进行图像化,使用sklearn进行数据集训练与模型导入。
简单线性回归
对于学生来说,所学习的时间和考试的成绩挂钩,所学习的时间与考试的成绩也是呈线性相关。创建一个数据集来描述学生学习时间与成绩的关系并且做简单的线性回归。
in:
-
#创建数据集
-
examDict = {
'学习时间':[
0.50,
0.75,
1.00,
1.25,
1.50,
1.75,
1.75,
-
2.00,
2.25,
2.50,
2.75,
3.00,
3.25,
3.50,
4.00,
4.25,
4.50,
4.75,
5.00,
5.50],
-
'分数':[
10,
22,
13,
43,
20,
22,
33,
50,
62,
-
48,
55,
75,
62,
73,
81,
76,
64,
82,
90,
93]}
-
-
#转换为DataFrame的数据格式
-
examDf = DataFrame(examDict)
通过DataFrame的函数将字典转化为所需要的数据集,也就是学生成绩与考试成绩的数据集。且关于pandas的数据内容Series与DataFrame可以查看关于pandas的博客了解点击打开链接
out:
-
分数 学习时间
-
0
10
0.50
-
1
22
0.75
-
2
13
1.00
-
3
43
1.25
-
4
20
1.50
-
5
22
1.75
-
6
33
1.75
-
7
50
2.00
-
8
62
2.25
-
9
48
2.50
-
10
55
2.75
-
11
75
3.00
-
12
62
3.25
-
13
73
3.50
-
14
81
4.00
-
15
76
4.25
-
16
64
4.50
-
17
82
4.75
-
18
90
5.00
-
19
93
5.50
从上面的数据可以看到数据的特征值与其标签,学生所学习的时间就是所需要的特征值,而成绩就是通过特征值所反应的标签。在这个案例中要对数据进行观测来反应学习时间与成绩的情况,将利用散点图来实现简单的观测。
in:
-
#绘制散点图
-
plt.scatter(examDf.分数,examDf.学习时间,color =
'b',label =
"Exam Data")
-
-
#添加图的标签(x轴,y轴)
-
plt.xlabel(
"Hours")
-
plt.ylabel(
"Score")
-
#显示图像
-
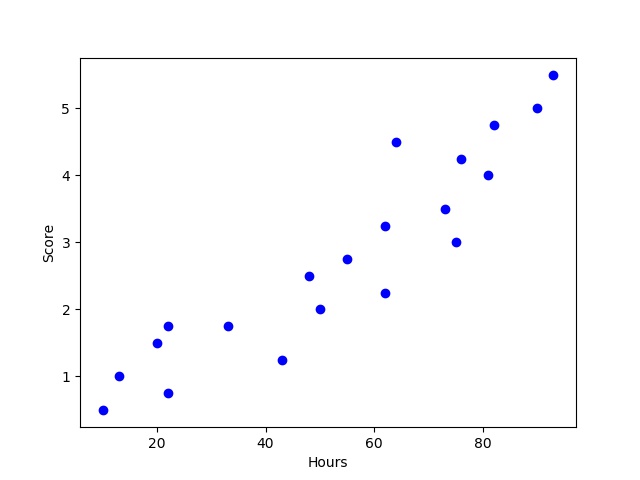
plt.show()
out:
从上图可以看到对于分数和时间来说存在相应的线性关系,且俩数据间相关性较强。
在此可以通过相关性来衡量两个变量因素的相关密切程度。
相关系数是用以反映变量之间相关关系密切程度的统计指标。
r(相关系数) = x和y的协方差/(x的标准差*y的标准差) == cov(x,y)/σx*σy(即person系数)
对于相关性强度来说的化有以下的关系:
0~0.3 弱相关
0.3~0.6 中等程度相关
0.6~1 强相关
in:
out:
-
分数 学习时间
-
分数
1.000000
0.923985
-
学习时间
0.923985
1.000000
pandas中的数学统计函数D.corr()可以反应数据间的相关性关系,可从表值中反应出学习时间与分数之间的相关性为强相关(0.6~1)。对于简单线性回归来来说,简单回归方程为: y = a + b*x (模型建立最佳拟合线)最佳拟合线也是需要通过最小二乘法来实现其作用。对于OLS即最小二乘法我们需要知道的一个关系为点误差,点误差 = 实际值 - 预测值,而误差平方和(Sum of square error) SSE = Σ(实际值-预测值)^2,最小二乘法就是基于SSE实现,最小二乘法 : 使得误差平方和最小(最佳拟合)。解释完简单线性回归后进行对训练集和测试集的创建,将会使用train_test_split函数来创建(train_test_split是存在与sklearn中的函数)
in:
-
#将原数据集拆分训练集和测试集
-
X_train,X_test,Y_train,Y_test = train_test_split(exam_X,exam_Y,train_size=
.8)
-
#X_train为训练数据标签,X_test为测试数据标签,exam_X为样本特征,exam_y为样本标签,train_size 训练数据占比
-
-
print(
"原始数据特征:",exam_X.shape,
-
",训练数据特征:",X_train.shape,
-
",测试数据特征:",X_test.shape)
-
-
print(
"原始数据标签:",exam_Y.shape,
-
",训练数据标签:",Y_train.shape,
-
",测试数据标签:",Y_test.shape)
-
-
#散点图
-
plt.scatter(X_train, Y_train, color=
"blue", label=
"train data")
-
plt.scatter(X_test, Y_test, color=
"red", label=
"test data")
-
-
#添加图标标签
-
plt.legend(loc=
2)
-
plt.xlabel(
"Hours")
-
plt.ylabel(
"Pass")
-
#显示图像
-
plt.savefig(
"tests.jpg")
-
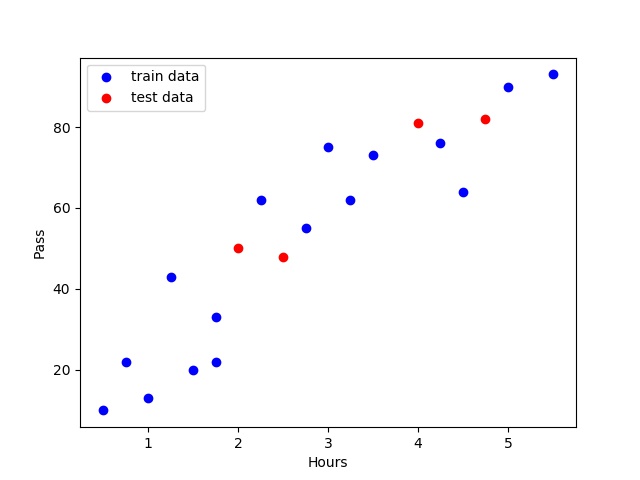
plt.show()
out:
-
原始数据特征: (
20,) ,训练数据特征: (
16,) ,测试数据特征: (
4,)
-
原始数据标签: (
20,) ,训练数据标签: (
16,) ,测试数据标签: (
4,)
tips:由于训练集随机分配的原因每一次运行的结果(点的分布情况,训练集内的情况,测试集内的情况)不都相同在创建数据集之后我们需要将训练集放入skleran中的线性回归模型(LinearRegression())进行训练,使用函数种的.fit函数进行模型的训练操作。
in:
-
model = LinearRegression()
-
-
#对于模型错误我们需要把我们的训练集进行reshape操作来达到函数所需要的要求
-
# model.fit(X_train,Y_train)
-
-
#reshape如果行数=-1的话可以使我们的数组所改的列数自动按照数组的大小形成新的数组
-
#因为model需要二维的数组来进行拟合但是这里只有一个特征所以需要reshape来转换为二维数组
-
X_train = X_train.values.reshape(
-1,
1)
-
X_test = X_test.values.reshape(
-1,
1)
-
-
model.fit(X_train,Y_train)
在模型训练完成之后会得到所对应的方程式(线性回归方程式)需要利用函数中的intercept_与coef_来得到
-
a = model.intercept_
#截距
-
-
b = model.coef_
#回归系数
-
-
print(
"最佳拟合线:截距",a,
",回归系数:",b)
out:
最佳拟合线:截距 7.5580754557 ,回归系数: [ 16.28401865]
由上述的最佳拟合线的截距和回归系数可以算出其线性回归线方程:y = 7.56 + 16.28*x
接下来需要对模型进行预测和对模型进行评价,在进行评价之间将会引入一个决定系数r平方的概念。
对于决定系数R平方常用于评估模型的精确度。
下列为R平方的计算公式:
● y误差平方和 = Σ(y实际值 - y预测值)^2
● y的总波动 = Σ(y实际值 - y平均值)^2
● 有多少百分比的y波动没有被回归拟合线所描述 = SSE/总波动
● 有多少百分比的y波动被回归线描述 = 1 - SSE/总波动 = 决定系数R平方
对于决定系数R平方来说
(1) 回归线拟合程度:有多少百分比的y波动刻印有回归线来描述(x的波动变化)
(2)值大小:R平方越高,回归模型越精确(取值范围0~1),1无误差,0无法完成拟合对于预测来说我们需要运用函数中的model.predict()来得到预测值
in:
-
#训练数据的预测值
-
y_train_pred = model.predict(X_train)
-
#绘制最佳拟合线:标签用的是训练数据的预测值y_train_pred
-
plt.plot(X_train, y_train_pred, color=
'black', linewidth=
3, label=
"best line")
-
-
#测试数据散点图
-
plt.scatter(X_test, Y_test, color=
'red', label=
"test data")
-
-
#添加图标标签
-
plt.legend(loc=
2)
-
plt.xlabel(
"Hours")
-
plt.ylabel(
"Score")
-
#显示图像
-
plt.savefig(
"lines.jpg")
-
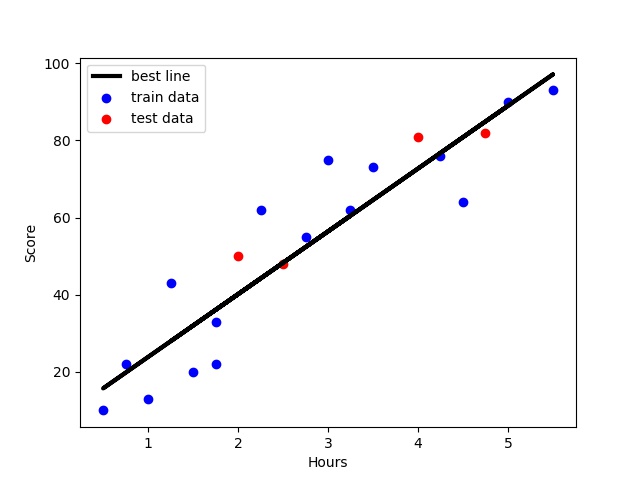
plt.show()
-
-
-
score = model.score(X_test,Y_test)
-
-
print(score)
out:
score : 0.834706696876
多元线性回归
在间单线性回归的例子中可以得到与线性回归相关的分析流程,接下来对多元线性回归进行分析对于多元线性回归前面已经提到,形如h(x)=theta0+theta1*x1+theta2*x2+theta3*x3从http://www-bcf.usc.edu/~gareth/ISL/Advertising.csv(已经失效)来下载数据集 Advertising.csv,其数据描述了一个产品的销量与广告媒体的投入之间影响。将会利用pandas的pd.read()来读取数据。
in:
-
#通过read_csv来读取我们的目的数据集
-
adv_data = pd.read_csv(
"C:/Users/Administrator/Desktop/Advertising.csv")
-
#清洗不需要的数据
-
new_adv_data = adv_data.ix[:,
1:]
-
#得到我们所需要的数据集且查看其前几列以及数据形状
-
print(
'head:',new_adv_data.head(),
'\nShape:',new_adv_data.shape)
out:
-
head: TV radio newspaper sales
-
0
230.1
37.8
69.2
22.1
-
1
44.5
39.3
45.1
10.4
-
2
17.2
45.9
69.3
9.3
-
3
151.5
41.3
58.5
18.5
-
4
180.8
10.8
58.4
12.9
-
Shape: (
200,
4)
对于上述的数据可以得到数据中
标签值(sales):
- Sales:对应产品的销量
特征值(TV,Radio,Newspaper):
- TV:对于一个给定市场中单一产品,用于电视上的广告费用(以千为单位)
- Radio:在广播媒体上投资的广告费用
- Newspaper:用于报纸媒体的广告费用
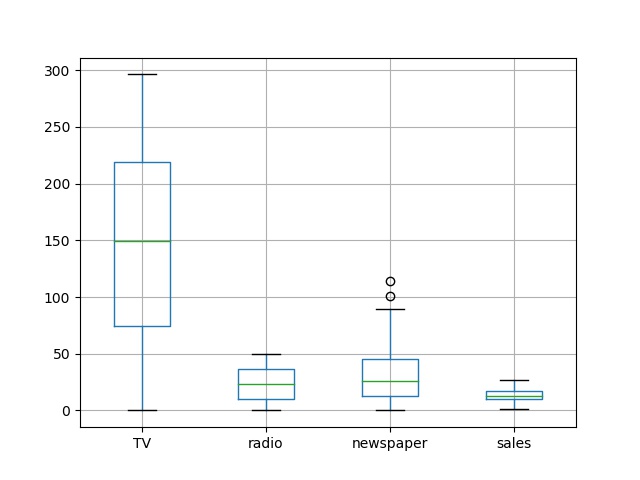
在这个案例中,通过不同的广告投入,预测产品销量。因为响应变量是一个连续的值,所以这个问题是一个回归问题。数据集一共有200个观测值,每一组观测对应一个市场的情况。接下里对数据进行描述性统计,以及寻找缺失值(缺失值对模型的影响较大,如发现缺失值应替换或删除),且利用箱图来从可视化方面来查看数据集,在描述统计之后对数据进行相关性分析,以此来查找数据中特征值与标签值之间的关系。
in:
-
#数据描述
-
print(new_adv_data.describe())
-
#缺失值检验
-
print(new_adv_data[new_adv_data.isnull()==
True].count())
-
-
new_adv_data.boxplot()
-
plt.savefig(
"boxplot.jpg")
-
plt.show()
-
##相关系数矩阵 r(相关系数) = x和y的协方差/(x的标准差*y的标准差) == cov(x,y)/σx*σy
-
#相关系数0~0.3弱相关0.3~0.6中等程度相关0.6~1强相关
-
print(new_adv_data.corr())
out:
-
TV radio newspaper sales
-
count
200.000000
200.000000
200.000000
200.000000
-
mean
147.042500
23.264000
30.554000
14.022500
-
std
85.854236
14.846809
21.778621
5.217457
-
min
0.700000
0.000000
0.300000
1.600000
-
25%
74.375000
9.975000
12.750000
10.375000
-
50%
149.750000
22.900000
25.750000
12.900000
-
75%
218.825000
36.525000
45.100000
17.400000
-
max
296.400000
49.600000
114.000000
27.000000
-
TV
0
-
radio
0
-
newspaper
0
-
sales
0
-
dtype: int64
-
TV radio newspaper sales
-
TV
1.000000
0.054809
0.056648
0.782224
-
radio
0.054809
1.000000
0.354104
0.576223
-
newspaper
0.056648
0.354104
1.000000
0.228299
-
sales
0.782224
0.576223
0.228299
1.000000
可以从corr表中看出,TV特征和销量是有比较强的线性关系的,而Radio和Sales线性关系弱一些但是也是属于强相关的,Newspaper和Sales线性关系更弱。接下来建立散点图来查看数据里的数据分析情况以及对相对应的线性情况,将使用seaborn的pairplot来绘画3种不同的因素对标签值的影响
in:
-
# 通过加入一个参数kind='reg',seaborn可以添加一条最佳拟合直线和95%的置信带。
-
sns.pairplot(new_adv_data, x_vars=[
'TV',
'radio',
'newspaper'], y_vars=
'sales', size=
7, aspect=
0.8,kind =
'reg')
-
plt.savefig(
"pairplot.jpg")
-
plt.show()
out:
上如图种所示,可以了解到不同的因素对销量的预测线(置信度= 95 %),也可可以大致看出不同特征对于标签值的影响与相关关系在了解了数据的各种情况后需要对数据集建立模型,在建立模型的第一步我们将建立训练集与测试集同样的将会使用train_test_split函数来创建(train_test_split是存在与sklearn中的函数)
in:
-
X_train,X_test,Y_train,Y_test = train_test_split(new_adv_data.ix[:,:
3],new_adv_data.sales,train_size=
.80)
-
-
print(
"原始数据特征:",new_adv_data.ix[:,:
3].shape,
-
",训练数据特征:",X_train.shape,
-
",测试数据特征:",X_test.shape)
-
-
print(
"原始数据标签:",new_adv_data.sales.shape,
-
",训练数据标签:",Y_train.shape,
-
",测试数据标签:",Y_test.shape)
out:
-
原始数据特征: (
200,
3) ,训练数据特征: (
160,
3) ,测试数据特征: (
40,
3)
-
原始数据标签: (
200,) ,训练数据标签: (
160,) ,测试数据标签: (
40,)
建立初步的数据集模型之后将训练集中的特征值与标签值放入LinearRegression()模型中且使用fit函数进行训练,在模型训练完成之后会得到所对应的方程式(线性回归方程式)需要利用函数中的intercept_与coef_。
in:
-
model = LinearRegression()
-
-
model.fit(X_train,Y_train)
-
-
a = model.intercept_
#截距
-
-
b = model.coef_
#回归系数
-
-
print(
"最佳拟合线:截距",a,
",回归系数:",b)
out:
最佳拟合线:截距 2.79361553401 ,回归系数: [ 0.04711495 0.18719875 -0.00185999]
即所得的多元线性回归模型的函数为 : y = 2.79 + 0.04 * TV + 0.187 * Radio - 0.002 * Newspaper,对于给定了Radio和Newspaper的广告投入,如果在TV广告上每多投入1个单位,对应销量将增加0.04711个单位。就是加入其它两个媒体投入固定,在TV广告上每增加1000美元(因为单位是1000美元),销量将增加47.11(因为单位是1000)。但是大家注意这里的newspaper的系数居然是负数,所以我们可以考虑不使用newspaper这个特征。接下来对数据集进行预测与模型测评。同样使用predict与score函数来获取所需要的预测值与得分。
in:
-
#R方检测
-
#决定系数r平方
-
#对于评估模型的精确度
-
#y误差平方和 = Σ(y实际值 - y预测值)^2
-
#y的总波动 = Σ(y实际值 - y平均值)^2
-
#有多少百分比的y波动没有被回归拟合线所描述 = SSE/总波动
-
#有多少百分比的y波动被回归线描述 = 1 - SSE/总波动 = 决定系数R平方
-
#对于决定系数R平方来说1) 回归线拟合程度:有多少百分比的y波动刻印有回归线来描述(x的波动变化)
-
#2)值大小:R平方越高,回归模型越精确(取值范围0~1),1无误差,0无法完成拟合
-
score = model.score(X_test,Y_test)
-
-
print(score)
-
-
#对线性回归进行预测
-
-
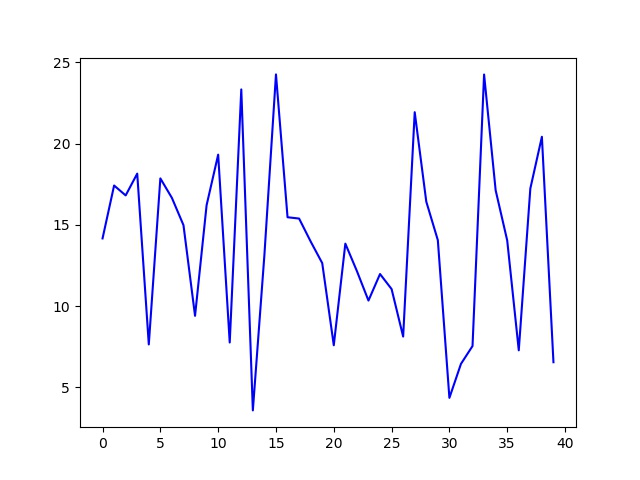
Y_pred = model.predict(X_test)
-
-
print(Y_pred)
-
-
plt.plot(range(len(Y_pred)),Y_pred,
'b',label=
"predict")
-
#显示图像
-
plt.savefig(
"predict.jpg")
-
plt.show()
out:
-
score :
0.871755480886
-
predict :[
14.17217173
17.42866884
16.81933374
18.16079802
7.64784604
-
17.8670496
16.66488531
14.98782916
9.41023763
16.21679696
-
19.32696651
7.76788593
23.34231219
3.59006148
13.15777984
-
24.26609169
15.47571902
15.39542342
13.98430709
12.65446708
-
7.59818691
13.85179898
12.16325619
10.34902817
11.9813427
-
11.05726513
8.13405159
21.94038306
16.4388483
14.06506403
-
4.36052153
6.45326681
7.55083036
24.25987365
17.13603444
-
14.04814117
7.28664465
17.24163581
20.42745536
6.55512244]
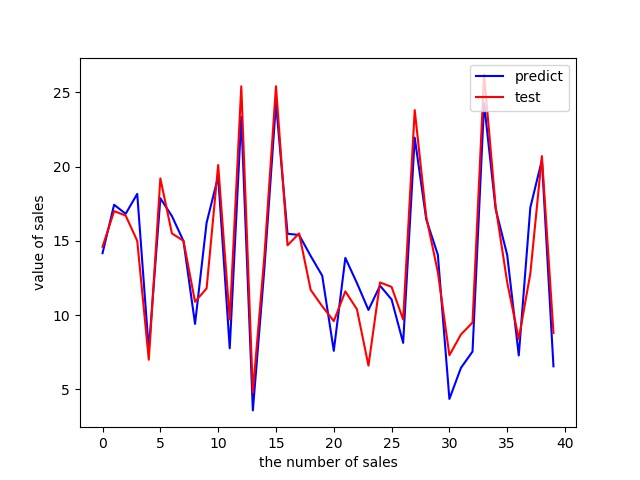
预测集与源数据集的对比如下:
模型的检测方法-ROC曲线:
ROC曲线是根据一系列不同的二分类方式(分界值或决定阈),以真阳性率(灵敏度)为纵坐标,假阳性率(1-特异度)为横坐标绘制的曲线。传统的诊断试验评价方法有一个共同的特点,必须将试验结果分为两类,再进行统计分析。ROC曲线的评价方法与传统的评价方法不同,无须此限制,而是根据实际情况,允许有中间状态,可以把试验结果划分为多个有序分类,如正常、大致正常、可疑、大致异常和异常五个等级再进行统计分析。因此,ROC曲线评价方法适用的范围更为广泛。
1.ROC曲线能很容易地查出任意界限值时的对疾病的识别能力。
2.选择最佳的诊断界限值。ROC曲线越靠近左上角,试验的准确性就越高。最靠近左上角的ROC曲线的点是错误最少的最好阈值,其假阳性和假阴性的总数最少。
3.两种或两种以上不同诊断试验对疾病识别能力的比较。在对同一种疾病的两种或两种以上诊断方法进行比较时,可将各试验的ROC曲线绘制到同一坐标中,以直观地鉴别优劣,靠近左上角的ROC曲线所代表的受试者工作最准确。亦可通过分别计算各个试验的ROC曲线下的面积(AUC)进行比较,哪一种试验的 AUC最大,则哪一种试验的诊断价值最佳(百度百科)
模型提升:
对于提升模型准确度的方法很多,在这个模型下,可以利用异常值替换,将Newspaper中的异常值进行拉格朗日法插补,朗格朗日插补法(from scipy.interpolate import lagrange即scipy中的函数)可以间接提高模型的准确度,如果不需要插补异常值或缺失值的话可以将Newspaper不列为特征值考虑,在不考虑Newspaper为特征值的情况下,新的模型的准确率将超过旧模型,也可以从模型的准确度来反证Newspaper不适合作为特征值。
整体代码如下,数据集再上面链接中可直接下载。
-
import pandas
as pd
-
import numpy
as np
-
import matplotlib.pyplot
as plt
-
from pandas
import DataFrame,Series
-
from sklearn.cross_validation
import train_test_split
-
from sklearn.linear_model
import LinearRegression
-
#创建数据集
-
examDict = {
'学习时间':[
0.50,
0.75,
1.00,
1.25,
1.50,
1.75,
1.75,
-
2.00,
2.25,
2.50,
2.75,
3.00,
3.25,
3.50,
4.00,
4.25,
4.50,
4.75,
5.00,
5.50],
-
'分数':[
10,
22,
13,
43,
20,
22,
33,
50,
62,
-
48,
55,
75,
62,
73,
81,
76,
64,
82,
90,
93]}
-
-
#转换为DataFrame的数据格式
-
examDf = DataFrame(examDict)
-
-
#绘制散点图
-
plt.scatter(examDf.分数,examDf.学习时间,color =
'b',label =
"Exam Data")
-
-
#添加图的标签(x轴,y轴)
-
plt.xlabel(
"Hours")
-
plt.ylabel(
"Score")
-
#显示图像
-
plt.savefig(
"examDf.jpg")
-
plt.show()
-
-
-
#相关系数矩阵 r(相关系数) = x和y的协方差/(x的标准差*y的标准差) == cov(x,y)/σx*σy
-
#相关系数0~0.3弱相关0.3~0.6中等程度相关0.6~1强相关
-
rDf = examDf.corr()
-
print(rDf)
-
-
#回归方程 y = a + b*x (模型建立最佳拟合线)
-
#点误差 = 实际值 - 拟合值
-
#误差平方和(Sum of square error) SSE = Σ(实际值-预测值)^2
-
#最小二乘法 : 使得误差平方和最小(最佳拟合)
-
exam_X = examDf.loc[:,
'学习时间']
-
exam_Y = examDf.loc[:,
'分数']
-
-
#将原数据集拆分训练集和测试集
-
X_train,X_test,Y_train,Y_test = train_test_split(exam_X,exam_Y,train_size=
.8)
-
#X_train为训练数据标签,X_test为测试数据标签,exam_X为样本特征,exam_y为样本标签,train_size 训练数据占比
-
-
print(
"原始数据特征:",exam_X.shape,
-
",训练数据特征:",X_train.shape,
-
",测试数据特征:",X_test.shape)
-
-
print(
"原始数据标签:",exam_Y.shape,
-
",训练数据标签:",Y_train.shape,
-
",测试数据标签:",Y_test.shape)
-
-
#散点图
-
plt.scatter(X_train, Y_train, color=
"blue", label=
"train data")
-
plt.scatter(X_test, Y_test, color=
"red", label=
"test data")
-
-
#添加图标标签
-
plt.legend(loc=
2)
-
plt.xlabel(
"Hours")
-
plt.ylabel(
"Pass")
-
#显示图像
-
plt.savefig(
"tests.jpg")
-
plt.show()
-
-
-
-
model = LinearRegression()
-
-
#对于下面的模型错误我们需要把我们的训练集进行reshape操作来达到函数所需要的要求
-
# model.fit(X_train,Y_train)
-
-
#reshape如果行数=-1的话可以使我们的数组所改的列数自动按照数组的大小形成新的数组
-
#因为model需要二维的数组来进行拟合但是这里只有一个特征所以需要reshape来转换为二维数组
-
X_train = X_train.values.reshape(
-1,
1)
-
X_test = X_test.values.reshape(
-1,
1)
-
-
model.fit(X_train,Y_train)
-
-
a = model.intercept_
#截距
-
-
b = model.coef_
#回归系数
-
-
print(
"最佳拟合线:截距",a,
",回归系数:",b)
-
-
#决定系数r平方
-
#对于评估模型的精确度
-
#y误差平方和 = Σ(y实际值 - y预测值)^2
-
#y的总波动 = Σ(y实际值 - y平均值)^2
-
#有多少百分比的y波动没有被回归拟合线所描述 = SSE/总波动
-
#有多少百分比的y波动被回归线描述 = 1 - SSE/总波动 = 决定系数R平方
-
#对于决定系数R平方来说1) 回归线拟合程度:有多少百分比的y波动刻印有回归线来描述(x的波动变化)
-
#2)值大小:R平方越高,回归模型越精确(取值范围0~1),1无误差,0无法完成拟合
-
-
plt.scatter(X_train, Y_train, color=
'blue', label=
"train data")
-
-
#训练数据的预测值
-
y_train_pred = model.predict(X_train)
-
#绘制最佳拟合线:标签用的是训练数据的预测值y_train_pred
-
plt.plot(X_train, y_train_pred, color=
'black', linewidth=
3, label=
"best line")
-
-
#测试数据散点图
-
plt.scatter(X_test, Y_test, color=
'red', label=
"test data")
-
-
#添加图标标签
-
plt.legend(loc=
2)
-
plt.xlabel(
"Hours")
-
plt.ylabel(
"Score")
-
#显示图像
-
plt.savefig(
"lines.jpg")
-
plt.show()
-
-
-
score = model.score(X_test,Y_test)
-
-
print(score)
-
import pandas
as pd
-
import seaborn
as sns
-
from sklearn.linear_model
import LinearRegression
-
import matplotlib.pyplot
as plt
-
from sklearn.cross_validation
import train_test_split
-
-
#通过read_csv来读取我们的目的数据集
-
adv_data = pd.read_csv(
"C:/Users/Administrator/Desktop/Advertising.csv")
-
#清洗不需要的数据
-
new_adv_data = adv_data.ix[:,
1:]
-
#得到我们所需要的数据集且查看其前几列以及数据形状
-
print(
'head:',new_adv_data.head(),
'\nShape:',new_adv_data.shape)
-
-
#数据描述
-
print(new_adv_data.describe())
-
#缺失值检验
-
print(new_adv_data[new_adv_data.isnull()==
True].count())
-
-
new_adv_data.boxplot()
-
plt.savefig(
"boxplot.jpg")
-
plt.show()
-
##相关系数矩阵 r(相关系数) = x和y的协方差/(x的标准差*y的标准差) == cov(x,y)/σx*σy
-
#相关系数0~0.3弱相关0.3~0.6中等程度相关0.6~1强相关
-
print(new_adv_data.corr())
-
-
#建立散点图来查看数据集里的数据分布
-
#seaborn的pairplot函数绘制X的每一维度和对应Y的散点图。通过设置size和aspect参数来调节显示的大小和比例。
-
# 可以从图中看出,TV特征和销量是有比较强的线性关系的,而Radio和Sales线性关系弱一些,Newspaper和Sales线性关系更弱。
-
# 通过加入一个参数kind='reg',seaborn可以添加一条最佳拟合直线和95%的置信带。
-
sns.pairplot(new_adv_data, x_vars=[
'TV',
'radio',
'newspaper'], y_vars=
'sales', size=
7, aspect=
0.8,kind =
'reg')
-
plt.savefig(
"pairplot.jpg")
-
plt.show()
-
-
#利用sklearn里面的包来对数据集进行划分,以此来创建训练集和测试集
-
#train_size表示训练集所占总数据集的比例
-
X_train,X_test,Y_train,Y_test = train_test_split(new_adv_data.ix[:,:
3],new_adv_data.sales,train_size=
.80)
-
-
print(
"原始数据特征:",new_adv_data.ix[:,:
3].shape,
-
",训练数据特征:",X_train.shape,
-
",测试数据特征:",X_test.shape)
-
-
print(
"原始数据标签:",new_adv_data.sales.shape,
-
",训练数据标签:",Y_train.shape,
-
",测试数据标签:",Y_test.shape)
-
-
model = LinearRegression()
-
-
model.fit(X_train,Y_train)
-
-
a = model.intercept_
#截距
-
-
b = model.coef_
#回归系数
-
-
print(
"最佳拟合线:截距",a,
",回归系数:",b)
-
#y=2.668+0.0448∗TV+0.187∗Radio-0.00242∗Newspaper
-
-
#R方检测
-
#决定系数r平方
-
#对于评估模型的精确度
-
#y误差平方和 = Σ(y实际值 - y预测值)^2
-
#y的总波动 = Σ(y实际值 - y平均值)^2
-
#有多少百分比的y波动没有被回归拟合线所描述 = SSE/总波动
-
#有多少百分比的y波动被回归线描述 = 1 - SSE/总波动 = 决定系数R平方
-
#对于决定系数R平方来说1) 回归线拟合程度:有多少百分比的y波动刻印有回归线来描述(x的波动变化)
-
#2)值大小:R平方越高,回归模型越精确(取值范围0~1),1无误差,0无法完成拟合
-
score = model.score(X_test,Y_test)
-
-
print(score)
-
-
#对线性回归进行预测
-
-
Y_pred = model.predict(X_test)
-
-
print(Y_pred)
-
-
-
plt.plot(range(len(Y_pred)),Y_pred,
'b',label=
"predict")
-
#显示图像
-
# plt.savefig("predict.jpg")
-
plt.show()
-
-
plt.figure()
-
plt.plot(range(len(Y_pred)),Y_pred,
'b',label=
"predict")
-
plt.plot(range(len(Y_pred)),Y_test,
'r',label=
"test")
-
plt.legend(loc=
"upper right")
#显示图中的标签
-
plt.xlabel(
"the number of sales")
-
plt.ylabel(
'value of sales')
-
plt.savefig(
"ROC.jpg")
-
plt.show()
-
-
-
-
Advertising.csv的连接已经失效,以下是补充的数据,可复制粘贴到CSV进行保存
| TV | radio | newspaper | sales |
| 230.1 | 37.8 | 69.2 | 22.1 |
| 44.5 | 39.3 | 45.1 | 10.4 |
| 17.2 | 45.9 | 69.3 | 9.3 |
| 151.5 | 41.3 | 58.5 | 18.5 |
| 180.8 | 10.8 | 58.4 | 12.9 |
| 8.7 | 48.9 | 75 | 7.2 |
| 57.5 | 32.8 | 23.5 | 11.8 |
| 120.2 | 19.6 | 11.6 | 13.2 |
| 8.6 | 2.1 | 1 | 4.8 |
| 199.8 | 2.6 | 21.2 | 10.6 |
| 66.1 | 5.8 | 24.2 | 8.6 |
| 214.7 | 24 | 4 | 17.4 |
| 23.8 | 35.1 | 65.9 | 9.2 |
| 97.5 | 7.6 | 7.2 | 9.7 |
| 204.1 | 32.9 | 46 | 19 |
| 195.4 | 47.7 | 52.9 | 22.4 |
| 67.8 | 36.6 | 114 | 12.5 |
| 281.4 | 39.6 | 55.8 | 24.4 |
| 69.2 | 20.5 | 18.3 | 11.3 |
| 147.3 | 23.9 | 19.1 | 14.6 |
| 218.4 | 27.7 | 53.4 | 18 |
| 237.4 | 5.1 | 23.5 | 12.5 |
| 13.2 | 15.9 | 49.6 | 5.6 |
| 228.3 | 16.9 | 26.2 | 15.5 |
| 62.3 | 12.6 | 18.3 | 9.7 |
| 262.9 | 3.5 | 19.5 | 12 |
| 142.9 | 29.3 | 12.6 | 15 |
| 240.1 | 16.7 | 22.9 | 15.9 |
| 248.8 | 27.1 | 22.9 | 18.9 |
| 70.6 | 16 | 40.8 | 10.5 |
| 292.9 | 28.3 | 43.2 | 21.4 |
| 112.9 | 17.4 | 38.6 | 11.9 |
| 97.2 | 1.5 | 30 | 9.6 |
| 265.6 | 20 | 0.3 | 17.4 |
| 95.7 | 1.4 | 7.4 | 9.5 |
| 290.7 | 4.1 | 8.5 | 12.8 |
| 266.9 | 43.8 | 5 | 25.4 |
| 74.7 | 49.4 | 45.7 | 14.7 |
| 43.1 | 26.7 | 35.1 | 10.1 |
| 228 | 37.7 | 32 | 21.5 |
| 202.5 | 22.3 | 31.6 | 16.6 |
| 177 | 33.4 | 38.7 | 17.1 |
| 293.6 | 27.7 | 1.8 | 20.7 |
| 206.9 | 8.4 | 26.4 | 12.9 |
| 25.1 | 25.7 | 43.3 | 8.5 |
| 175.1 | 22.5 | 31.5 | 14.9 |
| 89.7 | 9.9 | 35.7 | 10.6 |
| 239.9 | 41.5 | 18.5 | 23.2 |
| 227.2 | 15.8 | 49.9 | 14.8 |
| 66.9 | 11.7 | 36.8 | 9.7 |
| 199.8 | 3.1 | 34.6 | 11.4 |
| 100.4 | 9.6 | 3.6 | 10.7 |
| 216.4 | 41.7 | 39.6 | 22.6 |
| 182.6 | 46.2 | 58.7 | 21.2 |
| 262.7 | 28.8 | 15.9 | 20.2 |
| 198.9 | 49.4 | 60 | 23.7 |
| 7.3 | 28.1 | 41.4 | 5.5 |
| 136.2 | 19.2 | 16.6 | 13.2 |
| 210.8 | 49.6 | 37.7 | 23.8 |
| 210.7 | 29.5 | 9.3 | 18.4 |
| 53.5 | 2 | 21.4 | 8.1 |
| 261.3 | 42.7 | 54.7 | 24.2 |
| 239.3 | 15.5 | 27.3 | 15.7 |
| 102.7 | 29.6 | 8.4 | 14 |
| 131.1 | 42.8 | 28.9 | 18 |
| 69 | 9.3 | 0.9 | 9.3 |
| 31.5 | 24.6 | 2.2 | 9.5 |
| 139.3 | 14.5 | 10.2 | 13.4 |
| 237.4 | 27.5 | 11 | 18.9 |
| 216.8 | 43.9 | 27.2 | 22.3 |
| 199.1 | 30.6 | 38.7 | 18.3 |
| 109.8 | 14.3 | 31.7 | 12.4 |
| 26.8 | 33 | 19.3 | 8.8 |
| 129.4 | 5.7 | 31.3 | 11 |
| 213.4 | 24.6 | 13.1 | 17 |
| 16.9 | 43.7 | 89.4 | 8.7 |
| 27.5 | 1.6 | 20.7 | 6.9 |
| 120.5 | 28.5 | 14.2 | 14.2 |
| 5.4 | 29.9 | 9.4 | 5.3 |
| 116 | 7.7 | 23.1 | 11 |
| 76.4 | 26.7 | 22.3 | 11.8 |
| 239.8 | 4.1 | 36.9 | 12.3 |
| 75.3 | 20.3 | 32.5 | 11.3 |
| 68.4 | 44.5 | 35.6 | 13.6 |
| 213.5 | 43 | 33.8 | 21.7 |
| 193.2 | 18.4 | 65.7 | 15.2 |
| 76.3 | 27.5 | 16 | 12 |
| 110.7 | 40.6 | 63.2 | 16 |
| 88.3 | 25.5 | 73.4 | 12.9 |
| 109.8 | 47.8 | 51.4 | 16.7 |
| 134.3 | 4.9 | 9.3 | 11.2 |
| 28.6 | 1.5 | 33 | 7.3 |
| 217.7 | 33.5 | 59 | 19.4 |
| 250.9 | 36.5 | 72.3 | 22.2 |
| 107.4 | 14 | 10.9 | 11.5 |
| 163.3 | 31.6 | 52.9 | 16.9 |
| 197.6 | 3.5 | 5.9 | 11.7 |
| 184.9 | 21 | 22 | 15.5 |
| 289.7 | 42.3 | 51.2 | 25.4 |
| 135.2 | 41.7 | 45.9 | 17.2 |
| 222.4 | 4.3 | 49.8 | 11.7 |
| 296.4 | 36.3 | 100.9 | 23.8 |
| 280.2 | 10.1 | 21.4 | 14.8 |
| 187.9 | 17.2 | 17.9 | 14.7 |
| 238.2 | 34.3 | 5.3 | 20.7 |
| 137.9 | 46.4 | 59 | 19.2 |
| 25 | 11 | 29.7 | 7.2 |
| 90.4 | 0.3 | 23.2 | 8.7 |
| 13.1 | 0.4 | 25.6 | 5.3 |
| 255.4 | 26.9 | 5.5 | 19.8 |
| 225.8 | 8.2 | 56.5 | 13.4 |
| 241.7 | 38 | 23.2 | 21.8 |
| 175.7 | 15.4 | 2.4 | 14.1 |
| 209.6 | 20.6 | 10.7 | 15.9 |
| 78.2 | 46.8 | 34.5 | 14.6 |
| 75.1 | 35 | 52.7 | 12.6 |
| 139.2 | 14.3 | 25.6 | 12.2 |
| 76.4 | 0.8 | 14.8 | 9.4 |
| 125.7 | 36.9 | 79.2 | 15.9 |
| 19.4 | 16 | 22.3 | 6.6 |
| 141.3 | 26.8 | 46.2 | 15.5 |
| 18.8 | 21.7 | 50.4 | 7 |
| 224 | 2.4 | 15.6 | 11.6 |
| 123.1 | 34.6 | 12.4 | 15.2 |
| 229.5 | 32.3 | 74.2 | 19.7 |
| 87.2 | 11.8 | 25.9 | 10.6 |
| 7.8 | 38.9 | 50.6 | 6.6 |
| 80.2 | 0 | 9.2 | 8.8 |
| 220.3 | 49 | 3.2 | 24.7 |
| 59.6 | 12 | 43.1 | 9.7 |
| 0.7 | 39.6 | 8.7 | 1.6 |
| 265.2 | 2.9 | 43 | 12.7 |
| 8.4 | 27.2 | 2.1 | 5.7 |
| 219.8 | 33.5 | 45.1 | 19.6 |
| 36.9 | 38.6 | 65.6 | 10.8 |
| 48.3 | 47 | 8.5 | 11.6 |
| 25.6 | 39 | 9.3 | 9.5 |
| 273.7 | 28.9 | 59.7 | 20.8 |
| 43 | 25.9 | 20.5 | 9.6 |
| 184.9 | 43.9 | 1.7 | 20.7 |
| 73.4 | 17 | 12.9 | 10.9 |
| 193.7 | 35.4 | 75.6 | 19.2 |
| 220.5 | 33.2 | 37.9 | 20.1 |
| 104.6 | 5.7 | 34.4 | 10.4 |
| 96.2 | 14.8 | 38.9 | 11.4 |
| 140.3 | 1.9 | 9 | 10.3 |
| 240.1 | 7.3 | 8.7 | 13.2 |
| 243.2 | 49 | 44.3 | 25.4 |
| 38 | 40.3 | 11.9 | 10.9 |
| 44.7 | 25.8 | 20.6 | 10.1 |
| 280.7 | 13.9 | 37 | 16.1 |
| 121 | 8.4 | 48.7 | 11.6 |
| 197.6 | 23.3 | 14.2 | 16.6 |
| 171.3 | 39.7 | 37.7 | 19 |
| 187.8 | 21.1 | 9.5 | 15.6 |
| 4.1 | 11.6 | 5.7 | 3.2 |
| 93.9 | 43.5 | 50.5 | 15.3 |
| 149.8 | 1.3 | 24.3 | 10.1 |
| 11.7 | 36.9 | 45.2 | 7.3 |
| 131.7 | 18.4 | 34.6 | 12.9 |
| 172.5 | 18.1 | 30.7 | 14.4 |
| 85.7 | 35.8 | 49.3 | 13.3 |
| 188.4 | 18.1 | 25.6 | 14.9 |
| 163.5 | 36.8 | 7.4 | 18 |
| 117.2 | 14.7 | 5.4 | 11.9 |
| 234.5 | 3.4 | 84.8 | 11.9 |
| 17.9 | 37.6 | 21.6 | 8 |
| 206.8 | 5.2 | 19.4 | 12.2 |
| 215.4 | 23.6 | 57.6 | 17.1 |
| 284.3 | 10.6 | 6.4 | 15 |
| 50 | 11.6 | 18.4 | 8.4 |
| 164.5 | 20.9 | 47.4 | 14.5 |
| 19.6 | 20.1 | 17 | 7.6 |
| 168.4 | 7.1 | 12.8 | 11.7 |
| 222.4 | 3.4 | 13.1 | 11.5 |
| 276.9 | 48.9 | 41.8 | 27 |
| 248.4 | 30.2 | 20.3 | 20.2 |
| 170.2 | 7.8 | 35.2 | 11.7 |
| 276.7 | 2.3 | 23.7 | 11.8 |
| 165.6 | 10 | 17.6 | 12.6 |
| 156.6 | 2.6 | 8.3 | 10.5 |
| 218.5 | 5.4 | 27.4 | 12.2 |
| 56.2 | 5.7 | 29.7 | 8.7 |
| 287.6 | 43 | 71.8 | 26.2 |
| 253.8 | 21.3 | 30 | 17.6 |
| 205 | 45.1 | 19.6 | 22.6 |
| 139.5 | 2.1 | 26.6 | 10.3 |
| 191.1 | 28.7 | 18.2 | 17.3 |
| 286 | 13.9 | 3.7 | 15.9 |
| 18.7 | 12.1 | 23.4 | 6.7 |
| 39.5 | 41.1 | 5.8 | 10.8 |
| 75.5 | 10.8 | 6 | 9.9 |
| 17.2 | 4.1 | 31.6 | 5.9 |
| 166.8 | 42 | 3.6 | 19.6 |
| 149.7 | 35.6 | 6 | 17.3 |
| 38.2 | 3.7 | 13.8 | 7.6 |
| 94.2 | 4.9 | 8.1 | 9.7 |
| 177 | 9.3 | 6.4 | 12.8 |
| 283.6 | 42 | 66.2 | 25.5 |
| 232.1 | 8.6 | 8.7 | 13.4 |