构建深度学习模型的基本流程就是：搭建计算图，求得损失函数，然后计算损失函数对模型参数的导数，再利用梯度下降法等方法来更新参数。搭建计算图的过程，称为“正向传播”，这个是需要我们自己动手的，因为我们需要设计我们模型的结构。由损失函数求导的过程，称为“反向传播”，求导是件辛苦事儿，所以自动求导基本上是各种深度学习框架的基本功能和最重要的功能之一，PyTorch也不例外。

一、pytorch自动求导初步认识

比如有一个函数，y=x的平方（y=x2）,在x=3的时候它的导数为6，我们通过代码来演示这样一个过程。

x=torch.tensor(3.0,requires_grad=True)
y=torch.pow(x,2)

#判断x,y是否是可以求导的
print(x.requires_grad)
print(y.requires_grad)

#求导，通过backward函数来实现
y.backward()

#查看导数，也即所谓的梯度
print(x.grad)

最终的运行结果为：

True
True
tensor(6.) #这和我们自己算的是一模一样的。

这里有一些关键点

1.1 tensor的创建与属性设置

先来看一下tensor的定义：

tensor(data, dtype=None, device=None, requires_grad=False) -> Tensor

参数:
data： (array_like): tensor的初始值. 可以是列表，元组，numpy数组，标量等;
dtype： tensor元素的数据类型
device： 指定CPU或者是GPU设备，默认是None
requires_grad：是否可以求导，即求梯度，默认是False，即不可导的

（1）tensor对象的requires_grad属性

每一个tensor都有一个requires_grad属性，表示这个tensor是否是可求导的，如果是true则可以求导，否则不能求导，语法格式为：

x.requires_grad 判断一个tensor是否可以求导，返回布尔值

需要注意的是，只有当所有的“叶子变量”，即所谓的leaf variable都是不可求导的，那函数y才是不能求导的，什么是leaf variable呢？这其实涉及到“计算图”相关的知识，但是我们通过下面的例子一下就能明白了，如下：

#创建一个二元函数，即z=f(x,y)=x2+y2，x可求导，y设置不可求导
x=torch.tensor(3.0,requires_grad=True)
y=torch.tensor(4.0,requires_grad=False)
z=torch.pow(x,2)+torch.pow(y,2)

#判断x,y是否是可以求导的
print(x.requires_grad)
print(y.requires_grad)
print(z.requires_grad)

#求导，通过backward函数来实现
z.backward()

#查看导数，也即所谓的梯度
print(x.grad)
print(y.grad)

运行结果为：

True # x是可导的
False # y是不可导的
True # z是可导的，因为它有一个 leaf variable 是可导的，即x可导
tensor(6.) # x的导数
None # 因为y不可导，所以是none

如果是上面的 leaf variable变量x也设置为不可导的，那么z也不可导，因为x、y均不可导，那么z自然不可导了。

（2）leaf variable（也是tensor）的requires_grad_()方法

如果某一个叶子变量，开始时不可导的，后面想设置它可导，或者反过来，该怎么办呢？tensor提供了一个方法，即

x.requires_grad_(True/False) 设置tensor的可导与不可导，注意后面有一个下划线哦！

但是需要注意的是，我只能够设置叶子变量，即leaf variable的这个方法，否则会出现以下错误：

RuntimeError: you can only change requires_grad flags of leaf variables.

1.2 函数的求导方法——y.backward()方法

上面只演示了简单函数的求导法则，

需要注意的是：如果出现了复合函数，比如 y是x的函数，z是y的函数，f是z的函数，那么在求导的时候，会使用 f.backwrad()只会默认求f对于叶子变量leaf variable的导数值，而对于中间变量y、z的导数值是不知道的，直接通过x.grad是知道的、y.grad、z.grad的值为none。

下面来看一下这个函数backward的定义：

backward(gradient=None, retain_graph=None, create_graph=False)

它的三个参数都是可选的，上面的示例中还没有用到任何一个参数，关于这三个参数，我后面会详细说到，这里先跳过。

1.3 查看求得的导数的值——x.grad属性

通过tensor的grad属性查看所求得的梯度值。

总结：

（1）torch.tensor()设置requires_grad关键字参数

（2）查看tensor是否可导，x.requires_grad 属性

（3）设置叶子变量 leaf variable的可导性，x.requires_grad_()方法

（4）自动求导方法 y.backward() ，直接调用backward()方法，只会计算对计算图叶节点的导数。

（5）查看求得的到数值， x.grad 属性

易错点：

为什么上面的标量x的值是3.0和4.0，而不是整数呢？这是因为，要想使x支持求导，必须让x为浮点类型，也就是我们给初始值的时候要加个点：“.”。不然的话，就会报错。 即，不能定义[1,2,3]，而应该定义成[1.,2.,3.]，前者是整数，后者才是浮点数，浮点数才能求导。

二、求导的核心函数——backwrad函数详解

2.1 默认的求导规则

在pytorch里面，默认：只能是【标量】对【标量】，或者【标量】对向【量/矩阵】求导！这个很关键，很重要！

（1）标量对标量求导

参见上面的例子，x,y,z都是标量，所以求导过程也很简单，不再赘述。

（2）标量对向量/矩阵求导

为什么标量对于向量/矩阵是默认的呢？因为在深度学习中，我们一般在求导的时候是对损失函数求导，损失函数一般都是一个标量，即将所有项的损失加起来，但是参数又往往是向量或者是矩阵，所以这就是默认的了。看下面的例子。

比如有一个输入层为3节点的输入层，输出层为一个节点的输出层，这样一个简单的神经网络，针对以组样本而言，有

X=（x1,x2,x3）=(1.5,2.5,3.5)，X是（1,3）维的，输出层的权值矩阵为W=（w1,w2,w3）T=(0.2,0.4,0.6)T，这里表示初始化的权值矩阵，T表示转置，则W表示的是（3,1）维度，偏置项为b=0.1,是一个标量，则可以构建一个模型如下：

Y=XW+b，其中W,b就是要求倒数的变量，这里Y是一个标量，W是向量，b是标量，W,b是叶节点，leaf variable，

将上面展开得到：

Y=x1w1+x2w2x3w3+b （这里的1,2,3是下标，不是次方哦！难得用公式截图）

自己手动计算得到，

Y对w1的导数为1.5

Y对w2的导数为2.5

Y对w3的导数为3.5

Y对b的导数为1

下面我们来验证一下：

#创建一个多元函数，即Y=XW+b=Y=x1*w1+x2*w2*x3*w3+b，x不可求导，W,b设置可求导
X=torch.tensor([1.5,2.5,3.5],requires_grad=False)
W=torch.tensor([0.2,0.4,0.6],requires_grad=True)
b=torch.tensor(0.1,requires_grad=True)
Y=torch.add(torch.dot(X,W),b)


#判断每个tensor是否是可以求导的
print(X.requires_grad)
print(W.requires_grad)
print(b.requires_grad)
print(Y.requires_grad)


#求导，通过backward函数来实现
Y.backward()

#查看导数，也即所谓的梯度
print(W.grad)
print(b.grad)

运行结果为：

False
True
True
True
tensor([1.5000, 2.5000, 3.5000])
tensor(1.)

我们发现这和我们自己算的结果是一样的。

（3）标量对向量/矩阵求导的进一步理解

比如有下面的一个复合函数，而且是矩阵，定义如下：

x 是一个（2,3）的矩阵，设置为可导，是叶节点，即leaf variable
y 是中间变量,由于x可导，所以y可导
z 是中间变量,由于x，y可导，所以z可导
f 是一个求和函数，最终得到的是一个标量scaler

x = torch.tensor([[1.,2.,3.],[4.,5.,6.]],requires_grad=True)
y = torch.add(x,1)
z = 2*torch.pow(y,2)
f = torch.mean(z)

则x,y,z,f实际上的函数关系如下：

$$X=\left[\begin{array}{ccc}{X}_{11}& X_{12}& X_{13}\\ X_{21}& X_{22}& X_{23}\end{array}\right]$$

$$\mathrm{y}=\left[\begin{array}{lll}{y}_{11}& y_{12}& y_{13}\\ y_{21}& y_{22}& y_{23}\end{array}\right]$$

$$\mathrm{Z}=\left[\begin{array}{lll}{Z}_{11}& Z_{12}& Z_{13}\\ Z_{21}& Z_{22}& Z_{23}\end{array}\right]$$

$f$为：

$$\begin{array}{rl}& f=\frac{{\sum }_{i=1}^6{z}_i}{6}=\frac{z_{11}+z_{12}+z_{13}+z_{21}+z_{22}+z_{23}}{6}\\ =& \frac{2\left({\mathrm{y}}_{11}^2+{\mathrm{y}}_{12}^2+{\mathrm{y}}_{13}^2+{\mathrm{y}}_{21}^2+{\mathrm{y}}_{22}^2+{\mathrm{y}}_{23}^2\right)}{6}\\ =& \frac{2\left[{\left(x_{11}+1\right)}^2+{\left(x_{12}+1\right)}^2+{\left(x_{13}+1\right)}^2+{\left(x_{21}+1\right)}^2+{\left(x_{22}+1\right)}^2+{\left(x_{23}+1\right)}^2\right]}{6}\end{array}$$

可见现在我么自己都可以手动求出函数f对于x11,x12,x13,x21,x22,x23的导数了，那我们通过torch来试一试。

print(x.requires_grad)
print(y.requires_grad)
print(z.requires_grad)
print(f.requires_grad)
print('===================================')
f.backward()
print(x.grad)

运行结果为：

True
True
True
True
===================================
tensor([[1.3333, 2.0000, 2.6667],
[3.3333, 4.0000, 4.6667]])

现在我们是不是更加了解自动求导的规则了呢？

标量如何对标量、向量、矩阵求导数！！！

2.2 向量/矩阵 对 向量/矩阵求导——通过backward的第一个参数gradient来实现

（1）求导的一个规则

比如有下面的例子：

x 是一个（2,3）的矩阵，设置为可导，是叶节点，即leaf variable
y 也是一个（2,3）的矩阵，即
y=x2+x (x的平方加x)
实际上，就是要y的各个元素对相对应的x求导

x = torch.tensor([[1.,2.,3.],[4.,5.,6.]],requires_grad=True)
y = torch.add(torch.pow(x,2),x)

gradient=torch.tensor([[1.0,1.0,1.0],[1.0,1.0,1.0]])

y.backward(gradient)

print(x.grad)

运行结果为：

tensor([[ 3., 5., 7.],
[ 9., 11., 13.]])

这其实跟我们自己算的是一样的，

相较于上面的标量对于向量或者是矩阵求导，关键是backward（）函数的第一个参数gradient，那么这个参数是什么意思呢？

为了搞清楚传入的这个gradient参数到底做了什么工作，我们进一步做一个实验，有下面的一个向量对向量的求导，即

x = torch.tensor([1.,2.,3.],requires_grad=True)
y = torch.pow(x,2)

gradient=torch.tensor([1.0,1.0,1.0])
y.backward(gradient)
print(x.grad)

得到的结果：

tensor([2., 4., 6.]) 这和我们期望的是一样的

因为这里的gradient参数全部是1，所以看不出差别，现在更改一下gradient的值，如下：

gradient=torch.tensor([1.0,0.1,0.01])

输出为：

tensor([2.0000, 0.4000, 0.0600])

从结果上来看，就是第二个导数缩小了十倍，第三个导数缩小了100倍，这个倍数和gradient里面的数字是息息相关的。

如果你想让不同的分量有不同的权重，从效果上来理解确实是这样子的，比如我是三个loss，loss1，loss2，loss3，它们的权重可能是不一样的，我们就可以通过它来设置，即

dy/dx=0.1*dy1/dx+1.0*dy2/dx+0.0001*dy3/dx。

需要注意的是，gradient的维度是和最终的需要求导的那个y的维度是一样的，从上面的两个例子也可以看出来。

总结：gradient参数的维度与最终的函数y保持一样的形状，每一个元素表示当前这个元素所对应的权重

2.3 自动求导函数backward的第二、第三个参数

（1）保留运算图——retain_graph

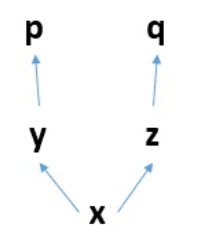
在构建函数关系的时候，特别是多个复合函数的时候，会有一个运算图，比如下面：

则有如下一些函数关系：

p=f(y)——>y=f(x)

q=f(z)——>z=f(x)

一个计算图在进行反向求导之后，为了节省内存，这个计算图就销毁了。 如果你想再次求导，就会报错。

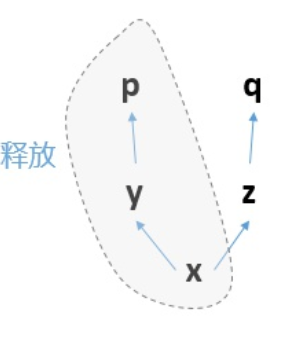
就比如这里的例子而言，

你先求p求导，那么这个过程就是反向的p对y求导，y对x求导。 求导完毕之后，这三个节点构成的计算子图就会被释放：

那么计算图就只剩下z、q了，已经不完整，无法求导了。 所以这个时候，无论你是想再次运行p.backward()还是q.backward()，都无法进行，因为x已经被销毁了，报错如下：

RuntimeError: Trying to backward through the graph a second time, but the buffers have already been freed. Specify retain_graph=True when calling backward the first time.

那怎么办呢？遇到这种问题，我们可以通过设置 retain_graph=True 来保留计算图，

即更改你的backward函数，添加参数retain_graph=True，重新进行backward，这个时候你的计算图就被保留了，不会报错。 但是这样会吃内存！，尤其是，你在大量迭代进行参数更新的时候，很快就会内存不足，所以这个参数在绝大部分情况下是不要去使用的。

（2）高阶导数——create_graph

create_graph参数的资料现在很少，我也还没有搜寻到一些更详细的用法，它的官方描述是这样的：

更高层次的计算图会创建出来，允许计算高阶导数，如二阶导数、三阶导数等等，下面有一个简单的小例子：

x = torch.tensor(5.0,requires_grad=True)
y = torch.pow(x,3)

grad_x = torch.autograd.grad(y, x, create_graph=True)
print(grad_x) # dy/dx = 3 * x^2，即75

grad_grad_x = torch.autograd.grad(grad_x[0],x)
print(grad_grad_x) # 二阶导数 d(2x)/dx = 30

运行结果为：

(tensor(75., grad_fn=<MulBackward0>),)
(tensor(30.),)

三、关于向量对向量求导的解释

补充说明：关于向量对向量求梯度的进一步绕论：

比如说下面一个三维向量求梯度：

然后，要计算z关于x或者y的梯度，需要将一个外部梯度传递给z.backward()函数，如下所示：

z.backward(torch.FloatTensor([1.0, 1.0, 1.0])

反向函数传递的张量就像梯度加权输出的权值。从数学上讲，这是一个向量乘以非标量张量的雅可比矩阵(本文将进一步讨论)，因此它几乎总是一个维度的单位张量，与 backward张量相同，除非需要计算加权输出。

注意 ：向后图是由autograd类在向前传递过程中自动动态创建的。Backward()只是通过将其参数传递给已经生成的反向图来计算梯度。

数学—雅克比矩阵和向量

从数学上讲，autograd类只是一个雅可比向量积计算引擎。雅可比矩阵是一个非常简单的单词，它表示两个向量所有可能的偏导数。它是一个向量相对于另一个向量的梯度。

注意：在这个过程中，PyTorch从不显式地构造整个雅可比矩阵。直接计算JVP (Jacobian vector product)通常更简单、更有效。

如果一个向量X = [x1, x2，…xn]通过f(X) = [f1, f2，…fn]来计算其他向量，则雅可比矩阵(J)包含以下所有偏导组合：
$$\mathbf{J}=\left[\begin{array}{ccc}\frac{\partial \mathbf{f}}{\partial x_1}& \cdots & \frac{\partial \mathbf{f}}{\partial x_n}\end{array}\right]=\left[\begin{array}{ccc}\frac{\partial f_1}{\partial x_1}& \cdots & \frac{\partial f_1}{\partial x_n}\\ ⋮& \ddots & ⋮\\ \frac{\partial f_m}{\partial x_1}& & \frac{\partial f_m}{\partial x_n}\end{array}\right]$$

注意：雅可比矩阵实现的是 n维向量 到 m 维向量的映射。

雅克比矩阵

上面的矩阵表示f(X)相对于X的梯度。

假设一个启用PyTorch梯度的张量X：

X = x1,x2,…,xn

X经过一些运算形成一个向量Y

Y = f(X) = [y1, y2，…,ym]

然后使用Y计算标量损失l。假设向量v恰好是标量损失l关于向量Y的梯度，如下：（注意体会这句话，这个很重要！）
$$v={\left(\frac{\partial l}{\partial y_1}\cdots \frac{\partial l}{{\partial }_{y_i}}\right)}^T$$

向量v称为grad_tensor（梯度张量），并作为参数传递给backward() 函数。

为了得到损失的梯度l关于权重X的梯度，雅可比矩阵J是向量乘以向量v

$$J\cdot v=\left(\begin{array}{ccc}\frac{\partial y_1}{\partial x_1}& \cdots & \frac{\partial y_m}{\partial x_1}\\ ⋮& \ddots & ⋮\\ \frac{\partial y_1}{\partial x_n}& \cdots & \frac{\partial y_m}{\partial x_n}\end{array}\right)\left(\begin{array}{c}\frac{\partial l}{\partial y_1}\\ ⋮\\ \frac{\partial l}{\partial y_m}\end{array}\right)=\left(\begin{array}{c}\frac{\partial l}{\partial x_1}\\ ⋮\\ \frac{\partial l}{\partial e_j}\end{array}\right)$$
这种计算雅可比矩阵并将其与向量v相乘的方法使PyTorch能够轻松地为非标量输出提供外部梯度。

四、求导的另外两种方法

方法一：通过 torch.autograd.backward(）求导

前面介绍的求导的基本公式为：

y.backward(grad_tensors=None, retain_graph=None, create_graph=False),这三个参数我在前面已经说了，

反向求导它等价于：

torch.autograd.backward(tensors,grad_tensors=None, retain_graph=None, create_graph=False), 这里的tensors参数就相当于是y,

所以：

y.backward(） #标量y 等价于

torch.autograd.backward(y)。

需要注意的是，这个函数只是提供求导功能，并不返回值，返回的总是None，如下例子：

import torch

x=torch.tensor([1.0,2.0,3.0],requires_grad=True)
y=torch.tensor([4.0,5.0,6.0],requires_grad=True)

z=torch.sum(torch.pow(x,2)+torch.pow(y,3)) # z=x2+y3

torch.autograd.backward([z]) # 求导，等价于z.backward()

print(x.grad) # 获取求导的结果
print(y.grad)

输出

tensor([2., 4., 6.])
tensor([ 48., 75., 108.])

注意事项：

（1）该方法只负责求导，返回的总是None，

（2）当向量对向量求导的时候，需要传递参数grad_tensor，这个参数的含义其实和前一篇文章的y.backward()里面的那个是一个含义；

（3）retain_graph=None, create_graph=False 也和前面的含义是一样的

方法二：通过torch.autograd.grad(）来求导

除了前面的两种方法来求导以外，即

y.backward()

torch.autograd.backward(y) 这两种方法

还有一种方法，即通过torch.autograd.grad(）来求导，先来看一下这个函数的定义。

def grad(outputs, inputs, grad_outputs=None, retain_graph=None, create_graph=False,only_inputs=True, allow_unused=False):

outputs : 函数的因变量，即需要求导的那个函数，在本例子中，为z，当然，他可以是一个tensor，也可以是几个tensor，如[tensor1,tensor2,tensor3…]
inputs : 函数的自变量，在本例中，即对应的是[x,y]，他可以是一个tensor，也可以是几个tensor，如[tensor1,tensor2,tensor3…]
grad_output : 这个参数和前面两种方法中的grad_tensors是同样的含义，当出现向量对向量求导的时候需要指定该参数

依然以这个例子而言，来看一下怎么做：

import torch

x=torch.tensor([1.0,2.0,3.0],requires_grad=True)
y=torch.tensor([4.0,5.0,6.0],requires_grad=True)

z=torch.sum(torch.pow(x,2)+torch.pow(y,3)) # z=x2+y3

print(torch.autograd.grad(z,[x,y])) # 求导，并且返回值

输出

(tensor([2., 4., 6.]), tensor([ 48., 75., 108.]))

注意事项：

该函数会自动完成求导过程，而且会自动返回对于每一个自变量求导的结果。这是和前面不一样的地方。

参考自：沈鹏燕