Problem: 28. 找出字符串中第一个匹配项的下标
kmp算法,超清晰多图逐步图解!
kmp算法的核心在next数组,因此如果能够理解next数组的求解过程,就会发现子串和主串的匹配过程,是和求next数组的过程是完全一致的。
因此我们这里先讲解next数组的求解过程。
先不考虑kmp算法中next数组的作用,先从简单的概念入手,next数组是有它本身的含义的:就是字符串的最长公共前后缀的大小。
我们从最长公共前后缀的大小这个定义出发,来求解next数组,并逐渐理解kmp算法的核心思想。
最长公共前后缀
前缀
前缀的概念:字符串起始部分(不能是整个字符串)
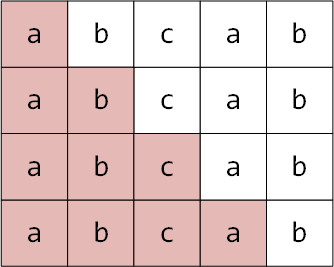
对于字符串"abcab",它有"a" "ab" "abc" "abca" 这样四个前缀
前缀的最大长度不能等于整个字符串的长度,比如示例中"abcab"的最长前缀是abca,而不能是整个字符串"abcab"
后缀
后缀的概念:字符串末尾部分(不能是整个字符串)
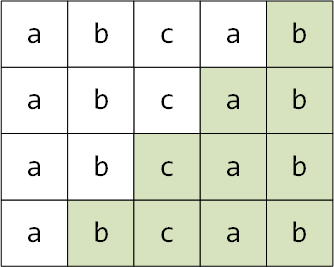
同样,对于字符串"abcab",它有"b" "ab" "cab" "bcab" 这样四个后缀
同样,后缀的最大长度不能等于整个字符串的长度,比如示例中"abcab"的最长后缀是bcab,而不能是整个字符串"abcab"
最长公共前后缀(的长度)
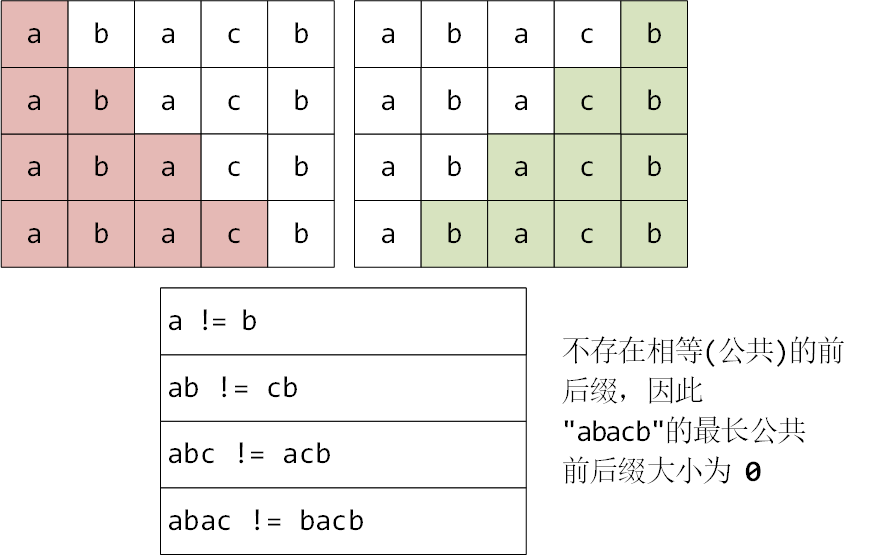
最长公共前后缀的定义是:按照前后缀的长度,从小到大比较,从各组相等的前后缀中,返回长度最大的一组前后缀的长度。
如果字符串中不存在任一组前后缀相等,那么该字符串最长公共前后缀的长度就是0。(公共的意思,指的就是前后缀相等。)
举例:
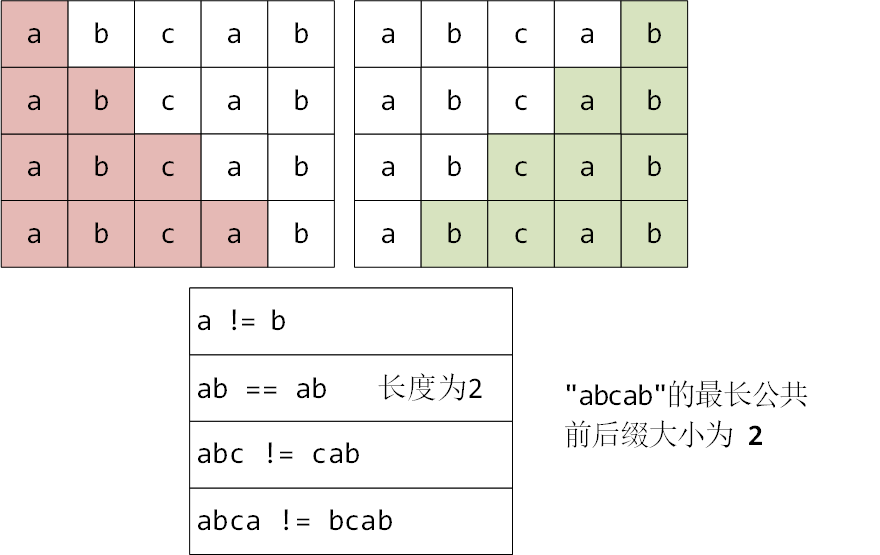
对于字符串"abcab",求最长公共前后缀长度的过程如下
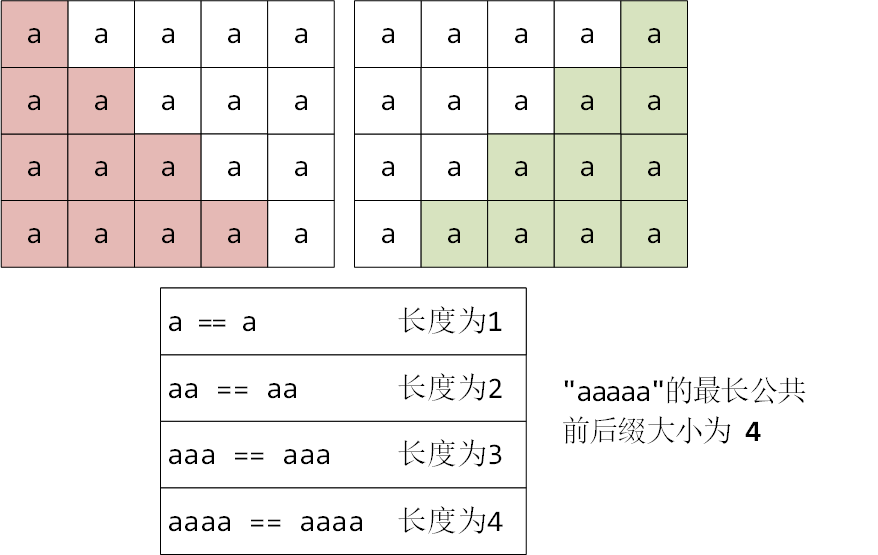
对于字符串"aaaaa",求最长公共前后缀长度的过程如下
对于字符串"aaaab",求最长公共前后缀长度的过程如下
对于字符串"abacb",求最长公共前后缀长度的过程如下
特殊情况1:对于只包含一个字符的字符串"a",求其最长公共前后缀的长度:
根据之前的概念,前后缀不能是整个字符串,因此对于只包含一个字符的字符串比如 "a",是不存在前后缀的,因此其最长公共前后缀长度为0。
特殊情况2:同理,对于空字符串”“, 也是不存在前后缀的,因此空字符串的最长公共前后缀长度也记为0。
这里我们发现,求解一个字符串的最长公共前后缀 ,默认使用的是暴力迭代的方法。
我们实际上是按照前后缀的长度,从1 ~ n - 1,逐个遍历每个长度,比较前后缀是否相等,然后返回相等的前后缀中,长度最大的那个。
next数组
理解了最长公共前后缀的定义之后,我们可利用最长公共前后缀,来给出next数组的定义
对于任意一个字符串p,其长度为
n
\rm n
n,p对应的next数组记为 next[n],则next数组定义如下
n
e
x
t
[
j
]
=
{
子串
p
[
0
,
.
.
,
j
−
1
]
的最长公共前后缀长度
;
}
0
≤
j
≤
n
\rm next[j] = \{子串p[0,..,j - 1]的最长公共前后缀长度;\}\ \ \ \ \ 0\le j \le n
next[j]={子串p[0,..,j−1]的最长公共前后缀长度;} 0≤j≤n
O(n^2) 求法
我们完全可以使用之前的暴力方法,遍历p的每一个子串,再对每个子串遍历所有长度的前后缀,这就是暴力求解next数组的方法
(可以提交通过,不超时)。
// 求解字符串p的 next数组
void get_next(vector<int>& next, string p)
{
int n = p.size();
next.assign(n + 1, 0);
next[0] = 0, next[1] = 0; // 1.子串为空 2.子串只包含一个字符。两个特殊情况;
for(int j = 2; j <= n; j++) // 遍历p的所有子串
{
string tmp = p.substr(0, j); // p的子串
// 因为求的是最大公共前后缀,因此让前后缀长度从大到小遍历,
// 这样找到的第一个相等的前后缀的长度len,就是next[j]的值
for(int len = j - 1; len >= 1; len--)
if(tmp.substr(0, len) == tmp.substr(j - len, len)) // 比较p的子串的前后缀是否相等
{
next[j] = len;
break;
}
}
}
下面四个例子,可以从直观上看出next数组的求解过程
字符串 "abcab" 的 next 数组求解过程
字符串 "aaaaa" 的 next 数组求解过程
字符串 "aaaab" 的 next 数组求解过程
字符串 "abacb" 的 next 数组求解过程
可以发现只要字符串p不为空,那么p的next[0] next[1] 分别表示空串和长度为1的字符串的最长公共前后缀,这两个值恒为0。
因此可以从j = 2开始求next[j]。
O(n) 求法
next数组的暴力求法复杂度为 O ( n 2 ) \rm O(n^2) O(n2)。
能不能只遍历一次j,也就是使用
O
(
n
)
\rm O(n)
O(n)的复杂度,就把next数组求出来呢?
答案是可以的,这也正是kmp算法的核心。
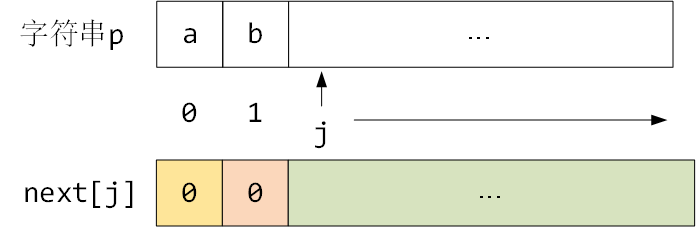
如下图所示,随着j的遍历,如果每遍历到一个j,就能求得next[j]的值,遍历完毕的时候,整个next数组就被求出来了。
这样就是一个 O ( n ) \rm O(n) O(n) 的复杂度了
具体该如何求呢?我们考虑一个一般的情况:
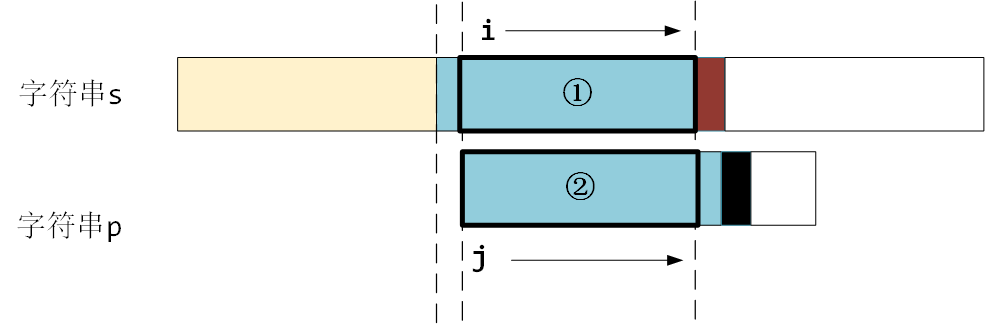
假设当前j遍历到了如下图所示的位置,并且当前的 next[j] 已经求出来,将当前的 next[j] 的值记为 i。
根据next数组的定义,next[j] 也就是 i 表示的是 p[0,...j-1]的最长公共前后缀的长度,也就是 ① 和 ② 相等,并且长度为 i。
(1)初始状态:如下图所示,当前的 next[j]记为 i,两个浅蓝色区域 ① 和 ② 分别表示前缀和后缀部分
(2)求下一个位置的 next[j] 值
如图所示,j++,j移动到下一个位置
我们就可以利用上一个子串的next值来求,也就是利用 next[j - 1] 的值来求。
next[j] 表示的是 子串 p[0,...j-1]的最长公共前后缀长度
next[j - 1]表示的是 子串 p[0,...j-2]的最长公共前后缀长度
next[j - 1] 的值为 i,说明上图中长度为 i 的蓝色区域是相等的(最长公共前后缀),因此如果p[i] 和 p[j - 1] 也相等的话,
那么 ① + p[i] 和 ② + p[j - 1] 就组成了当前子串的最长公共前后缀。
我们只需要判断,p[i] 和 p[j - 1] 是否相等。
如果相等,那么相当于当前子串的最长公共前后缀,相比前一个子串的最长公共前后缀,多加了 1,也就是
next[j] = i + 1; 如下图所示。
如果p[i] 和 p[j - 1] 不相等
p[i] 和 p[j - 1] 不相等,那么 ① + p[i] 和 ② + p[j - 1] 就必不可能相等,这两部分也就无法构成最长公共前后缀了。
那我们需要找一个新的最长的公共前后缀的位置 i',该如何找呢?
如上图所示,我们试图在 ① 中找一个最长的前缀 ③ ,然后在 ② 中找一个相等的最长的后缀 ④ 。
然后,试图将 ③ + p[i'] 和 ④ + p[j - 1] 匹配,看看能否组成最长的公共前后缀。
我们发现一个问题: ① 和 ② 本身就构成了最长公共前后缀,因此 ① == ②,二者是相等的。
因此
在 ① 中找一个最长的前缀 ③ ,然后在 ② 中找一个相等的最长的后缀 ④,
等价于
在 ① (或②)中同时找一个最长的前缀 ③,和一个 相等的最长的后缀 ④
如下图所示。
这不正是子串 ① 的最长公共前后缀的定义吗?
子串 ① 的最长公共前后缀的值正是 next[i],i 的值比 j 小,因此遍历到 j 的时候 next[i]的值已知。
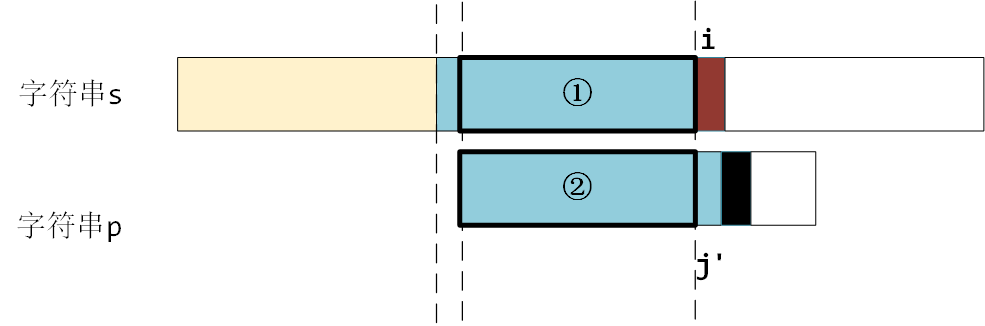
所以说我们要找的位置 i',正是 next[i],也就是 i = next[i],如下图所示
令 i = next[i],如果p[i] == p[j - 1]
那么 ③ + p[i] 和 ④ + p[j - 1] 就构成了子串 p[0,...j-1] 的最长公共前后缀,长度 next[j] = i + 1;(注意这里已经是新的 i 了)
如果p[i] 和 p[j - 1] 仍然不相等,就重复上面的过程就好了。
如果一直匹配失败,最终 i 会等于0,也就是停到字符串首部 p[0]的位置。
此方法复杂度为 O ( n ) \rm O(n) O(n),上述过程求next数组的代码如下。
void get_next(vector<int>& next, string p)
{
int n = p.size();
next[0] = 0, next[1] = 0;
for(int j = 2, i = 0; j <= n; j++)
{
if(i > 0 && p[i] != p[j - 1]) i = next[i];
if(p[i] == p[j - 1]) i++;
next[j] = i;
}
}
子串和主串匹配的过程
回到kmp算法。kmp算法求的是:子串 p 在 主串 s 中出现的位置。
分析子串和主串的匹配过程,考虑一般的情况:
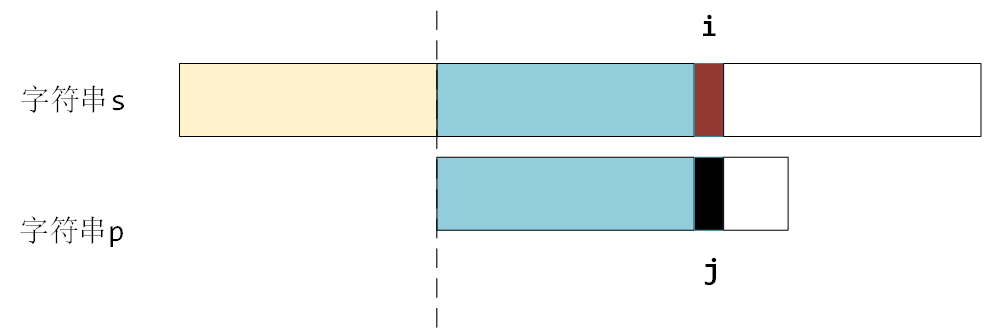
如图所示,假设匹配到这个位置的时候,匹配失败了
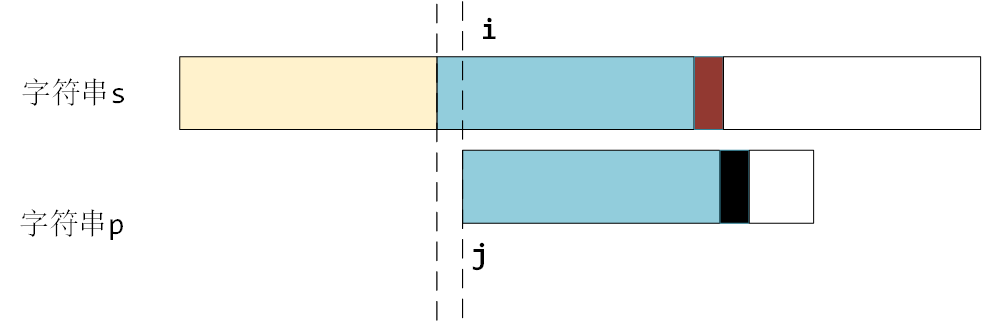
如果按照暴力解法的话,需要 j 回到起始位置,i 也要回退到之前匹配的下一个位置,重新逐个开始匹配,如图所示
暴力做法最不合理的地方在于:如下图所示,如果 ① 和 ② 本来就是不相等的,那么 i 和 j 这样逐渐匹配是徒劳的,因为子串的前部分 ② 已经和主串的 ① 匹配不上了,即使之后的匹配完全相等,最终结果也不会相等。
那么如果 ① 和 ② 相等呢? 如果能够提前知道 ① 和 ② 相等的话,也不需要逐个匹配了,因为逐个匹配成功后的结果 i 仍回到了原来的位置,综上, i的位置是可以不动的,只需要调整子串 j 的位置即可。如下图所示
那么如何调整 j 的值呢?有两个要求。
1.首先 ① 和 ② 必须相等,我们发现整个蓝色部分是刚刚匹配成功的部分,所以 ① 是蓝色区域的后缀,② 是蓝色区域的前缀,也就是找出字符串p的蓝色区域子串中,相等的前后缀。
2.这个相等的前后缀必须是最长的。假设不是最长的话,如果存在更长的前后缀,却没有进行匹配,这样就会遗漏可能匹配的情况。并且最长的相等前后缀,保证了比它还长的前后缀,不可能再有相等(匹配上)的情况了,因为其本身已经是最长的相等前后缀了。因此每次子串必须调整 j 的位置到最长的相等的前后缀的位置。
可以发现,这正是之前所求的最长公共前后缀(也就是next数组)的概念。
主串子串匹配过程的代码如下
vector<int> kmp(string s, string p, vector<int>& next)
{
vector<int> res; // 保存 p 在 s 中出现的位置的索引
for(int i = 0, j = 0; i < s.size(); i++)
{
while(j > 0 && s[i] != p[j]) j = next[j]; // 匹配失败 调整 j 的位置
if(s[i] == p[j]) j++; // 匹配成功 j++ 继续匹配
if(j == p.size()) // j到了子串p末尾,说明 完全匹配到了一个答案,记录结果,然后继续调整j寻找
{
res.push_back(i - j + 1);
j = next[j];
}
}
return res;
}
补充
1.实际上, next[0] 的值根本不会用到,取多少都可以
因为 p[0] 匹配失败的话,也就是第一个字符就匹配失败了,此时 i++ ,那么字符串p整体前移,从字符串s的下一个位置开始匹配,j 仍保持在 p[0] 的位置,继续匹配。
2.对next数组优化
如果我们跳转到的位置的字符,和当前字符相同的话,就没必要比较了。
因为当前字符匹配失败,再用一个相同的字符去匹配,肯定还是失败。
void get_next(string p, vector<int>& next)
{
int n = p.size();
next.assign(n + 1, 0);
next[0] = next[1] = 0;
for(int j = 2, i = 0; j <= n; j++)
{
while(i > 0 && p[j - 1] != p[i]) i = next[i];
if(p[j - 1] == p[i]) i++;
next[j] = i;
/* 增加下面这两行代码 */
if(p[next[j]] == p[j])
next[j] = next[next[j]];
}
}