一、最小二乘法的引出

我们考虑下面一个方程组的求解：
$$\begin{gathered} x_1+x_2=5 \\ {x}_1-x_2=3 \\ {x}_1+x_2=4 \end{gathered}$$
可以写成形如$Ax=b$的矩阵形式：
$$\left[\begin{array}{cc}1& 1\\ 1& -1\\ 1& 1\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=\left[\begin{array}{c}5\\ 3\\ 4\end{array}\right]$$
由线性代数的知识可知，当方程个数m大于未知两个数n的时候，方程通常无解。但是对于$Ax=b$这个方程而言，我们仍然可以通过一些方法得到一个最接近解析解的一个向量，这个方法就是最小二乘法。
最小二乘法的抽象形式如下所示：
$$目标函数=\sum (观测值-理论值{)}^2$$
观测值指的就是我们的多组样本，而理论值就是我们假设的拟合函数。目标函数就是我们常说的损失函数。我们的目标是得到使目标函最小化时的拟合函数模型。

我们举一个简单的例子，假设有m个测试样本：$(x_i,y_i)(i=1,2,3,......m)$，我们需要找到一个n维的变量$x^{\ast }\in \mathbb{R}$,使得损失函数$F(x)$取得局部最小值：
$$F(x)=\frac{1}{2}\sum _{i=1}^m(f_i(x){)}^2$$
其中$f_i$是残差函数，即测量值和预测值之间的差，且有$m>n$。而局部最小值指任意的$||x-x^{\ast }||<\delta$ 有$F(x^{\ast })\le F(x)$。

二、线性最小二乘法

1.线性最小二乘的描述

对于$m$个方程求解$n$个未知数，有三种情况：

• $m=n$且A为非奇异，则有唯一解，$x=A^{-1}b$
• 当$m>n$，约束的个数大于未知数的个数，称为超定方程（overdetermined）
• $m<n$，负定/欠定问题(underdetermind)

通常我们遇到的问题都是超定问题，此时$Ax=b$的解是不存在的，从而转向解最小二乘问题：
$$J(x)=min||Ax-b|{|}_2^2$$
$J(x)$为凸函数，我们令一阶导数为0，可以得到：
$$x=(A^{T}A{)}^{(-1)}{A}^{T}b$$

2.线性最小二乘特殊情况的求解

这时候我们考虑齐次方程$Ax=0$，当A行数大于列数的特殊情况：
$$min||Ax||$$
此时的最小二乘解为$A^{T}A$最小特征值对应的特征向量。我们可以通过以下方式进行求解；

3.线性最小二乘一般情况的求解

对于一个线性方程求解问题而言，最简单粗暴的方式是对$A^{T}A$求逆，但是这种方式计算量极大，非常耗时，所以我们考虑用矩阵分解的方式加速线性最小二乘问题的求解。

矩阵分解是将矩阵拆解为数个矩阵的乘积，可分为三角分解、满秩分解、QR分解、Jordan分解、SVD（奇异值）分解等，常见的有三种：1)QR 分解法，2)Cholesky分解法，3)SVD分解法

1. LU三角分解：三角分解法是将原正方 (square) 矩阵分解成一个上三角形矩阵和一个下三角形矩阵.
2. QR分解：QR分解法是将矩阵分解成一个正规正交矩阵与上三角形矩阵,所以称为QR分解法。
3. 奇异值分解：[U,S,V]=svd(A)，其中U和V分别代表两个正交矩阵，而S代表一对角矩阵。SVD是最可靠的分解法，但是它比QR 分解法更加耗时。
4. LLT分解：Cholesky 分解是把一个对称正定的矩阵表示成一个下三角矩阵L和其转置的乘积的分解。它要求矩阵的所有特征值必须大于零，故分解的下三角的对角元也是大于零的（LU三角分解法的变形）。
5. LDLT分解法：其中L为下三角形单位矩阵，D为对角矩阵，L^T为L的转置矩阵。LDLT分解法实际上是Cholesky分解法的改进，因为Cholesky分解法虽然不需要选主元，但其运算过程中涉及到开方问题，而LDLT分解法则避免了这一问题。

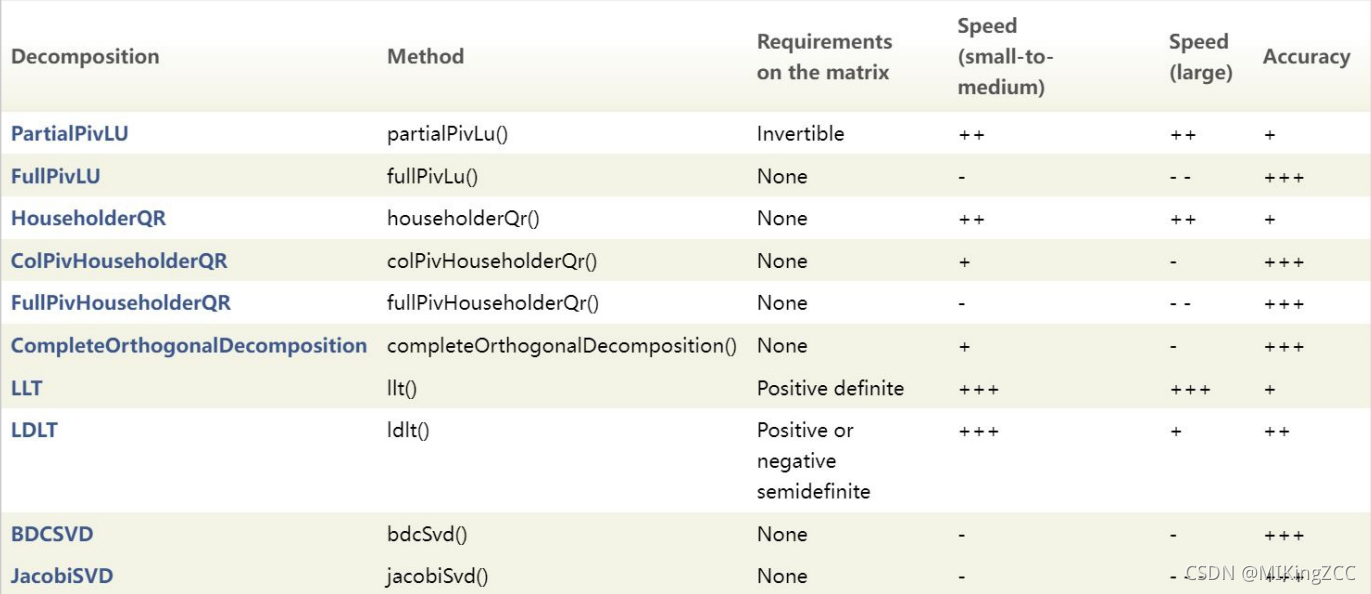
以下是eigen库中提供的矩阵分解求解线性最小二乘问题的方法，我们可以根据实际需求做出选择。

三、非线性最小二乘法

1.非线性最小二乘的描述

考虑一个非线性最小二乘模型如下：
$$F(x)=\frac{1}{2}\sum _{i=1}^m(f_i(x){)}^2$$
我们假设损失函数$F(x)$是平滑可导的，所以我们在二阶泰勒展开有：
$$F(x+\Delta x)=F(x)+J\Delta x+\frac{1}{2}\Delta x^{T}H\Delta x+O(||\Delta |{|}^3)$$
其中$J$和$H$分别为损失函数$F$对变量$x$的一阶导和二阶导矩阵。

2.非线性最小二乘的求解

我们求解的思路是寻找一个下降方向使损失函数随$x$的迭代逐渐减小，直到$x$收敛到$x^{\ast }$时有:
$$F(x^{\ast })\le F(x)x\in \forall$$
所以我们需要寻找下降方向的单位向量$d$和下降步长$\alpha$。假设我们的$\alpha$足够小，我们对损失函数$F(x)$进行一阶泰勒展开：
$$F(x+\alpha d)\approx F(x)+\alpha Jd$$
我们的下降方向只要满足：
$$Jd<0$$
而下降的步长可以通过线性搜索的方式寻找：
$${\alpha }^{\ast }=argmi{n}_{\alpha >0}F(x+\alpha d)$$

a. 最速下降法

从下降的方向条件可知：$Jd=||J||cos\theta$,$\theta$表示方向和梯度方向的夹角，当$\theta =\pi$时：
$$d=\frac{-J^T}{||J||}$$
即梯度的负方向为最速下降方向，此时的缺点为最优值附件震荡，收敛慢。

b.牛顿法

在局部最优点$x^{\ast }$附近时，若$x+\Delta x$是最优解，则损失函数对$\Delta x$的导数等于0：
$$\frac{\partial }{\partial x}(F(x)+J\Delta x+\frac{1}{2}{\Delta }^{T}H\Delta x)=J^T+H\Delta x=0$$
可以得到 : $\Delta x=-H^{-1}{J}^T$，显然这种方法缺点非常明显，需要计算二阶导矩阵，计算比较复杂

c.高斯牛顿法

对残差函数$f(x)$一阶泰勒展开：
$$f(x+\Delta x)\approx \zeta (\Delta x)=f(x)+J\Delta x$$
需要注意的是这里的$J$代表的是残差函数$f(x)$的雅可比矩阵，我们带入损失函数有：
$$\begin{gathered} F(x+\Delta x)\approx L(\Delta x)=\frac{1}{2}\zeta (\Delta x{)}^T\zeta (\Delta x) \\ =F(x)+\Delta x^T{J}^{T}f+\frac{1}{2}\Delta x^T{J}^{T}J\Delta x \end{gathered}$$
令上述公式的一阶导为0，我们可以得到：
$$(J^{T}J)\Delta x_{gn}=-J^{T}f$$
常表述为：$H\Delta x_{gn}=b$

d.LM法

LM法是高斯牛顿法和最速下降法的一种结合：
$$(J^{T}J+uI)\Delta x_{lm}=-J^{T}fwithu\ge 0$$
相当于在求解过程中引入阻尼因子，其作用为：

• $u>0$保证$(J^{T}J+uI)$正定，迭代朝着下降的方向进行。
• $u$比较大时，$\Delta x_{lm}=-\frac{1}{u}{J}^{T}f=-\frac{1}{u}{F}^{\prime }(x{)}^T$,接近最速下降法。
• $u$比较小时，$\Delta x_{lm}\approx \Delta x_{gn}$,接近高斯牛顿法。