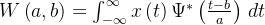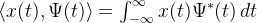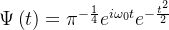一、小波计算公式
连续小波的计算公式:
其中,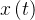
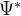
这个公式描述了如何将原始信号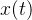

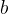
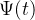
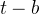
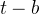
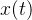
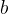
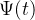
通过调整平移参数 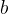
这种平移操作允许我们对信号的不同时间段进行分析,并在不同时间位置上捕获信号的局部特征。
总之,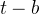
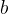
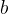
在小波分析中,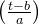
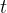

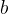
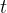
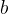

这种平移和尺度变换的操作使得小波函数能够适应不同尺度和时间位置上的信号特征。通过调整尺度参数 
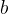
总之,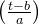
在小波分析中,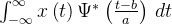
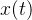
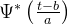
具体来说,这个内积运算可以被理解为信号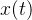
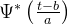
因此,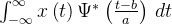
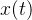
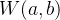

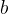
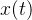
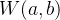
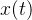

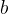
具体来说,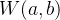

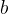
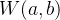
因此,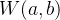

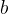
1. 内积的含义
在小波分析中,我们需要计算原始信号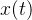
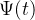
其中,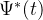
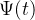
内积运算衡量了信号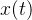
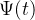
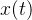
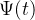
二、 Morlet小波函数的代入
现在,我们将Morlet小波函数代入到上述基本公式中,即将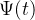
Morlet小波函数是小波分析中常用的一种小波函数,它的数学表达式如下:
其中:
- 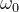
- 
- 
是一个常数,其数值为 ![\frac{1}{\sqrt[4]{\pi}}](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUNmcmFjJTdCMSU3RCU3QiU1Q3NxcnQlNUI0JTVEJTdCJTVDcGklN0QlN0Q%3D)
在小波分析中,归一化是非常重要的,因为它可以使得不同尺度下的小波函数具有相似的能量级,从而使得在不同尺度下进行比较和分析更为方便。
因此,
这个表达式可以看作是一个复指数函数与一个高斯函数的乘积。
复指数部分 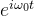
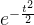
当我们考虑一个复指数函数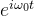
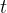
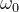
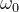
具体来说,复指数函数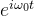
这个旋转的速度由频率参数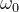
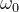
当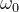
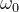
举个例子,假设
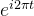
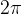
在时间轴上,这就对应着一个频率为

因此,复指数部分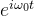
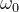
当我们说复指数函数
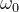
具体来说,当
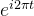
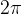
在小波分析中,复指数函数 


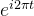

这是因为正弦波信号的周期是



因此,在时间轴上,复指数函数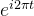
高斯函数部分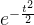
1. 高斯函数的形状:
高斯函数是一种钟形曲线,中心对称,其形状由 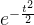
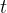

2.局部化作用:
在小波分析中,我们希望小波函数能够在时域上对信号进行局部分析,即只在某个时间段内对信号进行检测,而在其他时间段内不进行分析。高斯函数的局部化特性使得Morlet小波函数在时域上具有窄的主瓣和较宽的边瓣,使得在某个时间段内的信号贡献较大,而在其他时间段内的信号贡献较小,从而实现了对信号的局部化分析。
因此,高斯函数部分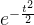
当将复指数函数部分
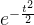
这个乘积可以写成
这样就得到了Morlet小波函数的实部部分。这个实部部分描述了信号在时域上的局部振荡特性,结合了正弦波的振荡和高斯窗口的局部化特性,用于在时域上对信号进行局部分析。
因此,高斯函数部分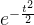
当将复指数函数部分
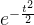
这个乘积可以写成
这样就得到了Morlet小波函数的实部部分。这个实部部分描述了信号在时域上的局部振荡特性,结合了正弦波的振荡和高斯窗口的局部化特性,用于在时域上对信号进行局部分析。
当将复指数函数部分
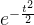
1. **复指数函数部分
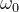
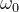

2. **高斯函数部分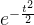

将这两部分相乘,得到的是Morlet小波函数的实部。这个实部函数描述了一个在时间轴上以给定频率 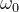
这个实部函数描述了一个振荡频率为 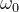
举个例子,当
这描述了一个频率为 1 Hz 的正弦波信号,并且在时间轴上以高斯窗口进行局部化。
在小波分析中,高斯窗口的宽度通常由尺度参数

我们知道,小波函数在时域和频域之间存在一种不确定性关系,即时域窄宽与频域窄宽之间存在权衡。具体来说,在频域上,小波函数的带宽(频率分辨率)与时域上窗口的宽度 
考虑到傅里叶变换对于高斯函数的性质,我们知道,高斯函数的傅里叶变换也是高斯函数。其带宽与时域高斯窗口的宽度
因此,当我们调整高斯窗口的宽度
具体来说:
- 当
- 当
因此,调整高斯窗口的宽度 
当我们将复指数函数 
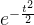
1. 频率调制:复指数函数
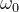

2.幅度调制:高斯函数 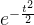
综合来说,乘积
Morlet小波函数在时域和频域上均具有良好的局部化特性,因此在时频分析中被广泛应用。它常用于处理周期性信号,如地震信号、心电图信号等。
对的,当我们在计算小波变换时,需要将Morlet小波函数代入到小波函数的复共轭中。Morlet小波函数的复共轭形式可以通过对其进行复共轭运算得到。让我们计算一下:
将Morlet小波函数
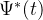
然后,我们将 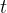

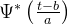

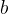
将这个复共轭形式代入到小波变换的积分公式中,我们就可以计算出小波变换系数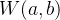
Morlet小波函数可以表示为:
在这个公式中,

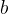
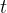
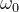
好的,让我们以一个具体的例子来说明。假设我们有一个信号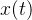

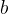
让我们选择 Morlet 小波函数作为我们的分析工具。假设我们使用的 Morlet 小波函数的频率参数 


现在,我们来计算 Morlet 小波函数在这些参数下的具体形式:
将参数代入:
这就是在尺度参数

现在,假设我们的信号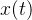

我们可以计算信号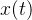
将信号和小波函数的具体形式代入:
通过计算这个积分,我们可以得到在尺度参数 


3.复共轭的引入:
我们知道,连续小波变换的公式中需要使用小波函数的复共轭。因此,我们需要求Morlet小波函数的复共轭,记为 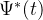
4.积分运算:
将原始信号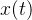
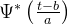

5. Morlet小波的连续小波变换公式:
将上述步骤的结果合并,我们得到了Morlet小波的连续小波变换公式:
这个公式描述了如何使用Morlet小波函数来对原始信号进行分析,从而得到连续尺度的小波变换系数
选择合适的小波函数是小波分析中的关键一步,它直接影响到小波变换的结果和分析效果。下面是一些选择合适小波函数的常见策略:
1. **理论选择**:根据所研究问题的特点和需求,选择与问题相关的小波函数。例如,Morlet小波适用于处理周期性信号,Daubechies小波适用于处理具有局部奇异性的信号等。
2. **频率特性**:选择小波函数时要考虑信号的频率特性。如果信号包含特定的频率成分,应选择能够捕获这些频率成分的小波函数。
3. **时域分辨率**:考虑小波函数在时域上的分辨率。某些小波函数具有较高的时域分辨率,可以捕获信号中的细微变化;而其他小波函数具有较低的时域分辨率,可以捕获信号中的整体结构。
4. **频域分辨率**:考虑小波函数在频域上的分辨率。某些小波函数具有较窄的频率范围,适用于分析局部频率特征;而其他小波函数具有较宽的频率范围,适用于分析整体频率分布。
5. **计算效率**:考虑小波函数的计算效率。有些小波函数具有简单的数学形式和快速的计算方法,适用于大规模数据分析和实时处理。
6. **交叉验证**:在实际应用中,可以尝试多种小波函数并进行交叉验证,选择最适合具体问题的小波函数。
综上所述,选择合适的小波函数需要综合考虑信号的特性、频率分布、时域分辨率、频域分辨率以及计算效率等因素,同时也可以通过理论分析和实验验证来确定最佳的选择。