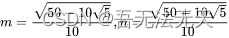系列文章目录

Unity 动态生成球体模型

前言

本篇主要讲解动态生成模型及球体模型创建思路

如何生成一个模型

在unity中生成一个模型至少需要两种数据，一是顶点位置，二是三角形连接顺序，一个模型是由若干个三角形组成，三角形连接顺序指的是模型中每个三角形的三个顶点所在的顶点数组的下标。需要将顶点位置存储在一个数组里，然后依据数组的下标，来确定顶点的连接顺序，例如生成一个三角形面的模型，需要3个顶点数据记为点a，点b，点c；它们在数组的下标分别为0，1，2；那么将a，b，c存储在一个数组里并且0，1，2在另一个数组里，最后顶点数据赋值给unity的Mesh类中的vertices变量三角形数据赋值给Mesh类中的triangles变量，即可得到一个三角形模型。0，1，2这些组成三角形的下标也不能随便进行组合，顺时针连接代表正面，逆时针代表反面，而一般情况下反面是不会被渲染的所以模型反面是看不到的。值得注意的是，是顺时针还是逆时针是由游戏中玩家的视角决定的，示例代码如下：

int[] triangles1 = { 0, 1, 2};//三角形连接顺序，这里是顺时针连接
Vector3[] vertices1 = new Vector3[3];//三角形顶点

//绘制一个顶部朝上的三角形
vertices1[0] = new Vector3(1, 0, 0);//左顶点
vertices1[1] = new Vector3(0, 1, 0);//上顶点
vertices1[2] = new Vector3(-1, 0, 0);//右顶点

Mesh mesh1 = new Mesh();//赋值给Mesh类
mesh1.vertices = vertices1;
mesh1.triangles = triangles1;


//创建另一个逆时针连接的三角形
int[] triangles2 = { 0, 1, 2 };//因为三角形是朝下的，所以0，1，2在这里是逆时针
Vector3[] vertices2 = new Vector3[3];

//绘制一个顶部朝下的三角形
vertices2[0] = new Vector3(1, 0, 0);//左顶点
vertices2[1] = new Vector3(0, -1, 0);//下顶点
vertices2[2] = new Vector3(-1, 0, 0);//右顶点

Mesh mesh2 = new Mesh();
mesh2.vertices = vertices2;
mesh2.triangles = triangles2;

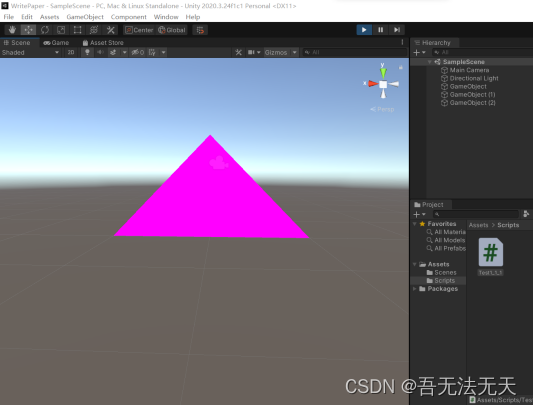
效果如下：

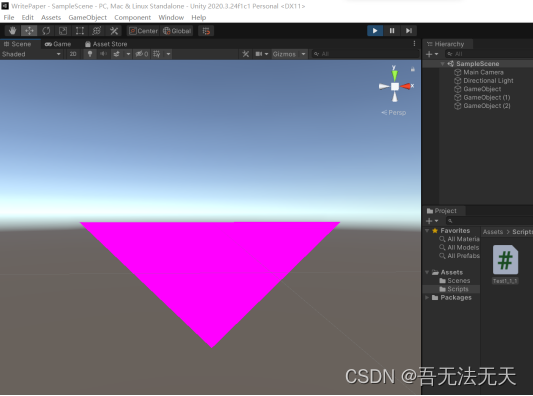
可以看到，只有顶点朝上的三角形渲染了出来，顶点朝下的三角形并没有被渲染，因为没有提供材质，所以它是紫色的，表示材质错误，这个我们先不用管。当转过反面时，即可看到顶点向下的三角形被渲染了出来，向上的消失（注意看右上角x轴的方向）：

球体模型的创建方法

解决了模型生成问题，接下来要解决的是，如何生成一个球体模型。游戏中的模型是由一个一个的三角形面所构成，要构成一个球体模型，我们需要很多的三角形面去组合得到一个近似球体的模型，并不能得到一个完美的球体，不过主要三角形面足够多，那单凭肉眼也很难区分与完美球体的区别。
在我查阅的资料中，有的是使用一个正方体对正方体的各个面进行细分，比如一个面细分成为若干个面最后乘上半径，即可得到一个球体模型，类似于把一个正方体的箱子把它撑起来变得圆圆地，但这样会产生一个问题，那就是越靠近正方体的角，三角面会越小，顶点越密集。原因是一个正方体膨胀起来，它的边中间部分会被拉长得最厉害，而越靠近顶点被拉长得越小，就导致了远离顶点位置的三角形面被放大更多，靠近顶点位置的放大更少，所以靠近正方体顶点位置的顶点越密集，这时候需要一些算法去进行优化。
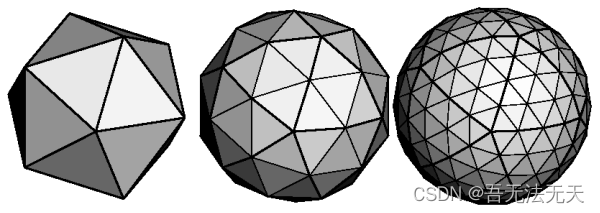
我的方法是细分正二十面体，这样就可以避免以上问题，并且在实践中效果也不错。正二十面体的每个面是三角形，细分这些三角形，最后乘上一个半径，即可得到一个近似球体，如下图所示：

计算正二十面体

正二十面体顶点

正二十面体由12个面，12个顶点构成，如果是以（0，0，0）为中心点，外界球半径为1，那么它的各个顶点的坐标为{(±m,0,±n), (0,±n,±m), (±n,±m,0)}，其中
（图片有水印看不清可以看这里）。

三角形连接顺序

顶点的位置的计算搞定了，接下来要考虑如何摆放和连接这些点使它们跟构成正二十面体上的三角面。
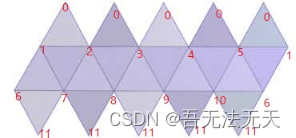
首先看一下正二十面体的展开图：

我们先不考虑顶点在数组存放的位置问题，先给展开图的每个顶点赋予一个标号，0~11分别对应了正二十面体的12个顶点。通过展开图，我们发现：顶部顶点标号都是0，底部的都是11，第二列和第三列的标号前5项差值为1的等差数列，但最后一项与第一项一样。通过这些信息，我们可以用一个5次的循环将它们进行顺时针连接，每一次循环可以连接4个三角形：

int[] triangles = new int[12 * 5];

int index = 0;
for (int i = 0; i < 5; i++)
{
	triangles[index++] = 0;
	triangles[index++] = i + 1;
	triangles[index++] = (i == 4 ? 1 : i + 2);

	triangles[index++] = i + 1;
	triangles[index++] = i + 6;
	triangles[index++] = (i == 4 ? 1 : i + 2);

	triangles[index++] = i + 1;
	triangles[index++] = (i == 0 ? 10 : i + 5);
	triangles[index++] = i + 6;

	triangles[index++] = (i == 0 ? 10 : i + 5);
	triangles[index++] = 11;
	triangles[index++] = i + 6;
}

最后，我们再把这些展开图的标号映射到正二十面体上对应的数组位置：

展开图的标号就映射成了每个顶点在数组中对应的位置，这样模型必须的两个数据：顶点数组和三角形连接顺序就有了，就可以生成一个正二十面体的模型，为了方便观察，这里赋予了一个临时的材质，并且显示出模型的线框。

至于细分三角形的实现，需要在之后的文章中，结合动态LOD技术进行实现。