关于对N皇后问题和回溯法的理解 个人非常推荐下面这个视频:算法与数据结构,回溯法求解八皇后,最经典的递归问题_哔哩哔哩_bilibili八皇后问题是计算机科学中最为经典的问题之一,该问题由国际西洋棋棋手马克斯·贝瑟尔于1848年提出。八皇后问题,即在8×8的国际象棋盘上摆放八个皇后,使其不能互相攻击,任意两个皇后都不能处于同一行、同一列或同一斜线上,求出一共有多少种摆放方式,每种摆放方式的具体摆法。
视频中的代码使用C++写的,个人接触嵌入式较多所以比较习惯用C
C语言代码如下:
/* N皇后问题 */
#include <stdio.h>
#include <stdlib.h>
#define N 100 //宏定义最大的N
int attack[N][N];
char queen[N][N];
int cnt;
void init(int n);//初始化attack和queen数组
void print(int n);//打印符合要求的摆法
void print_ack(int n);//测试update_ack函数编写是否正确
void copy(int object[N][N],int target[N][N],int n);//将对象数组保存给目标数组
void update_ack(int x,int y,int n);//摆放queen后更新attack数组,将进queen攻路线上的值标为1
void backtrack(int row,int n);//回溯法 递归调用
int main(int argc, char const *argv[])
{
int n;
puts("Please input the N of queen:");
scanf("%d",&n);//计算nXn的皇后问题
init(n);//初始化attack和queen数组
backtrack(0,n);//从第0行开始摆放queen
printf("The number of required placement method =%d\n",cnt);
system("pause");
return 0;
}
void backtrack(int row,int n)
{
if(row==n)//递归执行到摆放完所有行的结束条件
{
cnt++;
print(n);
return ;
}
int col;
for(col=0;col<n;col++)
{
if(attack[row][col]==0)//判断该位置是能够放置queen
{
int tem[N][N];//保存当前的attack数组内容,便于回溯
copy(attack,tem,n);//遍历交换
queen[row][col]='Q';//该位置放置queen
update_ack(row,col,n);//放置完后将棋盘上queen的进攻路线全部标为1
backtrack(row+1,n);//行数+1,递归回到函数头部重复判断
//递归结束才会执行下面的语句
copy(tem,attack,n);//将之前保存的temp返还给attack
queen[row][col]='.';//将标记的Q改回.
}
}
}
void init(int n)//初始化attack和queen数组
{
int i,j;
for(i=0;i<n;i++)//对二维数组遍历
for(j=0;j<n;j++)
{
attack[i][j]=0;
queen[i][j]='.';
}
}
void print(int n)//打印符合要求的摆法
{
int i,j;
printf("cnt=%d\n",cnt);
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
{
printf("%c\t",queen[i][j]);
}
printf("\n");
}
printf("\n");
}
void print_ack(int n)//测试update_ack函数编写是否正确
{
int i,j;
for(i=0;i<n;i++)//对二维数组遍历
{
for(j=0;j<n;j++)
{
printf("%d\t",attack[i][j]);
}
printf("\n");//每打印出n个换行
}
}
void copy(int object[N][N],int target[N][N],int n)//将对象数组保存给目标数组
{
int i,j;
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
{
target[i][j]=object[i][j];
}
}
/* for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
{
printf("%d\t",tem[i][j]);
}
printf("\n");
} */
}
void update_ack(int x,int y,int n)
{
int i,j,nx,ny;
int dx[8]={-1,0,1,-1, 1,-1,0,1};//dx,dy的八对数 分别对应
int dy[8]={-1,-1,-1,0, 0, 1, 1,1 };//左上,上,右上,左,右,左下,下,右下,八个方向
attack[x][y]=1;
for(i=1;i<n;i++)
{
for(j=0;j<8;j++)
{
nx=x+i*dx[j];
ny=y+i*dy[j];
if(nx>=0 && nx<n && ny>=0 && ny<n )//nx,ny判断是否在棋盘内,满足才将对应的位标记
{
attack[nx][ny]=1;
}
}
}
// print_ack(n);测试代码
}(N可以随意取,大于100的话需要修改宏定义 #define N 100 )
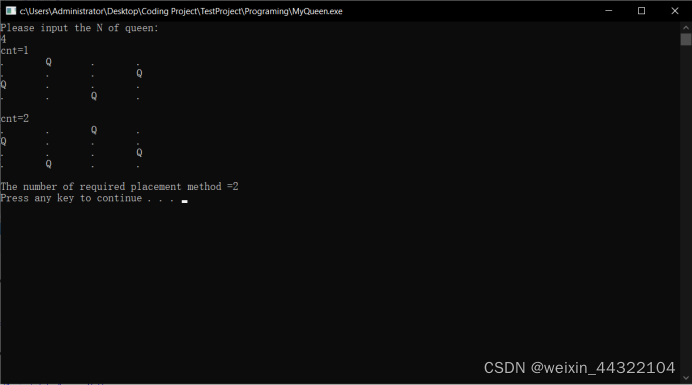
代码运行结果:
如果这篇Blog有帮到你,请点个赞再走,Respect 所有帮到过我的博客作者!