搜索树
完整可编译运行代码见:Github::Data-Structures-Algorithms-and-Applications/_33Search tree
概述
二叉搜索树的性能:查找、插入或者删除操作所需要的平均时间为 Θ \Theta Θ(logn),而最坏情况下的时间为 Θ \Theta Θ(n)(当二叉搜索树的高度为n时具有最坏时间复杂度);元素按升序输出时所需时间为 Θ \Theta Θ(n)。
散列表与二叉搜索树:散列的查找、插入或者删除操作最坏时间复杂度为 Θ \Theta Θ(n),但是散列表在最好的情况下具有超级性能 Θ \Theta Θ(1)。
寻找最接近关键字的问题:二叉搜索树时间复杂度 Θ \Theta Θ(n)。散列表的时间复杂度为 Θ \Theta Θ(n+D),其中D是散列表除数。跳表的时间复杂度为 Θ \Theta Θ(logn)。
定义
二叉搜索树
散列表的缺陷
使用散列表存储字典,字典操作操作(查找、插人和删除)所需要的平均时间为 Θ ( 1 ) \Theta (1) Θ(1)。而这些操作在最坏情况下的时间与字典的元素个数n呈线性关系。如果给dictionary 增加以下操作,那么散列不再具有较好的平均性能:
1)按关键字的升序输出字典元素。
-
散列表:需要从表中收集数据,排序,然后输出。如果使用除数为D的链表,那么能用O(D+n)时间收集元素,用O(nlogn)时间排序,用O(n)时间输出,因此总时间为O(D+nlogn)。
-
平衡二叉树:能在 Θ ( n ) \Theta (n) Θ(n)时间内完成。
2)按升序找到第k个元素。
-
散列表:能在O(D+n)时间内完成。
-
索引平衡搜索树:能在O(logn)时间内完成。
3)删除第k个元素。
-
散列表:能在O(D+n)时间内完成。
-
索引平衡搜索树:能在O(logn)时间内完成。
定义
**定义14-1二叉搜索树(binary search tree)**是一棵二叉树,可能为空;一棵非空的二叉搜索树满足以下特征:
-
1)每个元素有一个关键字,并且任意两个元素的关键字都不同;因此,所有的关键字都是唯一的。
-
2)在根节点的左子树中,元素的关键字(如果有的话)都小于根节点的关键字。
-
3)在根节点的右子树中,元素的关键字(如果有的话)都大于根节点的关键字。
-
4)根节点的左、右子树也都是二叉搜索树。
有重复值的二叉搜索树:
-
1)每个元素有一个关键字,元素的关键字可以不唯一。
-
2)在根节点的左子树中,元素的关键字(如果有的话)都小于等于根节点的关键字。
-
3)在根节点的右子树中,元素的关键字(如果有的话)都大于等于根节点的关键字。
-
4)根节点的左、右子树也都是有重复值的二叉搜索树。
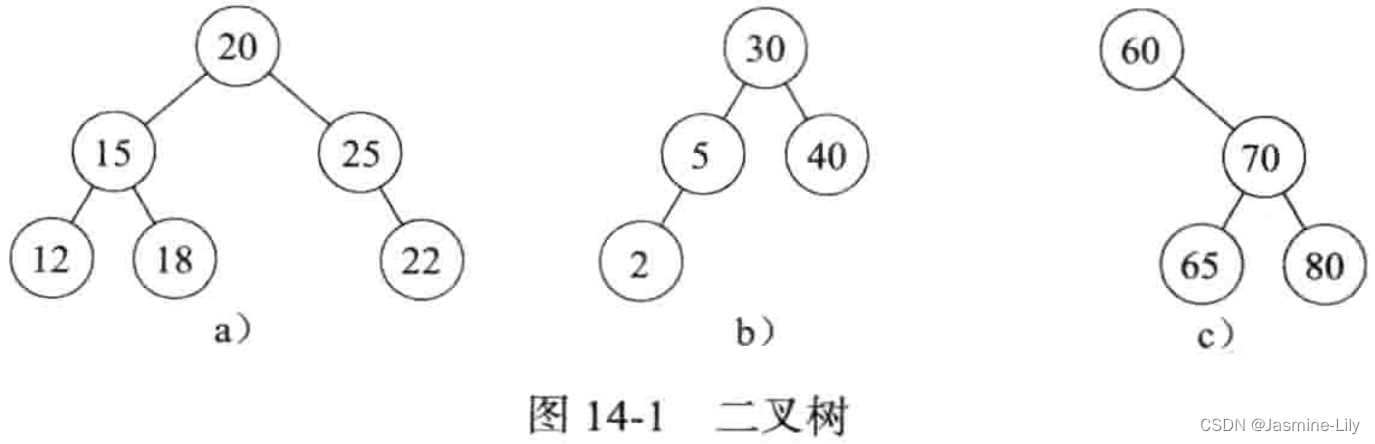
如图14-1 a)不是二叉搜索树,因为根节点的右子树不是二叉搜索树。图14-1b) c)是二叉搜索树。
索引二叉搜索树
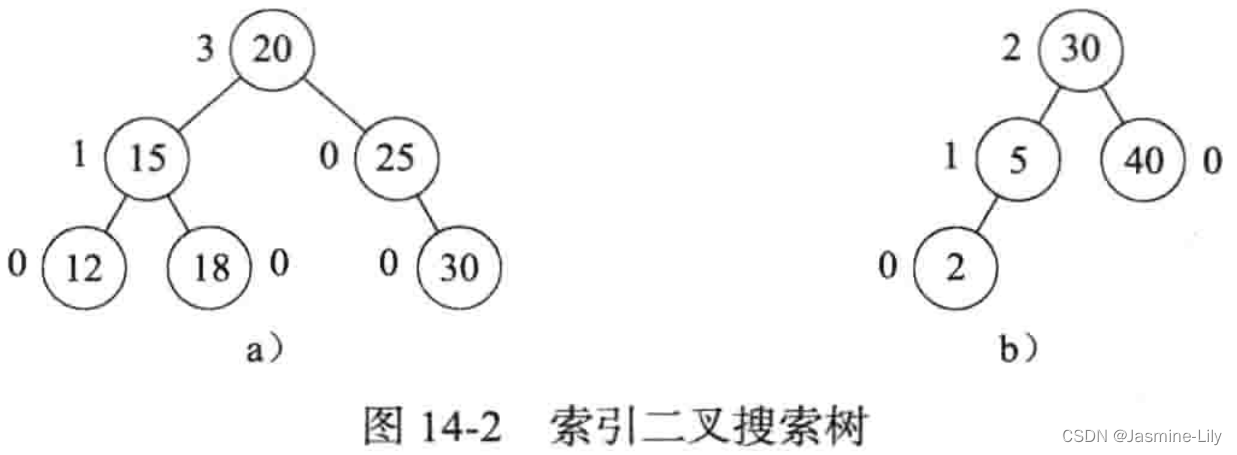
索引二叉搜索树(indexed binary search tree)源于普通二叉搜索树,只是在每个节点中添加一个leftSize域。这个域的值是该节点左子树的元素个数。图14-2是两棵索引二叉搜索树。节点内的数字是元素的关键字,节点外的数字是leftSize的值。注意,leftSize同时给出了一个元素的索引(该元素的左子树的元素排在该元素之前)(只在最左边的这一条路径有效,所有的右子树都不满足这个规则)。例如,在图14-2a的根为20的子树中,元素按顺序分别为12,15,18,20,25和30。依照线性表的形式 ( e 0 , e 1 , . . . , e 4 ) (e_0,e_1,...,e_4) (e0,e1,...,e4),根的索引是3,它等于根元素的leftSize域的值。
抽象数据类型
二叉搜索树的抽象数据类型
索引二叉搜索树的抽象数据类型
二叉搜索树的操作和实现
搜索
假设要查找关键字为theKey的元素。先从根开始查找。如果根为空,那么搜索树不包含任何元素,即查找失败。如果不空,则将 theKey与根的关键字相比较。如果 theKey小,那么就不必在右子树中查找,只要查找左子树。如果theKey大,则正好相反,只需查找右子树。如果 theKey等于根的关键字,则查找成功。时间复杂度为O(logn)。
插入
假设要在二叉搜索树中插人一个新元素thePair,首先要通过查找来确定,在树中是否存在某个元素,其关键字与thePair.first 相同。如果搜索成功,那么就用 thePair.second 替代该元素的值。如果搜索不成功,那么就将新元素作为搜索中断节点的孩子插入二叉搜索树。在搜索中能找到键值与thePair.first相近的节点pp,当thePair.second < pp.second时,将thePair作为pp的左孩子;反之,将thePair作为pp的右孩子。在插入元素后,treeSize++。
删除
三种情况:
1)p是树叶;
要删除的节点是叶节点。存储叶节点到temp,将叶节点的父节点的左孩子置为nullptr,释放叶节点temp空间。若是根节点,直接释放根节点空间,令根为 nullptr。
2)p只有一棵非空子树;
要删除的节点p只有一棵子树。如果p没有父节点(即p是根节点),则p的唯一子树的根节点成为新的搜索树的根节点。如果p有父节点pp,则修改pp的指针域,使得它指向p的唯一孩子,然后释放节点p。
3)p有两棵非空子树。
先将该节点的元素替换为它的左子树的最大元素或右子树的最小元素,然后把替换元素的节点删除。本文使用左子树的最大元素替换。
要在一个节点的左子树中查找关键字最大的元素,先移动到左子树的根,然后沿着右孩子指针移动,直到右孩子指针为nullptr的节点为止。类似地,要在一个节点的右子树中查找关键字最小的元素,先移动到右子树的根,然后沿着左孩子指针移动,直到左孩子指针为nullptr的节点为止。
代码
/*
Project name : _33Search_tree
Last modified Date: 2023年12月21日11点13分
Last Version: V1.0
Descriptions: 二叉搜索树——模板类实现
*/
#ifndef _33SEARCH_TREE_BINARYSEARCHTREE_H
#define _33SEARCH_TREE_BINARYSEARCHTREE_H
#include "bsTree.h"
#include "binaryTreeNode.h"
using namespace std;
void binarySearchTreeTest();
template<class K, class E>
class binarySearchTree : public bsTree<K,E>
{
public:
binarySearchTree(){
root = nullptr;
treeSize = 0;
}
// 字典相关的方法
bool empty() const {return treeSize == 0;}
int size() const {return treeSize;}
pair<K, E>* find(const K theKey) const;
void insert(const pair<K, E> thePair);
void erase(const K theKey);
/*中序遍历二叉树,使用函数指针的目的是是的本函数可以实现多种目的*/
void inOrder(void(*theVisit)(binaryTreeNode<pair<K, E>>*))
{
visit = theVisit;
/*是因为递归,所以才要这样的*/
inOrder(root);/*这里调用的是静态成员函数inOrder()*/
}
/*中序遍历---输出endl*/
void inOrderOutput() { inOrder(output); cout << endl; }
// additional method of bsTree
void ascend() {inOrderOutput();}
private:
binaryTreeNode<pair<K, E>>* root;//指向根的指针
int treeSize;//树的结点个数
static void (*visit)(binaryTreeNode<pair<K, E>>*);//是一个函数指针,返回值为void 函数参数为binaryTreeNode<pair<K, E>>*
static void output(binaryTreeNode<pair<K, E>>* t) { cout << t->element << " "; }
static void inOrder(binaryTreeNode<pair<K, E>>* t);
};
/*私有静态成员初始化*/
/*这里是静态函数指针成员的初始化,不初始化会引发LINK错误*/
template<class K, class E>
void (*binarySearchTree<K,E>::visit)(binaryTreeNode<pair<K, E>>*) = 0; // visit function
/*中序遍历 递归*/
template<class K, class E>
void binarySearchTree<K,E>::inOrder(binaryTreeNode<pair<K, E>>* t)
{
if (t != nullptr)
{
inOrder(t->leftChild);/*中序遍历左子树*/
visit(t);/*访问树根*/
inOrder(t->rightChild);/*中序遍历右子树*/
}
}
/* 查找元素
* 输入:theKey表示需要查找元素的键值
* 输出:键值为theKey的节点的pair地址
* 时间复杂度:O(logn),n表示节点个数
*/
template<class K, class E>
pair<K, E>* binarySearchTree<K,E>::find(K theKey) const
{
// 返回值是匹配数对的指针
// 如果没有匹配的数对,返回值为nullptr
// p从根节点开始搜索,寻找关键字等于theKey的一个元素
binaryTreeNode<pair<K, E> > *p = root;
while (p != nullptr)
// 检查元素 p->element
if (theKey < p->element.first)
p = p->leftChild;
else
if (theKey > p->element.first)
p = p->rightChild;
else // 找到匹配的元素
return &p->element;
// 没找到匹配的元素
return nullptr;
}
/*
* 插入元素
* 输入:const pair<K, E> thePair表示需要插入的键值对
* 输出:void
* 时间复杂度:O(logn),表示节点个数
*/
template<class K, class E>
void binarySearchTree<K,E>::insert(const pair<K, E> thePair)
{
// 插入thePair. 如果该键值存在则覆盖元素
// 寻找插入位置
binaryTreeNode<pair<K, E> > *p = root,
*pp = nullptr;
while (p != nullptr)
{// 检查元素 p->element
pp = p;
// 如果当前键值小于p的键值,则移到p的左孩子
if (thePair.first < p->element.first)
p = p->leftChild;
else// 如果当前键值大于p的键值,则移到p的右孩子
if (thePair.first > p->element.first)
p = p->rightChild;
else
{// 如果键值相等,覆盖旧的值
p->element.second = thePair.second;
return;
}
}
// 为thePair建立一个节点,然后与pp链接,此时pp是叶子节点
auto *newNode = new binaryTreeNode<pair<K, E> > (thePair);
if (root != nullptr) // 树非空
// 如果thePair的键值小于pp的键值,则将thePair作为pp的左孩子,反之将其作为右孩子
if (thePair.first < pp->element.first)
pp->leftChild = newNode;
else
pp->rightChild = newNode;
else// 树空
root = newNode; // 直接将thePair节点作为根节点
treeSize++;
}
/*
* 删除元素
* 输入:const K theKey表示需要删除元素的键值
* 输出:void
* 时间复杂度:O(logn),n表示节点个数
*/
template<class K, class E>
void binarySearchTree<K,E>::erase(const K theKey)
{
// 删除关键字等于theKey的数对
// 查找关键字为theKey的节点
binaryTreeNode<pair<K, E> > *p = root,
*pp = nullptr;
while (p != nullptr && p->element.first != theKey)
{
pp = p;
if (theKey < p->element.first)
p = p->leftChild;
else
p = p->rightChild;
}
if (p == nullptr)
return; // 不存在与关键字theKey匹配的数对
// 重新组织树结构
// 当p有两个孩子时的处理
if (p->leftChild != nullptr && p->rightChild != nullptr)
{
// 两个孩子
// 在P的左子树中寻找最大元素
binaryTreeNode<pair<K, E> > *s = p->leftChild,
*ps = p; // s的父节点
while (s->rightChild != nullptr)
{// 移动到更大的pair
ps = s;
s = s->rightChild;// 右孩子比较大
}
// 将最大元素s移到p
// p->element = s->element 的键值是 const
// 当最大值就是p的左孩子时,new的元素不能直接指向p的左孩子,而要指向p的左孩子的左孩子(此时p的左孩子没有右孩子),因为到时候s会被delete掉,这个问题在后面的p至多有一个孩子那里解决的
binaryTreeNode<pair<K, E> >* q = nullptr;
q = new binaryTreeNode<pair<K, E> >(s->element, p->leftChild, p->rightChild);
// pp是p的父节点
// 如果p没有父节点
if (pp == nullptr)
root = q;
else if (p == pp->leftChild)// 如果p是pp的左孩子
pp->leftChild = q;
else// 如果p是pp的右孩子
pp->rightChild = q;
// 如果s的父节点就是p,说明p节点的左子树只有左子树没有右子树
// 那么删除p后pp就是其父节点
if (ps == p) pp = q;
else pp = ps;// 反之ps是其父节点
delete p;
p = s;
}
// p至多只有一个孩子
// 把孩子的指针存放到c
binaryTreeNode<pair<K, E> > *c;
if (p->leftChild != nullptr)
c = p->leftChild;
else
c = p->rightChild;
// 删除p
if (p == root)
root = c;
else
{// p是pp的左孩子还是右孩子
if (p == pp->leftChild)
pp->leftChild = c;
else pp->rightChild = c;
}
treeSize--;
delete p;
}
// overload << for pair
template <class K, class E>
ostream& operator<<(ostream& out, const pair<K, E>& x)
{out << x.first << ' ' << x.second; return out;}
#endif //_33SEARCH_TREE_BINARYSEARCHTREE_H
有重复值的二叉搜索树的操作与实现
和二叉搜索树的实现几乎一致。只需要更改在插入元素时,更改代码:
// 如果当前键值小于p的键值,则移到p的左孩子
if (thePair.first < p->element.first)
p = p->leftChild;
else// 如果当前键值大于p的键值,则移到p的右孩子
if (thePair.first > p->element.first)
p = p->rightChild;
else
{// 如果键值相等,覆盖旧的值
p->element.second = thePair.second;
return;
}
为:
// 如果当前键值小于等于p的键值,则移到p的左孩子
if (thePair.first <= p->element.first)
p = p->leftChild;
else// 如果当前键值大于p的键值,则移到p的右孩子
p = p->rightChild;
索引二叉搜索树的操作与实现
搜索
键值搜索
根据键值的搜索与二叉搜索树的一致。
索引搜索
从根节点cur开始搜索,当cur节点的索引大于index时,cur移动到其左孩子;当cur节点的索引小于index时,修改index为index-(cur->leftSize + 1),cur移动到其右孩子;直到cur->leftSize = cur或者cur为空,结束循环。
结束循环后,当cur为空,说明没有找到索引为index的节点,返回nullptr;当cur不为空,则返回cur->element的地址。
插入
插入元素的流程与二叉搜索树的流程差不多,但是需要更新索引的值。当插入元素的键值在原树中存在时,也就是插入元素只需要更新元素时,不需要更新索引的值;反之,需要更新索引的值。
更新索引:从根节点开始搜索,当当前节点的键值大于插入元素的键值时,需要将当前节点的父亲节点的leftSize++,并将当前节点移动到当前节点的左孩子;当当前节点的键值小于等于插入元素的键值时,需要将当前节点移动到当前节点的右孩子;每更新一次当前节点,就需要更新记录其父节点的变量。
删除
删除元素的流程与二叉搜索树的流程差不多,但是需要更新索引的值。当p是root节点时,不需要更新索引,其他时候需要更新索引,因此下面的步骤只考虑p不是root节点的情况。
更新索引的值分为两步,当找到需要删除的节点时,需要寻找大于p的键值的最小键值节点并记录其键值为bigger。如果p是其父亲的左孩子,当p的右孩子为空时,bigger为其父亲节点的键值;当p的右孩子不为空时,bigger为其右孩子的键值。如果p是其父亲节点的右孩子时,如果p的右孩子不为空,则bigger是p的右孩子的键值;如果p的右孩子为空,则记录bigger为p的键值,此处是特殊情况,目的是不更新p的右孩子的索引。
在删除节点完成之后,需要根据bigger的值更新索引。从根节点开始搜索,当bigger小于当前节点的键值时,将当前节点的父亲节点的leftSize–,并将当前节点移动到当前节点的左孩子;当bigger大于当前节点的键值时,将当前节点移动到当前节点的右孩子;当bigger等于当前节点的键值时,终止循环,此处的目的是不更新所删除节点的右孩子的索引。
代码
/*
Project name : _33Search_tree
Last modified Date: 2023年12月21日11点13分
Last Version: V1.0
Descriptions: 二叉搜索树——索引二叉树的模板类
*/
#ifndef _33SEARCH_TREE_INDEXEDBINARYSEARCHTREE_H
#define _33SEARCH_TREE_INDEXEDBINARYSEARCHTREE_H
#include "indexedBSTree.h"
#include "indexedBinarySearchTreeNode.h"
using namespace std;
void indexedBinarySearchTreeTest();
template<class K, class E>
class indexedBinarySearchTree : public indexedBSTree<K, E> {
public:
indexedBinarySearchTree() {
root = nullptr;
treeSize = 0;
}
// 字典相关的方法
[[nodiscard]] bool empty() const { return treeSize == 0; }
[[nodiscard]] int size() const { return treeSize; }
pair<K, E> *find(const K theKey) const;
// index从0开始
[[nodiscard]] pair<K, E>* get(int index) const;
void insert(const pair<K, E> thePair);
void erase(const K theKey);
/*中序遍历二叉树,使用函数指针的目的是是的本函数可以实现多种目的*/
void inOrder(void(*theVisit)(indexedBinarySearchTreeNode<pair<K, E>> *)) {
visit = theVisit;
/*是因为递归,所以才要这样的*/
inOrder(root);/*这里调用的是静态成员函数inOrder()*/
}
/*中序遍历---输出endl*/
void inOrderOutput() {
inOrder(output);
cout << endl;
}
/*前序遍历二叉树,使用函数指针的目的是是的本函数可以实现多种目的*/
void preOrder(void(*theVisit)(indexedBinarySearchTreeNode<pair<K, E>> *))
{
visit = theVisit;
/*是因为递归,所以才要这样的*/
preOrder(root);/*这里调用的是成员函数,preOrder()*/
}
/*前序遍历---输出endl*/
void preOrderOutput() { preOrder(output); cout << endl; }
// additional method of bsTree
void ascend() { inOrderOutput(); }
private:
indexedBinarySearchTreeNode<pair<K, E>> *root;//指向根的指针
int treeSize;//树的结点个数
static void (*visit)(indexedBinarySearchTreeNode<pair<K, E>> *);//是一个函数指针,返回值为void 函数参数为indexedBinarySearchTreeNode<pair<K, E>>
static void output(indexedBinarySearchTreeNode<pair<K, E>> *t) { cout << *t << " "; }
static void inOrder(indexedBinarySearchTreeNode<pair<K, E>> *t);
static void preOrder(indexedBinarySearchTreeNode<pair<K, E>> *t);
};
/*私有静态成员初始化*/
/*这里是静态函数指针成员的初始化,不初始化会引发LINK错误*/
template<class K, class E>
void
(*indexedBinarySearchTree<K, E>::visit)(indexedBinarySearchTreeNode<pair<K, E>> *) = 0; // visit function
/*中序遍历 递归*/
template<class K, class E>
void indexedBinarySearchTree<K, E>::inOrder(indexedBinarySearchTreeNode<pair<K, E>> *t) {
if (t != nullptr) {
inOrder(t->leftChild);/*中序遍历左子树*/
visit(t);/*访问树根*/
inOrder(t->rightChild);/*中序遍历右子树*/
}
}
/*二叉树的普通成员函数*/
/*前序遍历 递归*/
template<class K, class E>
void indexedBinarySearchTree<K, E>::preOrder(indexedBinarySearchTreeNode<pair<K, E>> *t)
{
if (t != nullptr)
{
visit(t);/*访问树根*/
preOrder(t->leftChild);/*前序遍历左子树*/
preOrder(t->rightChild);/*前序遍历右子树*/
}
}
/* 根据键值查找元素
* 输入:theKey表示需要查找元素的键值
* 输出:键值为theKey的节点的pair地址
* 时间复杂度:O(logn),n表示节点个数
*/
template<class K, class E>
pair<K, E> *indexedBinarySearchTree<K, E>::find(K theKey) const {
// 返回值是匹配数对的指针
// 如果没有匹配的数对,返回值为nullptr
// p从根节点开始搜索,寻找关键字等于theKey的一个元素
indexedBinarySearchTreeNode<pair<K, E> > *p = root;
while (p != nullptr)
// 检查元素 p->element
if (theKey < p->element.first)
p = p->leftChild;
else if (theKey > p->element.first)
p = p->rightChild;
else // 找到匹配的元素
return &p->element;
// 没找到匹配的元素
return nullptr;
}
/*
* 根据索引查找元素
* 输入:int index表示查找节点的索引
* 输出:索引为index的节点的pair地址
*/
template<class K, class E>
pair<K, E>* indexedBinarySearchTree<K, E>::get(int index) const {
indexedBinarySearchTreeNode<pair<K, E> >* cur = root;
while(cur != nullptr && cur->leftSize != index){
// 当前节点的索引大于index,移动到左孩子
if(cur->leftSize > index)
cur = cur->leftChild;
else{// 当前节点的索引小于index,移动到右孩子
index = index - (cur->leftSize + 1);
cur = cur->rightChild;
}
}
if(cur == nullptr)
return nullptr;
else
return &(cur->element);
}
/*
* 插入元素
* 输入:const pair<K, E> thePair表示需要插入的键值对
* 输出:void
* 时间复杂度:O(logn),表示节点个数
*/
template<class K, class E>
void indexedBinarySearchTree<K, E>::insert(const pair<K, E> thePair) {
// 插入thePair. 如果该键值存在则覆盖元素
// 寻找插入位置
indexedBinarySearchTreeNode<pair<K, E> > *p = root,
*pp = nullptr;
while (p != nullptr) {// 检查元素 p->element
pp = p;
// 如果当前键值小于p的键值,则移到p的左孩子
if (thePair.first < p->element.first)
p = p->leftChild;
else// 如果当前键值大于p的键值,则移到p的右孩子
if (thePair.first > p->element.first)
p = p->rightChild;
else {// 如果键值相等,覆盖旧的值
p->element.second = thePair.second;
return;
}
}
// 为thePair建立一个节点,然后与pp链接,此时pp是叶子节点
auto *newNode = new indexedBinarySearchTreeNode<pair<K, E> >(thePair);
if (root != nullptr) // 树非空
// 如果thePair的键值小于pp的键值,则将thePair作为pp的左孩子,反之将其作为右孩子
if (thePair.first < pp->element.first) {
pp->leftChild = newNode;// pp的左孩子指向插入的元素,因此pp的索引要更改为1
} else
pp->rightChild = newNode;
else// 树空
root = newNode; // 直接将thePair节点作为根节点
treeSize++;
// 修改索引的值,此时刚加入的元素的leftSize需要调整
p = root;
while (p != nullptr) {// 检查元素 p->element
pp = p;
// 如果当前键值小于p的键值,则移到p的左孩子
if (thePair.first < p->element.first){
pp->leftSize++;
p = p->leftChild;
}
else // 如果当前键值小于等于p的键值,则移到p的右孩子
p = p->rightChild;
}
}
/*
* 删除元素
* 输入:const K theKey表示需要删除元素的键值
* 输出:void
* 时间复杂度:O(logn),n表示节点个数
*/
template<class K, class E>
void indexedBinarySearchTree<K, E>::erase(const K theKey) {
// 删除关键字等于theKey的数对
// 查找关键字为theKey的节点
indexedBinarySearchTreeNode<pair<K, E> > *p = root,
*pp = nullptr;
bool flag = false; // 用来记录是否需要重新组织索引
while (p != nullptr && p->element.first != theKey) {
pp = p;
if (theKey < p->element.first)
p = p->leftChild;
else
p = p->rightChild;
}
if (p == nullptr)
return; // 不存在与关键字theKey匹配的数对
// 如果删除节点就是根节点,则其他节点的索引无需改变
if(p != root)
flag = true;
// bigger存储比p大的最小的键值,后面用于删除元素后索引的更新
K bigger = p->element.first;
if(pp != nullptr){
if(p == pp->leftChild){
if(p->rightChild == nullptr)
bigger = pp->element.first;
else
bigger = p->rightChild->element.first;
}
else if(p->rightChild != nullptr)
bigger = p->rightChild->element.first;
else
bigger = p->element.first;// 此时记录为p的键值的目的是不更新p的右孩子的索引
}
cout << "bigger = " << bigger << endl;
// 重新组织树结构
// 当p有两个孩子时的处理
if (p->leftChild != nullptr && p->rightChild != nullptr) {
// 两个孩子
// 在P的左子树中寻找最大元素
indexedBinarySearchTreeNode<pair<K, E> > *s = p->leftChild,
*ps = p; // s的父节点
while (s->rightChild != nullptr) {// 移动到更大的pair
ps = s;
s = s->rightChild;// 右孩子比较大
}
// 将最大元素s移到p
// p->element = s->element 的键值是 const
// 当最大值就是p的左孩子时,new的元素不能直接指向p的左孩子,而要指向p的左孩子的左孩子(此时p的左孩子没有右孩子),因为到时候s会被delete掉,这个问题在后面的p至多有一个孩子那里解决的
indexedBinarySearchTreeNode<pair<K, E> > *q = nullptr;
q = new indexedBinarySearchTreeNode<pair<K, E> >(s->element, s->leftSize, p->leftChild, p->rightChild);
// pp是p的父节点
// 如果p没有父节点
if (pp == nullptr)
root = q;
else if (p == pp->leftChild)// 如果p是pp的左孩子
pp->leftChild = q;
else// 如果p是pp的右孩子
pp->rightChild = q;
// 如果s的父节点就是p,说明p节点的左子树只有左子树没有右子树
// 那么删除p后pp就是其父节点
if (ps == p) pp = q;
else pp = ps;// 反之ps是其父节点
delete p;
p = s;
}
// p至多只有一个孩子
// 把孩子的指针存放到c
indexedBinarySearchTreeNode<pair<K, E> > *c;
if (p->leftChild != nullptr)
c = p->leftChild;
else
c = p->rightChild;
// 删除p
if (p == root)
root = c;
else {// p是pp的左孩子还是右孩子
if (p == pp->leftChild)
pp->leftChild = c;
else pp->rightChild = c;
}
treeSize--;
delete p;
// 修改索引的值,只有被删除的值不是根节点时,才需要这个操作
// 此时键值为bigger的元素不需要修改索引,但是小于bigger的元素需要
if(flag){
indexedBinarySearchTreeNode<pair<K, E> > *temp = root;
while (temp != nullptr) {
pp = temp;
cout << *temp << endl;
// 如果当前键值小于temp的键值,则移到temp的左孩子
if (bigger < temp->element.first){
pp->leftSize--;
temp = temp->leftChild;
}
else // 如果当前键值小于等于p的键值,则移到p的右孩子
if(bigger > temp->element.first)
temp = temp->rightChild;
else //当前键值等于p的值,则终止
break;
}
}
}
#endif //_33SEARCH_TREE_INDEXEDBINARYSEARCHTREE_H
应用
直方图
问题描述
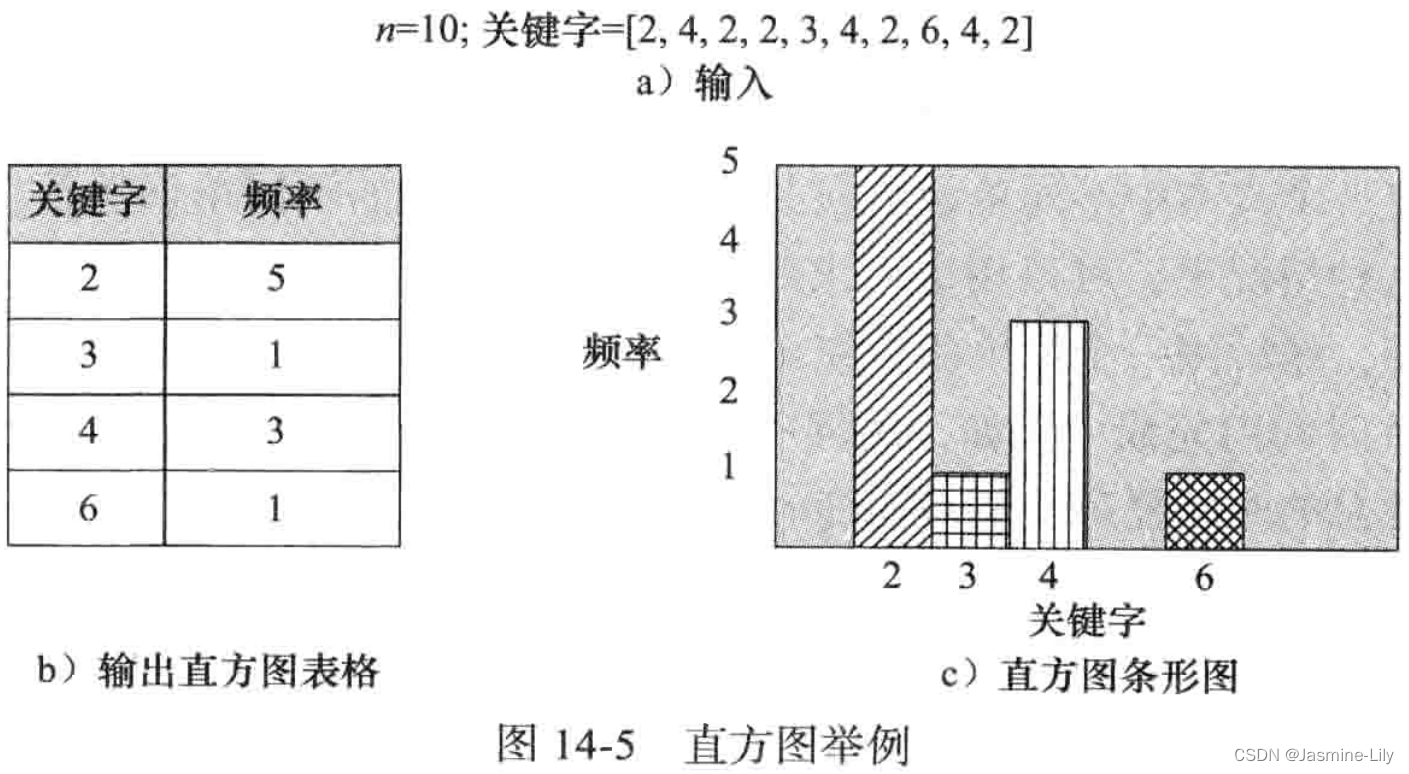
在直方图问题中,输入由n个关键字所构成的集合,然后输出一个列表,它包含不同关键字及其每个关键字在集合中出现的次数(频率)。图14-5是一个含有10个关键字的例子。图14-5a是直方图的输入,图14-5b是直方图的输出表格,图14-5c是直方图的条形图。直方图一般用来确定数据的分布。
简单求解方法
/*
* 直方图的简单求法
* 时间复杂度:O(n),但是当关键字的范围很大时,不再适用
*/
void SimpleHistogramSolution() {
int n, r; // 元素个数,元素的上限
cout << "Enter number of elements and range" << endl;
cin >> n >> r;
// 生成直方图数组h
int *h = new int[r + 1];
// 初始化直方图数组h
for(int i = 0; i <= r; i++)
h[i] = 0;
for (int i = 1; i <= n; i++)
{
int key;// 假设输入的值在0-r之间
cout << "Enter element " << i << endl;
cin >> key;
h[key]++;
}
// 输出直方图
cout << "Distinct elements and frequencies are"
<< endl;
for(int i = 0; i <= r; i++)
if(h[i] != 0)
cout << i << " " << h[i] << endl;
delete [] h;
}
此方法的时间复杂度为O(n),n表示关键字的个数。
当关键字的类型不是整型并且关键字范围很大时,此方法不再适用。
二叉搜索树求解
当关键字的种类m非常小时,可以使用二叉搜索树。
首先需要为binarySearchTree定义新的成员函数:此函数在插入元素{key, num}时,如原树中存在键值为的节点,则将搜索到的该节点的num++;反之,将新元素插入二叉搜素树。
void insert(const pair<K, E>&, void(*fun)(E& u));
测试函数为:
void add(int& count) {count++;}
/*
* 直方图的二叉搜索树求法
* 时间复杂度:O(nlog(m)),n表示输入关键字个数,m表示关键字有多少种
* 当m很小时,此方法非常好用
*/
void binarySearchTreeHistogramSolution() {
int n; // 元素个数
cout << "Enter number of elements" << endl;
cin >> n;
// 输入元素并插入到二叉搜索树中
binarySearchTree<int, int> theTree;
for (int i = 1; i <= n; i++)
{
pair<int, int> thePair; // 输入元素
cout << "Enter element " << i << endl;
cin >> thePair.first; // 键值
thePair.second = 1; // 频率
// 将这一对插入到树中,除非匹配已经存在,在后一种情况下对应的键值增加1
theTree.insert(thePair, add);
}
// 输出直方图
cout << "Distinct elements and frequencies are"
<< endl;
theTree.ascend();
}
箱子装载问题的最优适配法
使用有重复值的二叉搜索树实现的
见链接:地址
交叉分布
通道布线与交叉
在交叉分布问题中,从一个布线通道开始,在通道的顶部和底部各有n个针脚。图14-7是一个n=10的实例。布线区域是带阴影的长方形区域。在通道的顶部和底部,针脚从左至右,从1到n编号。另外,对[1,2,3,,]的一个排列C,用一条线路将顶部的针脚i与底部的针脚 C i C_i Ci连接起来。在图14-7的实例中:C=[8,7,4,2,5,1,9,3,10,6]。实现这些连接的n条线路从1到n编号。线路i连接顶部的针脚i和底部的针脚 C i C_i Ci。当且仅当i<j时,线路i在线路j的左边。
在图14-7的布线区域中,无论线路9和10如何布设,它们一定会在某一点交叉。每个交叉用一个数对(i,j)表示,其中i和j是两条交叉的线路。为了避免一个交叉提及两次,我们要求i<j(注意,交叉(10,9)和(9,10)是一样的)。注意,线路i和j交叉(i<j),当且仅当 C i > C j C_i>C_j Ci>Cj。令 k i k_i ki,表示这种数对(i,j)的数量。在图14-7中, k 9 = 1 , k 10 = 0 k_9=1,k_{10}=0 k9=1,k10=0。图14-8列出了图14-7的所有交叉及 k i k_i ki的值。表的第i行首先是 k i k_i ki的值,然后是j的值,其中i<j,线路i与j相交。交叉的总数K是所有 k i k_i ki的和。在本例中,K=22。
分布交叉
为了使通道的上半部和下半部的布线平衡,我们要求每一部分含有数量大致相同的交叉(上半部应该有 ⌊ K / 2 ⌋ \lfloor K/2\rfloor ⌊K/2⌋次交叉,下半部应该有 ⌊ K / 2 ⌋ \lfloor K/2\rfloor ⌊K/2⌋次交叉)。图14-9是图14-7的一种布线,每一部分大约有11个交叉。
上半部分的连接由排列A=[1,4,6,3,7,2,9,5,10,8]给出,即顶部的针脚i与中间的针脚 A i A_i Ai连接。下半部分的连接由排列B=[8,1,2,7,3,4,5,6,9,10]给出,中间的针脚i与底部的针脚 B i B_i Bi连接。可以看出 C i = B A i , 1 ≤ i ≤ n C_i = B_{A_i},1\leq i \leq n Ci=BAi,1≤i≤n,为了实现均匀分布交叉,满足这个等式是必要的。需要设计一个算法,计算排列A和B,使得上半部有 ⌊ K / 2 ⌋ \lfloor K/2\rfloor ⌊K/2⌋次交叉,下半部有 ⌊ K / 2 ⌋ \lfloor K/2\rfloor ⌊K/2⌋次交叉,其中K是交叉总数。
使用线性表实现分布交叉
代码:
/*
* 交叉分布的简单求法
* 不太看得明白
* 时间复杂度:O(n^2)
*/
[[noreturn]] void SimpleCrossDistribution() {
// 定义要解决的问题实例
// 在通道底部的连接点theC[1:10]
int theC[] = {0, 8, 7, 4, 2, 5, 1, 9, 3, 10, 6};
// 交叉数量k[1:10]
int k[] = {0, 7,6,3,1,2,0,2,0,1,0};
int n = 10;// 在通道每一边的针脚数量
int theK = 22;// 交叉总数量
// 生成数据结构
std::vector<int> theList(n);
int * theA = new int[n + 1];// 顶端的排列
int * theB = new int[n + 1];// 底端的排列
int * theX = new int[n + 1];// 中间的排列:表明哪一条线路连接到中间的针脚上
// 需要在上半部分保留的交叉数
int crossingsNeeded = theK / 2;
// 从右到左扫描线路
// 如果将与cur相交的k[cur]条线路中的c条分配到上半部分,那么这条线路必定与theList中的前c条线路相交。
int currentWire = n;
while(currentWire > 0){
if(k[currentWire] < crossingsNeeded){
// 使用来自cur的所有交叉
theList.insert(theList.begin() + k[currentWire], currentWire);
crossingsNeeded -= k[currentWire];
}
else{
// 仅使用来自cur的crossingsNeeded
theList.insert(theList.begin() + crossingsNeeded, currentWire);
crossingsNeeded = 0;
}
currentWire--;
}
// 确定中间的线路排列
// 前面这一段的交叉放到下半部,因此连接到自己平行的地方就行
for(int i = 1; i <= currentWire; i++)
theX[i] = i;
// 剩余线路次序来自表,theX表示哪一条线路连接到中间的针脚上
for(int i = currentWire + 1; i <= n; i++)
theX[i] = theList[i - currentWire - 1];
// 计算上半部的排列
for(int i = 1; i <= n; i++)
theA[theX[i]] = i;
// 计算下半部的排列
for(int i = 1; i <= n; i++)
theB[i] = theC[theX[i]];
cout << "A is ";
for(int i = 1; i <= n; i++)
cout << theA[i] << " ";
cout << endl;
cout << "B is ";
for(int i = 1; i <= n; i++)
cout << theB[i] << " ";
cout << endl;
delete [] theA;
delete [] theB;
delete [] theX;
}
举例:
下面根据图14-7的列子来建立theX。先将线路10插入theList,得到 theList=(10)。没有产生交叉。接下来把线路9插入theList,得到theList=(10,9)。这时在上半部分产生了1个交叉。然后将8插入第 k 8 k_8 k8个元素后边,得到theList=(8,10,9)。此时在上部分的右边交叉总数仍然是1。将7插入第二个元素之后,上半部分有2个交叉,theList变为(8,10,7,9),所需的相交次数r下降到8。当6插入后,得到theList=(6,8,10,7,9),r=8。线路5插人后产生2个交叉,theList=(6,8,5,10,7,9),r=6。线路4插入首元素之后产生一个交叉,theList=(6,4,8,5,10,7,9),r=5。线路3插入后,得到 theList=(6,4,8,3,5,10,7,9),r=2。最后考虑线路2。虽然它能产生k2=6个交叉,但只能将其中2个分配到通道的上半部分,因此它被插入 theList第二个元素的右边,得到theList=(6,4,2,8,3,5,10,7,9)。
剩下的路线保持它们的相对次序。
在完成上半部分的布线之后,计算线路的排列,通过在序列(1,2,…,w)上附加theList得到 theX=[1,6,4,2,8,3,5,10,7,9]。
排列 theA=A与 theX关系密切。theA[i]表明线路j应该连接到中间的哪个针脚上,而 theX[i]表明哪一条线路连接到中间的针脚上。上述程序的第三个for循环就是用这种信息来计算theA的。如同在第四个for循环中一样,利用 theX 和 theC 计算出 theB=B。
使用索引二叉树
看不懂,但是这个地方属于是索引二叉树的应用了,自己没有想到索引二叉树的应用。后面需要再来看一下这个题目,好好想想。
完整测试代码
main.cpp
/*
Project name : _33Search_tree
Last modified Date: 2023年12月21日11点13分
Last Version: V1.0
Descriptions: 二叉搜索树——main函数
*/
#include "binarySearchTree.h"
#include "dBinarySearchTree.h"
#include "indexedBinarySearchTree.h"
using namespace std;
int main(void)
{
// 测试二叉搜索树
binarySearchTreeTest();
// 测试带有相同关键字的二叉搜索树
dBinarySearchTreeTest();
// 测试索引二叉树
indexedBinarySearchTreeTest();
// 搜索二叉树的应用
// 直方图 简单求解
SimpleHistogramSolution();
// 直方图的二叉搜索树求解
binarySearchTreeHistogramSolution();
// 分布交叉 简单求解
SimpleCrossDistribution();
}
binarySearchTree.h
/*
Project name : _33Search_tree
Last modified Date: 2023年12月21日11点13分
Last Version: V1.0
Descriptions: 二叉搜索树——模板类实现
*/
#ifndef _33SEARCH_TREE_BINARYSEARCHTREE_H
#define _33SEARCH_TREE_BINARYSEARCHTREE_H
#include "bsTree.h"
#include "binaryTreeNode.h"
using namespace std;
void binarySearchTreeTest();
/*二叉搜索树的应用*/
/*直方图*/
void SimpleHistogramSolution();
void binarySearchTreeHistogramSolution();
/*分布交叉*/
void SimpleCrossDistribution();
template<class K, class E>
class binarySearchTree : public bsTree<K,E>
{
public:
binarySearchTree(){
root = nullptr;
treeSize = 0;
}
// 字典相关的方法
bool empty() const {return treeSize == 0;}
int size() const {return treeSize;}
pair<K, E>* find(const K theKey) const;
void insert(const pair<K, E> thePair);
void insert(const pair<K, E>&, void(*fun)(E& u));// 这是为了求解直方图所作的努力
void erase(const K theKey);
/*中序遍历二叉树,使用函数指针的目的是是的本函数可以实现多种目的*/
void inOrder(void(*theVisit)(binaryTreeNode<pair<K, E>>*))
{
visit = theVisit;
/*是因为递归,所以才要这样的*/
inOrder(root);/*这里调用的是静态成员函数inOrder()*/
}
/*中序遍历---输出endl*/
void inOrderOutput() { inOrder(output); cout << endl; }
// additional method of bsTree
void ascend() {inOrderOutput();}
private:
binaryTreeNode<pair<K, E>>* root;//指向根的指针
int treeSize;//树的结点个数
static void (*visit)(binaryTreeNode<pair<K, E>>*);//是一个函数指针,返回值为void 函数参数为binaryTreeNode<pair<K, E>>*
static void output(binaryTreeNode<pair<K, E>>* t) { cout << t->element << " "; }
static void inOrder(binaryTreeNode<pair<K, E>>* t);
};
/*私有静态成员初始化*/
/*这里是静态函数指针成员的初始化,不初始化会引发LINK错误*/
template<class K, class E>
void (*binarySearchTree<K,E>::visit)(binaryTreeNode<pair<K, E>>*) = 0; // visit function
/*中序遍历 递归*/
template<class K, class E>
void binarySearchTree<K,E>::inOrder(binaryTreeNode<pair<K, E>>* t)
{
if (t != nullptr)
{
inOrder(t->leftChild);/*中序遍历左子树*/
visit(t);/*访问树根*/
inOrder(t->rightChild);/*中序遍历右子树*/
}
}
/* 查找元素
* 输入:theKey表示需要查找元素的键值
* 输出:键值为theKey的节点的pair地址
* 时间复杂度:O(logn),n表示节点个数
*/
template<class K, class E>
pair<K, E>* binarySearchTree<K,E>::find(K theKey) const
{
// 返回值是匹配数对的指针
// 如果没有匹配的数对,返回值为nullptr
// p从根节点开始搜索,寻找关键字等于theKey的一个元素
binaryTreeNode<pair<K, E> > *p = root;
while (p != nullptr)
// 检查元素 p->element
if (theKey < p->element.first)
p = p->leftChild;
else
if (theKey > p->element.first)
p = p->rightChild;
else // 找到匹配的元素
return &p->element;
// 没找到匹配的元素
return nullptr;
}
/*
* 插入元素
* 输入:const pair<K, E> thePair表示需要插入的键值对
* 输出:void
* 时间复杂度:O(logn),表示节点个数
*/
template<class K, class E>
void binarySearchTree<K,E>::insert(const pair<K, E> thePair)
{
// 插入thePair. 如果该键值存在则覆盖元素
// 寻找插入位置
binaryTreeNode<pair<K, E> > *p = root,
*pp = nullptr;
while (p != nullptr)
{// 检查元素 p->element
pp = p;
// 如果当前键值小于p的键值,则移到p的左孩子
if (thePair.first < p->element.first)
p = p->leftChild;
else// 如果当前键值大于p的键值,则移到p的右孩子
if (thePair.first > p->element.first)
p = p->rightChild;
else
{// 如果键值相等,覆盖旧的值
p->element.second = thePair.second;
return;
}
}
// 为thePair建立一个节点,然后与pp链接,此时pp是叶子节点
auto *newNode = new binaryTreeNode<pair<K, E> > (thePair);
if (root != nullptr) // 树非空
// 如果thePair的键值小于pp的键值,则将thePair作为pp的左孩子,反之将其作为右孩子
if (thePair.first < pp->element.first)
pp->leftChild = newNode;
else
pp->rightChild = newNode;
else// 树空
root = newNode; // 直接将thePair节点作为根节点
treeSize++;
}
/*
* 插入元素
* 输入:const pair<K, E> thePair表示需要插入的键值对
* 输出:void
* 时间复杂度:O(logn),表示节点个数
* 目的:为了应用于直方图求解所作的努力
*/
template<class K, class E>
void binarySearchTree<K,E>::insert(const pair<K, E>& thePair, void(*fun)(E& u))
{
// 插入thePair. 如果该键值存在则覆盖元素
// 寻找插入位置
binaryTreeNode<pair<K, E> > *p = root,
*pp = 0; // p的父亲节点
while (p != nullptr)
{
pp = p;
// 移到p的孩子节点
if (thePair.first < p->element.first)
p = p->leftChild;
else
if (thePair.first > p->element.first)
p = p->rightChild;
else
{// 访问这个元素
fun(p->element.second);
return;
}
}
// 为thePair建立一个节点,然后与pp链接,此时pp是叶子节点
auto *newNode = new binaryTreeNode<pair<K, E> > (thePair);
if (root != nullptr) // 不是空树
if (thePair.first < pp->element.first)
pp->leftChild = newNode;
else
pp->rightChild = newNode;
else
root = newNode; // 是空树
treeSize++;
}
/*
* 删除元素
* 输入:const K theKey表示需要删除元素的键值
* 输出:void
* 时间复杂度:O(logn),n表示节点个数
*/
template<class K, class E>
void binarySearchTree<K,E>::erase(const K theKey)
{
// 删除关键字等于theKey的数对
// 查找关键字为theKey的节点
binaryTreeNode<pair<K, E> > *p = root,
*pp = nullptr;
while (p != nullptr && p->element.first != theKey)
{
pp = p;
if (theKey < p->element.first)
p = p->leftChild;
else
p = p->rightChild;
}
if (p == nullptr)
return; // 不存在与关键字theKey匹配的数对
// 重新组织树结构
// 当p有两个孩子时的处理
if (p->leftChild != nullptr && p->rightChild != nullptr)
{
// 两个孩子
// 在P的左子树中寻找最大元素
binaryTreeNode<pair<K, E> > *s = p->leftChild,
*ps = p; // s的父节点
while (s->rightChild != nullptr)
{// 移动到更大的pair
ps = s;
s = s->rightChild;// 右孩子比较大
}
// 将最大元素s移到p
// p->element = s->element 的键值是 const
// 当最大值就是p的左孩子时,new的元素不能直接指向p的左孩子,而要指向p的左孩子的左孩子(此时p的左孩子没有右孩子),因为到时候s会被delete掉,这个问题在后面的p至多有一个孩子那里解决的
binaryTreeNode<pair<K, E> >* q = nullptr;
q = new binaryTreeNode<pair<K, E> >(s->element, p->leftChild, p->rightChild);
// pp是p的父节点
// 如果p没有父节点
if (pp == nullptr)
root = q;
else if (p == pp->leftChild)// 如果p是pp的左孩子
pp->leftChild = q;
else// 如果p是pp的右孩子
pp->rightChild = q;
// 如果s的父节点就是p,说明p节点的左子树只有左子树没有右子树
// 那么删除p后pp就是其父节点
if (ps == p) pp = q;
else pp = ps;// 反之ps是其父节点
delete p;
p = s;
}
// p至多只有一个孩子
// 把孩子的指针存放到c
binaryTreeNode<pair<K, E> > *c;
if (p->leftChild != nullptr)
c = p->leftChild;
else
c = p->rightChild;
// 删除p
if (p == root)
root = c;
else
{// p是pp的左孩子还是右孩子
if (p == pp->leftChild)
pp->leftChild = c;
else pp->rightChild = c;
}
treeSize--;
delete p;
}
// overload << for pair
template <class K, class E>
ostream& operator<<(ostream& out, const pair<K, E>& x)
{out << x.first << ":" << x.second; return out;}
#endif //_33SEARCH_TREE_BINARYSEARCHTREE_H
dBinarySearchTree.h
/*
Project name : _33Search_tree
Last modified Date: 2023年12月21日11点13分
Last Version: V1.0
Descriptions: 二叉搜索树——带有相同关键字的二叉搜索树模板类
*/
#ifndef _33SEARCH_TREE_DBINARYSEARCHTREE_H
#define _33SEARCH_TREE_DBINARYSEARCHTREE_H
#include "bsTree.h"
#include "binaryTreeNode.h"
using namespace std;
void dBinarySearchTreeTest();
template<class K, class E>
class dBinarySearchTree : public bsTree<K,E>
{
public:
dBinarySearchTree(){
root = nullptr;
treeSize = 0;
}
// 字典相关的方法
bool empty() const {return treeSize == 0;}
int size() const {return treeSize;}
pair<K, E>* find(const K theKey) const;
pair<K, E>* findGE(const K theKey) const;
void insert(const pair<K, E> thePair);
void erase(const K theKey);
/*中序遍历二叉树,使用函数指针的目的是是的本函数可以实现多种目的*/
void inOrder(void(*theVisit)(binaryTreeNode<pair<K, E>>*))
{
visit = theVisit;
/*是因为递归,所以才要这样的*/
inOrder(root);/*这里调用的是静态成员函数inOrder()*/
}
/*中序遍历---输出endl*/
void inOrderOutput() { inOrder(output); cout << endl; }
// additional method of bsTree
void ascend() {inOrderOutput();}
private:
binaryTreeNode<pair<K, E>>* root;//指向根的指针
int treeSize;//树的结点个数
static void (*visit)(binaryTreeNode<pair<K, E>>*);//是一个函数指针,返回值为void 函数参数为binaryTreeNode<pair<K, E>>*
static void output(binaryTreeNode<pair<K, E>>* t) { cout << t->element << " "; }
static void inOrder(binaryTreeNode<pair<K, E>>* t);
};
/*私有静态成员初始化*/
/*这里是静态函数指针成员的初始化,不初始化会引发LINK错误*/
template<class K, class E>
void (*dBinarySearchTree<K,E>::visit)(binaryTreeNode<pair<K, E>>*) = 0; // visit function
/*中序遍历 递归*/
template<class K, class E>
void dBinarySearchTree<K,E>::inOrder(binaryTreeNode<pair<K, E>>* t)
{
if (t != nullptr)
{
inOrder(t->leftChild);/*中序遍历左子树*/
visit(t);/*访问树根*/
inOrder(t->rightChild);/*中序遍历右子树*/
}
}
/* 查找元素
* 输入:theKey表示需要查找元素的键值
* 输出:键值为theKey的节点的pair地址
* 时间复杂度:O(logn),n表示节点个数
*/
template<class K, class E>
pair<K, E>* dBinarySearchTree<K,E>::find(K theKey) const
{
// 返回值是匹配数对的指针
// 如果没有匹配的数对,返回值为nullptr
// p从根节点开始搜索,寻找关键字等于theKey的一个元素
binaryTreeNode<pair<K, E> > *p = root;
while (p != nullptr)
// 检查元素 p->element
if (theKey < p->element.first)
p = p->leftChild;
else
if (theKey > p->element.first)
p = p->rightChild;
else // 找到匹配的元素
return &p->element;
// 没找到匹配的元素
return nullptr;
}
/* 查找元素,目的是解决箱子装载问题的最有匹配方法,将element.first作为箱子的容量,element.second作为箱子的名称
* 输入:theKey表示需要查找元素的键值
* 输出:返回值是剩余容量即大于等于theKey又是最小的箱子的element的地址
* 时间复杂度:O(logn),n表示节点个数
*/
template<class K, class E>
pair<K, E>* dBinarySearchTree<K,E>::findGE(const K theKey) const{
// 返回一个元素的指针,这个元素的关键字是不小于theKey的最小关键字
// 如果这样的元素不存在,返回NULL
binaryTreeNode<pair<K, E>> * cur = root;
// 目前找到的元素,其关键字是不小于theKey的最小关键字
pair<K, E> * bestBin = nullptr;
// 对树搜索
while(cur != nullptr){
// cur是一个候选者吗
if(cur->element.first >= theKey) // 是比bestBin更好的候选者
{
bestBin = &cur->element;
cur = cur->leftChild;// 再往左子树去找
}
else // 不是
cur = cur->rightChild;// 再往右子树去找
}
return bestBin;
}
/*
* 插入元素
* 输入:const pair<K, E> thePair表示需要插入的键值对
* 输出:void
* 时间复杂度:O(logn),表示节点个数
*/
template<class K, class E>
void dBinarySearchTree<K,E>::insert(const pair<K, E> thePair)
{
// 插入thePair. 如果该键值存在则覆盖元素
// 寻找插入位置
binaryTreeNode<pair<K, E> > *p = root,
*pp = nullptr;
while (p != nullptr)
{// 检查元素 p->element
pp = p;
// 如果当前键值小于等于p的键值,则移到p的左孩子
if (thePair.first <= p->element.first)
p = p->leftChild;
else// 如果当前键值大于p的键值,则移到p的右孩子
p = p->rightChild;
}
// 为thePair建立一个节点,然后与pp链接,此时pp是叶子节点
auto *newNode = new binaryTreeNode<pair<K, E> > (thePair);
if (root != nullptr) // 树非空
// 如果thePair的键值小于pp的键值,则将thePair作为pp的左孩子,反之将其作为右孩子
if (thePair.first < pp->element.first)
pp->leftChild = newNode;
else
pp->rightChild = newNode;
else// 树空
root = newNode; // 直接将thePair节点作为根节点
treeSize++;
}
/*
* 删除元素
* 输入:const K theKey表示需要删除元素的键值
* 输出:void
* 时间复杂度:O(logn),n表示节点个数
*/
template<class K, class E>
void dBinarySearchTree<K,E>::erase(const K theKey)
{
// 删除关键字等于theKey的数对
// 查找关键字为theKey的节点
binaryTreeNode<pair<K, E> > *p = root,
*pp = nullptr;
while (p != nullptr && p->element.first != theKey)
{
pp = p;
if (theKey < p->element.first)
p = p->leftChild;
else
p = p->rightChild;
}
if (p == nullptr)
return; // 不存在与关键字theKey匹配的数对
// 重新组织树结构
// 当p有两个孩子时的处理
if (p->leftChild != nullptr && p->rightChild != nullptr)
{
// 两个孩子
// 在P的左子树中寻找最大元素
binaryTreeNode<pair<K, E> > *s = p->leftChild,
*ps = p; // s的父节点
while (s->rightChild != nullptr)
{// 移动到更大的pair
ps = s;
s = s->rightChild;// 右孩子比较大
}
// 将最大元素s移到p
// p->element = s->element 的键值是 const
// 当最大值就是p的左孩子时,new的元素不能直接指向p的左孩子,而要指向p的左孩子的左孩子(此时p的左孩子没有右孩子),因为到时候s会被delete掉,这个问题在后面的p至多有一个孩子那里解决的
binaryTreeNode<pair<K, E> >* q = nullptr;
q = new binaryTreeNode<pair<K, E> >(s->element, p->leftChild, p->rightChild);
// pp是p的父节点
// 如果p没有父节点
if (pp == nullptr)
root = q;
else if (p == pp->leftChild)// 如果p是pp的左孩子
pp->leftChild = q;
else// 如果p是pp的右孩子
pp->rightChild = q;
// 如果s的父节点就是p,说明p节点的左子树只有左子树没有右子树
// 那么删除p后pp就是其父节点
if (ps == p) pp = q;
else pp = ps;// 反之ps是其父节点
delete p;
p = s;
}
// p至多只有一个孩子
// 把孩子的指针存放到c
binaryTreeNode<pair<K, E> > *c;
if (p->leftChild != nullptr)
c = p->leftChild;
else
c = p->rightChild;
// 删除p
if (p == root)
root = c;
else
{// p是pp的左孩子还是右孩子
if (p == pp->leftChild)
pp->leftChild = c;
else pp->rightChild = c;
}
treeSize--;
delete p;
}
#endif //_33SEARCH_TREE_DBINARYSEARCHTREE_H
indexedBinarySearchTree.h
/*
Project name : _33Search_tree
Last modified Date: 2023年12月21日11点13分
Last Version: V1.0
Descriptions: 二叉搜索树——索引二叉树的模板类
*/
#ifndef _33SEARCH_TREE_INDEXEDBINARYSEARCHTREE_H
#define _33SEARCH_TREE_INDEXEDBINARYSEARCHTREE_H
#include "indexedBSTree.h"
#include "indexedBinarySearchTreeNode.h"
using namespace std;
void indexedBinarySearchTreeTest();
template<class K, class E>
class indexedBinarySearchTree : public indexedBSTree<K, E> {
public:
indexedBinarySearchTree() {
root = nullptr;
treeSize = 0;
}
// 字典相关的方法
[[nodiscard]] bool empty() const { return treeSize == 0; }
[[nodiscard]] int size() const { return treeSize; }
pair<K, E> *find(const K theKey) const;
// index从0开始
[[nodiscard]] pair<K, E>* get(int index) const;
void insert(const pair<K, E> thePair);
void erase(const K theKey);
/*中序遍历二叉树,使用函数指针的目的是是的本函数可以实现多种目的*/
void inOrder(void(*theVisit)(indexedBinarySearchTreeNode<pair<K, E>> *)) {
visit = theVisit;
/*是因为递归,所以才要这样的*/
inOrder(root);/*这里调用的是静态成员函数inOrder()*/
}
/*中序遍历---输出endl*/
void inOrderOutput() {
inOrder(output);
cout << endl;
}
/*前序遍历二叉树,使用函数指针的目的是是的本函数可以实现多种目的*/
void preOrder(void(*theVisit)(indexedBinarySearchTreeNode<pair<K, E>> *))
{
visit = theVisit;
/*是因为递归,所以才要这样的*/
preOrder(root);/*这里调用的是成员函数,preOrder()*/
}
/*前序遍历---输出endl*/
void preOrderOutput() { preOrder(output); cout << endl; }
// additional method of bsTree
void ascend() { inOrderOutput(); }
private:
indexedBinarySearchTreeNode<pair<K, E>> *root;//指向根的指针
int treeSize;//树的结点个数
static void (*visit)(indexedBinarySearchTreeNode<pair<K, E>> *);//是一个函数指针,返回值为void 函数参数为indexedBinarySearchTreeNode<pair<K, E>>
static void output(indexedBinarySearchTreeNode<pair<K, E>> *t) { cout << *t << " "; }
static void inOrder(indexedBinarySearchTreeNode<pair<K, E>> *t);
static void preOrder(indexedBinarySearchTreeNode<pair<K, E>> *t);
};
/*私有静态成员初始化*/
/*这里是静态函数指针成员的初始化,不初始化会引发LINK错误*/
template<class K, class E>
void
(*indexedBinarySearchTree<K, E>::visit)(indexedBinarySearchTreeNode<pair<K, E>> *) = 0; // visit function
/*中序遍历 递归*/
template<class K, class E>
void indexedBinarySearchTree<K, E>::inOrder(indexedBinarySearchTreeNode<pair<K, E>> *t) {
if (t != nullptr) {
inOrder(t->leftChild);/*中序遍历左子树*/
visit(t);/*访问树根*/
inOrder(t->rightChild);/*中序遍历右子树*/
}
}
/*二叉树的普通成员函数*/
/*前序遍历 递归*/
template<class K, class E>
void indexedBinarySearchTree<K, E>::preOrder(indexedBinarySearchTreeNode<pair<K, E>> *t)
{
if (t != nullptr)
{
visit(t);/*访问树根*/
preOrder(t->leftChild);/*前序遍历左子树*/
preOrder(t->rightChild);/*前序遍历右子树*/
}
}
/* 根据键值查找元素
* 输入:theKey表示需要查找元素的键值
* 输出:键值为theKey的节点的pair地址
* 时间复杂度:O(logn),n表示节点个数
*/
template<class K, class E>
pair<K, E> *indexedBinarySearchTree<K, E>::find(K theKey) const {
// 返回值是匹配数对的指针
// 如果没有匹配的数对,返回值为nullptr
// p从根节点开始搜索,寻找关键字等于theKey的一个元素
indexedBinarySearchTreeNode<pair<K, E> > *p = root;
while (p != nullptr)
// 检查元素 p->element
if (theKey < p->element.first)
p = p->leftChild;
else if (theKey > p->element.first)
p = p->rightChild;
else // 找到匹配的元素
return &p->element;
// 没找到匹配的元素
return nullptr;
}
/*
* 根据索引查找元素
* 输入:int index表示查找节点的索引
* 输出:索引为index的节点的pair地址
*/
template<class K, class E>
pair<K, E>* indexedBinarySearchTree<K, E>::get(int index) const {
indexedBinarySearchTreeNode<pair<K, E> >* cur = root;
while(cur != nullptr && cur->leftSize != index){
// 当前节点的索引大于index,移动到左孩子
if(cur->leftSize > index)
cur = cur->leftChild;
else{// 当前节点的索引小于index,移动到右孩子
index = index - (cur->leftSize + 1);
cur = cur->rightChild;
}
}
if(cur == nullptr)
return nullptr;
else
return &(cur->element);
}
/*
* 插入元素
* 输入:const pair<K, E> thePair表示需要插入的键值对
* 输出:void
* 时间复杂度:O(logn),表示节点个数
*/
template<class K, class E>
void indexedBinarySearchTree<K, E>::insert(const pair<K, E> thePair) {
// 插入thePair. 如果该键值存在则覆盖元素
// 寻找插入位置
indexedBinarySearchTreeNode<pair<K, E> > *p = root,
*pp = nullptr;
while (p != nullptr) {// 检查元素 p->element
pp = p;
// 如果当前键值小于p的键值,则移到p的左孩子
if (thePair.first < p->element.first)
p = p->leftChild;
else// 如果当前键值大于p的键值,则移到p的右孩子
if (thePair.first > p->element.first)
p = p->rightChild;
else {// 如果键值相等,覆盖旧的值
p->element.second = thePair.second;
return;
}
}
// 为thePair建立一个节点,然后与pp链接,此时pp是叶子节点
auto *newNode = new indexedBinarySearchTreeNode<pair<K, E> >(thePair);
if (root != nullptr) // 树非空
// 如果thePair的键值小于pp的键值,则将thePair作为pp的左孩子,反之将其作为右孩子
if (thePair.first < pp->element.first) {
pp->leftChild = newNode;// pp的左孩子指向插入的元素,因此pp的索引要更改为1
} else
pp->rightChild = newNode;
else// 树空
root = newNode; // 直接将thePair节点作为根节点
treeSize++;
// 修改索引的值,此时刚加入的元素的leftSize需要调整
p = root;
while (p != nullptr) {// 检查元素 p->element
pp = p;
// 如果当前键值小于p的键值,则移到p的左孩子
if (thePair.first < p->element.first){
pp->leftSize++;
p = p->leftChild;
}
else // 如果当前键值小于等于p的键值,则移到p的右孩子
p = p->rightChild;
}
}
/*
* 删除元素
* 输入:const K theKey表示需要删除元素的键值
* 输出:void
* 时间复杂度:O(logn),n表示节点个数
*/
template<class K, class E>
void indexedBinarySearchTree<K, E>::erase(const K theKey) {
// 删除关键字等于theKey的数对
// 查找关键字为theKey的节点
indexedBinarySearchTreeNode<pair<K, E> > *p = root,
*pp = nullptr;
bool flag = false; // 用来记录是否需要重新组织索引
while (p != nullptr && p->element.first != theKey) {
pp = p;
if (theKey < p->element.first)
p = p->leftChild;
else
p = p->rightChild;
}
if (p == nullptr)
return; // 不存在与关键字theKey匹配的数对
// 如果删除节点就是根节点,则其他节点的索引无需改变
if(p != root)
flag = true;
// bigger存储比p大的最小的键值,后面用于删除元素后索引的更新
K bigger = p->element.first;
if(pp != nullptr){
if(p == pp->leftChild){
if(p->rightChild == nullptr)
bigger = pp->element.first;
else
bigger = p->rightChild->element.first;
}
else if(p->rightChild != nullptr)
bigger = p->rightChild->element.first;
else
bigger = p->element.first;// 此时记录为p的键值的目的是不更新p的右孩子的索引
}
cout << "bigger = " << bigger << endl;
// 重新组织树结构
// 当p有两个孩子时的处理
if (p->leftChild != nullptr && p->rightChild != nullptr) {
// 两个孩子
// 在P的左子树中寻找最大元素
indexedBinarySearchTreeNode<pair<K, E> > *s = p->leftChild,
*ps = p; // s的父节点
while (s->rightChild != nullptr) {// 移动到更大的pair
ps = s;
s = s->rightChild;// 右孩子比较大
}
// 将最大元素s移到p
// p->element = s->element 的键值是 const
// 当最大值就是p的左孩子时,new的元素不能直接指向p的左孩子,而要指向p的左孩子的左孩子(此时p的左孩子没有右孩子),因为到时候s会被delete掉,这个问题在后面的p至多有一个孩子那里解决的
indexedBinarySearchTreeNode<pair<K, E> > *q = nullptr;
q = new indexedBinarySearchTreeNode<pair<K, E> >(s->element, s->leftSize, p->leftChild, p->rightChild);
// pp是p的父节点
// 如果p没有父节点
if (pp == nullptr)
root = q;
else if (p == pp->leftChild)// 如果p是pp的左孩子
pp->leftChild = q;
else// 如果p是pp的右孩子
pp->rightChild = q;
// 如果s的父节点就是p,说明p节点的左子树只有左子树没有右子树
// 那么删除p后pp就是其父节点
if (ps == p) pp = q;
else pp = ps;// 反之ps是其父节点
delete p;
p = s;
}
// p至多只有一个孩子
// 把孩子的指针存放到c
indexedBinarySearchTreeNode<pair<K, E> > *c;
if (p->leftChild != nullptr)
c = p->leftChild;
else
c = p->rightChild;
// 删除p
if (p == root)
root = c;
else {// p是pp的左孩子还是右孩子
if (p == pp->leftChild)
pp->leftChild = c;
else pp->rightChild = c;
}
treeSize--;
delete p;
// 修改索引的值,只有被删除的值不是根节点时,才需要这个操作
// 此时键值为bigger的元素不需要修改索引,但是小于bigger的元素需要
if(flag){
indexedBinarySearchTreeNode<pair<K, E> > *temp = root;
while (temp != nullptr) {
pp = temp;
cout << *temp << endl;
// 如果当前键值小于temp的键值,则移到temp的左孩子
if (bigger < temp->element.first){
pp->leftSize--;
temp = temp->leftChild;
}
else // 如果当前键值小于等于p的键值,则移到p的右孩子
if(bigger > temp->element.first)
temp = temp->rightChild;
else //当前键值等于p的值,则终止
break;
}
}
}
#endif //_33SEARCH_TREE_INDEXEDBINARYSEARCHTREE_H
binaryTreeNode.h
/*
Project name : allAlgorithmsTest
Last modified Date: 2022年8月27日09点44分
Last Version: V1.0
Descriptions: 二叉树的结点结构体
*/
#pragma once
#ifndef _BINARYTREENODE_H_
#define _BINARYTREENODE_H_
template <class T>
struct binaryTreeNode
{
T element;
binaryTreeNode<T> *leftChild, // left subtree
*rightChild; // right subtree
binaryTreeNode() {leftChild = rightChild = nullptr;}
explicit binaryTreeNode(const T& theElement):element(theElement)
{
leftChild = rightChild = nullptr;
}
binaryTreeNode(const T& theElement,
binaryTreeNode *theLeftChild,
binaryTreeNode *theRightChild)
:element(theElement)
{
leftChild = theLeftChild;
rightChild = theRightChild;
}
};
#endif
bsTree.h
/*
Project name : _33Search_tree
Last modified Date: 2023年12月21日11点13分
Last Version: V1.0
Descriptions: 二叉搜索树——虚基类
*/
#ifndef _33SEARCH_TREE_BSTREE_H
#define _33SEARCH_TREE_BSTREE_H
#include "dictionary.h"
using namespace std;
template<class K, class E>
class bsTree : public dictionary<K,E>
{
public:
virtual void ascend() = 0;
// 按关键字升序输出
};
#endif //_33SEARCH_TREE_BSTREE_H
dictionary.h
/*
Project name : _33Search_tree
Last modified Date: 2023年12月21日11点13分
Last Version: V1.0
Descriptions: 字典虚基类
*/
#ifndef _33SEARCH_TREE_DICTIONARY_H
#define _33SEARCH_TREE_DICTIONARY_H
#include <iostream>
#include <utility>
using namespace std;
template<class K, class E>
class dictionary
{
public:
virtual ~dictionary() = default;
[[nodiscard]] virtual bool empty() const = 0;
// 如果字典为空则返回true,反之返回false
[[nodiscard]] virtual int size() const = 0;
// 返回字典中有多少个pair
virtual pair<K, E>* find(const K) const = 0;
// 根据键值返回pair的指针
virtual void erase(const K) = 0;
// 根据键值移除pair元素
virtual void insert(const pair<K, E>) = 0;
// 插入一个(key, value)pair到字典中
};
#endif //_33SEARCH_TREE_DICTIONARY_H
indexedBinarySearchTreeNode.h
/*
Project name : allAlgorithmsTest
Last modified Date: 2023年12月21日11点28分
Last Version: V1.0
Descriptions: 索引二叉搜索树的结点结构体
*/
#ifndef _33SEARCH_TREE_INDEXEDBINARYSEARCHTREENODE_H
#define _33SEARCH_TREE_INDEXEDBINARYSEARCHTREENODE_H
#include<iostream>
using namespace std;
template<class T>
struct indexedBinarySearchTreeNode {
T element;
int leftSize;
indexedBinarySearchTreeNode<T> *leftChild, // 左子树
*rightChild; // 右子树
indexedBinarySearchTreeNode() { leftChild = rightChild = nullptr; leftSize = 0;}
explicit indexedBinarySearchTreeNode(const T &theElement) : element(theElement) {
leftChild = rightChild = nullptr;
leftSize = 0;
}
indexedBinarySearchTreeNode(const T &theElement,
indexedBinarySearchTreeNode *theLeftChild,
indexedBinarySearchTreeNode *theRightChild)
: element(theElement) {
leftChild = theLeftChild;
rightChild = theRightChild;
leftSize = 0;
}
indexedBinarySearchTreeNode(const T &theElement,
const int theleftSize,
indexedBinarySearchTreeNode *theLeftChild,
indexedBinarySearchTreeNode *theRightChild)
: element(theElement), leftSize(theleftSize) {
leftChild = theLeftChild;
rightChild = theRightChild;
}
};
// overload << for pair
template <class T>
ostream& operator<<(ostream& out, const indexedBinarySearchTreeNode<T>& x)
{
out << x.element << ' ' << x.leftSize;
return out;}
#endif //_33SEARCH_TREE_INDEXEDBINARYSEARCHTREENODE_H
indexedBSTree.h
/*
Project name : _33Search_tree
Last modified Date: 2023年12月21日11点13分
Last Version: V1.0
Descriptions: 索引二叉搜索树虚基类
*/
#ifndef _33SEARCH_TREE_INDEXEDBSTREE_H
#define _33SEARCH_TREE_INDEXEDBSTREE_H
#include "bsTree.h"
template<class K, class E>
class indexedBSTree : public bsTree<K,E>
{
public:
virtual pair<K, E>* get(int index) const = 0;
// 返回第index个数对
};
#endif //_33SEARCH_TREE_INDEXEDBSTREE_H
binarySearchTree.cpp
/*
Project name : _33Search_tree
Last modified Date: 2023年12月21日11点13分
Last Version: V1.0
Descriptions: 二叉搜索树——测试函数汇总
*/
#include "binarySearchTree.h"
#include "dBinarySearchTree.h"
#include "indexedBinarySearchTree.h"
#include<vector>
void binarySearchTreeTest() {
cout << "*************************binarySearchTreeTest() begin*******************************" << endl;
binarySearchTree<int, char> y;
y.insert(pair<int, char>(30, 'a'));
y.insert(pair<int, char>(5, 'b'));
y.insert(pair<int, char>(60, 'c'));
y.insert(pair<int, char>(2, 'd'));
y.insert(pair<int, char>(35, 'e'));
y.insert(pair<int, char>(80, 'f'));
y.insert(pair<int, char>(32, 'g'));
y.insert(pair<int, char>(85, 'h'));
y.insert(pair<int, char>(31, 'i'));
y.insert(pair<int, char>(33, 'j'));
cout << "Tree size is " << y.size() << endl;
cout << "Elements in ascending order are" << endl;
y.ascend();
pair<int, char> *s = y.find(60);
cout << "Search for 60 succeeds " << endl;
cout << s->first << ' ' << s->second << endl;
y.erase(60);
cout << "60 deleted " << endl;
cout << "Tree size is " << y.size() << endl;
cout << "Elements in ascending order are" << endl;
y.ascend();
s = y.find(80);
cout << "Search for 80 succeeds " << endl;
cout << s->first << ' ' << s->second << endl;
y.erase(80);
cout << "80 deleted " << endl;
cout << "Tree size is " << y.size() << endl;
cout << "Elements in ascending order are" << endl;
y.ascend();
s = y.find(30);
cout << "Search for 30 succeeds " << endl;
cout << s->first << ' ' << s->second << endl;
y.erase(30);
cout << "30 deleted " << endl;
cout << "Tree size is " << y.size() << endl;
cout << "Elements in ascending order are" << endl;
y.ascend();
s = y.find(35);
cout << "Search for 35 succeeds " << endl;
cout << s->first << ' ' << s->second << endl;
y.erase(35);
cout << "35 deleted " << endl;
cout << "Tree size is " << y.size() << endl;
cout << "Elements in ascending order are" << endl;
y.ascend();
cout << "***************************binarySearchTreeTest() end*******************************" << endl;
}
void dBinarySearchTreeTest() {
cout << "*************************dBinarySearchTreeTest() begin*******************************" << endl;
dBinarySearchTree<int, char> y;
y.insert(pair<int, char>(30, 'a'));
y.insert(pair<int, char>(5, 'b'));
y.insert(pair<int, char>(60, 'c'));
y.insert(pair<int, char>(30, 'd'));
y.insert(pair<int, char>(35, 'e'));
y.insert(pair<int, char>(80, 'f'));
y.insert(pair<int, char>(32, 'g'));
y.insert(pair<int, char>(30, 'h'));
y.insert(pair<int, char>(31, 'i'));
y.insert(pair<int, char>(33, 'j'));
cout << "Tree size is " << y.size() << endl;
cout << "Elements in ascending order are" << endl;
y.ascend();
pair<int, char> *s = y.find(30);
cout << "Search for 30 succeeds " << endl;
cout << s->first << ' ' << s->second << endl;
y.erase(30);
cout << "30 deleted " << endl;
cout << "Tree size is " << y.size() << endl;
cout << "Elements in ascending order are" << endl;
y.ascend();
s = y.find(30);
cout << "Search for 30 succeeds " << endl;
cout << s->first << ' ' << s->second << endl;
y.erase(30);
cout << "30 deleted " << endl;
cout << "Tree size is " << y.size() << endl;
cout << "Elements in ascending order are" << endl;
y.ascend();
s = y.find(30);
cout << "Search for 30 succeeds " << endl;
cout << s->first << ' ' << s->second << endl;
y.erase(30);
cout << "30 deleted " << endl;
cout << "Tree size is " << y.size() << endl;
cout << "Elements in ascending order are" << endl;
y.ascend();
cout << "***************************dBinarySearchTreeTest() end*******************************" << endl;
}
void indexedBinarySearchTreeTest() {
cout << "*************************indexedBinarySearchTreeTest() begin*******************************" << endl;
indexedBinarySearchTree<int, char> y;
y.insert(pair<int, char>(30, 'a'));
y.insert(pair<int, char>(5, 'b'));
y.insert(pair<int, char>(60, 'c'));
y.insert(pair<int, char>(2, 'd'));
y.insert(pair<int, char>(35, 'e'));
y.insert(pair<int, char>(80, 'f'));
y.insert(pair<int, char>(32, 'g'));
y.insert(pair<int, char>(85, 'h'));
y.insert(pair<int, char>(31, 'i'));
y.insert(pair<int, char>(33, 'j'));
cout << "Tree size is " << y.size() << endl;
cout << "Elements in ascending order are" << endl;
y.ascend();
pair<int, char> *s = y.get(0);
if (s != nullptr)
cout << "get the index " << 0 << " element: " << *s << endl;
s = y.get(1);
if (s != nullptr)
cout << "get the index " << 1 << " element: " << *s << endl;
s = y.get(2);
if (s != nullptr)
cout << "get the index " << 2 << " element: " << *s << endl;
s = y.get(3);
if (s != nullptr)
cout << "get the index " << 3 << " element: " << *s << endl;
s = y.get(4);
if (s != nullptr)
cout << "get the index " << 4 << " element: " << *s << endl;
s = y.get(5);
if (s != nullptr)
cout << "get the index " << 5 << " element: " << *s << endl;
s = y.get(6);
if (s != nullptr)
cout << "get the index " << 6 << " element: " << *s << endl;
s = y.get(7);
if (s != nullptr)
cout << "get the index " << 7 << " element: " << *s << endl;
s = y.get(8);
if (s != nullptr)
cout << "get the index " << 8 << " element: " << *s << endl;
s = y.get(9);
if (s != nullptr)
cout << "get the index " << 9 << " element: " << *s << endl;
s = y.find(30);
cout << "Search for 30 succeeds " << endl;
cout << s->first << ' ' << s->second << endl;
y.erase(30);
cout << "30 deleted " << endl;
cout << "Tree size is " << y.size() << endl;
cout << "Elements in ascending order are" << endl;
y.ascend();
s = y.find(60);
cout << "Search for 60 succeeds " << endl;
cout << s->first << ' ' << s->second << endl;
y.erase(60);
cout << "60 deleted " << endl;
cout << "Tree size is " << y.size() << endl;
cout << "Elements in ascending order are" << endl;
y.ascend();
s = y.find(32);
cout << "Search for 32 succeeds " << endl;
cout << s->first << ' ' << s->second << endl;
y.erase(32);
cout << "32 deleted " << endl;
cout << "Tree size is " << y.size() << endl;
cout << "Elements in ascending order are" << endl;
y.ascend();
s = y.find(80);
cout << "Search for 80 succeeds " << endl;
cout << s->first << ' ' << s->second << endl;
y.erase(80);
cout << "80 deleted " << endl;
cout << "Tree size is " << y.size() << endl;
cout << "Elements in ascending order are" << endl;
y.ascend();
s = y.find(31);
cout << "Search for 31 succeeds " << endl;
cout << s->first << ' ' << s->second << endl;
y.erase(31);
cout << "31 deleted " << endl;
cout << "Tree size is " << y.size() << endl;
cout << "Elements in ascending order are" << endl;
y.ascend();
s = y.find(35);
cout << "Search for 35 succeeds " << endl;
cout << s->first << ' ' << s->second << endl;
y.erase(35);
cout << "35 deleted " << endl;
cout << "Tree size is " << y.size() << endl;
cout << "Elements in ascending order are" << endl;
y.ascend();
s = y.find(85);
cout << "Search for 85 succeeds " << endl;
cout << s->first << ' ' << s->second << endl;
y.erase(85);
cout << "85 deleted " << endl;
cout << "Tree size is " << y.size() << endl;
cout << "Elements in ascending order are" << endl;
y.ascend();
s = y.find(5);
cout << "Search for 5 succeeds " << endl;
cout << s->first << ' ' << s->second << endl;
y.erase(5);
cout << "5 deleted " << endl;
cout << "Tree size is " << y.size() << endl;
cout << "Elements in ascending order are" << endl;
y.ascend();
cout << "***************************indexedBinarySearchTreeTest() end*******************************" << endl;
}
/*二叉搜索树的应用*/
/*
* 直方图的简单求法
* 时间复杂度:O(n),但是当关键字不是整型或者范围很大时,不再适用
*/
void SimpleHistogramSolution() {
cout << "***************************SimpleHistogramSolution() begin*******************************" << endl;
int n, r; // 元素个数,元素的上限
cout << "Enter number of elements and range" << endl;
cin >> n >> r;
// 生成直方图数组h
int *h = new int[r + 1];
// 初始化直方图数组h
for (int i = 0; i <= r; i++)
h[i] = 0;
for (int i = 1; i <= n; i++) {
int key;// 假设输入的值在0-r之间
cout << "Enter element " << i << endl;
cin >> key;
h[key]++;
}
// 输出直方图
cout << "Distinct elements and frequencies are"
<< endl;
for (int i = 0; i <= r; i++)
if (h[i] != 0)
cout << i << " " << h[i] << endl;
delete[] h;
cout << "***************************SimpleHistogramSolution() end*******************************" << endl;
}
void add(int &count) { count++; }
/*
* 直方图的二叉搜索树求法
* 时间复杂度:O(nlog(m)),n表示输入关键字个数,m表示关键字有多少种
* 当m很小时,此方法非常好用
*/
void binarySearchTreeHistogramSolution() {
cout << "***************************binarySearchTreeHistogramSolution() begin*******************************" << endl;
int n; // 元素个数
cout << "Enter number of elements" << endl;
cin >> n;
// 输入元素并插入到二叉搜索树中
binarySearchTree<int, int> theTree;
for (int i = 1; i <= n; i++) {
pair<int, int> thePair; // 输入元素
cout << "Enter element " << i << endl;
cin >> thePair.first; // 键值
thePair.second = 1; // 频率
// 将这一对插入到树中,除非匹配已经存在,在后一种情况下对应的键值增加1
theTree.insert(thePair, add);
}
// 输出直方图
cout << "Distinct elements and frequencies are"
<< endl;
theTree.ascend();
cout << "***************************binarySearchTreeHistogramSolution() end*******************************" << endl;
}
/*
* 交叉分布的简单求法
* 不太看得明白,由于学不会,索引二叉树的解法就放弃了
* 时间复杂度:O(n^2)
*/
void SimpleCrossDistribution() {
cout << "***************************SimpleCrossDistribution() begin*******************************" << endl;
// 定义要解决的问题实例
// 在通道底部的连接点theC[1:10]
int theC[] = {0, 8, 7, 4, 2, 5, 1, 9, 3, 10, 6};
// 交叉数量k[1:10]
int k[] = {0, 7,6,3,1,2,0,2,0,1,0};
int n = 10;// 在通道每一边的针脚数量
int theK = 22;// 交叉总数量
// 生成数据结构
std::vector<int> theList(n);
int * theA = new int[n + 1];// 顶端的排列
int * theB = new int[n + 1];// 底端的排列
int * theX = new int[n + 1];// 中间的排列:表明哪一条线路连接到中间的针脚上
// 需要在上半部分保留的交叉数
int crossingsNeeded = theK / 2;
// 从右到左扫描线路
// 如果将与cur相交的k[cur]条线路中的c条分配到上半部分,那么这条线路必定与theList中的前c条线路相交。
int currentWire = n;
while(currentWire > 0){
if(k[currentWire] < crossingsNeeded){
// 使用来自cur的所有交叉
theList.insert(theList.begin() + k[currentWire], currentWire);
crossingsNeeded -= k[currentWire];
}
else{
// 仅使用来自cur的crossingsNeeded
theList.insert(theList.begin() + crossingsNeeded, currentWire);
crossingsNeeded = 0;
}
currentWire--;
}
// 确定中间的线路排列
// 前面这一段的交叉放到下半部,因此连接到自己平行的地方就行
for(int i = 1; i <= currentWire; i++)
theX[i] = i;
// 剩余线路次序来自表,theX表示哪一条线路连接到中间的针脚上
for(int i = currentWire + 1; i <= n; i++)
theX[i] = theList[i - currentWire - 1];
// 计算上半部的排列
for(int i = 1; i <= n; i++)
theA[theX[i]] = i;
// 计算下半部的排列
for(int i = 1; i <= n; i++)
theB[i] = theC[theX[i]];
cout << "A is ";
for(int i = 1; i <= n; i++)
cout << theA[i] << " ";
cout << endl;
cout << "B is ";
for(int i = 1; i <= n; i++)
cout << theB[i] << " ";
cout << endl;
delete [] theA;
delete [] theB;
delete [] theX;
cout << "***************************SimpleCrossDistribution() end*******************************" << endl;
}
运行结果
"C:\Users\15495\Documents\Jasmine\prj\_Algorithm\Data Structures, Algorithms and Applications in C++\_33Search tree\cmake-build-debug\_33Search_tree.exe"
*************************binarySearchTreeTest() begin*******************************
Tree size is 10
Elements in ascending order are
2:d 5:b 30:a 31:i 32:g 33:j 35:e 60:c 80:f 85:h
Search for 60 succeeds
60 c
60 deleted
Tree size is 9
Elements in ascending order are
2:d 5:b 30:a 31:i 32:g 33:j 35:e 80:f 85:h
Search for 80 succeeds
80 f
80 deleted
Tree size is 8
Elements in ascending order are
2:d 5:b 30:a 31:i 32:g 33:j 35:e 85:h
Search for 30 succeeds
30 a
30 deleted
Tree size is 7
Elements in ascending order are
2:d 5:b 31:i 32:g 33:j 35:e 85:h
Search for 35 succeeds
35 e
35 deleted
Tree size is 6
Elements in ascending order are
2:d 5:b 31:i 32:g 33:j 85:h
***************************binarySearchTreeTest() end*******************************
*************************dBinarySearchTreeTest() begin*******************************
Tree size is 10
Elements in ascending order are
5:b 30:d 30:h 30:a 31:i 32:g 33:j 35:e 60:c 80:f
Search for 30 succeeds
30 a
30 deleted
Tree size is 9
Elements in ascending order are
5:b 30:d 30:h 31:i 32:g 33:j 35:e 60:c 80:f
Search for 30 succeeds
30 h
30 deleted
Tree size is 8
Elements in ascending order are
5:b 30:d 31:i 32:g 33:j 35:e 60:c 80:f
Search for 30 succeeds
30 d
30 deleted
Tree size is 7
Elements in ascending order are
5:b 31:i 32:g 33:j 35:e 60:c 80:f
***************************dBinarySearchTreeTest() end*******************************
*************************indexedBinarySearchTreeTest() begin*******************************
Tree size is 10
Elements in ascending order are
2:d 0 5:b 1 30:a 2 31:i 0 32:g 1 33:j 0 35:e 3 60:c 4 80:f 0 85:h 0
get the index 0 element: 2:d
get the index 1 element: 5:b
get the index 2 element: 30:a
get the index 3 element: 31:i
get the index 4 element: 32:g
get the index 5 element: 33:j
get the index 6 element: 35:e
get the index 7 element: 60:c
get the index 8 element: 80:f
get the index 9 element: 85:h
Search for 30 succeeds
30 a
bigger = 30
30 deleted
Tree size is 9
Elements in ascending order are
2:d 0 5:b 1 31:i 0 32:g 1 33:j 0 35:e 3 60:c 4 80:f 0 85:h 0
Search for 60 succeeds
60 c
bigger = 80
5:b 1
35:e 3
80:f 0
60 deleted
Tree size is 8
Elements in ascending order are
2:d 0 5:b 1 31:i 0 32:g 1 33:j 0 35:e 3 80:f 0 85:h 0
Search for 32 succeeds
32 g
bigger = 33
5:b 1
35:e 3
31:i 0
33:j 0
32 deleted
Tree size is 7
Elements in ascending order are
2:d 0 5:b 1 31:i 0 33:j 0 35:e 2 80:f 0 85:h 0
Search for 80 succeeds
80 f
bigger = 85
5:b 1
35:e 2
85:h 0
80 deleted
Tree size is 6
Elements in ascending order are
2:d 0 5:b 1 31:i 0 33:j 0 35:e 2 85:h 0
Search for 31 succeeds
31 i
bigger = 33
5:b 1
35:e 2
33:j 0
31 deleted
Tree size is 5
Elements in ascending order are
2:d 0 5:b 1 33:j 0 35:e 1 85:h 0
Search for 35 succeeds
35 e
bigger = 85
5:b 1
33:j 0
85:h 0
35 deleted
Tree size is 4
Elements in ascending order are
2:d 0 5:b 1 33:j 0 85:h 0
Search for 85 succeeds
85 h
bigger = 85
5:b 1
33:j 0
85 deleted
Tree size is 3
Elements in ascending order are
2:d 0 5:b 1 33:j 0
Search for 5 succeeds
5 b
bigger = 5
5 deleted
Tree size is 2
Elements in ascending order are
2:d 0 33:j 0
***************************indexedBinarySearchTreeTest() end*******************************
***************************SimpleHistogramSolution() begin*******************************
Enter number of elements and range
10 7
Enter element 1
2
Enter element 2
4
Enter element 3
2
Enter element 4
2
Enter element 5
3
Enter element 6
4
Enter element 7
2
Enter element 8
6
Enter element 9
4
Enter element 10
2
Distinct elements and frequencies are
2 5
3 1
4 3
6 1
***************************SimpleHistogramSolution() end*******************************
***************************binarySearchTreeHistogramSolution() begin*******************************
Enter number of elements
10
Enter element 1
2
Enter element 2
4
Enter element 3
2
Enter element 4
2
Enter element 5
3
Enter element 6
4
Enter element 7
2
Enter element 8
6
Enter element 9
4
Enter element 10
2
Distinct elements and frequencies are
2:5 3:1 4:3 6:1
***************************binarySearchTreeHistogramSolution() end*******************************
***************************SimpleCrossDistribution() begin*******************************
A is 1 4 6 3 7 2 9 5 10 8
B is 8 1 2 7 3 4 5 6 9 10
***************************SimpleCrossDistribution() end*******************************
Process finished with exit code 0