在研究大量的数据之中，哪几组数据比较接近的时候（如哪几个城市的消费习惯比较接近）可以选用这个多分类算法。笔者在观看清风的数模教程以后，总结如下要点：

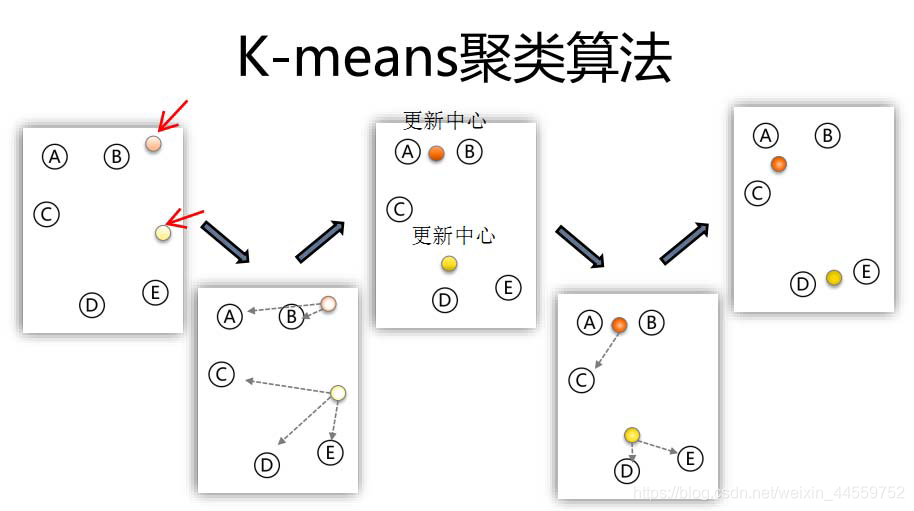
k-means操作流程

1. 选择分类数量k、设置算法的迭代次数
2. 选定初始的k个聚类中心
3. 将所有数据按照距离划分给这k个聚类中心
4. 调整聚类中心的位置（调整为其下所属数据的中心）
5. 重复上述3-4步直到中心位置不再变化或达到迭代次数为止
   
   在实际建模论文中，算法流程描述推荐使用流程图的形式来简化冗余的复述、避免查重

k-means的优缺点

优点

1. 简单、快速
2. 高效处理大数据集

缺点

1. 事先给定的类数k完全由用户指定，过于主观缺乏可靠标准
2. 初值敏感
3. 孤立点敏感

c++代码实现

为了简化距离计算的过程，使用一维的模拟数据：
先看随机初值的三分类效果：

指定初值（低于正常值，高于正常值和正常值三种初值）的分类结果：

代码：

#include<iostream>
#include<vector>
#include<windows.h>
#include<time.h>
using namespace std;
#define random(x) (rand()%x)
#define N 100
vector<double> v;
vector<double> v1, v2, v3;
double abs(double a){
    if(a >=0)
        return a;
    return (-1)*a;
}
void kmeans(){
    double c1 = 1.0*random(100)/10, c2, c3;
    Sleep(1);
    srand((unsigned)clock());
    c2 = 1.0*random(100)/10;
    Sleep(1);
    srand((unsigned)clock());
    c3 = 1.0*random(100)/10;
    cout<<"质心：\n";
    cout<<c1<<' '<<c2<<' '<<c3<<endl;
    int times = 0;//迭代次数
    int tol = 10;//不用太大，几次就能出结果
    while(times++ < tol){
        //分类：
        for(int i = 0; i < v.size(); i++){
            double t1 = abs(c1-v[i]), t2 = abs(c2-v[i]), t3=abs(c3-v[i]);
            if(t1 > t2)
                if(t2 > t3) v3.push_back(v[i]);
                else v2.push_back(v[i]);
            else
                if(t1 > t3) v3.push_back(v[i]);
                else v1.push_back(v[i]);
        }
        double sum = 0;
        for(int i = 0; i < v1.size(); i++)
            sum += v1[i];
        c1 = sum / v1.size();
        sum = 0;
        for(int i = 0; i < v2.size(); i++)
            sum += v2[i];
        c2 = sum / v2.size();
        sum = 0;
        for(int i = 0; i < v3.size(); i++)
            sum += v3[i];
        c3 = sum / v3.size();
        cout<<"质心：\n";
        cout<<c1<<' '<<c2<<' '<<c3<<endl;
        if(times < tol){
            v1.clear();
            v2.clear();
            v3.clear();
        }
    }
}
void printCluster(vector<double> c){
    for(int i = 0; i < c.size(); i++)
        cout<<c[i]<<',';
    cout<<endl;
}
int main()
{
    for(int i = 0; i < N; i++){
        srand((unsigned)clock());
        Sleep(1);
        if(i % 10 == 0){//模拟偏差数据
            v.push_back(10 + (random(200) - 99) / 10.0);
        }
        else{//模拟真实数据
            v.push_back(10 + (random(20) - 9) / 10.0);
        }
    }

    int i = 0;
    while(i++<1){
        kmeans();
        cout<<"第一类\n";
        printCluster(v1);
        cout<<"第二类\n";
        printCluster(v2);
        cout<<"第三类\n";
        printCluster(v3);
    }
	return 0;
}

k-means++：k-means的改进算法

为了尽可能避免上述缺点，提出k-means++算法。

基本原则

选取初始聚类中心的时候，使其间距离尽可能地大

基本原则的实现

其改进的地方只在于聚类中心的选取，选取方法如下：

1. 随机选择一个初始聚类中心
2. 计算各个数据点到已有中心的最短距离，以此作为权值来计算下一个聚类中心【轮盘法】
3. 重复第二步，直到选出k个聚类中心为止

为什么能实现？

第二步选取下一个聚类中心的时候，当前数据点距离第一个中心的距离越大，权值就越大，这个数据点的附近就越有可能被选为第二个聚类中心。即：实现了第二个聚类中心距离第一个尽可能远！

代码实现

先看效果：

代码：

#include<iostream>
#include<vector>
#include<windows.h>
#include<time.h>
using namespace std;
#define random(x) (rand()%x)
#define oo 9999999
vector<double> v;
vector<double> v1, center;
vector<vector<double> > cluster;
double abs(double a){
    if(a >=0)
        return a;
    return (-1)*a;
}
void printV(vector<double> c){
    for(int i = 0; i < c.size(); i++)
        cout<<c[i]<<',';
    cout<<endl;
}
void kmeansPlus(int k){
    int i, n = v.size();
    double c = v[random(n)];
    cout<<"第1个聚类中心："<<c<<endl;
    center.push_back(c);
    while(center.size() < k){//找出k个聚类中心为止
        double sum = 0;
        for(int j = 0; j < v.size(); j++){
            double minDis = oo;
            for(i = 0; i < center.size(); i++){
                minDis = min(minDis, abs(v[j] - center[i]));
            }
            if(j)//制作轮盘
                v1.push_back(v1[j-1] + minDis);
            else
                v1.push_back(minDis);
            sum += minDis;
        }
        Sleep(1);
        srand((unsigned)clock());
        double p = random(100)/100.0*v1[n-1];//轮盘指针
        for(i = 0; i < v1.size() && v1[i] < p; i++);
        i--;
        printf("第%d个聚类中心：%.2f\n",center.size()+1,v[i]);
        center.push_back(v[i]);//下一个聚类中心
        v1.clear();
    }
    //聚类
    cluster.resize(k);
    for(i = 0; i < n; i++){
        double minDis = oo;
        int clu;
        for(int j = 0; j < k; j++){
            if(minDis > abs(center[j]-v[i])){
                minDis = abs(center[j]-v[i]);
                clu = j;
            }
        }
        cluster[clu].push_back(v[i]);
    }
}
int main()
{
    for(int i = 0; i < 100; i++){
        srand((unsigned)clock());
        Sleep(1);
        if(i % 10 == 0)//模拟偏差数据
            v.push_back(10 + (random(200) - 99) / 5.0);
        else//模拟真实数据
            v.push_back(10 + (random(20) - 10) / 20.0);
    }
    int i = 0, k = 3;
        kmeansPlus(k);
        for(int i = 0; i < k; i++){
            printf("第%d类\n", i+1);
            printV(cluster[i]);
        }

	return 0;
}

均值聚类算法的两个讨论

1. 我们希望将数据划分为k类，那这个k怎么确定？

   一般根据题目判断，分为几类会比较好描述，就分几类。

   比如“哪几个城市的消费习惯比较接近”这个问题，取k=2或3都比较合适。k=2时描述可以是：第一类城市消费水平较高，第二类消费水平较低。k=3时则将各个城市的消费水平分为高、中、低三档。

2. 数据量纲不一致怎么办？

   比如我们遇到了一组物什的性质描述数据，其中一个数据量纲是长度（m）一个为重量（t），二者差异太大/直接计算的数据没有意义怎么办？

   使用公式$\frac{X_i-X_{平均}}{X_{标准差}}$对数据进行标准化。再使用标准化以后的数据来聚类即可。