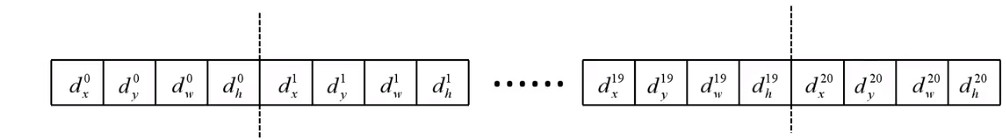计算机视觉算法——目标检测网络总结

由于后面工作方向的需要，也是自己的兴趣，我决定补习下计算机视觉算法相关的知识点，参考的学习资料主要是B站Up主霹雳吧啦Wz，强推一下，Up主的分享非常的细致认真，从他这里入门是个不错的选择，Up主也有自己的CSDN博客，我这里主要是作为课程的笔记，也会加入一些自己的理解，我也只是个入门的小白，如果有错误还请读者指正。

目标检测网络是计算机视觉一个重要的应用领域，主要分为One-Stage和Two-Stage两类方法，下面开始逐个总结各个图像分类网络的特点。

1. RCNN系列

RCNN系列是由RCNN->Fast RCNN->Faster RCNN组成，三个网络的框架分别如下图所示：
RCNN网络框架：

Fast RCNN网络框架：

Faster RCNN网络框架：

下面分别介绍这三个网络细节

1.1 RCNN

RCNN是2014年提出的，一经提出就将目标检测准确率提升了30%

1.1.1 关键知识点——网络结构及特点

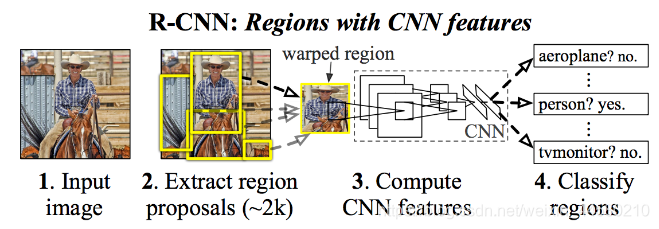
RCNN网络结构如下图所示：
该算法主要分为四个步骤：

1. 使用Selective Search方法在图像上生成1000至2000个候选区域；
   Selective Search算法是通过图像分割的方法得到一些原始区域，然后使用合并策略将区域合并从而得到一个层次化的区域结构，而这些结构中就包含着可能需要检测的物体。
2. 对每个候选区域使用深度网络（图像分类网络）提取特征；
   将2000个候选区域缩放到$227\times 227$个像素大小，然后将候选区域输入实现训练好的AlexNet CNN网络获得4096维的特征，即$2000\times 4096$维的矩阵。
3. 将特征送入每一类的SVM分类器，判断该区域是否属于该类；
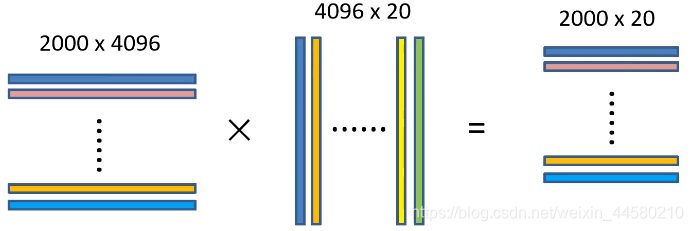
   将$2000\times 4096$维特征与20个SVM分类器组成的$4096\times 20$维权重矩阵相乘，获得$2000\times 20$维矩阵，该矩阵表示每个建议框是某个目标分类的得分，如下图所示：
   分别对上述$2000\times 20$维矩阵中每一列即每一列进行非极大值抑制剔除重叠建议框，得到该类中得分最好的建议框。非极大值抑制算法在后文介绍。
4. 使用回归器精细修正候选框位置；
   对通过非极大值抑制处理后的剩余边界框进行进一步筛选，接着分别用20个回归器对上述20个类别的建议框进行回归操作，最终得到每个类别修正后得分最高的边界框，这个回归操作在后面的Fast RCNN进行详解。

1.1.2 关键知识点——RCNN存在的问题

1. 测试速度慢，测试一张图片在CPU上需要53S，使用Selective Search算法提取候选框需要2S，一张图像内候选框之间存在大量重叠，提取特征操作存在大量冗余；
2. 训练速度慢，过程极其繁琐，不仅需要训练图像分类网络，还需要训练SVM分类器、Bounding Box回归器，训练过程都是相互独立的；
3. 训练所需空间大，对于SVM和Bounding Box回归训练，需要从每个图像中的每个目标候选框提取特征，并写入磁盘，对于非常深的网络，训练集上5K图像上提取的特征需要数百GB的存储空间。

1.1.3 关键知识点——非极大值抑制算法（NMS）

RCNN中应用的非极大值抑制算法的步骤如下：

1. 在当前类别的候选边界框中寻找得分最高的边界框；
2. 计算其他边界框与该边界框的IOU值；
3. 删除所有IOU值大于给定阈值的目边界框；
   经过上述步骤后就将最高得分的目标保存下来，再在剩下的边界框中寻找得分最高的边界框重复上述步骤。其中IOU值的计算即两个边界框交集的区域面积除以两个边界框并集区域面积，越大说明两个边界框重合区域越大，两个边界框越有可能检测到同一物体。

1.2 Fast RCNN

Fast RCNN使用VGG16作为网络的Backbone，与RCNN相比训练时间快了9倍，推理测试时间快了213倍，准确率从62%提高到66%

1.2.1 关键知识点——网络结构及特点

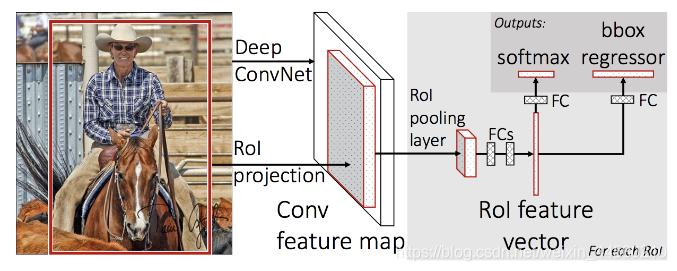
Fast RCNN网络结构如下图所示：

该算法主要有如下几个步骤：

1. 使用Selective Search方法在图像上生成1000至2000个候选区域
   该步骤与RCNN相同，在此不进行赘述。
2. 将图像输入网络得到相应的特征图，将Selective Search生成的候选框投影到特征图上得到相应的特征矩阵
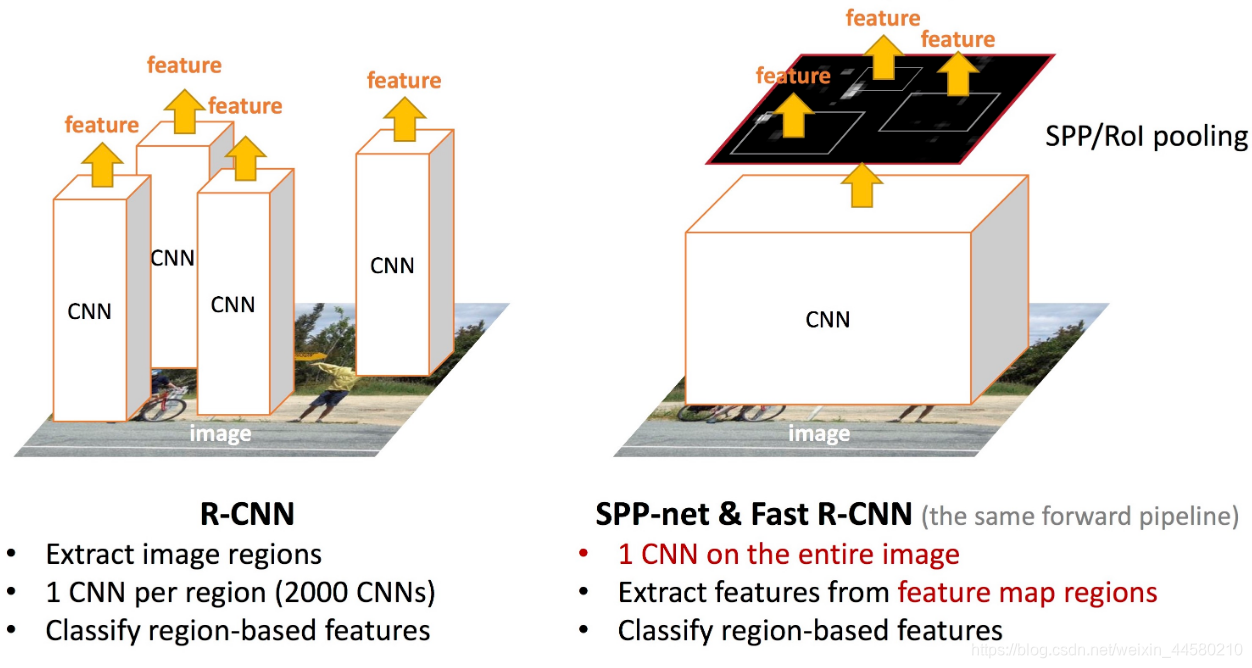
   在RCNN中是将第一步获得的2000个候选区域缩放到同一大小后如数到特征提取网络中，而FastRCNN是将整张图像送入网络，紧接着从特征图上提取相应的候选区域，这样做的好处是避免了候选区域的特征重复计算。下面这张图就说明了RCNN和FastRCNN在这一关键步骤的不同之处
   
3. 将每个特征矩阵通过ROI Pooling层缩放到$7\times 7$大小的特征图，接着将特征图展平通过一系列全连接成得到预测结果
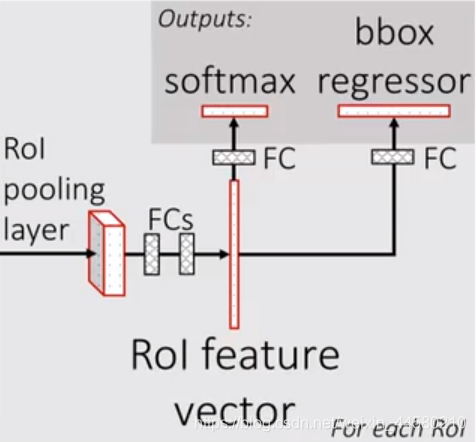
   所谓ROI pooling就是将输出特征划分为$7\times 7$的网格，每个网络输出该网格数值最大的特征值，最后无论原特征矩阵多大最终都得到一个$7\times 7$大小的特征图，接下来我们看一下最后全连接层的结构，如下图所示：
   
   将$7\times 7$大小的特征图进行展平处理后通过两个全连接层后得到ROI feature vector，接下来并联了两个全连接层，最后就进行损失计算。

1.2.1 关键知识点——目标检测多任务损失

前文提到ROI Feature Vector后面并联了两个全连接层，其中左侧全连接层对接分类器，右侧全连接层对接边界框回归器，两个不同功能的模块组成目标检测中的多任务损失，在目标检测网络中这是通用的一种损失构建方式，下面具体介绍：

1. 分类器：分类器输出$N+1$个类别的概率（其中$N$为检测目标的种类，1为背景的概率），因此其对应的全连接层共$N+1$个节点，其中$N$个种类概率是通过softmax输出的，因此这$N$个种类的概率和为1，因此
   
2. 边界框回归器：边界框回归器输出对应$N+1$个类别的候选边界框回归参数$d_x,d_y,d_w,d_h$，因此其对应的全连接层共$(N+1)\times 4$个节点
   
   候选框相关的计算公式如下：$${\hat{G}}_x=P_w{d}_x(P)+P_x$$$${\hat{G}}_y=P_h{d}_y(P)+P_y$$$${\hat{G}}_w=P_w\exp \left(d_w(P)\right)$$$${\hat{G}}_h=P_h\exp \left(d_h(P)\right)$$其中$P_x,P_y,P_w,P_h$分别为候选框的中心$x,y$坐标以及宽高，${\hat{G}}_x,{\hat{G}}_y,{\hat{G}}_w,{\hat{G}}_h$分别为最终预测的边界框中心$x,y$坐标以及宽高，那么$d_x,d_y,d_w,d_h$就分别是对候选框的中心和宽高调整的参数。
3. 基于以上分类器和回归器计算的多任务损失如下：$$L\left(p,u,t^u,v\right)=L_{cls}(p,u)+\lambda [u\ge 1]L_{loc}\left(t^u,v\right)$$其中$p$是分类器预测的softmax概率分布$p=\left(p_0,\dots ,p_k\right)$，$u$对应目标真实分类标签，$t^u$对应边界框回归器预测的对应类别$\left(t_x^u,t_y^u,t_w^u,t_h^u\right)$，$v$对应真实目标的边界框回归参数$\left(v_x,v_y,v_w,v_h\right)$。
   分类损失函数计算公式为：$$L_{cls}(p,u)=-\log p_u$$这里的$p_u$指的就是当前分类器预测结果为类别$u$的概率，我们知道，于多分类问题，我们通常采用交叉熵损失（Cross Entropy Loss），计算公式如下：$$H=-\sum _i{p}_i^{\ast }\log \left(p_i\right)$$其中$p_i^{\ast }$为one-hot编码的真实标签值，也就是说，该标签值只有在正确标签值的位置才为1，其他位置都为0，因此$L_{cls}(p,u)$实际就是交叉熵损失
   边界框回归损失计算公式为： L l o c ( t u , v ) = ∑ i ∈ { x , y , w , h } smooth ⁡ L 1 ( t i u − v i ) L_{l o c}\left(t^{u}, v\right)=\sum_{i \in\{x, y, w, h\}} \operatorname{smooth}_{L_{1}}\left(t_{i}^{u}-v_{i}\right) Lloc​(tu,v)=i∈{x,y,w,h}∑​smoothL1​​(tiu​−vi​)$${\mathrm{smooth}}_{L_1}(x)=\{\begin{array}{ll}0.5x^2& \text{ if }|x|<1\\ |x|-0.5& \text{ otherwise }\end{array}$$此外$\lambda$为两类损失的权重系数，$[u\le 1]$是艾弗森括号，sunshi它的作用是控制确实有目标物体存在的正样本才会计算边界框回归损失。

1.2.3 关键知识点——训练数据的采样

数据平衡在网路训练中是非常重要的：

1. 在FastRCNN的训练中，采用的mini-batches的大小为128，但是使用的训练数据并不是这128张图通过Selective Search算法中获得的2000个候选框，而是从每张图里面采样64个候选框，其中25%的候选框为与GroundTruth的IOU大于0.5，我们可以将这些候选框视为正样本，剩下的候选框与GroundTruth的IOU为0.1到0.5，这些候选框可以视为负样本
2. 通过这样的数据采样手段可以保证我们每次采样过程中获得的正负样本基本都是均衡的，这样对于最后的训练结果的提升是有非常有帮助的。

1.3 Faster-RCNN

Faster R-CNN同样使用的是VGG16作为网络的Backbone,推理速度在GPU上达到了5fps，达到了接近实时的水平

1.3.1 关键知识点——网络结构及特点

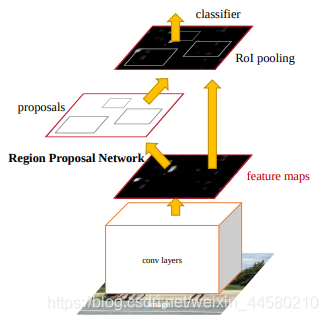
Faster-RCNN网络结构如下：

Faster-RCNN已经是一个端到端的网络了，该算法主要有如下几个步骤：

1. 将图像输入网络得到相应的特征图
   该步骤与Fast RCNN相同，在此就不再进行赘述。
2. 使用RPN结构生成候选框，将RPN生成的候选框投影到特征图上后获得相应的特征矩阵
   这一步就是Faster RCNN的精华，前文我们提到，基于传统分割方法的Selective Search算法提取候选框需要2S，这相对网络的其他推理部分是非常耗时的，作者因此将这一部分也替换成网络结构，实现了端到端的网路推理，具体的RPN网络结构设计细节参考下文关键知识点。
3. 将每个特征矩阵通过ROI Poling层缩放到$7\times 7$大小的特征图，接着将特征图展平通过一系列全连接层得到预测结果；
   该步骤与Fast RCNN相同，在此不再进行赘述。

1.3.2 关键知识点——RPN网络

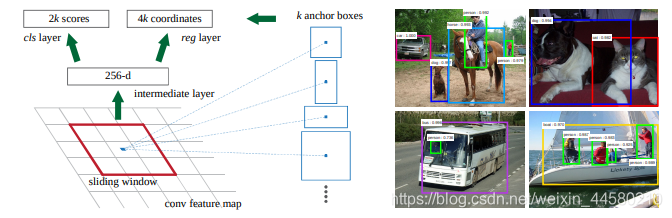
RPN网络结构如下图所示：

1. 网络结构细节如下，RPN网络同Fast RCNN网络是通用的VGG16作为特征提取的backbone，因此上图拿到的实际上就是VGG16提取的特征图，对于特征图上的每个$3\times 3$的滑动窗口，计算出特征图中滑动窗口中心位置对应原始图像上的中心点坐标以及基于原始图像上的中心点坐标生成$k$个Anchor Boxes，根据滑动窗口里的256维向量（ZF网络作为Backbone为256维，而VGG网络为512维），对于每个Anchor Box计算出2个概率（前景、背景的概率，这里不进行分类）以及4个坐标，也就是说，也就是说每个滑动窗口会输出$2k$个概率以及$4k$个坐标。在论文中提到的Anchor Box一共有3种尺度（$128^2,256^2,512^2$）和3种比例（$1:1,1:2,2:1$），也就是说这里的$k=9$，如下图所示：
   这里值得注意的一点是VGG的感受野是$228$，而anchor的尺度最大的会达到$512\times 512$，这相当于是用一个小的感受野去预测一个大的物体，在论文中作者有提到这一点，并认为这是可行的。
2. 多任务损失计算细节如下，RPN网络的的多任务损失定义如下：
   L ( { p i } , { t i } ) = 1 N c l s ∑ i L c l s ( p i , p i ∗ ) + λ 1 N r e g ∑ i p i ∗ L reg  ( t i , t i ∗ ) L\left(\left\{p_{i}\right\},\left\{t_{i}\right\}\right)=\frac{1}{N_{c l s}} \sum_{i} L_{c l s}\left(p_{i}, p_{i}^{*}\right)+\lambda \frac{1}{N_{reg}} \sum_{i} p_{i}^{*} L_{\text {reg }}\left(t_{i}, t_{i}^{*}\right) L({pi​},{ti​})=Ncls​1​i∑​Lcls​(pi​,pi∗​)+λNreg​1​i∑​pi∗​Lreg ​(ti​,ti∗​)其中：
   $p_i$表示第i个Anchor预测为真实标签的概率；
   $p_i^{\ast }$为正样本时为1，为负样本时为0，这和Faster RCNN中的艾弗森括号的作用是相同的；
   $t_i$表示预测第$i$个Anchor的边界框回归参数；
   $t_i^{\ast }$表示第$i$个Anchor对应的Ground Truth Box；
   $N_{cls}$表示一个mini-batch中的所有样本数量；
   $N_{reg}$表示Anchor位置的个数（注意不是Anchor的个数，Anchor的个数等于Anchor的位置个数乘以$k$）；
   上述损失计算公式中前一部分为分类损失，如果使用多类别的Softmax交叉熵损失，因为此处的类别只有前景和背景两类，如下，那么对于每个Anchor分别计算出属于前景和背景的概率，对于$k$个Anchor就需要计算出$2k$个值：
   
   具体公式如下所示：$$L_{cls}=-\log (p_i)$$如果使用的是二分类的交叉熵损失，那么此处对于每个Anchor就只计算出一个概率，如下，对于$k$个Anchor就需要计算出$k$个值：
   
   具体公式如下所示：$$L_{cls}=-\left[p_i^{\ast }\log \left(p_i\right)+\left(1-p_i^{\ast }\right)\log \left(1-p_i\right)\right]$$损失计算公式中的后一部分为边界框回归损失，边界框回归损失的形式和Faster RCNN的形式是一样的，使用的也是Smooth L1损失，在这里就不进行赘述了。

1.3.3 关键知识点——RPN Loss和Fast RCNN Loss联合训练

原论文中采用RPN Loss和Fast RCNN Loss联合训练的方法如下：

1. 利用ImageNet预训练分类模型初始化前置卷积网络层参数，并开始单独训练RPN网络参数；
2. 固定RPN网络独有的卷积以及全连接层参数，利用ImageNet预训练分类模型初始化前置卷积网络参数，并利用RPN网络生成的目标建议框去训练Fast RCNN网络参数；
3. 固定利用Fast RCNN训练好的前置卷积网络层参数，去微调RPN网络独有的卷积层以及全连接层参数；
4. 同样保持固定前置卷积网络层参数，去微调Fast RCNN网络的全连接层参数。最后PRN网路与Fast RCNN网络共享前置网络层参数，构成一个统一网络。

2. SSD系列

SSD是2016年在ECCV上发表的论文，在$300\times 300$的网络上达到了74.3%mAP以及59FPS，在$512\times 512$的网络上，以76.3%mAP超越了Faster RCNN的73.2%mAP

2.1 SSD

2.1.1 关键知识点——网络结构及特点

在前文提到的Faster RCNN中存在两个问题分别是对

1. 小目标检测效果较差：Faster RCNN中采用的都是高层特征信息，这部分信息细节信息保留少，因此对于小目标检测效果差；
2. 模型大、检测速度慢：Faster RCNN采用的是Two Stage的结构，这是导致检测速度慢的主要原因。

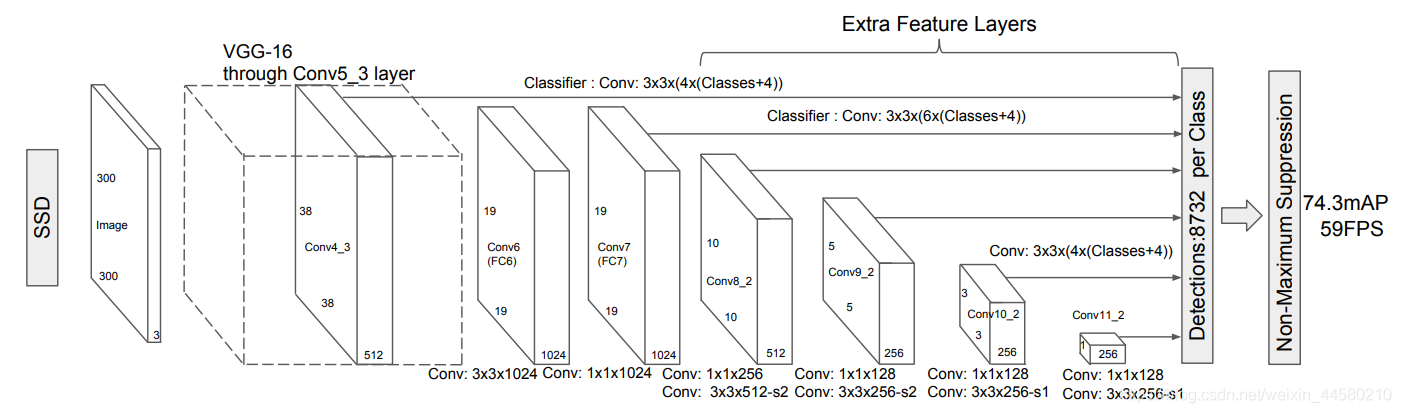
而SSD网络结构如下：

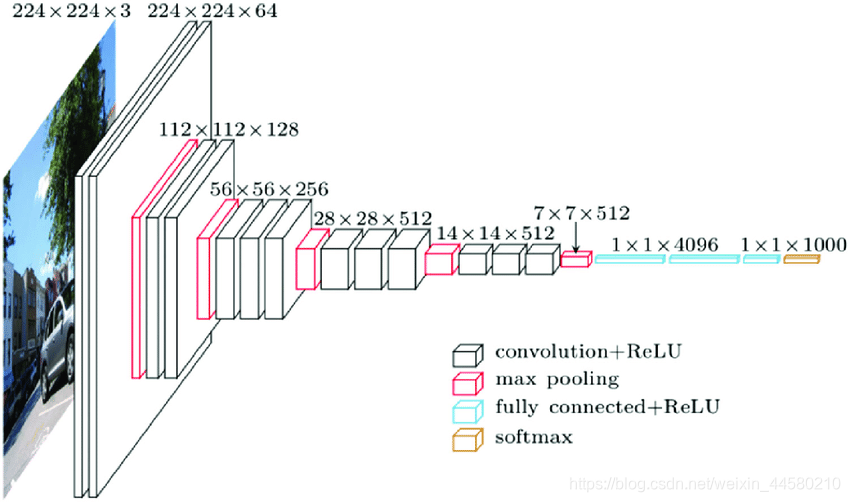
从上图中可以看到，SSD的网络结构为One-Stage结构，并且在不同特征尺度上预测不同尺度的目标，下面我们具体来说，SSD网络是使用VGG16作为backbone，如下图所示：

1. . SSD网络中的Conv4_3就对应VGG网络中$28\times 28\times 512$卷积模块的第三个卷积层，输出为$38\times 38\times 512$的特征矩阵；
2. SSD网络中的Conv5_3就对应VGG网络中$14\times 14\times 512$卷积模块的第三个卷积层位置，输出为$19\times 19\times 1024$的特征矩阵；
3. SSD网络中的Conv6就对应VGG网络中的第一个全连接层，由于SSD网络对VGG网络中的$7\times 7\times 512$的池化层进行了修改，因此输出仍然为$19\times 19\times 1024$的特征矩阵；
4. SSD网络中的Conv7就对应VGG网络中的第二个全连接层，输出为$19\times 19\times 512$的特征矩阵；
5. 紧接着SSD网络中还跟着四个卷积层，输出分别是$10\times 10\times 512$，$5\times 5\times 256$，$3\times 3\times 256$，$1\times 1\times 256$的特征矩阵，特征矩阵的尺寸越来越小，说明所提取的特征也越来越高级，我们会用大尺寸的特征矩阵预测较小的目标，用小尺寸的特征矩阵预测较大的目标，因此以上提到的所有输出特征矩阵都会输出到Prediction层进行预测。

2.2.1 关键知识点——Default Box的设定

SSD中Default Box和前文Faster RCNN中提到的RPN网络的中Anchor Box是同一个概念，但是RPN网络的特征层就一层，而SSD网络用于预测的特征层是多层，因此Defaul Box的设定会更为复杂，具体规则如下：

1. 对与SSD中每一个预测特征层的Default Box都会有不同的尺度(Scale)和长宽比(Aspect)，论文中规定，对于Aspect，不同的特征层都只有 { 1 , 2 , 3 , 1 / 2 , 1 / 3 } \left\{1,2,3, {1}/{2}, {1}/{3}\right\} {1,2,3,1/2,1/3}这五种类型，而对于Scale，不同特征层则不相同，第$k$个预测特征层的Default Box的Scale的公式如下:$$s_k=s_{\min }+\frac{s_{\max }-s_{\min }}{m-1}(k-1),k\in [1,m]$$其中，$s_{min}$为最小的尺度,$s_{max}$为最大的尺度。最后还有一个规则是，对于Aspect为1的Default Box，还有一个额外的$\sqrt{s_k{s}_{k+1}}$的尺寸，因此综上所属对于每一个特征层一共有6中不同的Default Box。
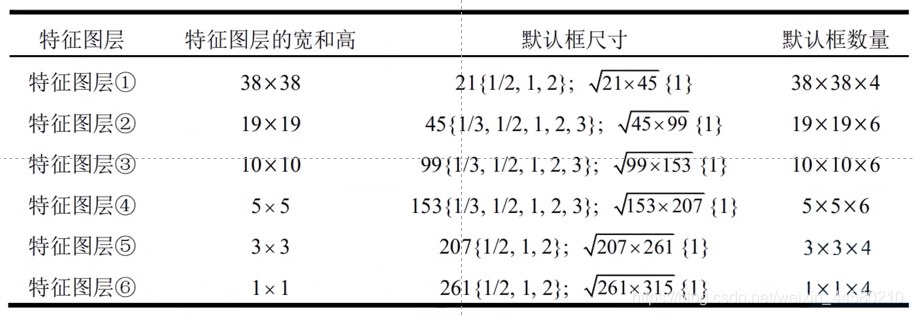
2. 在学习视频中作者总结了如下一张表格,说明了SSD中具体的Default Box的设置
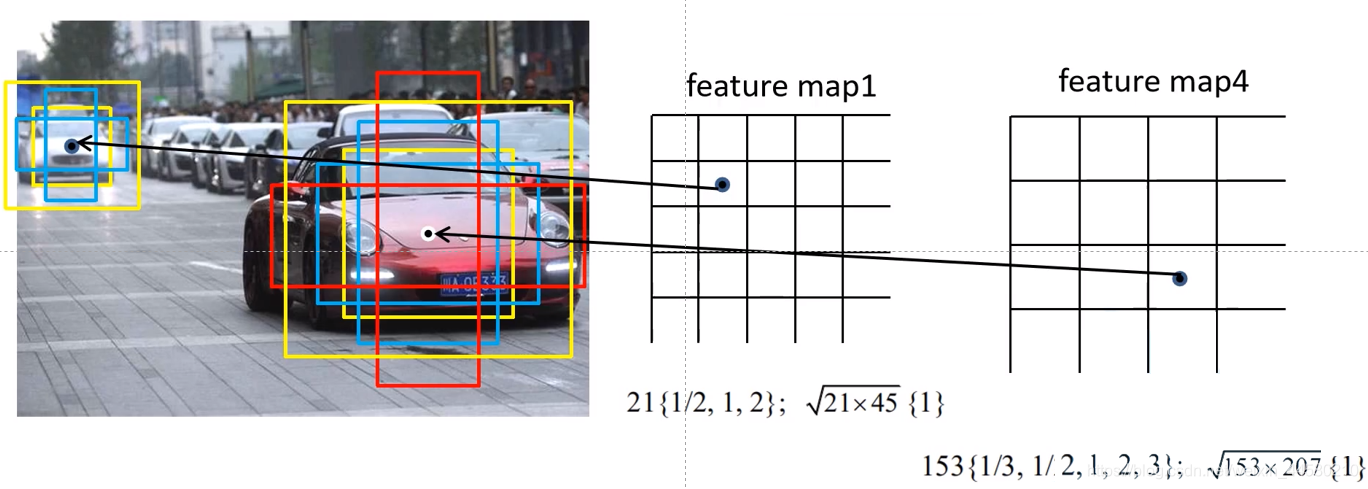
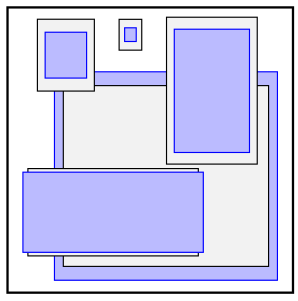
   细心的同学可能会注意到，在第一、五、六个特征层中，实际Default Box的尺寸只有4种，那是因为在这几层忽略了Aspect为3和1/3的两个Default Box，那么整个SSD网络中Default Box的数量一共为$$38\times 38\times 4+19\times 19\times 6+10\times 10\times 6+5\times 5\times 6+3\times 3\times 4+1\times 1\times 4=8732$$我们这里还需要注意的一点是，这里的尺度Scale指的是原图中Default Box大小，对于这一点视频作者还画了一个图我觉得非常有助于我们理解，如下
   对于第一个特征层，左上角的Anchor使用如图三种Scale较小的Default Box（大小为21个像素左右）去检测左上角的那辆面积较小的白车，而对于第四个特征层，中间区域的Anchor使用如果所示的六种Scale较大的Default Box（大小为153个像素左右）去检测中间那辆面积较大的红车。

2.2.2 关键知识点——Predictor的实现

这里所谓的Predictor其实指的就是最后的用于进行分类和回归损失计算，在Faster RCNN中最后获得的特征矩阵是通过ROI Pooling Layer变换成大小相同的特征矩阵，再展开成ROI Pooling Vector，最后通过两个全连接层再进行分类和回归损失计算的，而在SSD中，是通过小尺寸的卷积核对特征矩阵进行变换在进行分类和回归层计算的，具体说来

1. 对于尺寸为$m\times n\times p$的特征矩阵，是通过$3\times 3\times p$的卷积核来生成概率分数以及相对Default Box的坐标偏移量，那么一共需要多少个这样的卷积核呢？对于每个Anchor会输出$k$个Default Box，而每个Default Box会输出$c$个类别的概率分数（包括背景的概率）以及$4$个坐标偏移量，因此对于每个Anchor会需要$(c+4)k$个卷积和，对于一个$m\times n$的特征矩阵就会需要$(c+4)kmn$个卷积核。
2. 这里有一个值得注意的是，在SSD中每个Default Box输出$(c+4)$个值，而在Faster RCNN中是对于每个类别都输出一个位置偏移量的估计，因此是$c\times 4$个值，因此Faster RCNN中输入到Predictor中的值要多一些。
3. 当获得网路输出的概率分数以及坐标偏移量后，接下来就是进行损失计算了，损失计算公式如下：$$L(x,c,l,g)=\frac{1}{N}\left(L_{\text{conf }}(x,c{)}_i+{\alpha }^{\prime }{L}_{loc}(x,l,g)\right)$$其中$N$为匹配到正样本的个数，损失计算公式中前半部分为类别损失，后半部分为定位损失：
   对于类别损失，具体计算公式为$$L_{\text{conf }}(x,c)=-\sum _{i\in \text{ Pos }}^N{x}_{ij}^p\log \left({\hat{c}}_i^p\right)-\sum _{i\in Neg}\log \left({\hat{c}}_i^0\right)\text{ where }{\hat{c}}_i^p=\frac{\exp \left(c_i^p\right)}{{\sum }_p\exp \left(c_i^p\right)}$$从类别损失的计算公式可以看出来，类别损失又可以分为两部分，前半部分为正样本类别损失的计算公式，所谓正样本就是与Ground Truth Box的IOU大于0.5的Default Box。第二部分为负样本类别损失的计算公式，所谓负样本就是与Ground Truth Box的IOU为0.1到0.5的Default Box，这些正负样本的损失其实就是Softmax交叉熵损失，其中：
   ${\hat{c}}_i^p$为预测第$i$个Default Box对应的Ground Truth类别为$P$的类别概率，通过公式可以看出其实就是一个经过Softmax处理后的一个概率；
   x i j p = { 0 , 1 } x_{i j}^{p}=\{0,1\} xijp​={0,1}表示第$i$个Default Box匹配到的第$j$个Ground Truth Box，而第$j$个Ground Truth Box的类别又为$P$时该值为1，否则为0，我理解为类似于艾弗森括号的作用；
   ${\hat{c}}_i^p$为预测第$i$个Default Box对应的Ground Truth类别为背景的概率；
   对于定位损失，仅仅是针对正样本而言，和Faster RCNN的定位损失函数是一样的，具体公式如下： L l o c ( x , l , g ) = ∑ i ∈ Pos ⁡ N ∑ m ∈ { c x , c y , w , h } x i j k smooth ⁡ L 1 ( l i m − g ^ j m ) L_{l o c}(x, l, g)=\sum_{i \in \operatorname{Pos}}^{N} \sum_{m \in\{c x, c y, w, h\}} x_{i j}^{k} \operatorname{smooth}_{\mathrm{L} 1}\left(l_{i}^{m}-\hat{g}_{j}^{m}\right) Lloc​(x,l,g)=i∈Pos∑N​m∈{cx,cy,w,h}∑​xijk​smoothL1​(lim​−g^​jm​)其中$${\hat{g}}_j^{cx}=\left(g_j^{cx}-d_i^{cx}\right)/d_i^w$$$${\hat{g}}_j^{cy}=\left(g_j^{cy}-d_i^{cy}\right)/d_i^h$$$${\hat{g}}_j^w=\log \left(\frac{g_j^w}{d_i^w}\right)$$$${\hat{g}}_j^h=\log \left(\frac{g_j^h}{d_i^h}\right)$$$l_i^m$为预测对应第$i$个正样本回归参数，${\hat{g}}_j^m$为正样本$i$匹配的第$j$个Ground Truth Box的回归参数，$g_j^m$为第$j$个Ground Truth Box的位置和长宽参数，Smooth L1的计算公式为：$${\mathrm{smooth}}_{L_1}(x)=\{\begin{array}{ll}0.5x^2& \text{ if }|x|<1\\ |x|-0.5& \text{ otherwise }\end{array}$$

3. YOLO系列

YOLO是我之前接触过的一个算法，当时还写过一篇博客关于如何调用Darknet版的YOLO v3的博客深度学习框架YOLOv3的C++调用，但是当时只是觉得好用却不懂原理，这里总结下。

3.1 YOLO v1

YOLO v1是和SSD同年在CVPR上发表的文章，当时的速度达到了45FPS，准确率达到了63.4mAP，速度和准确率都不及SSD，但是经过一步一步的发展， YOLO系列最终在性能上超过了SSD，这里先介绍下YOLO v1的基本方法

3.1.1 关键知识点——网络结构及特点

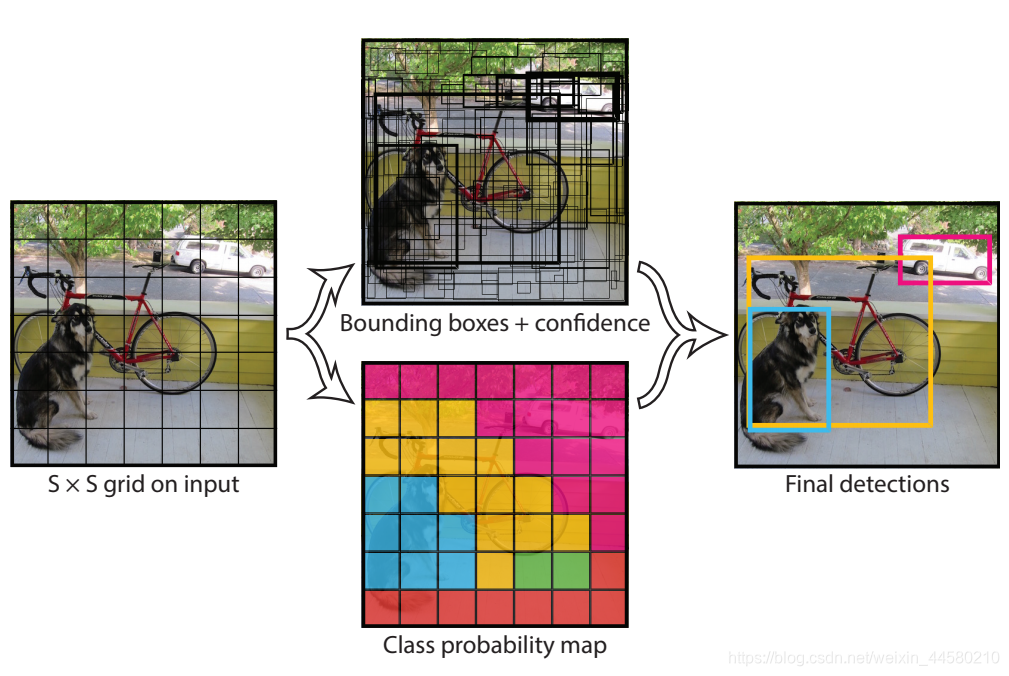
YOLO v1中实现目标检测的的主要思想如下：

1. 将一幅图像分成$S\times S$个网格，如果某个物体的中心落在这个网格中，则这个网格就负责预测这个物体；
2. 每个网格要预测$B$个Bounding Box（在YOLO v1中没有Faster RCNN和SSD中的Anchor的概念），每个Bounding Box包括4个位置参数和1个Confidence值，除此之外，每个网格还要预测$C$个类别的分数。即每个网格输出的参数个数为$B\times (4+1)+C$，其中，位置参数包括$x,y,w,h$这4个参数，$x,y$表示预测的Bounding Box的中心相对对应网格中心的偏移，而$w,h$表示Bounding Box的长宽相对整幅图像长宽的比，Confidence这个参数在Faster RCNN和SSD中都是没有的，具体来说，Confidence的计算公式为：$$\mathrm{Pr}(\text{ Object })\ast {\text{ IOU }}_{\text{pred }}^{\text{truth }}$$其中，$\mathrm{Pr}(\text{ Object })$指的是当Bounding Box中存在物体时，该值为1，不存在物体时，该值为0，${\text{ IOU }}_{\text{pred }}^{\text{truth }}$指的是预测的Bounding Box与真实Bounding Box的交并比。在Test时，网格除了会输出每一个目标的Bounding Box的位置之外，还会输出每一个目标的检测概率，这个概率的计算公式为：$$\mathrm{Pr}\left({\text{ Class }}_i\mid \text{ Object }\right)\ast \mathrm{Pr}(\text{ Object })\ast {\text{ IOU }}_{\text{pred }}^{\text{truth }}=\mathrm{Pr}\left({\text{ Class }}_i\right)\ast {\text{ IOU }}_{\text{pred }}^{\text{truth }}$$其中$\mathrm{Pr}\left({\text{ Class }}_i\mid \text{ Object }\right)$为网格预测的$C$个类别的分数，而$\mathrm{Pr}(\text{ Object })\ast {\text{ IOU }}_{\text{pred }}^{\text{truth }}$就是预测的Bounding Box的Confidence值，从化简公式可以看出，目标的检测概率既包含了该目标为某一个类别的概率，也包含了该目标与真实边界框的交并比。（因为是在Test时使用，这个目标的检测概率只是一个评测指标吗？这个需要后面自己去验证下）

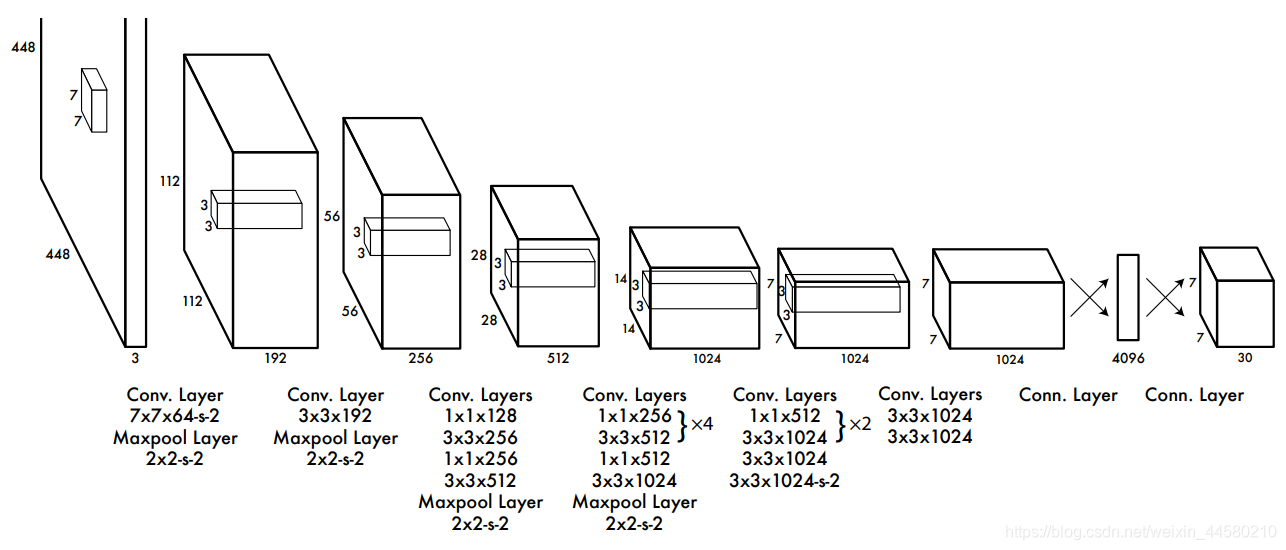
YOLO v1网络的具体结构如下：

1. 使用多层的卷积作为BackBone进行特征提取，最终输出$7\times 7\times 1024$的特征矩阵；
2. 将$7\times 7\times 1024$的特征矩阵展平为向量，再连接一个全连接网络，输出长度为$4096$维的特征向量；
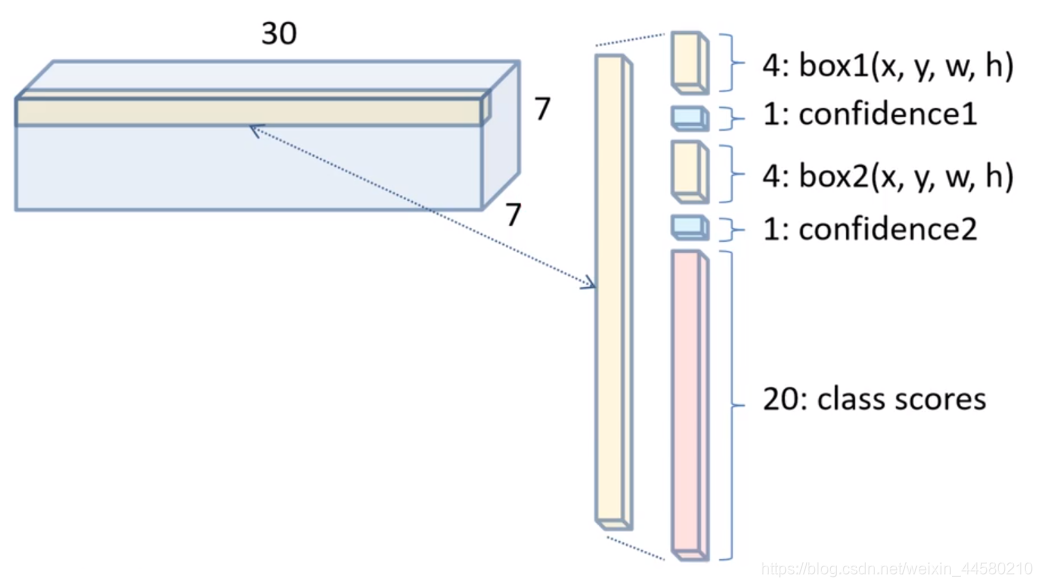
3. 将$4096$维的特征向量再接一个全连接网络，输出长度为$1470$维的特征向量，并最终将向量Reshape为$7\times 7\times 30$的特征矩阵作为输出。那么输出特征矩阵的尺寸为什么为$7\times 7\times 30$呢？结合前文所说的YOLO v1进行目标检测的主要思想，我们对此进行分析，在实际的YOLO v1的搭建过程中，图像被划分为$S\times S=7\times 7$的网格，每个网格预测$B=2$个Bounding Box以及$C=20$个类别概率，即每个网格输出$B\times (4+1)+C=2\times (4+1)+20=30$个参数，因此输出的特征矩阵尺寸为$7\times 7\times 30$，如下图所示，这是可以一一对应上的。
   

3.1.2 关键知识点——损失计算函数

在YOLO v1中，采用的是误差平方和的作为损失函数计算公式，具体公式如下：
如上图所示，损失计算函数主要包括三部分，下sunshi面分别介绍

1. Bounding Box损失：对于Bounding Box的损失计算主要是对$(x,y,w,h)$四个预测参数相对真实值的误差进行平方求和，其中表示位置的$x,y$是直接计算，而表示宽高的$w,h$是先开根号再计算，开根号的目的是为了保证大目标和小目标在偏移相同距离时，小目标的损失值要更大一些。
2. Confidence损失：Confidence分为两部分，其中${\sum }_{i=0}^{S^2}{\sum }_{j=0}^B{1}_{ij}^{\text{obj }}{\left(C_i-{\hat{C}}_i\right)}^2$为正样本损失，此时真实值${\hat{C}}_i$为1，而${\lambda }_{\text{noobj }}{\sum }_{i=0}^{S^2}{\sum }_{j=0}^B{1}_{ij}^{\text{noobj }}{\left(C_i-{\hat{C}}_i\right)}^2$为负样本损失，此时真实值${\hat{C}}_i$为0。
3. Class损失：类别损失即预测与真实值的平方和损失。

3.1.3 关键知识点——YOLO v1存在的问题

1. YOLO v1对群体性的小目标检测效果差，造成这个问题的主要原因是对每个网格只预测一种类型的目标以及两个Bounding Box，因此对于小目标的检测能力有限；
2. 对于具备新比例的目标检测效果差；
3. 网络主要的检测误差来源与定位不准确，造成这个问题的主要原因YOLO v1中是直接回归的目标的坐标信息，而不是像Faster RCNN和SSD那样回归到Anchor的参数；

3.2 YOLO v2

YOLO v2是发表于2017年的CVPR，由于其检测目标可以达到9000个，因此YOLO v2还有一个别名叫做YOLO 9000，从下面这张表格可以看出，YOLO v2在网络性能方面确实有了非常大的提升：
YOLO v2的论文一共分为三部分：Better、Faster、Stronger，下面主要介绍网络结构以及论文是如何各种方法提高网络性能的。

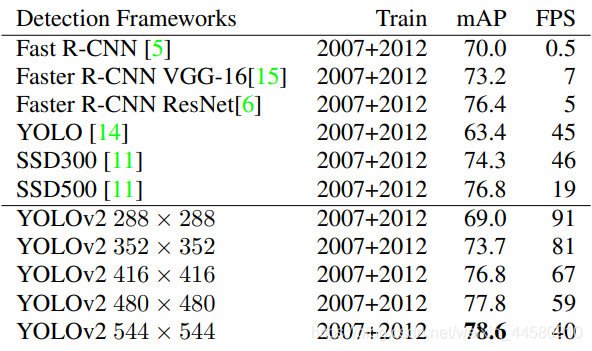
3.2.1 关键知识点——网络的结构及特点

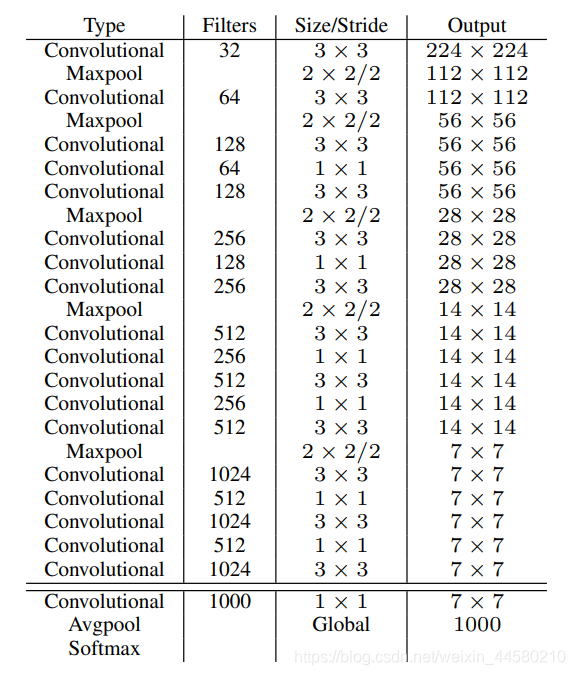
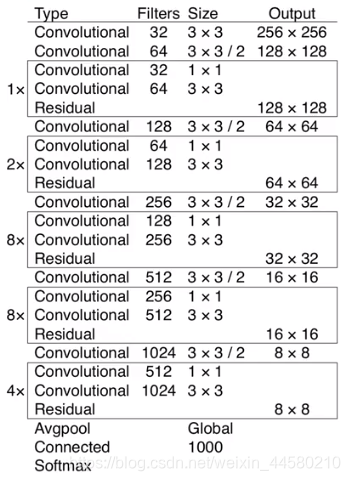
论文中用于目标检测网络的BackBone网络Darknet-19，该网络一共有19层卷积层，网络结构如下：

其中

1. 表格中每一个Convolutional层指代的都包括Conv2d-BatchNornalization-LeakyReLU这样三层结构，并且由于使用的Batch Normalization层，因此Conv2d中的卷积是没有偏置Bais的。
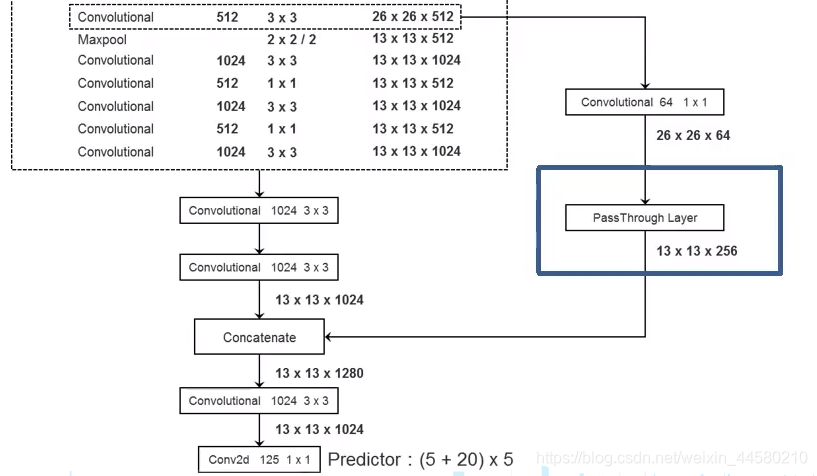
2. 在Darknet-19的基础上，如下图所示：
   
   YOLO v2再接了两个$1024\times 3\times 3$的卷积层，然后在与来自前文提到的Passthrough Layer的底层特征信息进行Concate，再接一个$1024\times 3\times 3$的卷积层，此时特征矩阵的大小为$13\times 13\times 1024$，最后再接125维的$1\times 1$矩阵，最终输出的特征矩阵的大小即为$13\times 13\times 125$。4. 我们来解释下这个输出特征矩阵维度$13\times 13\times 125$的意义，其中$13\times 13$可以理解为将图像划分为$13\times 13$的网格，每个网格输出5个Anchor Box，每个Anchor Box负责输出4个位置回归参数，1个置信度以及20个类别参数，因此每个网格一共需要输出$5\times (1+4+20)=125$个参数。

3.2.1 关键知识点——提升mAP参数的方法

论文的Better章节中一共从这一下7个方面对进行了尝试提升网络的mAP参数：

1. Batch Normalization，作者提出加入Batch Normalization层对于网络收敛有非常大的帮助，同时可以减少一系列正则化的操作（例如移除dropout层），加入Batch Normalization层后YOLO模型的mAP提升了2%。
2. High Resolution Classifier，在YOLO v1中作者使用的是$224\times 224$的图像作为训练网络的输入，而在YOLO v2网络中使用的是$448\times 448$的图像作为网络输入，采用更高分辨率的分类器可以在模型的mAP参数上提升4%。
3. Convolutional With Anchor Boxes，作者提出使用预测Bounding Box相对Anchor Box的Offset相对于直接学习Bounding Box的坐标要简化网络的学习难度，在没有使用Anchor Box时，模型的mAP为69.5，召回率为81%，而使用Anchor Box后，模型的mAP为69.2，召回率为88%，作者认为召回率的提高意味着模型有更大的提升空间。
4. Dimension Clusters，这里指的是如何获得Anchor Box的预设尺寸，在Faster RCNN以及SSD中，Anchor Box的预设尺寸更多地像是工程经验获得的，而在YOLO v2中明确提出，在训练集上使用K-Means的方式来获得Anchor Box的预设尺寸。具体说来，步骤如下：
   (1) 用来聚类的原始数据带有标注框的检测数据集，标注框的参数为 ( x j , y j , w j , h j ) , j ∈ { 1 , 2 , … , N } \left(x_{j}, y_{j}, w_{j}, h_{j}\right), j \in\{1,2, \ldots, N\} (xj​,yj​,wj​,hj​),j∈{1,2,…,N}，因为和标注框位置无关，因此这里实际用到的参数只有$w_j,h_j$；
   (2) 首先给定$k$个聚类中心点 ( W i , H i ) , i ∈ { 1 , 2 , … , k } \left(W_{i}, H_{i}\right), i \in\{1,2, \ldots, k\} (Wi​,Hi​),i∈{1,2,…,k}，其中$k$我们需要预设Anchor Box的尺寸的个数；
   (3) 计算每个标注框和聚类中心点的距离$d=1-\mathrm{IOU}$，这里计算的IOU指的是当每个标注框中心与Anchor Box中心重合的面积交并比，即 d = 1 − IOU ⁡ [ ( x j , y j , w j , h j ) , ( x j , y j , W i , H i ) ] , j ∈ { 1 , 2 , … , N } , i ∈ { 1 , 2 , … , k } d=1-\operatorname{IOU}\left[\left(x_{j}, y_{j}, w_{j}, h_{j}\right),\left(x_{j}, y_{j}, W_{i}, H_{i}\right)\right], j \in\{1,2, \ldots, N\}, i \in\{1,2, \ldots, k\} d=1−IOU[(xj​,yj​,wj​,hj​),(xj​,yj​,Wi​,Hi​)],j∈{1,2,…,N},i∈{1,2,…,k}。将每个标注框分配给距离最近的聚类中心。
   (4) 所有标注框分配完毕后，对每个簇的重新计算聚类中心$W_i^{\prime }=\frac{1}{N_i}\sum w_i,H_i^{\prime }=\frac{1}{N_i}\sum h_i$，然后重复(3)(4)步骤。
   如下图：论文中展示了在COCO数据集上VOC数据集上通过以上方法获得的不同的Achor Box的预设尺寸：
   可以观察到，白色框与紫色框在不同尺度下长宽都有些许不同。通过聚类的方式获得的相对认为人为设定的方法更加充分地利用了数据集的信息，让网络回归更加轻松。
5. Direct location prediction，在论文中，作者提出，如果直接使用Faster RCNN或者SSD中的参数回归方法，会导致在训练过程中，模型会出现不稳定的情况，而这中间导致不稳定的主要因素又是位置参数$x,y$，我们知道，Faster RCNN和SSD中的位置参数方法如下：$$x=\left(t_x\ast w_a\right)+x_a$$$$y=\left(t_y\ast h_a\right)+y_a$$其中，$t_x,t_y$为网络预测的参数，$x_a,x_b,w_a,w_b$为Anchor Box的中心坐标以及宽高，作者提出，以上公式是没有收到限制的，因此网络预测的Bounding Box位置可能出现在图像中的任何位置，因此，在YOLO v2中，作者给出的位置$$b_x=\sigma \left(t_x\right)+c_x$$$$b_y=\sigma \left(t_y\right)+c_y$$$$b_w=p_w{e}^{t_w}$$$$b_h=p_h{e}^{t_h}$$其中，$t_x,t_y,t_w,t_h$为网络预测的参数，$c_x,c_y$为该栅格左上角对应的坐标。$\sigma ()$其实就是logistic激活函数，该函数的输出可以将网络预测的输出限制在一定范围内，论文指出，通过限制网络的输出以及通过聚类的方式获得Anchor Box使得网络mAP提升了5%。
6. Fine-Grained Features，这一点指的是使用网络中更加低层的特征信息，因为低层的特征信息包含更多的细节，这对检测小目标是有帮助的，在YOLO v2中的操作方式是通过Passthrough Layer这样一种网络层将高层特征信息和底层特征信息融合的，具体说来，YOLO v2实际上就是将网络BackBone中$26\times 26\times 512$的特征取出与最后输出的$13\times 13\times 1024$的特征进行Concatenate操作，两个特征的维度不是不一样吗？对！PassThrough Layer的作用就是将$26\times 26\times 512$的特征重新组合成维度为$13\times 13\times 2048$的特征，具体操作方式如下图所示：
   通过这种方式，YOLO v2的mAP提升了1%.
7. Multi-Scale Training，即采用多尺度的训练方法，在训练过程中使用随机的输入图片大小替换掉固定的输入图片大小，具体来说，每迭代10个batch就将网络的输入图片大小进行随机选择，由于YOLO v2的网络缩放因子为32，因此输入图片的大小应该为32的整数倍，作者采用的是从 { 320 , 352 , … , 608 } \{320,352, \ldots, 608\} {320,352,…,608}这一些列大小中进行随机选择的。

3.3 YOLO v3

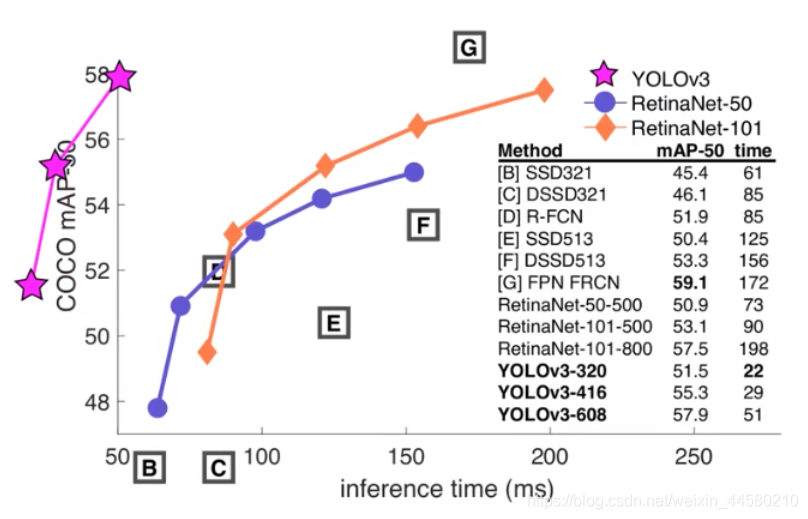
YOLO V3发表于2018年的CVPR，其优势主要体现在如下这张图中

在极高的检测速度下仍然保证了很高的mAP-50的值，下面我们来简单看下网络的特点

3.3.1 关键知识点——网络结构及特点

YOLO v3中相对YOLO v2在网络的BackBone上又有了进一步的提升，YOLO v3使用的BackBone为Darknet-53，结构如下图所示：

其特点主要如下：

1. Darknet-53和其他网络准确率以及速度的对比如下：
   
   可以看到，相对于ResNet来说，网络在运行速度上有明显优势，在准确率上也有明显优势。
2. 在Darknet-53中没有最大池化下采样层，而是通过卷基层代替了最大池化下采样层，最大池化下采样层能够增大感受野，让卷积看到更多的信息，但是它在降维的过程中丢失了一些信息，而步距等于2的卷积层相当于保留了相对更多的信息，因此效果会更好？(这是观点属于个人推测)
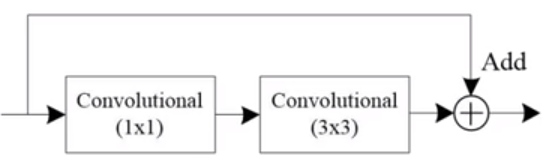
3. 上图中Convolutional模块指的是Convolution层，Batch Normalization层，Leaky ReLU层的集合，结构如下图所示：
   
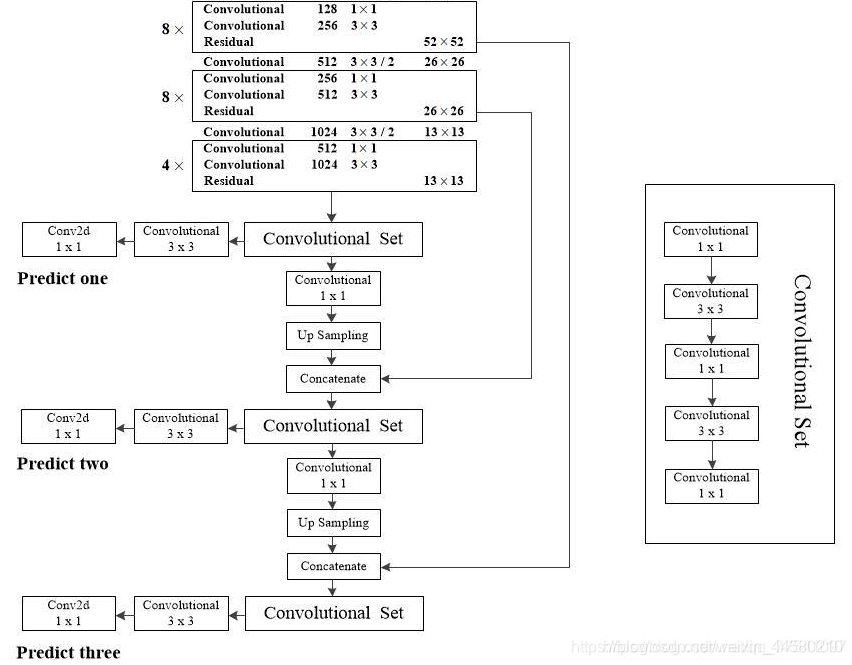
   Residual模块加上它前两层的Convolutional模块，就是我们通常理解的残差模块，结构如下图所示：
4. 在BackBone网络后接的预测特征层如下图所示，图片来源自YOLO v3网络结构分析：
   
   从BackBone网络的后三层Residual模块开始就会输出分别接到不同尺度的预测特征层，以Predict One为例，Residual输出的特征矩阵会先输入至Convolutional Set模块，Convolutional Set模块入上右图所示，是由一系列Convolutional模块组成，通过Convolutional Set模块后，
   一方面（图中向左的链路）经过Convolutional模块和$1\times 1$的卷积层输出，这里输出的特征的大小为$N\times N\times [3\ast (4+1+80)]$，其中$N$指输出特征层的维度，在Predict One中就是13，此外3指3个Anchor Box，4指位置相关的预测参数，1指Confidence，80指Coco数据集80个预测类别的分数，网路最后基于以上输出计算损失。
   另一方面（图中向右的链路）经过Convolutional模块、UpSampling模块后，和BackBone中更低层的特征进行Concate，Concate后得到的特征矩阵，通过Convolutional Set后重复以上步骤，至此就完成了网络预测特征层的搭建，这里值得注意的是相对于YOLO v2的预测特征层网络来说，YOLO v3更加充分地利用了低层网络的信息，因此YOLO v3在小物体检测的能力上有了更大的提升。

3.3.2 关键知识点——损失计算函数

在进行损失计算函数之前，我们先提一下正负样本匹配的问题，也就是我们用哪些样本来计算损失，在YOLO v3的原文中提到， 对于正样本，只将与Ground Truth的IOU最大的预测Bounding Box作为正样本计算坐标、类别和置信度损失，其他与Ground Truth的IOU大于0.5的Bouding Box直接忽略掉，而与Ground Truth的IOU小于0.5的Bounding Box作为负样本，只计置信度损失。YOLO v3的算是计算函数与前两版有较大不同，在YOLO v1中我们介绍的使用的是误差平方损失，而在YOLO v3中主要使用的是二值交叉熵损失，具体如下：

1. YOLO v3的损失函数主要由三部分组成，分别是置信度损失、类别损失、定位损失，如下所示：$$L(o,c,O,C,l,g)={\lambda }_1{L}_{\text{conf }}(o,c)+{\lambda }_2{L}_{\text{cla }}(O,C)+\lambda L_{loc}(l,g)$$其中$L_{\text{conf }}(o,c)$是置信读损失，$L_{\text{cla }}(O,C)$是分类损失，$L_{loc}(l,g)$是定位损失，${\lambda }_1,{\lambda }_2,{\lambda }_3$为各项损失的平衡系数。
2. 置信度损失采用的是二值交叉熵损失，公式如下所示：$$L_{\text{conf }}(o,c)=-\frac{{\sum }_i\left(o_i\ln \left({\hat{c}}_i\right)+\left(1-o_i\right)\ln \left(1-{\hat{c}}_i\right)\right)}{N}$$$${\hat{c}}_i=\mathrm{Sigmoid}\left(c_i\right)$$其中，$o_i\in [0,1]$表示预测目标边界框与真实目标边界框的IOU，$c$为预测值，$\hat{c}$为$c$通过Sigmoid函数得到的预测置信度，$N$为正负样本个数。
3. 类别损失采用的同样是二值交叉熵损失，公式如下：$$L_{cla}(O,C)=-\frac{{\sum }_{i\in posj\in cla}\left(O_{ij}\ln \left({\hat{C}}_{ij}\right)+\left(1-O_{ij}\right)\ln \left(1-{\hat{C}}_{ij}\right)\right)}{N_{pos}}$$$${\hat{C}}_{ij}=\mathrm{Sigmoid}\left(C_{ij}\right)$$其中 O i j ∈ { 0 , 1 } O_{i j} \in\{0,1\} Oij​∈{0,1}，表示预测目标边界框$i$中是否存在第$j$类目标，$C_{ij}$为预测值，${\hat{C}}_{ij}$为$C_{ij}$通过Sigmoid函数得到的目标概率，由于不是Softmax，因此输出的所有目标概率和并不为0，$N_{\text{pos }}$为正样本的个数。
4. 定位损失采用的仍然是误差平方和的计算公式： L l o c ( l , g ) = ∑ i ∈ p o s ∑ m ∈ { x , y , w , h } ( l ^ i m − g ^ i m ) 2 N p o s L_{l o c}(l, g)=\frac{\sum_{i \in p o s} \sum_{m \in\{x, y, w, h\}}\left(\hat{l}_{i}^{m}-\hat{g}_{i}^{m}\right)^{2}}{N_{p o s}} Lloc​(l,g)=Npos​∑i∈pos​∑m∈{x,y,w,h}​(l^im​−g^​im​)2​$${\hat{l}}_i^x=\mathrm{Sigmoid}\left(t_x\right),{\hat{l}}_i^y=\mathrm{Sigmoid}\left(t_y\right)$$$${\hat{l}}_i^w=t_w,{\hat{l}}_i^h=t_h$$$${\hat{g}}_i^x=g_i^x-c_i^x,{\hat{g}}_i^y=g_i^y-c_i^y$$$${\hat{g}}_i^w=\ln \left(g_i^w/p_i^w\right),{\hat{g}}_i^h=\ln \left(g_i^h/p_i^h\right)$$

3.4 YOLO v3 SPP

YOLO v3 SPP是在YOLO v3基础上使用了很多Trick是的网络的mAP进一步的得到了提高，这里同样做一个记录看看网络是如何锦上添花的

3.4.1 关键知识点——Mosaic图像增强

我们通常使用的图像增强算法指的是图像随机裁剪、图像随机翻转、图像色度和饱和度的随机调整，而Mosaic图像增强指的是将图像进行随机拼接再输入到网络中进行训练，Mosaic图像增强的好处是：

1. 增加了数据的多样性；
2. 增加了目标的个数；
3. Batch Normalization能一次性统计多张图片的参数；

3.4.2 关键知识点——SPP模块

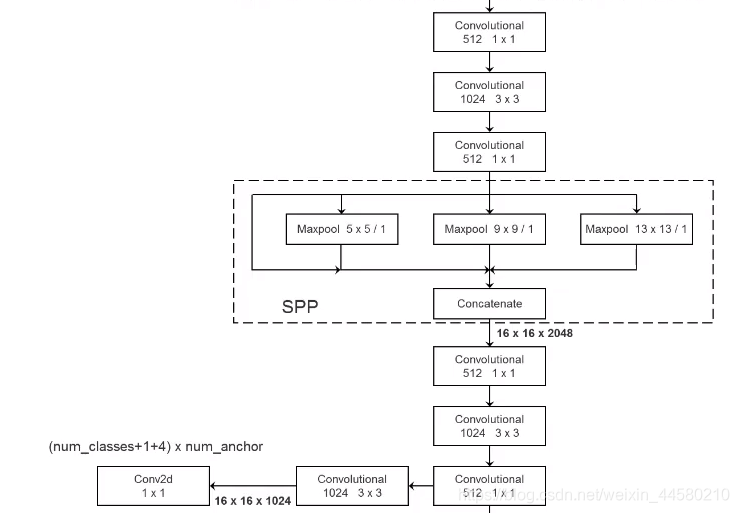
SPP模块的结构及位置如下图所示，就是将YOLO v3网络中的第一个预测特征中Convolutional Set拆开，在中间部分插入SPP结构：
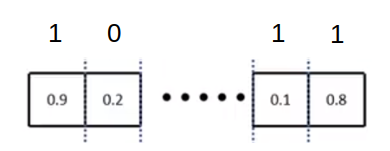
这里的SPP模块和SPPNet中的SPP结构（Spatial Pyramid Pooling）不同，SPP模块结构也相对简单，第一个分支是直连的，第二个分支为大小为$5\times 5$的最大池化下采样层，第三个分支大小为$9\times 9$d的最大池化下采样层，第四个分之为大小$13\times 13$的最大池化下采样层 ，四个分支最后通过Concatenate组合在一起，实现了不同尺度的特征融合，对于网络的mAP值会有明显的提升。

3.4.3 关键知识点——CloU Loss

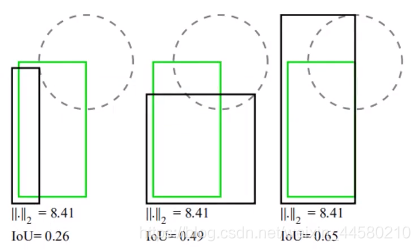
1. IoU Loss：在原始的YOLO v3网络中使用的定位损失计算公式为误差平方和损失，而这里剔除的CloU损失是一种基于IoU的损失计算方法，如下图所示
   
   其中绿色方框为真值，黑色方框为预测值，以上三种不同的结果如果计算误差平方和损失是一样的，这显然是不合理的，但是计算IoU就有明显不同，因为就有前辈提出IoU Loss，计算公式如下是：$$L_{IoU}=-\ln IoU$$通过这里例子我们就可以发现，IOU损失能够更好的反应重合程度并具有尺度不变形，但是缺点是不相交时损失为0.
2. GIoU Loss：为了解决这个问题，在IoU Loss的基础上又有人提出Generalized IoU，即GIoU，计算公式如下：$$GIoU=IoU-\frac{A^c-u}{A^c}$$$$L_{GIoU}=1-GIoU$$$$0\le L_{\text{GIoU }}\le 2$$其中$A^c$为下图中蓝色框区域，$u$为下图中红色加上绿色区域
   可以看出当两个边界框完全重合时，GIoU损失为0，当两个边界框相距无穷远时，GIoU损失为2，但是GIoU孙是同样拥有缺点，就是当预测边界框与真实边界框重合时，GIoU就退化为IoU。
3. DIoU Loss：在GIoU的基础上又进一步优化出来了Distance IoU，即DIoU，计算公式如下：$$DIoU=\mathrm{IoU}-\frac{{\rho }^2\left(b,b^{gt}\right)}{c^2}=\mathrm{IoU}-\frac{d^2}{c^2}$$$$L_{\text{DIoU }}=1-\text{ DIoU }$$$$0\le L_{DIoU}\le 2$$其中$c$为上图中蓝色方框对角线距离，$d$为上图中绿色方框与红色方框的中心点的距离，DIoU损失可以直接最小化两个边界框之间的距离，因此收敛速度更快。
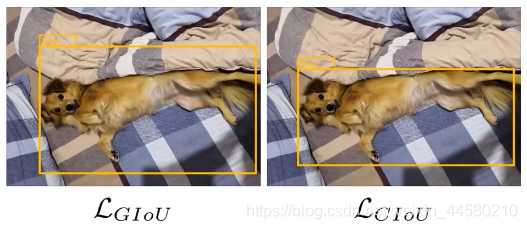
4. CIoU Loss：最后引出我们标题上的Complete IoU，即CIoU，计算公式如下：$$CIoU=\mathrm{IoU}-\left(\frac{{\rho }^2\left(b,b^{gt}\right)}{c^2}+\alpha v\right)$$$$v=\frac{4}{{\pi }^2}{\left(\arctan \frac{w^{gt}}{h^{gt}}-\arctan \frac{w}{h}\right)}^2$$$$\alpha =\frac{v}{(1-IoU)+v}$$$$L_{CIoU}=1-CIoU$$从公式可以看出来，相对DIoU，CIoU还多了一项$\alpha v$，这一项考虑了边界框的长宽比，如下图展示了分别使用GIoU和CIoU的检测结果
   

3.5 YOLO v4

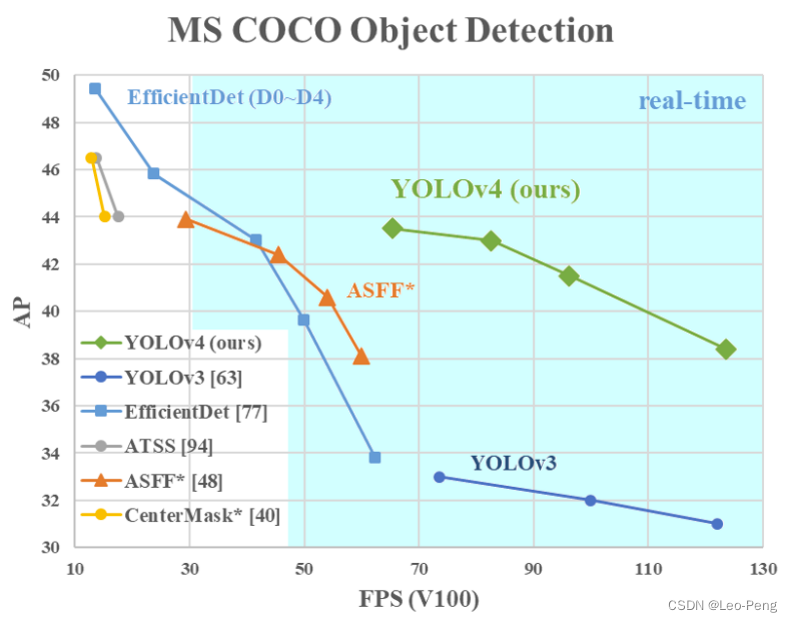
YOLO v4发表于2020年CVPR，从下图看YOLO v4相对于YOLO v3在精度和速度上都了骄傲的的提升，但是相对于YOLO v3 SPP提升并不大：

3.5.1 关键知识点——网络结构及特点

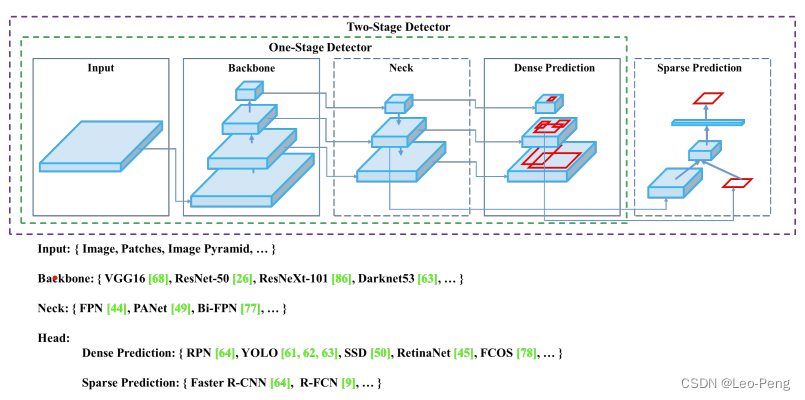
YOLO v4论文中对于目标检测网络进行了一个非常抽象的总结：

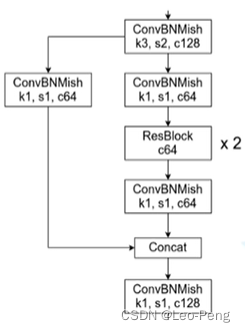
而YOLO v4使用的是CSPDarknet53作为Backbone，使用SPP，PAN结构作为Neck，使用YOLO v3结构作为Head。CSPDarknet53相对于YOLO v3使用的Darknet53主要是多了CSP结构，CSP结构是在论文CSPNet中提出的，结构如下图所示：

其中稍微特殊一点的就是Mish激活函数，Mish激活函数公式如下：$$\mathrm{Mish}(x)=x\times \tanh (\zeta (x))$$$$\tanh (x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$如果将Mish函数的图画出来可以看出来，其形状和我们常用的ReLU函数是基本一致的，都是无正向边界，可以避免梯度饱和。但不同的是Mish函数处处光滑，且再绝对值较小的负值区域允许一些负值存在。Mish激活函数计算复杂度比ReLU要高不少，如果计算资源不都可以考虑使用LeakyReLU代替Mish。论文中指出CSP结构的作用主要是：增强CNN的学习能力，减少计算的瓶颈以及减小显存的消耗。
PAN结构来自于论文Path Aggregation Network，Path Aggregation Network结构如下图所示：

所谓PAN结构指的就是图中(b)部分将FPN Backbone的输出由高分辨率像低分辨率再Aggregation一次。但是YOLO v4中稍有不同的是YOLO v4中PAN结构对特征进行拼接使用的是Concatente操作而不是Add操作。

3.5.2 关键知识点——优化策略

1. Eliminate Grid Sensitivity：在YOLO v2中，为了对网络预测的Bounding Box中心位置进行限制，将公式涉及为：$$b_x=\sigma \left(t_x\right)+c_x$$$$b_y=\sigma \left(t_y\right)+c_y$$
   其中$t_x,t_y$为网络输出值，$\sigma$为Sigmoid函数，将网络的输出值限制在0到1之间，$c_x,c_y$为对应栅格左上角坐标。这样存在一个问题，假设我们预测的Bounding Box的中心恰好在栅格左上角，那么就要求网络输出的$t_x,t_y$为无穷大，这对网络其实是不友好的，为此，在YOLO v4中，作者将该公式修改为$$b_x=\left(\sigma \left(t_x\right)\cdot {\text{ scale }}_{xy}-\frac{{\text{ scale }}_{xy}-1}{2}\right)+c_x$$$$b_y=\left(\sigma \left(t_y\right)\cdot {\text{ scale }}_{xy}-\frac{{\text{ scale }}_{xy}-1}{2}\right)+c_y$$在主要的代码实现中，通常将${\text{ scale }}_{xy}$设置为2，此时网络输出加上Sigmoid函数函数后值域标变为$-0.5$到$1.5$，使得Bounding Box的中心位置更加容易回归到0和1这两个位置。

2. Moisic Data Augmentation：大概原理就是将不同场景的图片拼接到一起然后送入训练，这样以增加网络的多样性，如下图所示：
   

3. IoU Threshold：在原始YOLO v3论文中，在选取正负样本时对于将中心点所在栅格的所有Anchor与GroundTruth的左上角对齐计算IoU，每个栅格只将与GroundTruth具备最大IoU的Anchor设置为正样本，这样会导致在训练过程中正样本的数据偏少。
   在YOLO v3 SPP中，将该正样本策略修改为了当IoU大于某个阈值时就为正样本，不再局限时最大的那个，这样可以使得正样本数量更多。
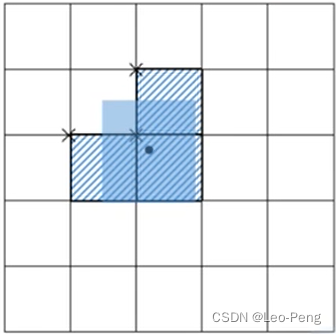
   而在YOLO v4中，作者将该策略进一步优化，根据上文介绍的中心点回归公式，$b_x$和$b_y$的输出范围都是$-0.5$到1.5，那么当GroundTruth的上左半区时，那么该栅格的上方和左侧的栅格都是有能力预测该真值的，因此这三个栅格中满足IoU阈值的Anchor都会被作为正样本，如下图所示：
   
   对于其他半区都是一样的，当GroundTruth正好落在该栅格的正中央时，那么就只取该栅格内满足IoU的Anchor。

4. Optimizered Anchors：YOLO v4中Anchor尺寸和YOLO v3稍有不同，这里不展开

5. CIOU：这部分内容读者可以参考上文介绍的SP中的内容。

3.6 YOLO v5

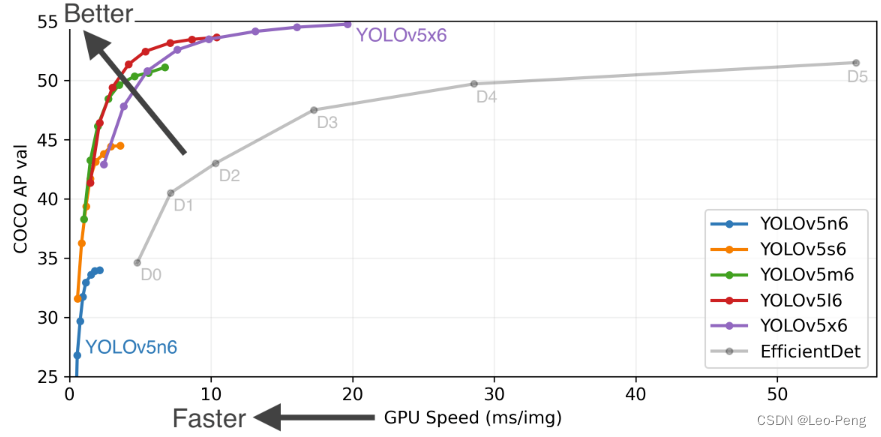
YOLO v5是一个Github项目，并没有参考的论文，但是YOLO v5取得了不错的效果，如下图所示，以EfficientDet为例，YOLO v5的效果要要远好于YOLO v4

3.6.1 关键知识点——网络结构及特点

YOLO v5使用的是New CSP-Darknet53作为Backbone，使用SPPF和New CSP-PAN作为Neck，使用YOLO v3 Head作为Head。SPPF是将原始$9\times 9$和$13\times 13$的MaxPool换成两个和三个$5\times 5$的MaPool的串联输出，这样最终输出的结果是一样的，但是效率会更高。

3.6.2 关键知识点——训练策略

1. Multi-scale Training：将训练数据进行随机缩放变换，缩放比例为$0.5$到$1.5$之间。
2. AutoAnchor(For training custom data)：可以从训练数据中聚类出新的Anchor参数。
3. Warmup and Cosine LR scheduler：该策略是再训练初期设置学习率由小逐渐变大，达到最大学习率后再以Cosine的变化趋势逐渐变小。
4. EMA(Exponential Moving Average)：该策略主要是给学习率加上一个动量，使得训练更加平滑。M
5. Mixed precision：即混合精度训练，可以降低显存占用并加快训练速度。

3.6.3 关键知识点——降低Grid敏感度

在YOLO v4中通过将中心点的归回公式修改如下公式进而降低了中心点回归对于Grid的敏感度：$$b_x=\left(\sigma \left(t_x\right)\cdot {\text{ scale }}_{xy}-\frac{{\text{ scale }}_{xy}-1}{2}\right)+c_x$$$$b_y=\left(\sigma \left(t_y\right)\cdot {\text{ scale }}_{xy}-\frac{{\text{ scale }}_{xy}-1}{2}\right)+c_y$$而在YOLO v5中，作者进一步将高度和宽度的回归公式由$$b_w=p_w\cdot e^{t_w}$$$$b_h=p_h\cdot e^{t_{\hslash }}$$修改为：$$b_w=p_w\cdot {\left(2\cdot \sigma \left(t_w\right)\right)}^2$$$$b_h=p_h\cdot {\left(2\cdot \sigma \left(t_h\right)\right)}^2$$该修改避免原公式中$t_x$和$t_y$过大进而导致的指数爆炸情况，进而出现训练出现Nan或者不稳定的情况。

4. FPN系列

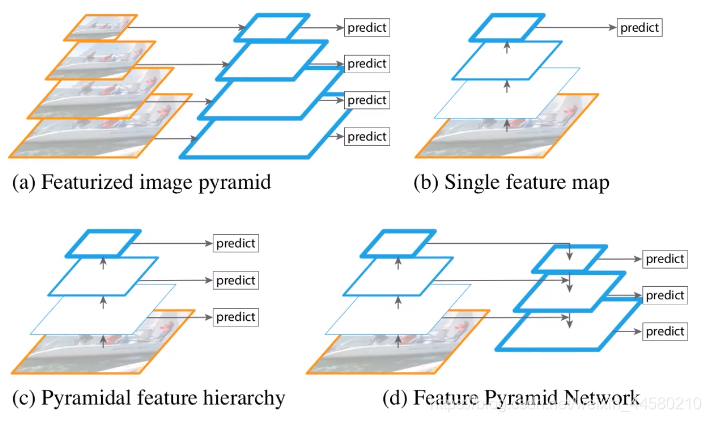
FPN是Feature Pyramid Networks的简称，下图展现了FPN结构与其他网络结构的区别，如下图为四种不同的类金字塔网络结构：

1. 图（a）为图像特征金字塔，即在不同尺度图像上生成特征层再进行目标检测，该结构的缺点就是计算量巨大。
2. 图（b）为Faster RCNN的简化结构图，即通过BackBone网络提取特征，并在最终的特征图上进行预测，该结构对于小目标的检测效果较差。
3. 图（c）的结构类似与SSD的网络结构，该网络同样会使用BackBone进行特征提取，但是会在BackBone的不同特征层上进行预测。
4. 图（d）就是本节要介绍的的FPN结构，该结构的特征就是对BackBone网络中的不同特征层进行融合再进行预测。

实验证明FPN结构能有效提高目标检测精度，除此之外，据我了解，Feature Pyramid结构其实除了在目标检测领域，在很多其他领域也能够起到提升性能的作用。

4.1 FPN

首先提出该结构的论文《Feature Pyramid Networks for Object Detection》发表于2016年的CVPR，在Fast RCNN网络基础上使用了FPN结构后，在cocoAP上提升2.3个点，在pascalAP上提升3.8个点。

4.1.1 关键知识点——网络结构与特点

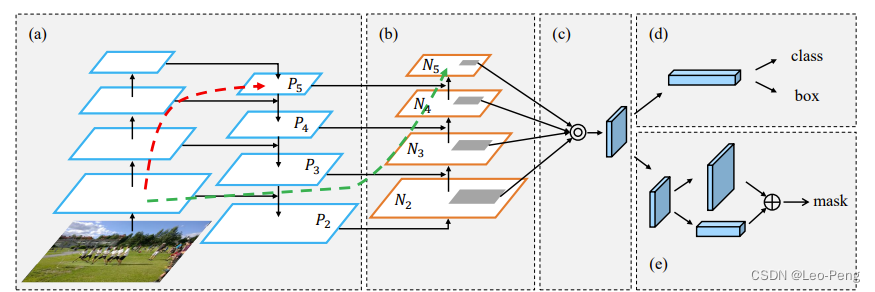
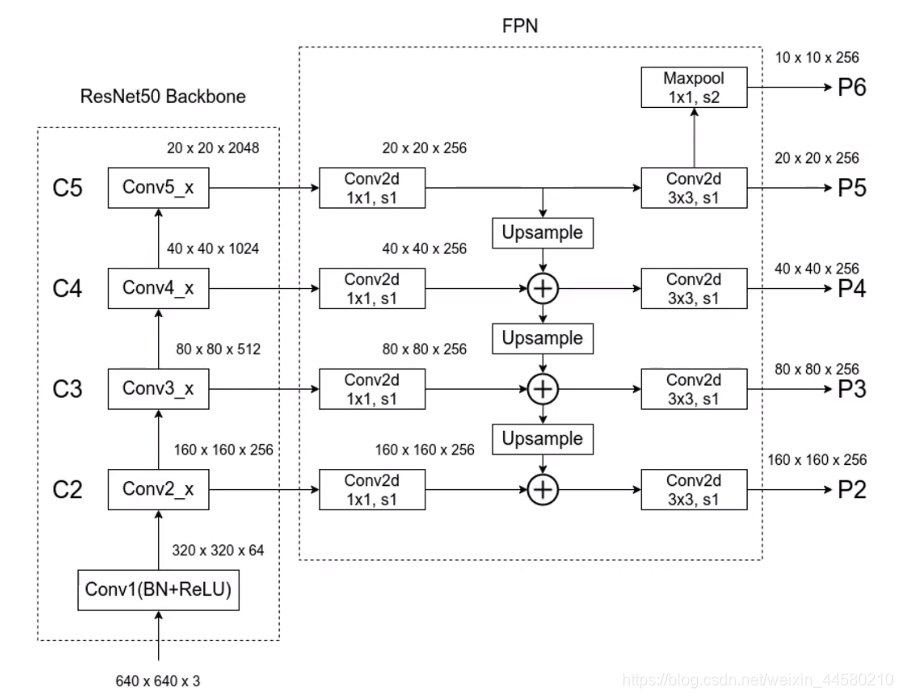
FPN网络中的细节如下，图片来源1.1.2 FPN结构详解：

如上图所示，

1. 网络的BackBone采用的是ResNet50；
2. 在上图右侧FPNj结构中，所有卷基层在进行融合之前都会先通过一个$1\times 1$的卷积层处理，目的就是为了使得不同特征层的Channel相同，然后高层的特征图需要进行2倍的上采样，目的是与低层的特征图达到同尺度然后进行融合，而融合方法就是对应通道的特征进行相加。
3. 网络运行是首先是通过RPN网络在P2-P6特征层上运行获得Proposal，然后在通过Fast RCNN网络获得最终的预测结果。对于不同的预测特征层，RPN和Fast RCNN的权重共享，也就是说使用同一个RPN网络和Fast RCNN网络在不同的特征层上获得预测结果。
4. 在原始的Faster RCNN网络中，是在相同的特征层上生成不同尺寸不同比例的Anchor，而在FPN网络中，在不同的特征层上对不同尺度的目标进行预测，换句话说，就是不同的特征层预测不同面积大小的物体，具体说来，一共有五种尺寸的Anchor分别是$\left\{32^2,64^2,128^2,256^2,512^2\right\}$分别对应 { P 2 , P 3 , P 4 , P 5 , P 6 } \left\{P_{2}, P_{3}, P_{4}, P_{5}, P_{6}\right\} {P2​,P3​,P4​,P5​,P6​}，每个尺寸都有 { 1 : 2 , 1 : 1 , 2 : 1 } \{1: 2,1: 1,2: 1\} {1:2,1:1,2:1}三种比例，因此在整个FPN网络中一种有15中不同的Anchor。

4.2 RetinaNet

RetinaNet的原论文为《Focal Loss for Dense Object Detection》，发表于2017年的CVPR上，其代表One-Stage网络首次超越Two-Stage网络，RetinaNet就是在FPN网络上的进一步升级。

4.2.1 关键知识点——网络结构及特点

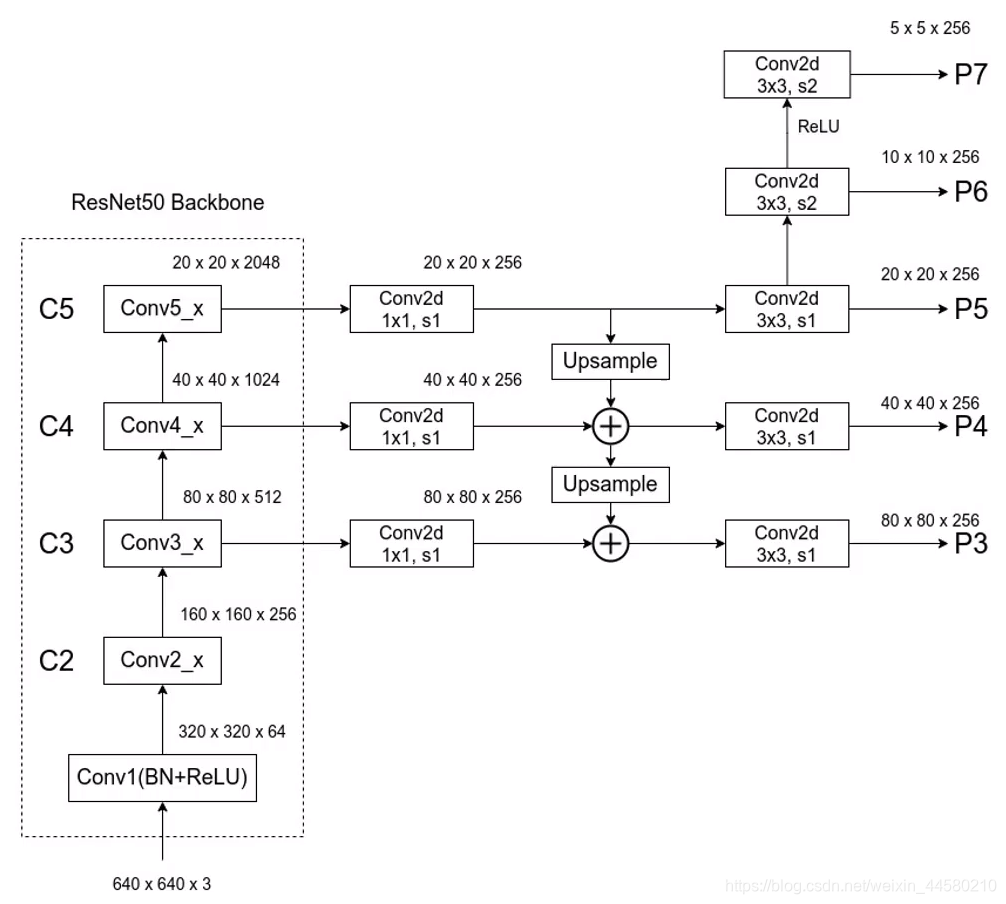
RetinaNet的网络结构如下：

与FPN网络中不同之处主要有如下几点

1. FPN结构中减少了P2层，由于P2层输出的特征层的维度较大，因此论文认为P2层占用了较大的计算资源，因此论文去掉了P2层，最大维度的特征层为P3层
2. P6层在FPN网络中是通过$1\times 1$的最大池化下采样层获得的，而在RetinaNet网络中是通过卷积层获得；
3. RetinaNet中增加了P7层用于检测更大的目标。
4. 在FPN网络中同一种尺度下三种比例的的Anchar，而在Retina网络中，一共有三种尺度对应三种比例，在ReitinaNet网络中一共有$32\left\{2^0,2^{\frac{1}{3}},2^{\frac{2}{3}}\right\}$，$64\left\{2^0,2^{\frac{1}{3}},2^{\frac{2}{3}}\right\}$，$128\left\{2^0,2^{\frac{1}{3}},2^{\frac{2}{3}}\right\}$，$256\left\{2^0,2^{\frac{1}{3}},2^{\frac{2}{3}}\right\}$，$512\left\{2^0,2^{\frac{1}{3}},2^{\frac{2}{3}}\right\}$共15中尺深度，每个尺寸同样对应 { 1 : 2 , 1 : 1 , 2 : 1 } \{1: 2,1: 1,2: 1\} {1:2,1:1,2:1}三种比例。

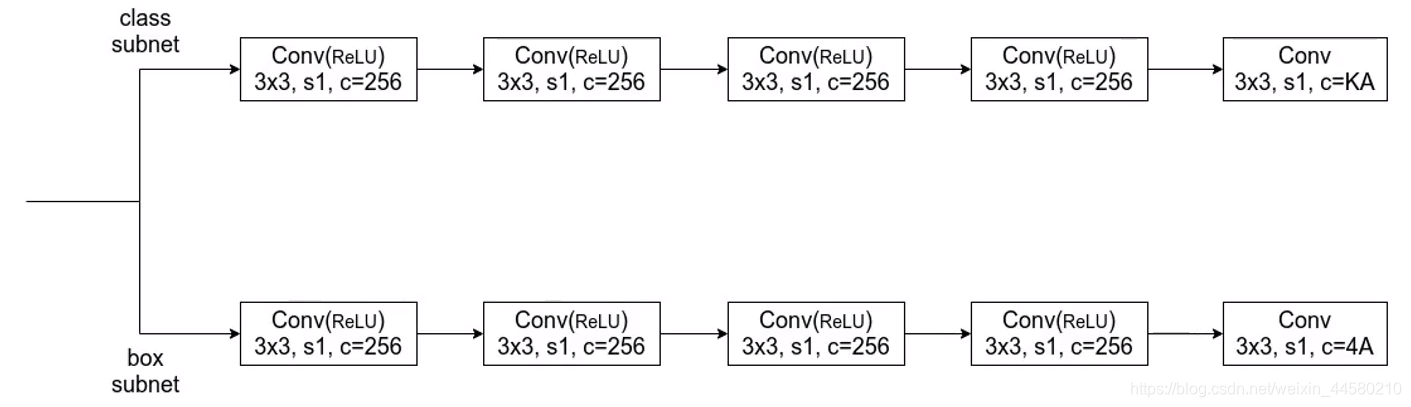
对于每个特征层，都会对应同一个预测器，注意不同层特征层之间的预测器权值共享，预测器的结构如下图所示：

1. 预测器中一共有两个分之，一个负责检测类别，每个Anchor预测$K$个物体类别，一个负责检测边界框位置，每个Anchor预测$4$个和位置相关的参数。

4.2.2 关键知识点——Focal Loss

在RetinaNet中除了网路结构外，最终的一个部分就是Focal Loss的计算了，这一点在标题中就已经体现出来了，Focal Loss的提出主要是为了解决One Stage网络中经常遇到的正负样本不匹配的问题，对于普通的交叉熵损失计算公式如下：$$\mathrm{CE}(p,y)=\{\begin{array}{ll}-\log (p)& \text{ if }y=1\\ -\log (1-p)& \text{ otherwise. }\end{array}$$为了表示简单，我们可以令$$p_{\mathrm{t}}=\{\begin{array}{ll}p& \text{ if }y=1\\ 1-p& \text{ otherwise }\end{array}$$因此二值交叉熵损失可以重写为$$\mathrm{CE}(p,y)=\mathrm{CE}\left(p_{\mathrm{t}}\right)=-\log \left(p_{\mathrm{t}}\right)$$所谓Focal Loss就是引入一个$\alpha$因子，对于正样本采用的系数为$\alpha$，对于负样本采用的是$1-\alpha$，我们进一步重写为$$\mathrm{CE}\left(p_{\mathrm{t}}\right)=-{\alpha }_{\mathrm{t}}\log \left(p_{\mathrm{t}}\right)$$进一步地，我们引入一个新的因子${\left(1-p_{\mathrm{t}}\right)}^{\gamma }$，那么最终Focal Loss的计算公式为：$$\mathrm{FL}\left(p_{\mathrm{t}}\right)=-{\left(1-p_{\mathrm{t}}\right)}^{\gamma }\log \left(p_{\mathrm{t}}\right)$$在上文中，$alpha$是一个超参数，并不能区分哪些是适合用来训练的样本，而${\left(1-p_{\mathrm{t}}\right)}^{\gamma }$这个因子能够降低容易区分的样本的损失贡献，而增强困难区分的样本的损失。如下图所示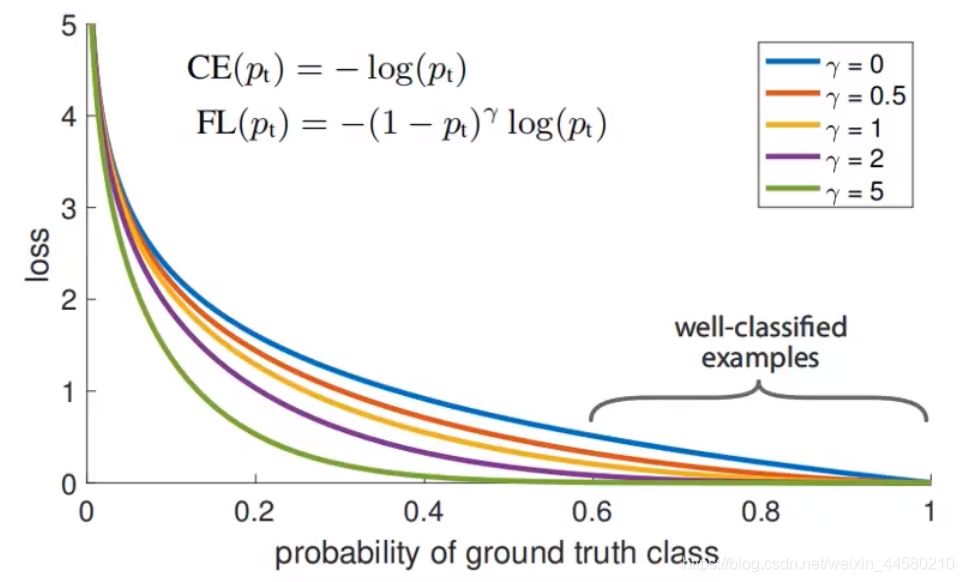：从上图可以看出来，当$\gamma$不等于零时，概率为0.6-1的这些高概率类别获得的损失相应减小，这样网络就可以将更多的资源应用到区分难以区分的类别上。以上大概就是Focal Loss的基本思想。

如上就完成了计算机网络中目标检测网络的流水账式的学习，再一次感谢Up主霹雳吧啦Wz，以上论文并没有时间去仔细阅读论文，仅仅是根据霹雳吧啦Wz的学习视频过了一遍，以后有用到的时候再去仔细研究。如果文章中有理解不对之处还请大家多多指出。