多视图几何总结——从本质矩阵恢复摄像机矩阵

本质矩阵是归一化坐标下基本矩阵的特殊形式，具有五个自由度，我们通过八点法或者五点法可以求出本质矩阵，那么我们如何从中恢复出我们实际想要的$R$和$t$呢？我们得从性质入手。

（1）本质矩阵性质

多视图几何上定义：一个3×3的矩阵是本质矩阵的充要条件是它的奇异值中有两个相等而第三个是0，为什么呢？
首先我们知道$$E=[t{]}_{\times }R=SR$$其中S为反对称矩阵，反对称矩阵有什么性质呢？

结论1：如果$S$是实的反对称矩阵，那么$S=UB{U}^T$，其中$B$为形如$diag(a_{1}Z，a_{2}Z...a_{m}Z，0，0...0)$的分块对角阵，其中$Z=\left[\begin{array}{cc}0& 1\\ -1& 0\end{array}\right]$，反对称矩阵的特征矢量都是纯虚数并且奇数阶的反对称矩阵必是奇异的

那么根据这个结论我们可以将$S$矩阵写成$\mathrm{S}=k{\mathrm{U}\mathrm{Z}\mathrm{U}}^{\top }$，而$\mathrm{Z}$为$$\mathrm{Z}=\left[\begin{array}{ccc}0& 1& 0\\ -1& 0& 0\\ 0& 0& 0\end{array}\right]$$而$Z$由可以写成$\mathrm{Z}=\mathrm{diag}(1,1,0)\mathrm{W}$，其中$\mathrm{W}$为$$\mathrm{W}=\left[\begin{array}{ccc}0& -1& 0\\ 1& 0& 0\\ 0& 0& 1\end{array}\right]$$因此这个$E$矩阵可以分解为$$\mathrm{E}=\mathrm{S}\mathrm{R}=\mathrm{U}\mathrm{diag}(1,1,0)\left({\mathrm{W}\mathrm{U}}^{\top }\mathrm{R}\right)$$这样就证明了$E$拥有两个相等的奇异值

（2）从本质矩阵恢复摄像机矩阵

假定第一个摄像机矩阵是$\mathrm{P}=[\mathrm{I}|0]$，为了计算第二个摄像机矩阵${\mathrm{P}}^{\prime }$，必须把$E$矩阵分解为反对成举着和旋转矩阵的乘积$\mathrm{S}\mathrm{R}$。
还是根据上面的结论一，我们在相差一个常数因子的前提下有$\mathrm{S}=\mathrm{U}{\mathrm{Z}\mathrm{U}}^{\mathrm{T}}$，我们假设旋转矩阵分解为${\mathrm{U}\mathrm{X}\mathrm{V}}^{\mathrm{T}}$，则有$$\mathrm{U}\mathrm{diag}(1,1,0){\mathrm{V}}^{\mathrm{T}}=\mathrm{E}=\mathrm{S}\mathrm{R}=\left({\mathrm{U}\mathrm{Z}\mathrm{U}}^{\mathrm{T}}\right)\left({\mathrm{U}\mathrm{X}\mathrm{V}}^{\top }\right)=\mathrm{U}(\mathrm{Z}\mathrm{X}){\mathrm{V}}^{\mathrm{T}}$$则有$\mathrm{Z}\mathrm{X}=\mathrm{diag}(1,1,0)$，因此$\mathrm{x}=\mathrm{W}$或者$\mathrm{X}={\mathrm{W}}^{\mathrm{T}}$

结论：如果$E$的SVD分解为$\mathrm{U}\mathrm{diag}(1,1,0){\mathrm{V}}^{\top }$，$\mathrm{E}=\mathrm{S}\mathrm{R}$有两种分解形式，分别是：$$\mathrm{S}={\mathrm{U}\mathrm{Z}\mathrm{U}}^{\top }\mathrm{R}={\mathrm{U}\mathrm{W}\mathrm{V}}^{\mathrm{T}}{\text{or UW }}^{\mathrm{T}}{\mathrm{V}}^{\top }$$

接着分析，又因为$\mathrm{S}\mathrm{t}=0$（自己和自己叉乘肯定为0嘛）以及$\Vert \mathbf{t}\Vert =1$（对两个摄像机矩阵的基线的一种常用归一化），因此$\mathbf{t}=\mathrm{U}(0,0,1{)}^{\mathrm{T}}={\mathbf{u}}_3$，即矩阵$U$的最后一列，这样的好处是不用再去求$S$了，应为$\mathbf{t}$的符号不确定，$R$矩阵有两种可能，因此其分解有如下四种情况：$${\mathrm{P}}^{\prime }=\left[{\mathrm{U}\mathrm{W}\mathrm{V}}^{\mathrm{T}}|+{\mathbf{u}}_3\right]\text{ or }\left[{\mathrm{U}\mathrm{W}\mathrm{V}}^{\mathrm{T}}|-{\mathbf{u}}_3\right]or\left[{\mathrm{U}\mathrm{W}}^{\mathrm{T}}{\mathrm{V}}^{\mathrm{T}}|+{\mathbf{u}}_3\right]\text{ or }\left[{\mathrm{U}\mathrm{W}}^{\mathrm{T}}{\mathrm{V}}^{\mathrm{T}}|-{\mathbf{u}}_3\right]$$
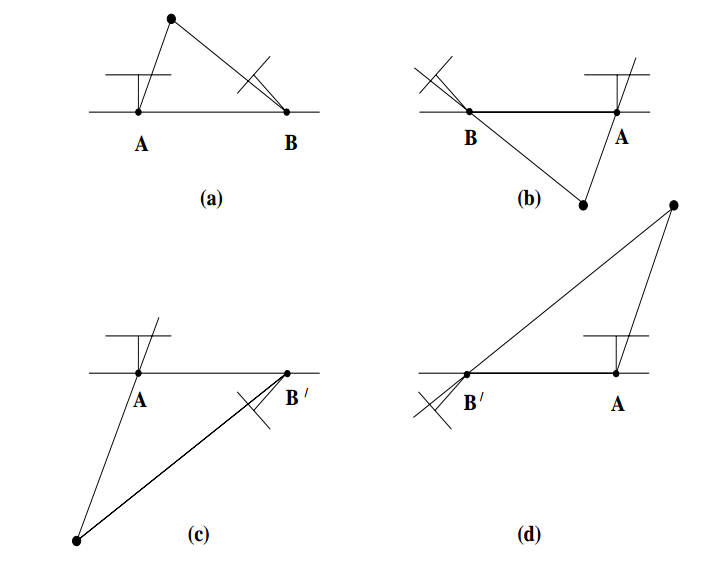
就是下面这张图展示的

然后用空间中的一个点作测试，验证它是否在两个摄像机前面就可以从两个不同解中确定一个作为摄像机矩阵

到这里就OK啦，有问题欢迎交流～

此外，对SLAM算法感兴趣的同学可以看考我的博客SLAM算法总结——经典SLAM算法框架总结