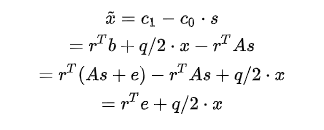前言
同学做了个隐私计算的分享,对其中恶意模型的同态加密有点感兴趣,做个简单的了解。由于只是简单了解,所以下面内容大多是拼凑,也不会有太深入的研究(毕竟笔者也是边学边做个记录XD)
一、概述
1、基本概念
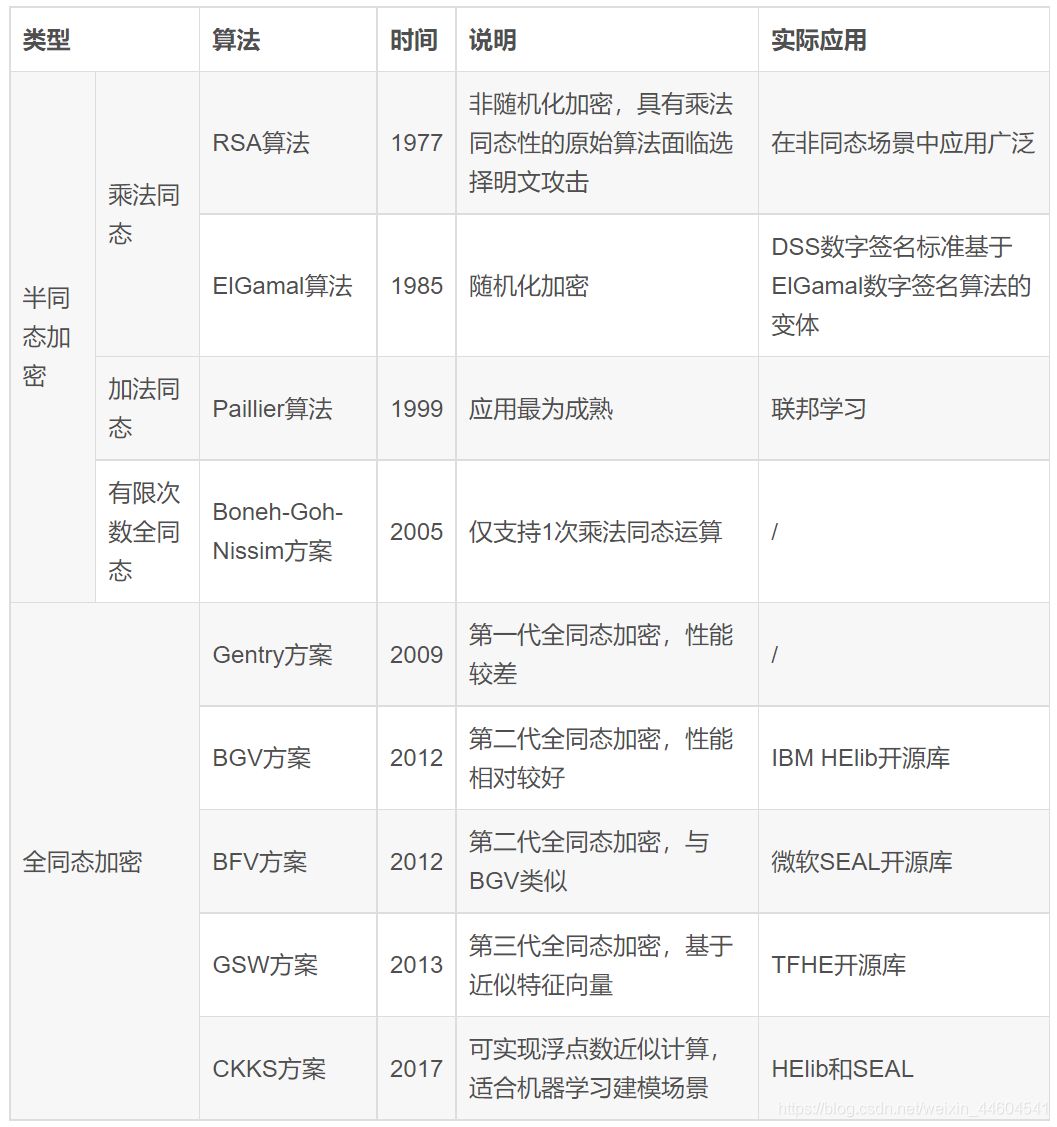
同态加密(Homomorphic Encryption, HE)是指满足密文同态运算性质的加密算法,即数据经过同态加密之后,对密文进行特定的计算,得到的密文计算结果在进行对应的同态解密后的明文等同于对明文数据直接进行相同的计算,实现数据的“可算不可见”
- 如果满足 f(A)+f(B)=f(A+B)f(A)+f(B)=f(A+B) , 我们将这种加密函数叫做加法同态
- 如果满足 f(A)×f(B)=f(A×B)f(A)×f(B)=f(A×B) ,我们将这种加密函数叫做乘法同态。
如果一种同态加密算法支持对密文进行任意形式的计算(即满足加法和乘法),则称其为全同态加密(Fully Homomorphic Encryption, FHE);如果支持对密文进行部分形式的计算,例如仅支持加法、仅支持乘法或支持有限次加法和乘法,则称其为半同态加密或部分同态加密,英文简称为SWHE(Somewhat Homomorphic Encryption)或PHE(Partially Homomorphic Encryption)
目前,同态加密算法已在区块链、联邦学习等存在数据隐私计算需求的场景实现了落地应用。由于全同态加密仍处于方案探索阶段,现有算法存在运行效率低、密钥过大和密文爆炸等性能问题,在性能方面距离可行工程应用还存在一定的距离。因此,实际应用中的同态加密算法多选取半同态加密(如加法同态),用于在特定应用场景中实现有限的同态计算功能。
2、研究进展
同态加密(Homomorphic Encryption)是很久以前密码学界就提出来的一个Open Problem。早在1978年,Ron Rivest, Leonard Adleman, 以及Michael L. Dertouzos就以银行为应用背景提出了这个概念[RAD78],Ron Rivest和Leonard Adleman分别就是著名的RSA算法中的R和A
二、大致原理
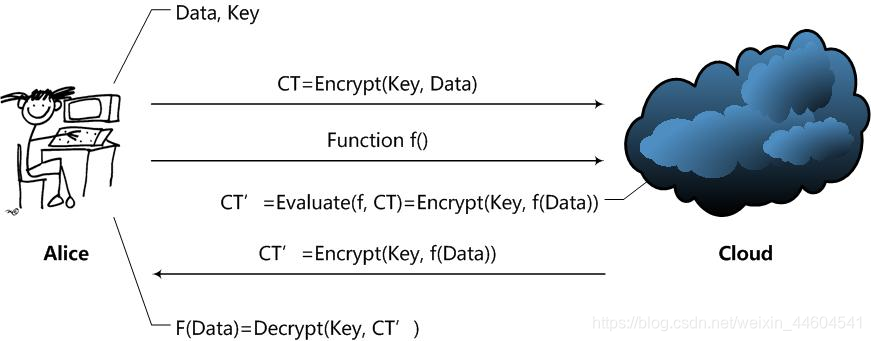
Alice通过Cloud,以Homomorphic Encryption(以下简称HE)处理数据的整个处理过程大致是这样的:
- Alice对数据进行加密,把加密后的数据发送给Cloud
- Alice向Cloud提交数据的处理方法,这里用函数f来表示
- Cloud在函数f下对数据进行处理,并且将处理后的结果发送给Alice
- Alice对数据进行解密,得到结果
据此,我们可以很直观的得到一个HE方案应该拥有的函数:
- KeyGen函数:密钥生成函数。这个函数应该由Alice运行,用于产生加密数据Data所用的密钥Key。当然了,应该还有一些公开常数PP(Public Parameter)
- Encrypt函数:加密函数。这个函数也应该由Alice运行,用Key对用户数据Data进行加密,得到密文CT(Ciphertext)
- Evaluate函数:评估函数。这个函数由Cloud运行,在用户给定的数据处理方法f下,对密文进行操作,使得结果相当于用户用密钥Key对f(Data)进行加密
- Decrypt函数:解密函数。这个函数由Alice运行,用于得到Cloud处理的结果f(Data)
噪声处理办法Bootstrapping:
- 同态加密算法A对明文C1进行加密,获得密文S1,加密运算产生噪声
- 使用同态加密算法B,对密文S1加密得到S2,S2上执行加密系统A的解密算法,
消除噪声,获得加密后的明文C2。 - 使用同态加密算法B对C2再执行加密系统A的加密算法,再用B的解密算法解密
三、分类概要
1、部分同态加密(Partially Homomorphic Encryption)
只有一种同态加密特性,加法同态或者乘法同态。
(1)EIGamal加密算法
基于循环群G,满足加法同态,循环群特性
(2)RSA算法
可以实现乘法同态
2、近似同态加密(Somewhat Homomorphic Encryption)
可以在密文上实现加法和乘法,但是次数非常有限
3、有限级数全同态加密
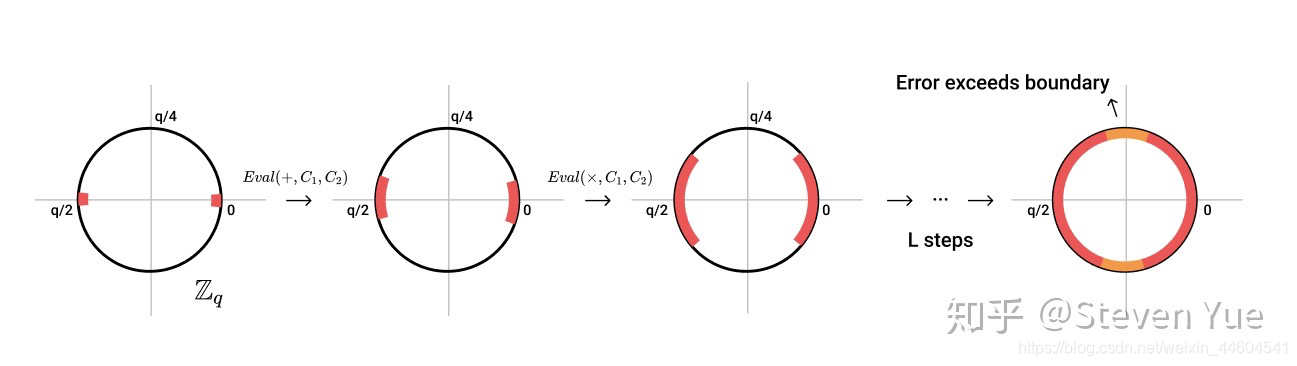
对密文可以进行任意的加法乘法组合了,对于次数没有局限性。但算法引入了复杂度上线L的概念,如果把函数F用二进制电路C来表示,那么C的深度和大小一定要在L的范围之内
|C| ≤ L
算法在加密的时候会在密文里加入一定的随机噪音,进行同态计算的时候,自带的噪音会被叠加扩大,如果过于堆叠密文,噪音超过临界值,就会覆盖掉原来的原文,解密会失败。
4、全同态加密
性质和属性:
- 正确性
- 语义安全
- 简短性
(1)第一代
理想格的假设
Gentry于09年提出了理想格的假设,并提出了Bootstrapping,能够对密文进行特殊处理,把一个噪音接近临界值的密文重新刷新成一个噪音很低的新密文。
(2)第二代
基于格加密的,另一种假设Learning With Errors(LWE)
BGV系统,一个有限级数的同态加密系统,但可以通过Bootstapping的方法变成全同态系统。
(3)第三代
GSW系统,本身具有有限级数全同态性质,基于更加简单的LWE假设,通过Bootstrapping可以达到全同态。
四、格密码学与LWE问题
1、格(Lattice)
(1)整数格的构造
描述一个线性空间V,使用一组基。拥有两个基向量b0,b1,那么任意一个向量都可以被分解为这两个基向量的任意线性组合。
v=c0b0+c1b1
这个线性空间就是b0,b1两个基向量的线性生成空间。
加上约束:如果线性组合系数ci都必须是整数。
向量会构成一个密布的、网格状的离散集合。 离散的基向量生成空间集合,称为整数格。
(2)新的问题
如果向量v是带小数的,就没有办法表达它,需要通过找到一组整数系数,使得向量v’距离目标向量v距离最近
在离散线性集合中逼近目标向量的问题,统称为最近向量问题 CVP,是非常难解决的(NP-hard)
2、LWE问题
(1)从CVP问题到LWE问题
线性代数中,Ax=b,矩阵A和向量b,可以找到另一个向量x,使得Ax=b。
当添加了噪音e之后,Ax+e=b,e是一个固定数值范围内随机采集的一个随机噪音向量。因为带了噪声,所以不能直接用高斯消除来逐个求解x。
如何带着误差还原向量,称为误差还原(Learning With Error, LWE)问题。
(2)LWE问题
参数详细说明
- 在一个LWE问题中,定义矩阵A的维度 mn,m代表了线性方程组一共有多少组方程,n代表每个方程中有多少个未知数
- 还需要定义整个有限域Zq的大小q,一般选择一个足够大的素数作为q
- 选择叠加的误差噪音的取值上限B,B的大小决定了我们找到的解距离实际取值b可以相差多少。
各个参数的改变情况
- n是LWE问题的安全参数,n越大整个问题越难
- m是n的一个多项式倍数,m=poly(n),可用的方程组越多,问题越简单
- q一般也是n的一个多项式倍数,一般设置q为O(n2)
- 误差上线B需要比q小很多很多,B<<q。误差越小的话,那么找到正确的解相对来说越简单
(3)决策LWE
决策LWE是指辨别一个b到底是误差乘积还是随机生成的向量,这也是一个困难问题。
五、GSW-LFHE系统
1、找同态
矩阵的特征值和特征向量可以形成线性关系:Ax=ax
密钥生成:随机选取一个向量s
加密算法:明文数字u,找到一个矩阵C,Cs=us。
解密算法:计算Cs,观察s的变化
运算算法:(C1+C2)s=(u1+u2)s;(C1C2)s=(u1u2)s
加密算法问题,可以根据C,简单找到C的特征向量和对应的特征值,再找出s和u。
2、加噪声
加入噪声e:Cs=us+e
密钥生成:选取一个随机向量s,向量最下面加上一个-1。
加密算法:生成一个随机矩阵A,对应的噪声向量e。C=(A,As+e)+uI,I是单位矩阵。
解密算法:Cs=((A,As+e)+uI)s=(A,As+e)s+uIs=As-(As+e)+us=us-e。
运算算法:(C1+C2)s=C1s+C2s=(u1+u2)s+(c1+c2) ,这时e1+e2仍然可以接受。(C1C2)s=C1(u2s+e2)=u1u2s+u2e1+C1e2,u2e1需要控制u2大小,C1e2需要控制C1大小。
3、加入二进制分解
针对u2,我们选择01比特,只能加密一个二进制。
针对C1,我们选择使用二进制分解,将原有的矩阵拆分成二进制矩阵表达,最后加一个2n矩阵。
密钥生成:同上
加密算法:u只能是二进制比特。加密过程与之前大致相似,在定义系数方面,需要维度相符。m=nlog(q)。
C=(A,As+e)+uG 这边G是二进制重组矩阵。最后输出的也是C的二进制分解态作为密文。
解密算法:CGs=Cs=uGs-e。
六、格密码学与Regev加密算法
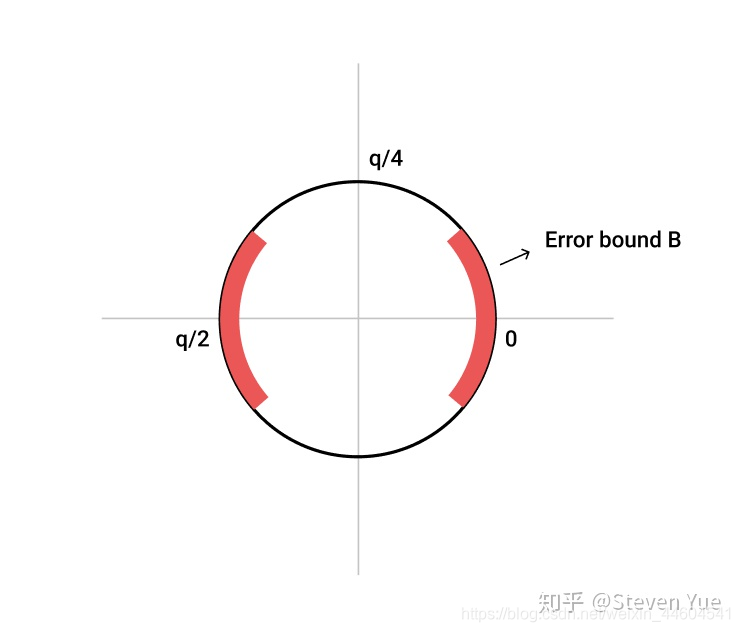
密钥生成部分很通用。算法中给出的B的选取条件q/4>mB需要注意。
密文生成部分,先选取一个随机数r,随后用r生成密文第一部分(矩阵),再加入x生成第二部分。
解密只需要计算出x即可,再看看|x|<q/4。
这个图可以很好地解释为什么是q/4。只要满足一定的噪声分布,就可以划归到相应的数据。
Regev的正确性很好解释,直接重新计算一遍即可
语义安全:语义安全就是看能否区分实际出现的密文和随机数。因为c0,c1都是选用随机数来生成(加入了随机数)。因此是很难区分随机数和密文。
结语
简单了解了下同态加密,并未深入研究
参考: