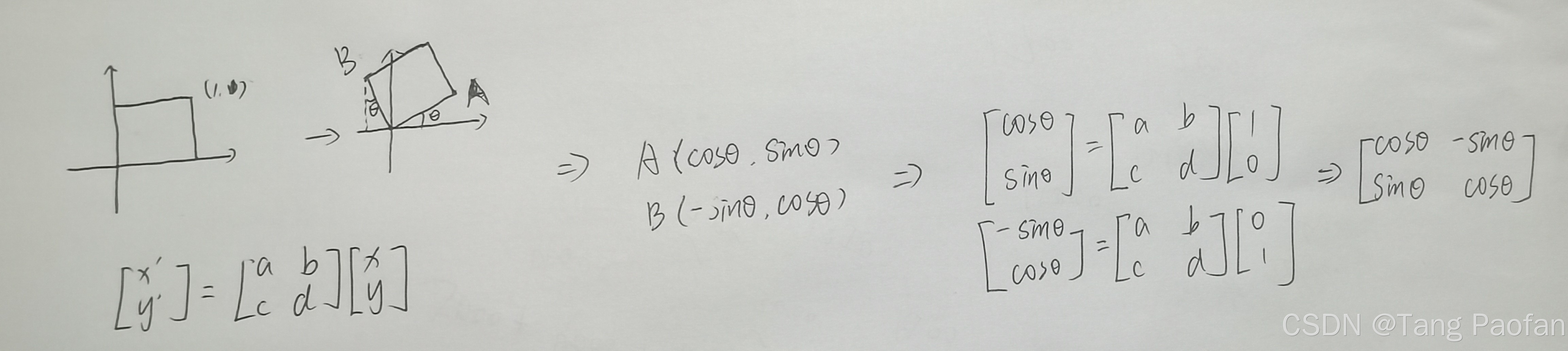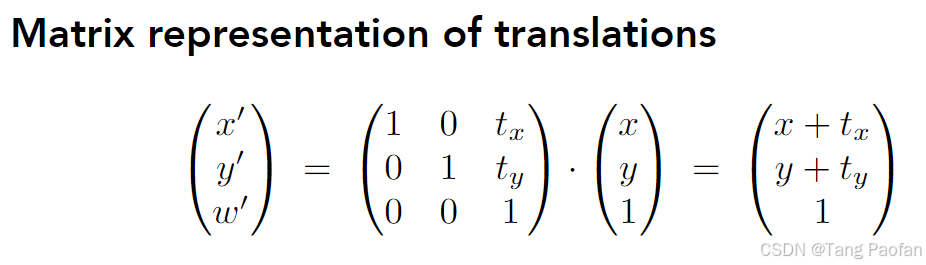概述
- 变换
- 为什么学习旋转
- 2维 变换
- Homogeneous coordinates(齐次坐标)
- 旋转、平移默认从原点开始
旋转分类
- 模型旋转
- 视图旋转(摄像机旋转)
二维线性变换
Scale(缩放)=>
x
,
=
s
x
x^,=sx
x,=sx
y
,
=
s
y
y^,=sy
y,=sy
缩放矩阵=>
[
x
,
y
,
]
=
[
s
0
0
s
]
[
x
y
]
\begin{bmatrix} x^, \\ y^, \end{bmatrix} = \begin{bmatrix} s & 0 \\ 0 & s\\ \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}
[x,y,]=[s00s][xy]
翻转矩阵=>
[
x
,
y
,
]
=
[
−
1
0
0
1
]
[
x
y
]
\begin{bmatrix} x^, \\ y^, \end{bmatrix} = \begin{bmatrix} -1 & 0 \\ 0 & 1\\ \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}
[x,y,]=[−1001][xy]
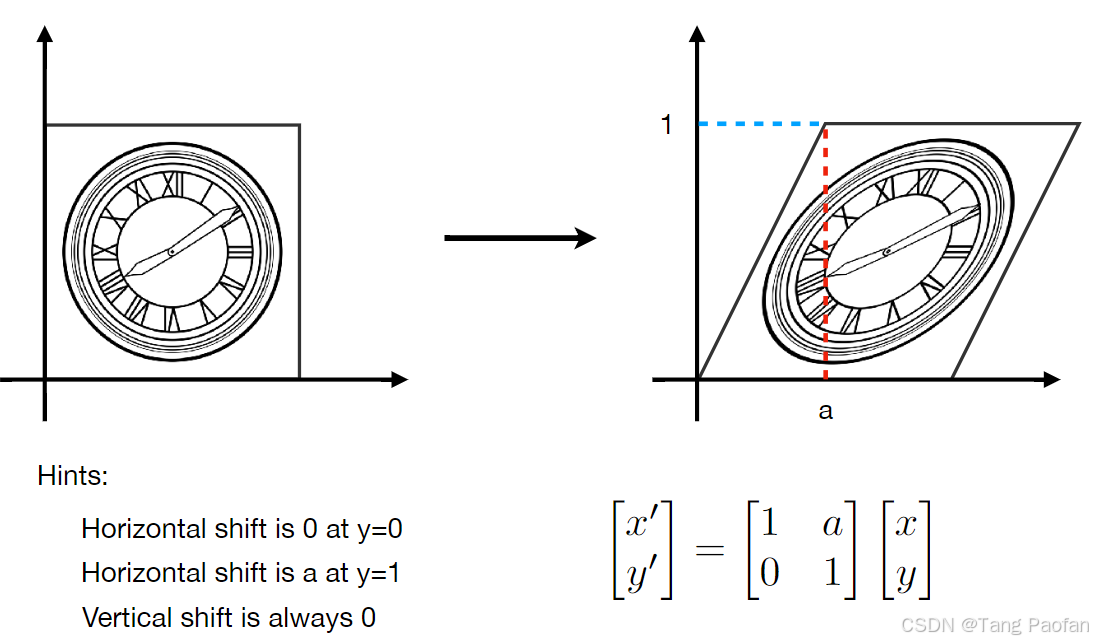
错切矩阵=>
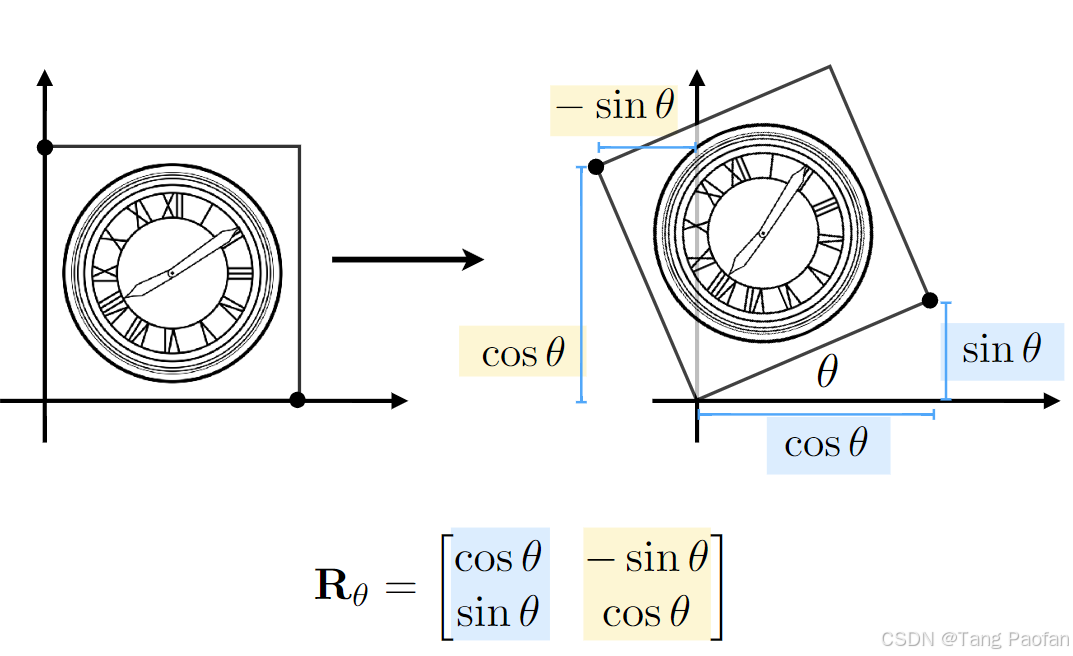
旋转矩阵=>
推导:
线性变换 Linear Transforms
[ x , y , ] = [ a b c d ] [ x y ] \begin{bmatrix} x^, \\ y^, \end{bmatrix} = \begin{bmatrix} a & b \\ c & d\\ \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} [x,y,]=[acbd][xy]
二维平移变换
x
,
=
x
+
t
x^, = x + t
x,=x+t
y
,
=
y
+
t
y^, = y + t
y,=y+t
=>
[
x
,
y
,
]
=
[
x
y
]
+
[
t
x
t
y
]
\begin{bmatrix} x^, \\ y^, \end{bmatrix}=\begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} t_x \\ t_y \end{bmatrix}
[x,y,]=[xy]+[txty]
但 [ x , y , ] = [ a b c d ] [ x y ] + [ t x t y ] \begin{bmatrix} x^, \\ y^, \end{bmatrix}=\begin{bmatrix} a & b \\ c & d\\ \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} t_x \\ t_y \end{bmatrix} [x,y,]=[acbd][xy]+[txty]不是线性变换,Is there a unified way to represent all transformations?->齐次坐标
齐次坐标(Homogenous Coordinates)
规定
2D point =
(
x
,
y
,
1
)
T
(x, y, 1)^T
(x,y,1)T
2D vector =
(
x
,
y
,
0
)
T
(x, y, 0)^T
(x,y,0)T
- 为什么2D point 齐次坐标最后是1
- 其实更加通用的形式为 ( x , y , w ) T = ( x / w , y / w , 1 ) T (x, y, w)^T = (x/w, y/w, 1)^T (x,y,w)T=(x/w,y/w,1)T
- 为什么2D vector齐次坐标最后是0
- 向量具有平移不变性,即平移后,仍表示同一个向量
当w是1or0时,如下有效
- vector + vector = vector
- point - point = vector
- point + vector = point
- ponit + point = point(中点)
仿射变换(Affine Transformations)
Affine map = linear map + translation
- 先线性变换
- 再平移
[ x , y , ] = [ a b c d ] [ x y ] + [ t x t y ] \begin{bmatrix} x^, \\ y^, \end{bmatrix}=\begin{bmatrix} a & b \\ c & d\\ \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} t_x \\ t_y \end{bmatrix} [x,y,]=[acbd][xy]+[txty]
齐次坐标表示=>
[ x , y , 1 ] = [ a b t x c d t y 0 0 1 ] [ x y 1 ] \begin{bmatrix} x^, \\ y^, \\ 1 \end{bmatrix}=\begin{bmatrix} a & b & t_x \\ c & d & t_y\\ 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} x,y,1 = ac0bd0txty1 xy1
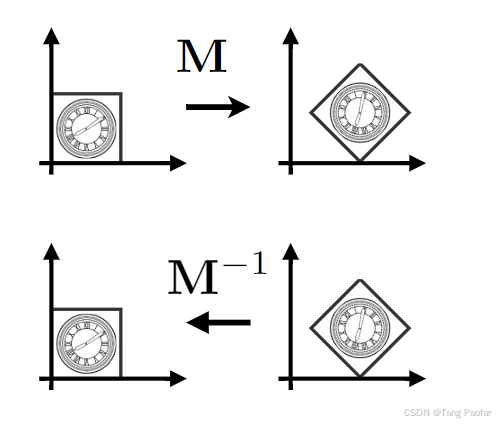
逆变换(Inverse Transform)
M
−
1
M^{-1}
M−1逆矩阵表示了逆变换
转换顺序
-
先旋转在平移≠先平移再旋转
-
矩阵应用顺序为从右到左
-
多个仿射变换时可合并为一个
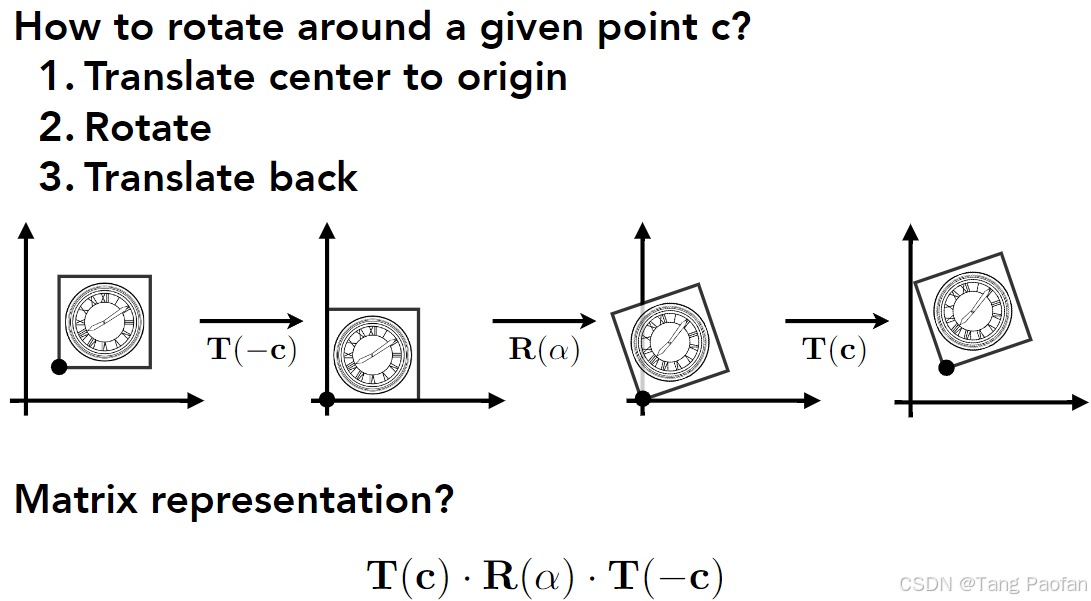
分解复杂变换
- 平移到圆心
- 旋转
- 平移回去