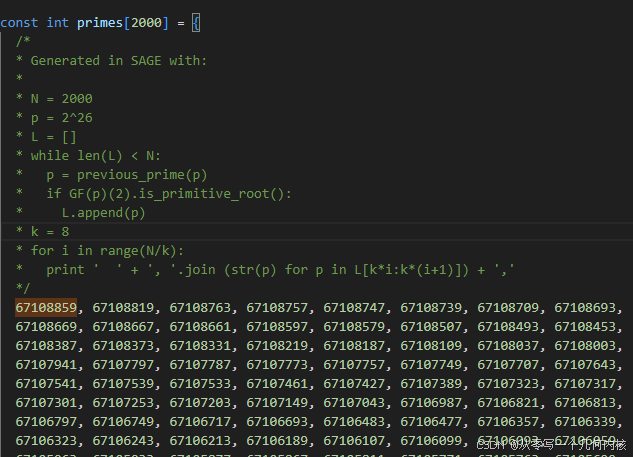
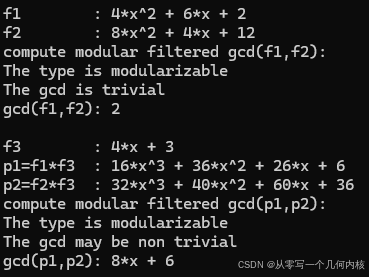
这部分主要涉及的是模运算,用于gcd,结式以及通过对素数取模构建过滤器避免不必要的计算,这是因为系数增长会导致gcd的计算成本增加。
基本概念
- IEEE 754标准
- 扩展精度浮点数 在一些处理器上,传统的FPU使用扩展的精度。但是在实现Residue类的时候需要尾数精度
- FPU 浮点运算单元
- 结式resultant 指由两个多项式的系数所构成的一种行列式,或称Sylvester行列式,结式可判断两个多项式是否有公根、是否互素,以及判断多项式是否有重根。
- 数论基础 里面包含了关于同余的定义
- 商群
- 有限域及Z/PZ
- 多项式的模运算
- 线性同余方程 CGAl代码中应用了扩展欧几里得算法进行求解
- 中国剩余定理
- 欧几里德算法
- 扩展欧几里德算法
- [环同态]ring homomorphism。
- 典范同态
c++概念
- unary_function cpp98里面常用,c++11弃用,但CGAL里面在“CGAL\functional.h”里面保留unary_function与binary_function。
- 函子
文档关键内容
-
CGAL在primes.h里面定义了primes[2000]素数数组便于计算,大小被限制为2e26,p的初始值为67108859。
-
Residue类就是有限域的实现
-
Modularizable
如果存在到基于类型CGAL::Residue的代数结构的合适映射。对于标量类型,例如整数,这个映射只是到CGAL::Residue的典范同态。对于复合类型,例如多项式,映射应用于复合类型的系数。
-
CGAL::Protect_FPU_rounding允许在计算区间算术运算序列时减少舍入模式变化的次数;CGAL::Protect_FPU_rounding pfr(CGAL_FE_TONEAREST)可以强制IEEE双精度和舍入模式到最接近
例子代码
#include <CGAL/config.h>
#include <iostream>
#include <CGAL/Gmpz.h>
#include <CGAL/Polynomial.h>
// Function in case Polynomial is Modularizable
template< typename Polynomial >
bool may_have_common_factor(
const Polynomial& p1, const Polynomial& p2, CGAL::Tag_true) {
std::cout << "The type is modularizable" << std::endl;
// Enforce IEEE double precision and rounding mode to nearest
// before using modular arithmetic
CGAL::Protect_FPU_rounding<true> pfr(CGAL_FE_TONEAREST);
// Use Modular_traits to convert to polynomials with modular coefficients
typedef CGAL::Modular_traits<Polynomial> MT;
typedef typename MT::Residue_type MPolynomial;
typedef typename MT::Modular_image Modular_image;
MPolynomial mp1 = Modular_image()(p1);
MPolynomial mp2 = Modular_image()(p2);
// check for unlucky primes, the polynomials should not lose a degree
typename CGAL::Polynomial_traits_d<Polynomial>::Degree degree;
typename CGAL::Polynomial_traits_d<MPolynomial>::Degree mdegree;
if (degree(p1) != mdegree(mp1)) return true;
if (degree(p2) != mdegree(mp2)) return true;
// compute gcd for modular images
MPolynomial mg = CGAL::gcd(mp1, mp2);
// if the modular gcd is not trivial: return true
if (mdegree(mg) > 0) {
std::cout << "The gcd may be non trivial" << std::endl;
return true;
}
else {
std::cout << "The gcd is trivial" << std::endl;
return false;
}
}
// This function returns true, since the filter is not applicable
template< typename Polynomial >
bool may_have_common_factor(
const Polynomial&, const Polynomial&, CGAL::Tag_false) {
std::cout << "The type is not modularizable" << std::endl;
return true;
}
template< typename Polynomial >
Polynomial modular_filtered_gcd(const Polynomial& p1, const Polynomial& p2) {
typedef CGAL::Modular_traits<Polynomial> MT;
typedef typename MT::Is_modularizable Is_modularizable;
// Try to avoid actual gcd computation
if (may_have_common_factor(p1, p2, Is_modularizable())) {
// Compute gcd, since the filter indicates a common factor
return CGAL::gcd(p1, p2);
}
else {
typename CGAL::Polynomial_traits_d<Polynomial>::Univariate_content content;
typename CGAL::Polynomial_traits_d<Polynomial>::Construct_polynomial construct;
return construct(CGAL::gcd(content(p1), content(p2))); // return trivial gcd
}
}
测试代码
CGAL::IO::set_pretty_mode(std::cout);
typedef CGAL::Gmpz NT;
typedef CGAL::Polynomial<NT> Poly;
CGAL::Polynomial_traits_d<Poly>::Construct_polynomial construct;
Poly f1 = construct(NT(2), NT(6), NT(4));
Poly f2 = construct(NT(12), NT(4), NT(8));
Poly f3 = construct(NT(3), NT(4));
std::cout << "f1 : " << f1 << std::endl;
std::cout << "f2 : " << f2 << std::endl;
std::cout << "compute modular filtered gcd(f1,f2): " << std::endl;
Poly g1 = modular_filtered_gcd(f1, f2);
std::cout << "gcd(f1,f2): " << g1 << std::endl;
std::cout << std::endl;
Poly p1 = f1 * f3;
Poly p2 = f2 * f3;
std::cout << "f3 : " << f3 << std::endl;
std::cout << "p1=f1*f3 : " << p1 << std::endl;
std::cout << "p2=f2*f3 : " << p2 << std::endl;
std::cout << "compute modular filtered gcd(p1,p2): " << std::endl;
Poly g2 = modular_filtered_gcd(p1, p2);
std::cout << "gcd(p1,p2): " << g2 << std::endl;
结果
源码部分截图
template< class COEFF >
class Modular_traits< Polynomial<COEFF> > {
private:
typedef Modular_traits<COEFF> Mtr;
public:
typedef Polynomial<COEFF> NT;
typedef Modular_traits<NT> Self;
typedef typename Mtr::Is_modularizable Is_modularizable;
typedef Polynomial<typename Mtr::Residue_type> Residue_type;
struct Modular_image{
Residue_type operator()(const NT& p){
std::vector<typename Mtr::Residue_type> V;
typename Mtr::Modular_image modular_image;
for(int i=0; i<=p.degree();i++)
V.push_back(modular_image(p[i]));
return Residue_type(V.begin(),V.end());
}
};
struct Modular_image_representative{
NT operator()(const Residue_type& p) const {
std::vector<COEFF> V;
typename Mtr::Modular_image_representative modular_image_representative;
for(int i=0; i<=p.degree();i++)
V.push_back(modular_image_representative(p[i]));
return NT(V.begin(),V.end());
}
};
};
可以清楚的看到Modular_traits的作用,Modular_image对于多项式Polynomial将参数传入utd::vector转成Residue_type格式返回