SVM算法

SVM:支持向量机

目的:解决感知机的问题

感知机问题:

1.泛化能力弱

2.只关注错误点,不考虑各类别的分布,就会出现过拟合

一:SVM介绍

1.svm思想

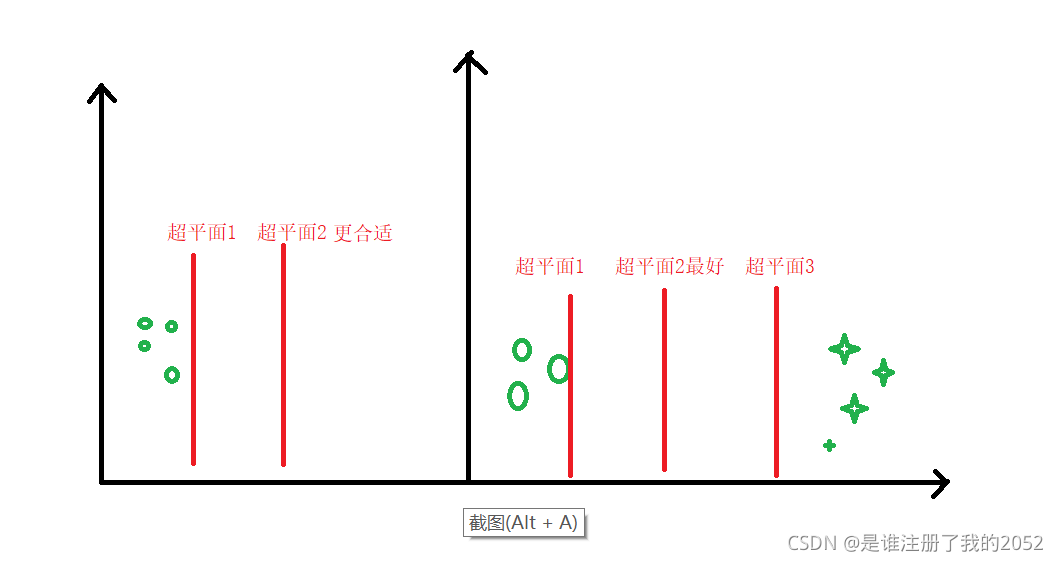
数据集中的点在分割之后离超平面越远越好

分割:理解为函数 f

超平面:理解为参数W , 决定函数的集合

分割和超平面理解为: f(W)

越远越好:

• 越远则预留的空间越大,可以容纳更多新的数据点,解决泛化能力
• 多个类别的时候要综合考虑类与类之间的距离
  

二.SVM模型

需要解决两个问题:

1.距离计算 max[marg(Wi,Xi)]

2.s.t 前提:所有分类都正确

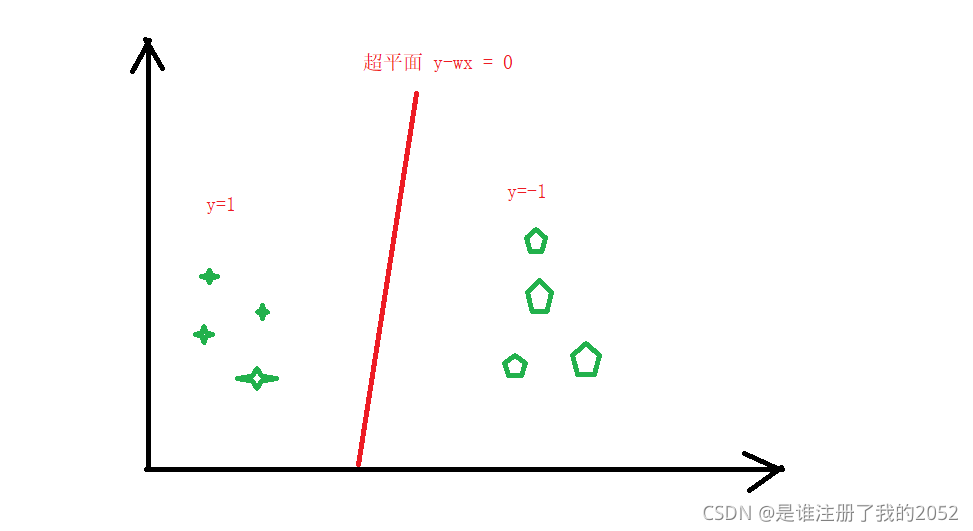
• wx>0 , y=1
• wx<0 , y=-1
• 综合以上得出 y*wx>0

如图:

$$\begin{gathered} SVM模型公式:满足以下两点 \\ s.t前提y\times (wx)>0 \\ max[marg(W,X)] \end{gathered}$$

三:SVM三个过程:间隔(建模),对偶(求解),核函数(升核)

3.1 间隔(建模)

第一步:距离公式和前提约束

$$\begin{gathered} 距离公式:max\frac{|W^{T}X+b|}{||W||} \\ 约束:s.t:y_i(W^T{x}_i+b)>0 \end{gathered}$$

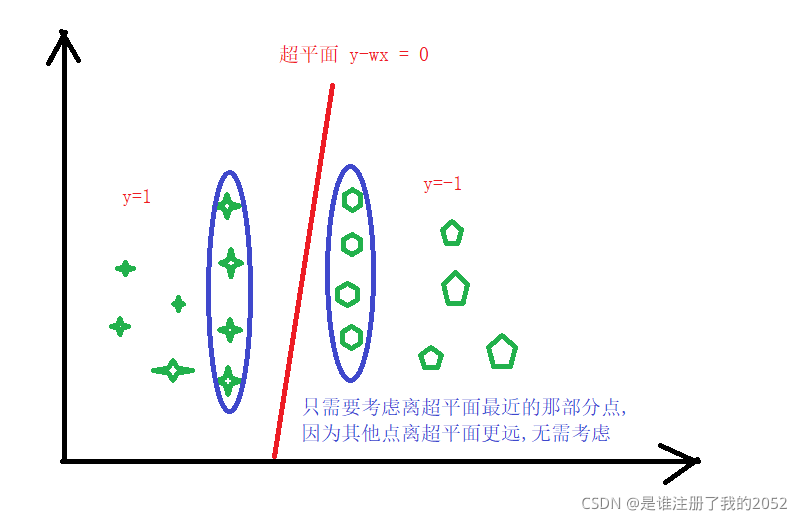
第二步:只需要考虑离超平面最近的点与超平面的距离即可

$$\begin{gathered} 只考虑离超平面最近的点:max(min\frac{|W^{T}X+b|}{||W||}) \\ 约束:s.t:y_i(W^T{x}_i+b)>0,假设存在\alpha >0,则y_i(W^T{x}_i+b)=\alpha >0 \\ 所以s.t:min(y_i(W^T{x}_i+b))=\alpha >0 \\ 因为:y\in [-1,1] \\ 所以:s.t:min|W^T{x}_i+b|=\alpha \end{gathered}$$

第三步:简化距离公式

$$\begin{gathered} max\frac{\alpha }{||W||} \\ s.t:min(y_i(W^T{x}_i+b))=\alpha \end{gathered}$$

第四步:缩放α

$$\begin{gathered} 缩放\alpha ,令\alpha =1,则公式简化为: \\ max\frac{1}{||W||} \\ s.t:min(y_i(W^T{x}_i+b))=1 \end{gathered}$$

第五步:根据二范式 ||W|| ,即W的平方再简化

$$\begin{gathered} max\frac{1}{||W||}=min||W||=min{W}^{T}W \\ s.t:min(y_i(W^T{x}_i+b))=1即y_i(W^T{x}_i+b)>=1 \\ 这一步结论: \\ min{W}^{T}W \\ s.t:y_i(W^T{x}_i+b)>=1 \end{gathered}$$

第六步:数学上称为QP问题

$$\begin{gathered} 凸优化:min{W}^{T}W \\ N个约束,因为x_i\in [1,N],s.t:y_i(W^T{x}_i+b)>=1 \end{gathered}$$

3.2 对偶(求解)

推导过程:有约束->无约束->对偶,上面结论是有约束

3.2.1 无约束推导过程:

$$\begin{gathered} 求解: \\ min{W}^{T}W\ast \frac{1}{2} \\ s.t:1-y_i(W^T{x}_i+b)<=0 \\ 转化成拉格朗日函数:拉格朗日函数的约束s.t:{\lambda }_i>0,表达式L(w,b,\lambda ),求max(L(w,b,\lambda )) \\ L(w,b,\lambda )=\frac{1}{2}{W}^{T}W+\sum _{i=1}^N{\lambda }_i(1-y_i(W^T{x}_i+b)) \\ s.t:{\lambda }_i>0 \\ 因为拉格朗日求max(L(w,b,\lambda )),同时拉格朗日中的1-y_i(W^T{x}_i+b)不再限制范围,则可以假设 \\ 假设1:1-y_i(W^T{x}_i+b)>0,则max(L(w,b,\lambda ))趋近于+\infty \\ 假设2:1-y_i(W^T{x}_i+b)<0,则max(L(w,b,\lambda ))趋近于\frac{1}{2}{W}^{T}W \\ 所以:最终结合SVM和拉格朗日公式表达式=min(max((L(w,b,\lambda ))),这个min是来自于距离公式 \\ SVM模型等价于min(max((L(w,b,\lambda ))) \\ 再根据拉格朗日公式的取值范围(+\infty ,\frac{1}{2}{W}^{T}W) \\ 所以:min(max((L(w,b,\lambda )))=min(+\infty ,\frac{1}{2}{W}^{T}W)=min(\frac{1}{2}{W}^{T}W) \\ 最终求解的是无约束的函数:min(\frac{1}{2}{W}^{T}W) \end{gathered}$$

3.3.2 对偶求解过程

第一步:对偶

因为对偶,所以符从下面转换
$$\frac{min}{W}\frac{max}{\lambda }L(W,\lambda ,b)=\frac{max}{\lambda }\frac{min}{W}L(W,\lambda ,b)$$

第二步:求导

$$\begin{gathered} L(W,\lambda ,b)=\frac{1}{2}{W}^{T}W+\sum _{i=1}^N{\lambda }_i(1-y_i(W^T{x}_i+b)) \\ 求极值,就是当导数=0的情况下,所以需要对函数进行求导 \\ 1.对W求导,\frac{\partial L(W,\lambda ,b)}{\partial W}=W-\sum _{i=1}^N{\lambda }_i{y}_i{x}_i=0,所以W=\sum _{i=1}^N{\lambda }_i{y}_i{x}_i \\ 2.对b求导,\frac{\partial L(W,\lambda ,b)}{\partial b}=-\sum _{i=1}^N{\lambda }_i{y}_i=0,所以\sum _{i=1}^N{\lambda }_i{y}_i=0 \end{gathered}$$

第三步:把第二步的结果代入函数,使用特殊符号代替W,简化函数书写

$$\begin{gathered} 从第二步结果中,使用\Delta 代替W,简化书写 \\ 第二步结果:1.\Delta =W=\sum _{i=1}^N{\lambda }_i{y}_i{x}_i,2.\sum _{i=1}^N{\lambda }_i{y}_i=0 \\ 代入函数简化之后L=\frac{1}{2}{\Delta }^T\Delta +\sum _{i=1}^N{\lambda }_i-\sum _{i=1}^N{\lambda }_i{y}_i({\Delta }^T{x}_i+b) \\ =\frac{1}{2}{\Delta }^T\Delta +\sum _{i=1}^N{\lambda }_i-\sum _{i=1}^N{\lambda }_i{y}_i{\Delta }^T{x}_i-\sum _{i=1}^N{\lambda }_i{y}_{i}b \\ 因为\sum _{i=1}^N{\lambda }_i{y}_i=0,所以最终L=\frac{1}{2}{\Delta }^T\Delta +\sum _{i=1}^N{\lambda }_i-\sum _{i=1}^N{\lambda }_i{y}_i{\Delta }^T{x}_i \end{gathered}$$

第四步:由于第三步简化之后,是需要条件的,所以最终结果是带约束的函数

$$\begin{gathered} \frac{max}{\lambda }L(\lambda )=\frac{1}{2}{\Delta }^T\Delta +\sum _{i=1}^N{\lambda }_i-\sum _{i=1}^N{\lambda }_i{y}_i{\Delta }^T{x}_i \\ s.t:{\lambda }_i\ge 0,\sum _{i=1}^N{\lambda }_i{y}_i=0 \end{gathered}$$

现在函数 L(λ) 就是关于 λ 的函数,可以通过拉格朗日 / 梯度下降的范式求解得到 λ 的值

然后通过 λ 的值再反推 W 的值,

第五步:通过KKT条件求解 b 的值

$$KKT条件\{\begin{array}{l}\frac{\partial L(\lambda )}{\partial \lambda }\\ 1-y_i(W^T{x}_i+b)\le 0\\ {\lambda }_i\ge 0\\ {\lambda }_i(1-y_i(W^T{x}_i+b))=0,这个公式是KKT条件的最重要的\end{array}$$

通过KKT条件进行求解b:
$$\begin{gathered} 因为:{\lambda }_i(1-y_i(W^T{x}_i+b))=0成立,所以 \\ 1.当{\lambda }_i=0时,1-y_i(W^T{x}_i+b)可以不等于0,这部分数据代表非最接近超平面的点 \\ 2.当{\lambda }_i\ne 0时,1-y_i(W^T{x}_i+b)=0,这部分数据代表距离超平面最近的点,看下图解释 \end{gathered}$$

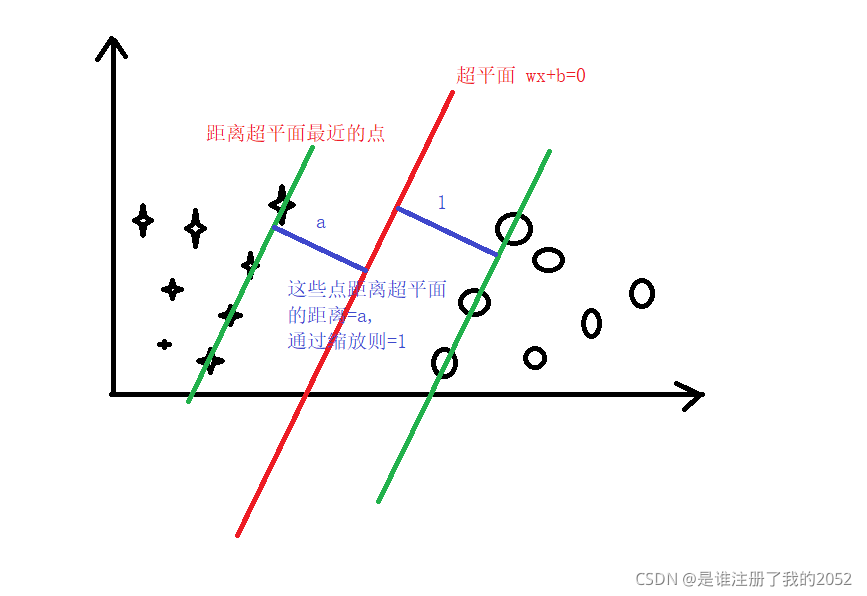
解释一下哪些是离超平面最接近的点:

由于缩放的结果,可以使用离超平面最近的点的数据可以求得 b 的值:
$$1-y_i(W^T{x}_i+b)=0,把离超平面最近的点(x_i,y_i)代入公式,即可得到b的解$$