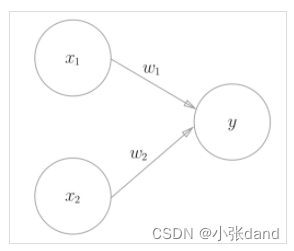
感知机是神经网络（深度学习）的起源的算法。感知机只对线性可分的数据有效。将感知机进行堆叠可以构造多层感知机。与感知机相比，多层感知机能够处理非线性可分的数据。下图展示了一个简单的感知机模型，其中x1,x2​是输入，w1,w2是权重，y=w1x1+w2x2是输出。

本实训项目的主要目标是学习和掌握多层感知机的原理，主要内容包括使用感知机实现与、或和与非逻辑门，以及使用多层感知机实现异或逻辑门。

第1关：使用感知机实现与、或、与非逻辑门

本关任务：
使用感知机实现与、或、与非逻辑门。
编程要求：
根据提示，在右侧编辑器中 Begin 和 End 之间补充代码，使用感知机实现与、或、与非逻辑门。

import numpy as np


def mlp_and(x1, x2):
    r'''
    使用感知机实现与逻辑门。

    参数：
    - x1: int (0 or 1)
    - x2: int (0 or 1)

    输出：
    - y: int (0 or 1)
        y = x1 and x2
    '''
    ########## Begin ##########
    w1,w2,theta = 0.5,0.5,0.7
    tmp = x1*w1 + x2*w2
    if tmp<=theta:
        return 0
    elif tmp > theta:
        return 1
    ########## End ##########


def mlp_or(x1, x2):
    r'''
    使用感知机实现或逻辑门。

    参数：
    - x1: int (0 or 1)
    - x2: int (0 or 1)

    输出：
    - y: int (0 or 1)
        y = x1 or x2
    '''
    ########## Begin ##########
    w1,w2,theta = 0.5,0.5,0.2
    tmp = x1*w1 + x2*w2
    if tmp<=theta:
        return 0
    elif tmp > theta:
        return 1
    ########## End ##########


def mlp_nand(x1, x2):
    r'''
    使用感知机实现与非逻辑门。

    参数：
    - x1: int (0 or 1)
    - x2: int (0 or 1)

    输出：
    - y: int (0 or 1)
        y = x1 nand x2
    '''
    ########## Begin ##########
    w1,w2,theta = -0.5,-0.5,-0.7
    tmp = x1*w1 + x2*w2
    if tmp<=theta:
        return 0
    elif tmp > theta:
        return 1
    ########## End ##########

第2关：使用多层感知机实现异或逻辑门

本关任务：
使用多层感知机实现异或逻辑门。
编程要求：
根据提示，在右侧编辑器中 Begin 和 End 之间补充代码，使用感知机实现异或逻辑门。实训已经提供了一组mlp_and、mlp_or和mlp_nand的实现，你需要利用它们实现mlp_xor。

import numpy as np


def mlp_and(x1, x2):
    x = np.array([x1, x2]).astype(np.float32)
    weight = np.array([0.5, 0.5]).astype(np.float32)
    bias = -0.7
    y = np.dot(weight, x) + bias
    if y <= 0:
        return 0
    else:
        return 1


def mlp_or(x1, x2):
    x = np.array([x1, x2]).astype(np.float32)
    weight = np.array([0.5, 0.5]).astype(np.float32)
    bias = -0.2
    y = np.dot(weight, x) + bias
    if y <= 0:
        return 0
    else:
        return 1


def mlp_nand(x1, x2):
    x = np.array([x1, x2]).astype(np.float32)
    weight = np.array([-0.5, -0.5]).astype(np.float32)
    bias = 0.7
    y = np.dot(weight, x) + bias
    if y <= 0:
        return 0
    else:
        return 1


def mlp_xor(x1, x2):
    r'''
    使用多层感知机实现异或逻辑门。

    参数：
    - x1: int (0 or 1)
    - x2: int (0 or 1)

    输出：
    - y: int (0 or 1)
        y = x1 xor x2
    '''
    ########## Begin ##########
    s1 = mlp_nand(x1, x2)
    s2 = mlp_or(x1, x2)
    y = mlp_and(s1, s2)
    return y
    ########## End ##########