写在前面:本博客仅作记录学习之用,部分图片来自网络,如需使用请注明出处,同时如有侵犯您的权益,请联系删除!
前言
在深度学习领域,网络架构的创新和性能的提升一直是研究的热点。在传统的神经网络设计中,激活函数扮演着至关重要的角色,它们为网络引入了非线性,使得网络能够学习和表示复杂的模式和结构。
近年来,逐元素乘积作为一种简单的操作,在各类神经网络中展现出惊人的潜力。它不仅能够有效融合不同来源的信息。在博客【CVPR_2024】:逐元素乘积为什么会产生如此令人满意的结果? 揭示了逐元素乘积具有将特征投射到极高维隐式特征空间的能力,为设计紧凑和高效网络提供了思路。简言之,网络缺少激活函数,也可基于逐元素乘积为网络提供非线性。
为了验证逐元素乘积在神经网络中的性能,本文以眼底视网膜血管分割任务为例进行了实验。视网膜血管分割是医学图像处理中的一个重要任务,它对于眼科疾病的诊断和治疗具有重要意义。本文选择U-Net作为基础网络架构,并在其中引入逐元素乘积操作,以验证其在缺少激活函数时的网络性能。
网络结构
编码结构
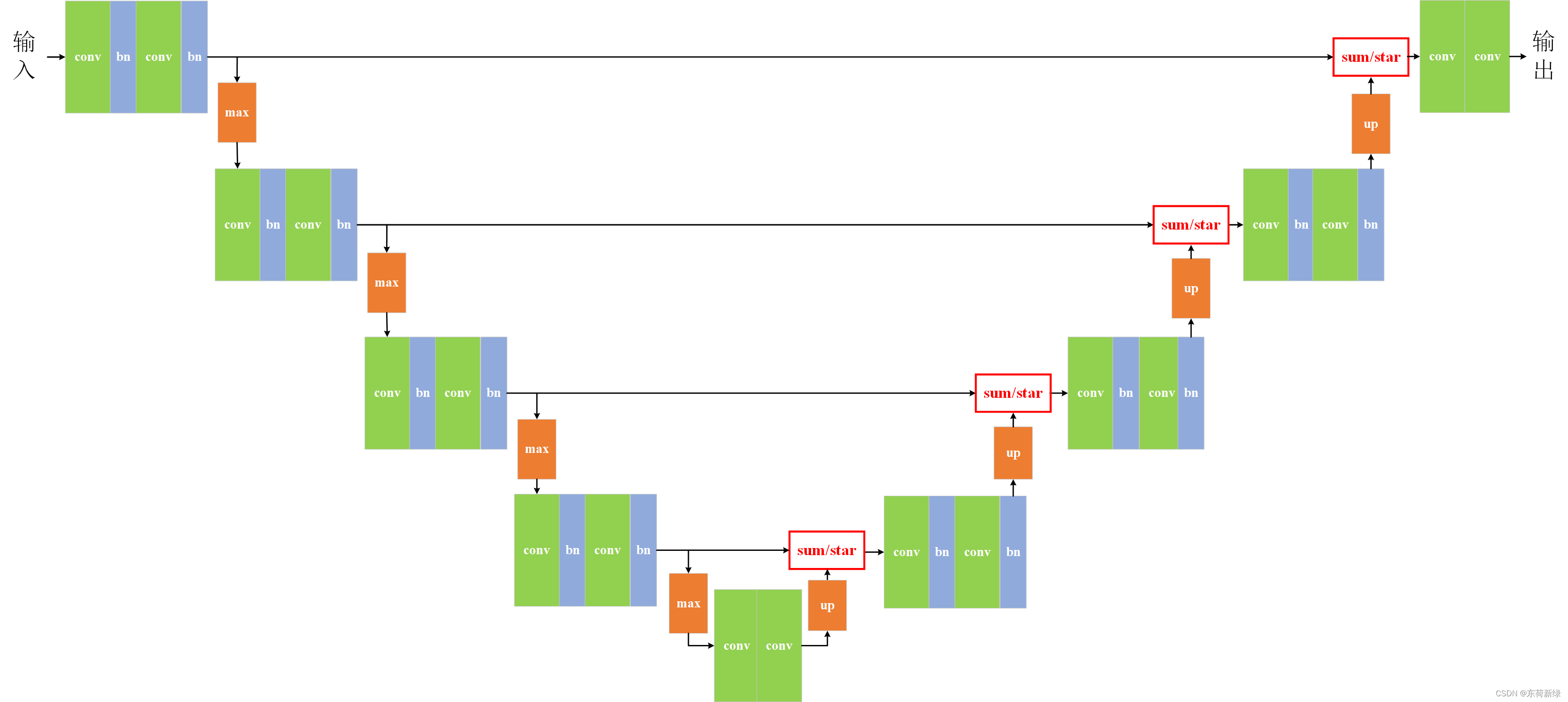
U-Net的编码结构(Encoder)是一种专为图像分割任务设计的深度卷积神经网络的重要组成部分。U-Net的编码结构采用了一种典型的卷积神经网络(CNN)架构,其主要目的是从输入图像中提取有用的特征信息。该结构通常由多个重复的卷积块组成,每个卷积块包含卷积层、BN、激活函数和池化层。
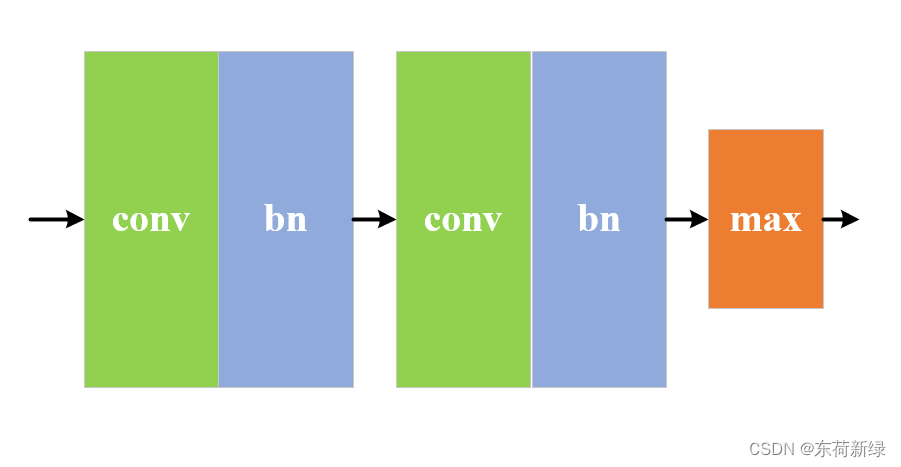
区别于传统的unet,本文去除了编码阶段所有激活函数,即编码部分只包含卷积、BN和池化层,结构如下图。具体组成:
卷积层:卷积核大小为3x3,步长(stride)为1,填充(padding)为1。
池化层:池化窗口的大小通常为2x2,步长为2。
解码结构
U-Net的解码结构是U-Net网络中的关键部分,主要用于从编码器提取的特征中恢复图像的空间分辨率和细节。解码器通过上采样操作逐步恢复图像尺寸,并与编码器中的对应层通过跳跃连接进行特征融合,以恢复丢失的空间信息。
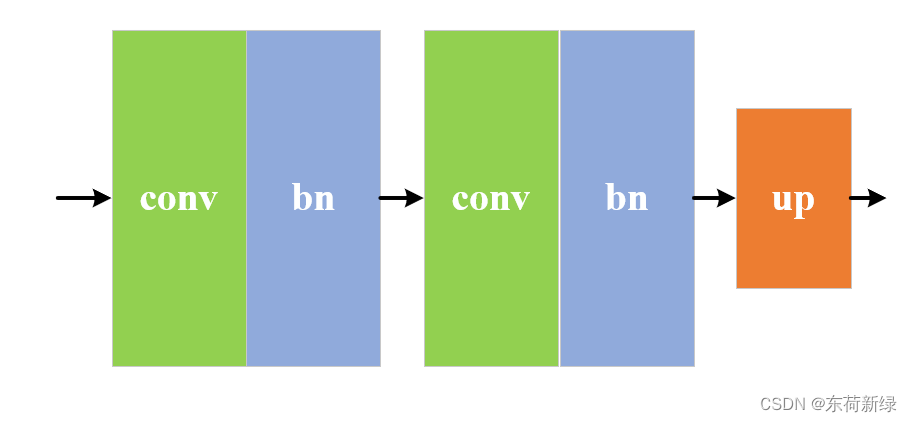
区别于传统的unet,本文去除了解码阶段所有激活函数,即解码部分只包含卷积、BN和上采样层,结构如下图。具体组成:
上采样层:最邻近插值法。
卷积层:卷积核大小为3x3,步长(stride)为1,填充(padding)为1。
代码
需要注意的是,本文为说明逐元素乘积的性能,将解码阶段中特征图拼接换为了sum/star,使得网络的参数进一步减少,网络更加紧凑。
同时,网络传入参数,设置了narrow,channel_multiplier参数用于控制网络通道以实现对网络参数的控制,return_feats参数则用于选择是否需要深度监督。
# ==============================U_Net—without ReLU====================================
class encode_block_wo_relu(nn.Module):
def __init__(self, ch_in, ch_out):
super(encode_block_wo_relu, self).__init__()
self.conv = nn.Sequential(
nn.Conv2d(ch_in, ch_out, kernel_size=3, stride=1, padding=1, bias=True),
NormLayer(ch_out, 'bn'),
nn.Conv2d(ch_out, ch_out, kernel_size=3, stride=1, padding=1, bias=True),
NormLayer(ch_out, 'bn'),
)
self.down = nn.MaxPool2d(kernel_size=2, stride=2)
def forward(self, x):
skip = self.conv(x)
x = self.down(skip)
return x, skip
class decode_block_wo_relu(nn.Module):
def __init__(self, ch_in, ch_out):
super(decode_block_wo_relu, self).__init__()
self.conv = nn.Sequential(
nn.Conv2d(ch_in, ch_out, kernel_size=3, stride=1, padding=1, bias=True),
NormLayer(ch_out, 'bn'),
nn.Conv2d(ch_out, ch_out, kernel_size=3, stride=1, padding=1, bias=True),
NormLayer(ch_out, 'bn'),
UpsampleLayer()
)
def forward(self, x):
x = self.conv(x)
return x
class U_Net_wo_relu(nn.Module):
def __init__(self, img_ch=3, output_ch=1, narrow=0.5, channel_multiplier=1, return_feats=False):
super(U_Net_wo_relu, self).__init__()
channels = {
'32': int(32 * channel_multiplier * narrow),
'64': int(64 * channel_multiplier * narrow),
'128': int(128 * channel_multiplier * narrow),
'256': int(256 * channel_multiplier * narrow),
'512': int(512 * channel_multiplier * narrow),
'1024': int(1024 * channel_multiplier * narrow),
'2048': int(2048 * channel_multiplier * narrow),
'4096': int(4096 * channel_multiplier * narrow),
}
self.return_feats = return_feats
self.up = UpsampleLayer()
self.encoder = nn.ModuleList()
self.decoder = nn.ModuleList()
self.encoder.append(encode_block_wo_relu(img_ch, channels['64']))
for i in range(0, 3):
self.encoder.append(
encode_block_wo_relu(channels[f'{64 * 2 ** i}'], channels[f'{64 * 2 ** (i + 1)}'])
)
self.decoder.append(decode_block_wo_relu(channels[f'512'], channels[F'512']))
for i in range(3, 0, -1):
self.decoder.append(
decode_block_wo_relu(channels[f'{int(64 * 2 ** i)}'], channels[f'{int(64 * 2 ** (i-1))}'])
)
self.out = nn.Conv2d(channels['64'], output_ch, kernel_size=1)
def forward(self, x):
skips = []
feats = []
# encode
for enc in self.encoder:
x, skip = enc(x)
skips.append(skip)
skips = skips[::-1]
# decode
for i, dec in enumerate(self.decoder):
x = dec(x)
# print(x.shape, skips[i].shape)
if i < len(self.decoder) - 1:
# x = x + skips[i]
x = x * skips[i]
if self.return_feats:
feats.append(x)
out = self.out(x)
pre = F.softmax(out, dim=1)
return pre, feats
实验
实验设置
实验的设置如下:
| 随机种子 | 验证集比例 | 批大小 | 早停 | 学习率 | 优化器 | 图像大小 | 数据集 |
|---|---|---|---|---|---|---|---|
| 2024 | 0.2 | 8 | 10 | 0.0005 | adam | 96x96 | STARE |
所有方法均在相同的设置下进行实验,保证实验的公平性,网络参数为2.94M,均选择在验证集上表现最优的权重进行测试。
w/o-ReLU的性能比较
下图给了sum和star两种方法的性能对比:
 sum-w/o-ReLU-ROC曲线 sum-w/o-ReLU-ROC曲线
|
 sum-w/o-ReLU-PR曲线 sum-w/o-ReLU-PR曲线
|
 star-w/o-ReLU-ROC曲线 star-w/o-ReLU-ROC曲线
|
 star-w/o-ReLU-PR曲线 star-w/o-ReLU-PR曲线
|
| 操作类型 | ROC | PR | F1 | Acc | SE | SP | pre |
|---|---|---|---|---|---|---|---|
| sum-w/o-ReLU | 0.9039 | 0.7139 | 0.6530 | 0.9271 | 0.5939 | 0.9706 | 0.7251 |
| star-w/o-ReLU | 0.9312 | 0.7407 | 0.6835 | 0.9330 | 0.6271 | 0.9729 | 0.7511 |
| 提升 | ↑ 2.73 % \textcolor{red}{\uparrow 2.73\%} ↑2.73% | ↑ 2.68 % \textcolor{red}{\uparrow 2.68\%} ↑2.68% | ↑ 3.05 % \textcolor{red}{\uparrow 3.05\%} ↑3.05% | ↑ 0.59 % \textcolor{red}{\uparrow 0.59\%} ↑0.59% | ↑ 3.32 % \textcolor{red}{\uparrow 3.32\%} ↑3.32% | ↑ 0.23 % \textcolor{red}{\uparrow 0.23\%} ↑0.23% | ↑ 2.60 % \textcolor{red}{\uparrow 2.60\%} ↑2.60% |
 sum-w/o-ReLU sum-w/o-ReLU
|
 star-w/o-ReLU star-w/o-ReLU
|
如上所示,star操作在各个指标上均取得了更佳的性能,分别获得了0.2%到3%不等的提升,从定性的图像中来看,网络似乎对较大的血管具有更好的分割效果,同时血管分割的结果也更加光滑。
with-ReLU的性能比较
下图给了sum和star两种方法的性能对比:
 sum-with-ReLU-ROC曲线 sum-with-ReLU-ROC曲线
|
 sum-with-ReLU-PR曲线 sum-with-ReLU-PR曲线
|
 star-with-ReLU-ROC曲线 star-with-ReLU-ROC曲线
|
 star-with-ReLU-PR曲线 star-with-ReLU-PR曲线
|
| 操作类型 | ROC | PR | F1 | Acc | SE | SP | pre |
|---|---|---|---|---|---|---|---|
| sum-with-ReLU | 0.9743 | 0.8732 | 0.7846 | 0.9500 | 0.7888 | 0.9710 | 0.7805 |
| star-with-ReLU | 0.9706 | 0.8613 | 0.7750 | 0.9483 | 0.7715 | 0.9713 | 0.7786 |
| 提升 | ↓ 0.37 % \textcolor{blue}{\downarrow 0.37\%} ↓0.37% | ↓ 1.19 % \textcolor{blue}{\downarrow 1.19\%} ↓1.19% | ↓ 0.96 % \textcolor{blue}{\downarrow 0.96\%} ↓0.96% | ↓ 0.17 % \textcolor{blue}{\downarrow 0.17\%} ↓0.17% | ↓ 1.73 % \textcolor{blue}{\downarrow 1.73\%} ↓1.73% | ↑ 0.03 % \textcolor{red}{\uparrow 0.03\%} ↑0.03% | ↓ 0.19 % \textcolor{blue}{\downarrow 0.19\%} ↓0.19% |
 sum-with-ReLU sum-with-ReLU
|
 star-with-ReLU star-with-ReLU
|
如上所示,star操作在各个指标上均有不同程度的下降,总体来说,两者的性能差不多,从定性的图像中来看,star操作对血管连续上有较差的表现。
总结
本文将U-Net解码中的特征拼接修改为逐元素求和和逐元素乘积,并针对血管分割任务进行了性能评估。实验结果显示,在无激活函数时,逐元素乘积在多个关键指标上均优于逐元素求和,性能提升幅度在0.2%至3%之间,表明逐元素乘积确实能在一定程度上提供更高维度的隐式空间。从分割结果来看,逐元素乘积似乎对较大的血管具有更好的分割效果,能够更准确地捕捉血管的轮廓和细节。同时,star网络的分割结果也表现出更高的光滑性和一致性,减少了噪声和伪影的干扰,从而提高了分割结果的可靠性和可读性。在使用激活函数时,逐元素乘积在多个关键指标上均低于于逐元素求和,表明逐元素乘积的优势会倍激活函数所湮没。总言之,网络中要摒弃激活函数还有很长的路要走。
致谢
欲尽善本文,因所视短浅,怎奈所书皆是瞽言蒭议。行文至此,诚向予助与余者致以谢意。