前面已经学习了基本的3D作图,具体链接如下:
直方图教程:python画图|3D直方图基础教程-CSDN博客
垂线标记教程:python画图|3D垂线标记-CSDN博客
3D surface教程:python画图|3D surface基础教程-CSDN博客
在此基础上,今天尝试学习参数化图形输出教程。
【1】官网教程
首先依然是进入官网学习:
https://matplotlib.org/stable/gallery/mplot3d/lines3d.html
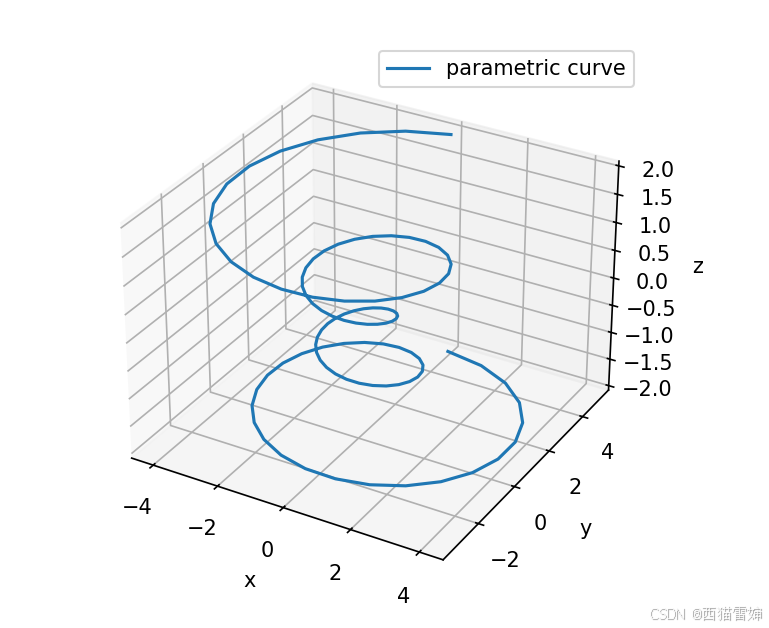
官网示例给出了漂亮的参数化曲线结果,下述为对官网代码的解读。
【2】代码解读
首先引入numpy和matplotlib。
import matplotlib.pyplot as plt #引入matplotlib模块画图 import numpy as np #引入numpy模块做数学计算
然后快速定义了要画3D图:
ax = plt.figure().add_subplot(projection='3d') #定义画图,指明为3D图
画图应当有数据,因此定义了参数和各个变量:
theta = np.linspace(-4 * np.pi, 4 * np.pi, 100) #定义参数变量theta z = np.linspace(-2, 2, 100) #定义参数变量z r = z**2 + 1 #定义因变量r x = r * np.sin(theta) #定义自变量x y = r * np.cos(theta) #定义自变量y
上述代码中,theta为最初的参数;但这里同样把Z也取成了参数。
然后,定义了按照x、y和z的方式输出图形:
ax.plot(x, y, z, label='parametric curve') #定义输出图形
最后对图形属性做了规定:
ax.plot(x, y, z, label='parametric curve') #定义输出图形 ax.legend() #定义输出标签 plt.show() #输出图形
完整的代码注解和输出图形为:
import matplotlib.pyplot as plt #引入matplotlib模块画图
import numpy as np #引入numpy模块做数学计算
ax = plt.figure().add_subplot(projection='3d') #定义画图,指明为3D图
# Prepare arrays x, y, z
theta = np.linspace(-4 * np.pi, 4 * np.pi, 100) #定义参数变量theta
z = np.linspace(-2, 2, 100) #定义参数变量z
r = z**2 + 1 #定义因变量r
x = r * np.sin(theta) #定义自变量x
y = r * np.cos(theta) #定义自变量y
ax.plot(x, y, z, label='parametric curve') #定义输出图形
ax.legend() #定义输出标签
plt.show() #输出图形图1
【3】代码修改
在代码修改前,我们先在plt.show()前加一行代码用以输出轴标签:
ax.set(xlabel='x',ylabel='y',zlabel='z') #要求输出坐标轴标签
【3.1】交换r和Z
官网教程将Z定义为参数,现在尝试交换r和Z,Z作为因变量,改后代码为:
# Prepare arrays x, y, z
theta = np.linspace(-4 * np.pi, 4 * np.pi, 100) #定义参数变量theta
r = np.linspace(-2, 2, 100) #定义参数变量r
z = r**2 + 1 #定义因变量z
x = z * np.sin(theta) #定义自变量x
y = z * np.cos(theta) #定义自变量y
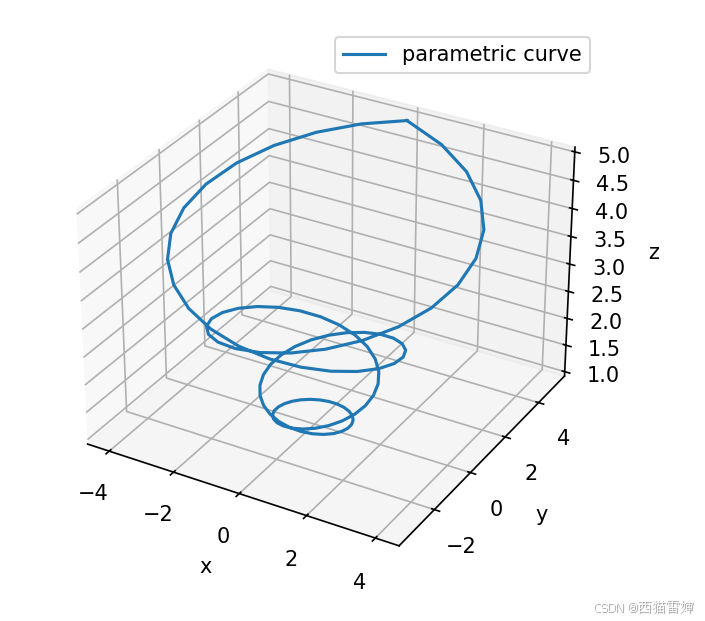
此时的输出结果为:
图2
可见,新的代码下输出图像已经完全不同。
【3.2】交换x和z
官网教程将plot输出图形时按照xyz的顺序,现在尝试携程zyx的顺序,改后代码为:
ax.plot(z, y, x, label='parametric curve') #定义输出图形
输出结果为:
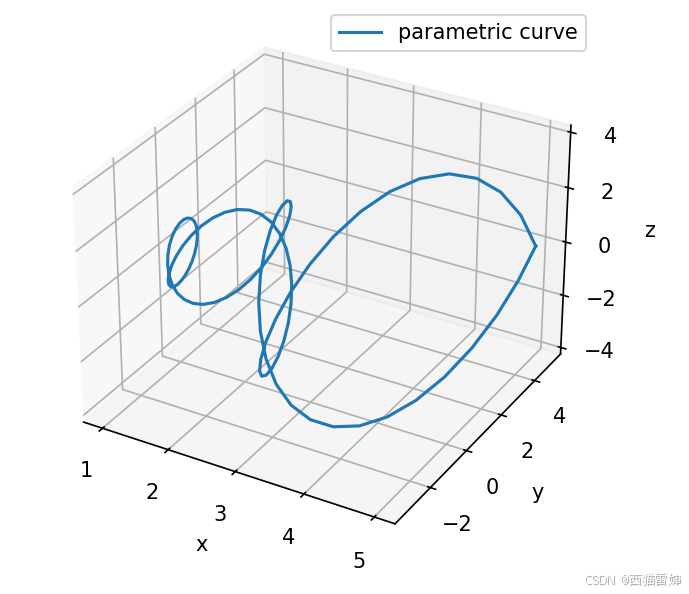
图3
由图3和图2对比可见,图形“底座”从xoy平面旋转到了yoz平面。
至此的完整代码为:
import matplotlib.pyplot as plt #引入matplotlib模块画图
import numpy as np #引入numpy模块做数学计算
ax = plt.figure().add_subplot(projection='3d') #定义画图,指明为3D图
# Prepare arrays x, y, z
theta = np.linspace(-4 * np.pi, 4 * np.pi, 100) #定义参数变量theta
r = np.linspace(-2, 2, 100) #定义参数变量r
z = r**2 + 1 #定义因变量z
x = z * np.sin(theta) #定义自变量x
y = z * np.cos(theta) #定义自变量y
ax.plot(z, y, x, label='parametric curve') #定义输出图形
ax.legend() #定义输出标签
ax.set(xlabel='x',ylabel='y',zlabel='z') #要求输出坐标轴标签
plt.show() #输出图形【4】改写代码
尝试完全修改参数和变量,依然按照xyz的顺序输出,改后代码为:
theta = np.linspace(-4 * np.pi, 4 * np.pi, 100) #定义参数变量theta x = theta #定义自变量x y =np.cos(theta) #定义自变量y z =np.sin(theta) #定义自变量z ax.plot(x, y, z, label='parametric curve') #定义输出图形
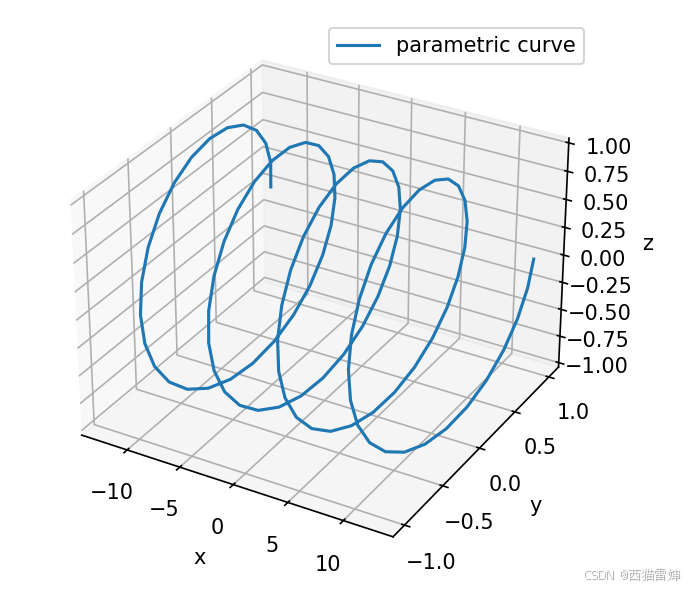
输出图形为:
图4
图4展示了新的输出图形。
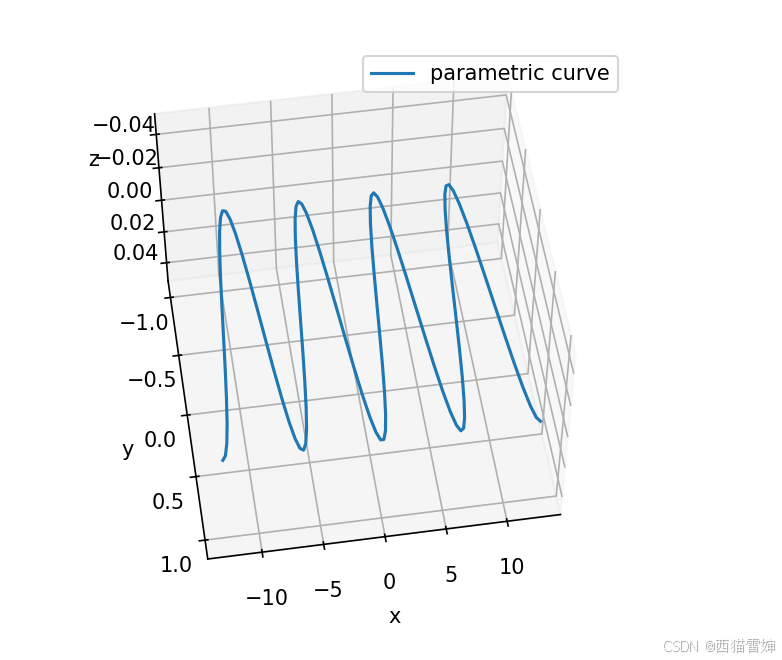
未做对比,继续修改代码,设定z=0:
z =0 #定义自变量z
输出结果为:
图5
可见,在xoy,输出了 y =np.cos(x)的正弦函数图像。
【5】总结
学习了3D参数化图形输出,尝试修改了参数和函数,均获得了期待的3D图形。