蓝桥杯算法合集: 蓝桥杯算法合集(终极完结版)
回溯法
思想
回溯法是一种择优搜索法。也叫试探法,按择优条件向前搜索,以达到目标。当探索到某一步时,发现原来现则并不优或者被强行return,就退回一步重新选择。这种走不通就退回再走的方法就称作回溯法。通常于递归搭配在一起使用。
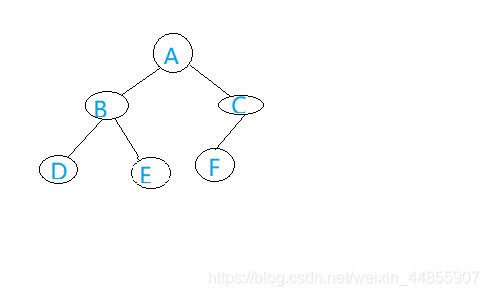
例如
例如
当从B到走到D这状态不满足目标时,就退回一步回溯到B走下一个没有尝试的状态E(通常是外层循环来驱动的),这一过程就叫回溯。
应用
树、图的深度优先搜索
可以使用位运算压缩空间。如解决N皇后问题时,使用Byte和short类型存储列和斜线的状态.
位运算知识:
1. 基本类型的位数
一个字节等于8位 1byte = 8bit。
char占用的是2个字节 16位,所以一个char类型的可以存储一个汉字。
整型:
byte:1个字节 8位
short :2个字节 16位
int :4个字节 32位
long:8个字节 64位
浮点型:
float:4个字节 32 位
double :8个字节 64位
注:默认的是double类型,如3.14是double类型的,加后缀F(3.14F)则为float类型的。
char类型:
char:2个字节。
Boolean 类型
boolean: (true or false)(并未指明是多少字节 1字节 1位 4字节)
2.基本类型的存储范围 最大值和最小值。
-
short(10^5)
最小值:Short.MIN_VALUE=-32768 (-2的15次方)
最大值:Short.MAX_VALUE=32767 (2的15次方-1) -
int(10^10)
最小值:Integer.MIN_VALUE= -2147483648 (-2的31次方)
最大值:Integer.MAX_VALUE= 2147483647 (2的31次方-1) -
long(10^19)
最小值:Long.MIN_VALUE=-9223372036854775808 (-2的63次方)
最大值:Long.MAX_VALUE=9223372036854775807 (2的63次方-1) -
float(10^38)
最小值:Float.MIN_VALUE=1.4E-45 (2的-149次方)
最大值:Float.MAX_VALUE=3.4028235E38 (2的128次方-1)
5.double(10^30)
最小值:Double.MIN_VALUE=4.9E-324 (2的-1074次方)
最大值:Double.MAX_VALUE=1.7976931348623157E30
位运算
*想知道A某一位是1还是0 只需和该位为1其他位为0的数按位与即可
将A某一位 置为1 只需和该位为1其他位为0的数按位或
将A某一位 置为0 只需和该位为0其他位为1的数按位与
a跟1与 a以前是什么现在还是什么
a跟0或 a以前是什么现在还是什么
部分代码如下
for(int i=0;i<8;i++) {
//row行的i列尝试放置皇后
queens[row]=i;
//判断该列 对角线是否为1 按位与1作与运算
//如要知道第二列要没有放置皇后
//cols:01100001
//cv:& 00000100
//cols&cv 0
int cv= 1<<i;
if(( cols & cv )!=0 ) continue ;
int lv=1<< (row-i+7);
if((leftTop & lv)!=0 )continue ;
int rv=1<< (row+i);
if((rightTop & rv)!=0) continue;
//将该列 对角线置为1
//如将第二列置为皇后
//cols:01100001
//cv: 00000100
//cols|cv 1
cols |=cv;
leftTop |=lv;
rightTop |=rv;
place(row+1);
//将该列 对角线重置为0 ~表示取反
//cols:01100101
//cv: 00000100
//~cv: 11111011
//~cv&cols: 01100001
cols &= ~cv;
leftTop &= ~lv;
rightTop &= ~rv;
}
N皇后
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,
使得它们不相互攻击(即任意2个皇后不允许处在同一排,
同一列,也不允许处在与棋盘边框成45角的斜线上。
给定一个整数 n,返回 n 皇后不同的解决方案的数量。
解法一:暴力法
package 回溯;
public class N皇后_整型数组标记 {
int ways;
/*
* cols数组 索引为皇后行号 值为改行皇后放置的位置
*/
int[]cols;
void placeQueens(int n) {
//判掉不合法的
if(n<1) return;
cols=new int[n];
place(0);
System.out.println(ways);
}
/**
* 从第 row行尝试开始摆放皇后
*/
void place(int row) {
//递归出口
if(row==cols.length) {
ways++;
show();
return;
}
for(int col=0;col<cols.length;col++) {
if(isValid(row,col)) {//如果该行该列没有放置过皇后
//第row行的皇后放在col列
cols[row]=col;
//开始摆放下一行
place(row+1);
//回溯 由于是用整型数组标记某一行的皇后放在某一列
//故改值会被另一个列的摆法的覆盖 无需修改
}
}
}
public boolean isValid(int row, int col) {
for(int i=0;i<row;i++) {
//col列已经有皇后在上面了
if(cols[i]==col) return false;
//对角线 斜率为正负一 x1-x2=|y1-y2|
if(row-i==Math.abs(col-cols[i]))return false;
}
return true;
}
public void show() {
for(int i=0;i<cols.length;i++) {
for(int j=0;j<cols.length;j++) {
if(cols[i]==j) {
System.out.print("1 ");
}else {
System.out.print("0 ");
}
}
System.out.println();
}
System.out.println("-------------");
}
public static void main(String[] args) {
new N皇后_整型数组标记().placeQueens(4);
}
}
解法二:回溯+剪枝
package 回溯;
import java.util.Scanner;
public class N皇后_布尔数组 {
int ways;
/*cols数组标记某一列有没有放过皇后
* leftTop为自左上角到右下角的斜线 n行有2*n-1条
* rightTop为自右上角到左下角的斜线 n行有2*n-1条
*
*/
boolean[]cols;
boolean[]leftTop;
boolean[]rightTop;
void placeQueens(int n) {
if(n<1) return;
cols=new boolean[n];
leftTop=new boolean[n*2];
rightTop=new boolean[n*2];
place(0);
System.out.println(ways);
}
void place(int row) {
if(row==cols.length) {
ways++;
return;
}
for(int col=0;col<cols.length;col++) {
//可行性剪枝
if(cols[col])continue;
int ltIndex=row-col+cols.length-1;
if(leftTop[ltIndex])continue;
int rtIndex=row+col;
if(rightTop[rtIndex])continue;
//标记
cols[col]=leftTop[ltIndex]=rightTop[rtIndex]=true;
place(row+1);
//回溯
cols[col]=leftTop[ltIndex]=rightTop[rtIndex]=false;
}
}
public static void main(String[] args) {
Scanner reader=new Scanner(System.in);
new N皇后_布尔数组().placeQueens(4);
}
}
解法三:回溯+剪枝+位运算
package 回溯;
public class N皇后_位运算 {
/*用8位的Byte和16位的数据类型存放01状态表示棋盘的摆放状况
*
*/
int [] queens;
byte cols;
short leftTop;
short rightTop;
int ans;
void Equeens() {
queens=new int[8];
place(0);
}
void place(int row) {
System.out.println(row);
if(row==8) {
ans++;
return;
}
for(int i=0;i<8;i++) {
//row行的i列尝试放置皇后
queens[row]=i;
//判断该列 对角线是否为1 按位与1作与运算
//如要知道第二列要没有放置皇后
//cols:01100001
//cv:& 00000100
//cols&cv 0
int cv= 1<<i;
if(( cols & cv )!=0 ) continue ;
int lv=1<< (row-i+7);
if((leftTop & lv)!=0 )continue ;
int rv=1<< (row+i);
if((rightTop & rv)!=0) continue;
//将该列 对角线置为1
//如将第二列置为皇后
//cols:01100001
//cv: 00000100
//cols|cv 1
cols |=cv;
leftTop |=lv;
rightTop |=rv;
place(row+1);
//将该列 对角线重置为0 ~表示取反
//cols:01100101
//cv: 00000100
//~cv: 11111011
//~cv&cols: 01100001
cols &= ~cv;
leftTop &= ~lv;
rightTop &= ~rv;
}
}
public static void main(String[] args) {
new N皇后_位运算().Equeens();
}
}
对比解法一和二,可以看到使用布尔数组标记后,如果要求得所有解或者是最优解,回溯部分代码需要将标记取消。而使用整型数组则不用。
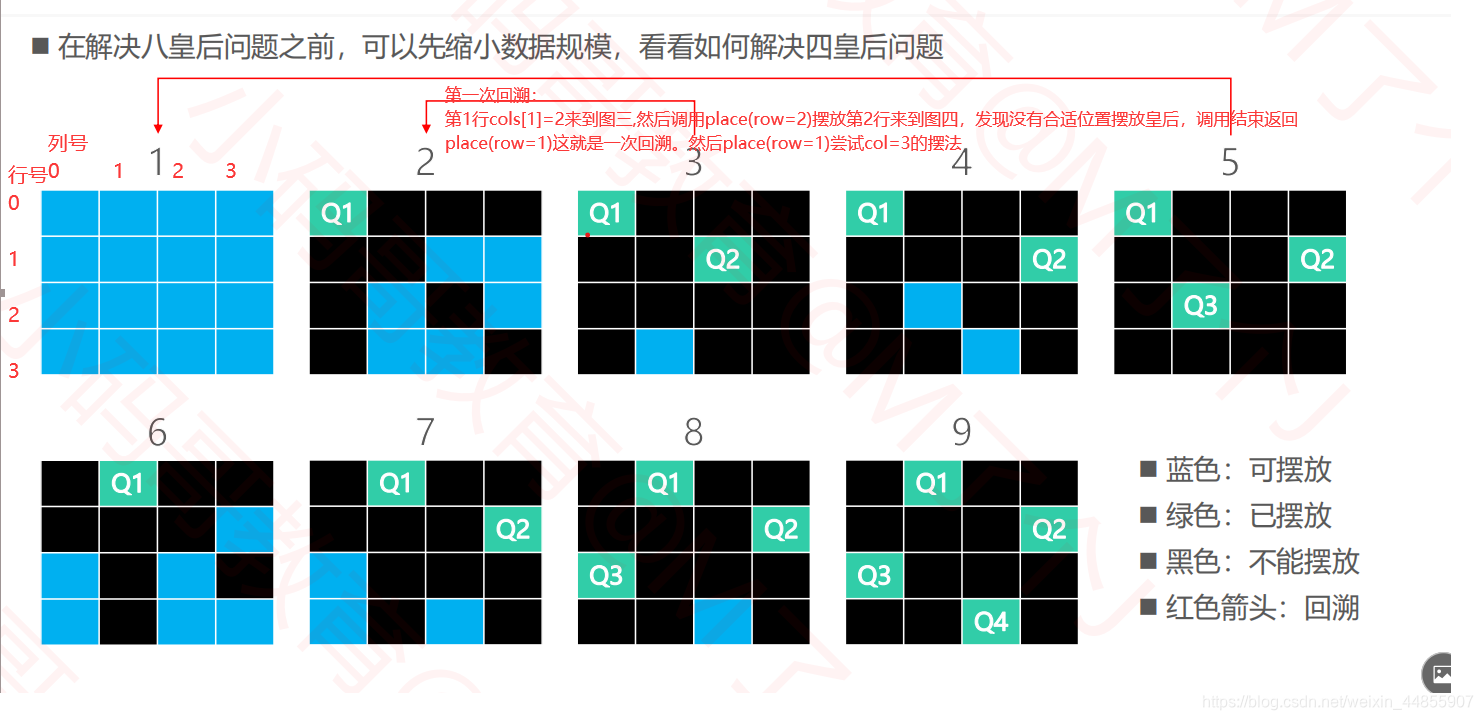
下面通过四皇后走法图例来进入一步了解回溯法