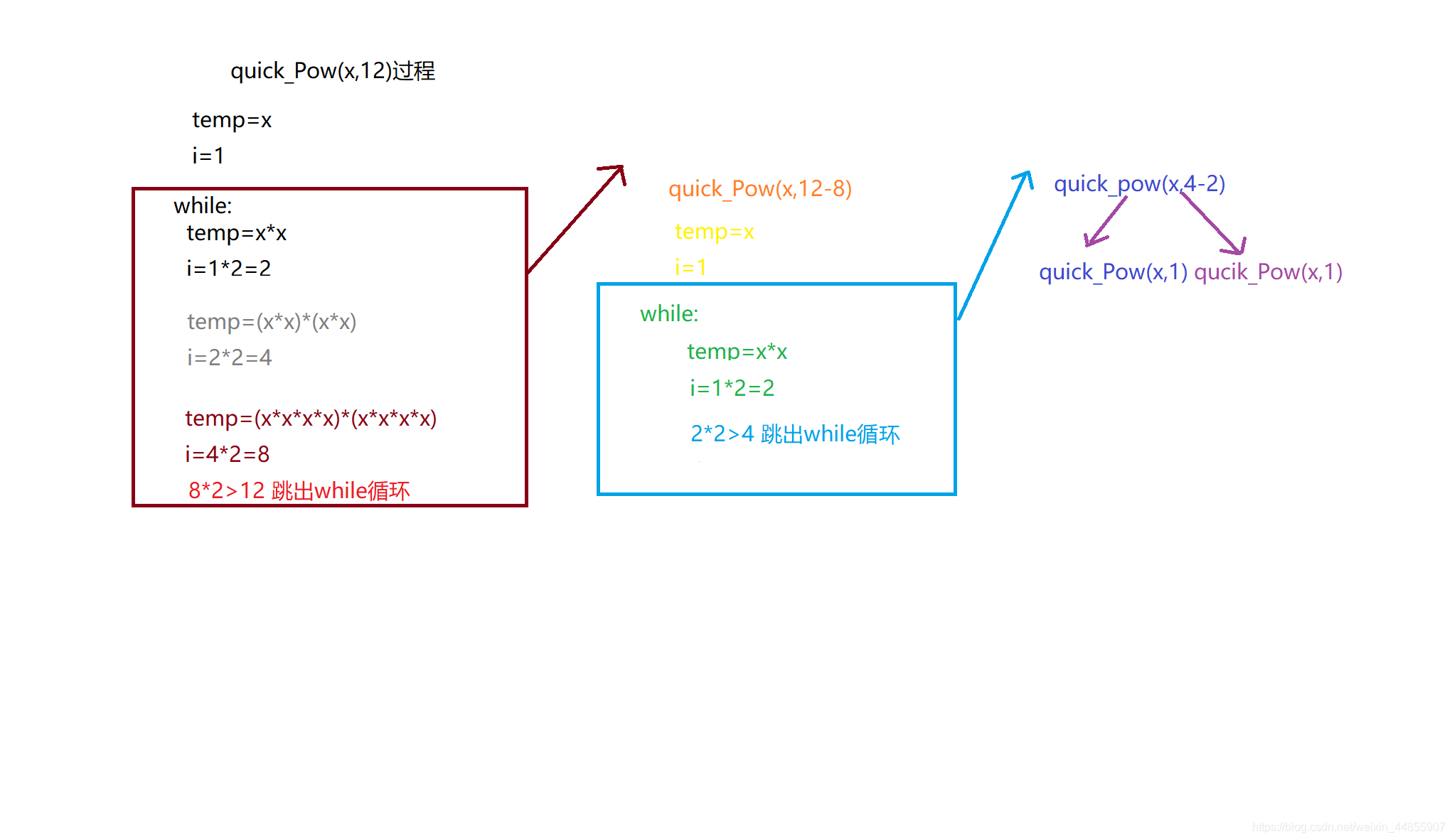
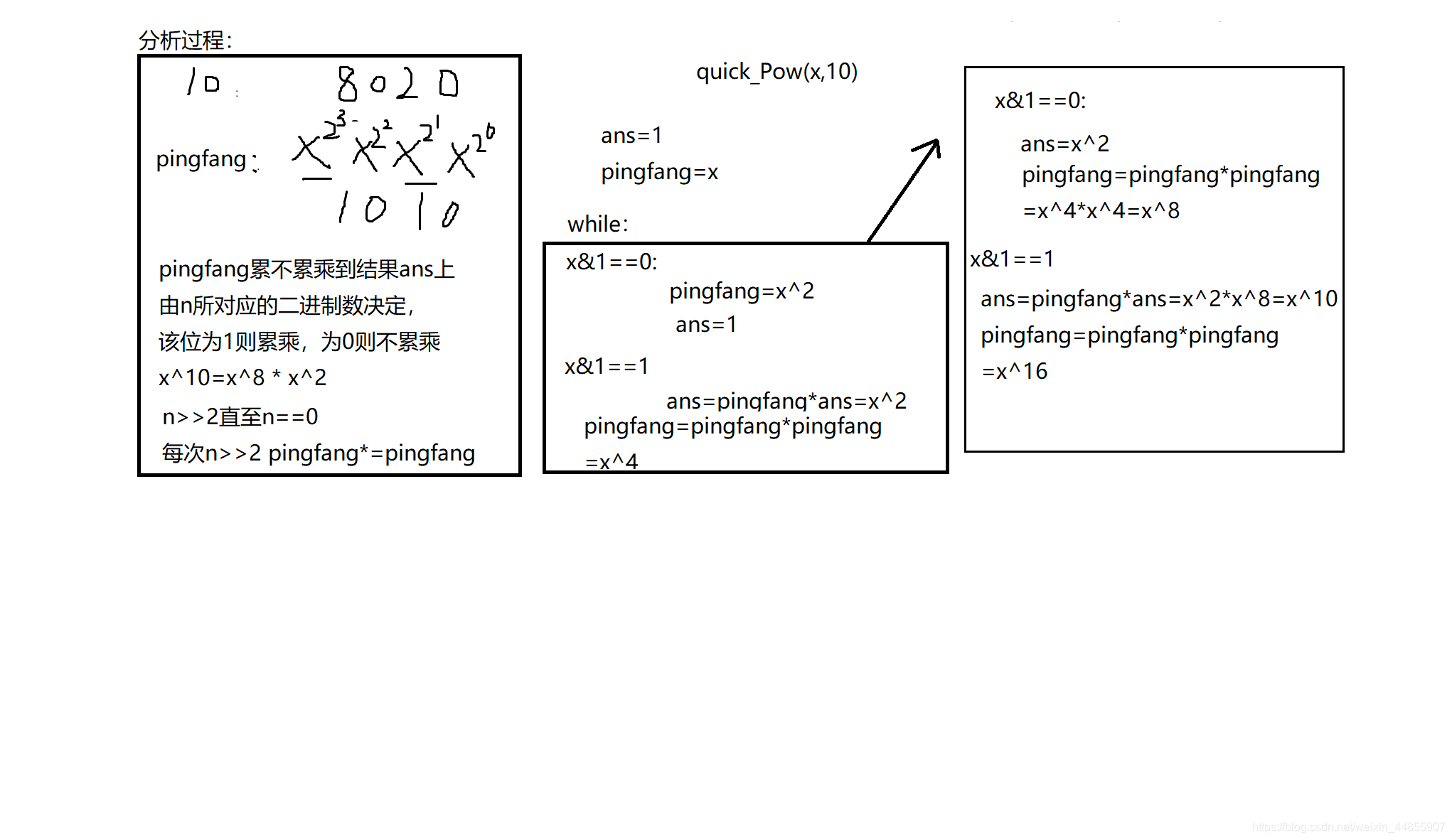
一、数字快速幂

求x的n次方

package 分治法;

public class 快速幂_初始版 {
	/*
	 * 以最快速度求x的n次方
	 * 时间复杂度：O(log n)
	 */
	public static long quick_Pow(long x,int n) {
		if(n==1)
			return x;
		long temp=x;//x的一次方
		int i=1;   //指数从1开始
		while((i<<1)<n) {
			temp*=temp;//乘方
			i=i<<1; //底数乘方 对应指数翻一倍
			System.out.println(temp+" "+i);
		}
		long ans=quick_Pow(x,n-i);
		ans=ans*temp;
		return ans;
	}

	public static void main(String[] args) {
		System.out.println(quick_Pow(6,12));

	}

}

分析见图片

package 分治法;

public class 快速幂_位运算 {
	static long quick_Pow(long x,int n) {
		if(n==0)
			return 1;
		if(n==1)
			return x;
		long ans=1;
		long pingfang=x; //x的一次方
		while(n!=0) {
			if( (n&1)==1 ) {
				ans*=pingfang;
			}
			pingfang*=pingfang;
			n>>=1; //
		}
		return ans;
	}

	public static void main(String[] args) {
		System.out.println(quick_Pow(2,10));

	}

}

二、矩阵快速幂

矩阵快速幂法解斐波那契数列

有一对兔子，从出生后第3个月起，每个月都生一对兔子，小兔子长到第三个月后每个月又生一对兔子。
假如兔子都不死，求第n个月兔子对数

package 数学类;

import java.util.Scanner;

public class 斐波那契数列_矩阵幂运算 {

	public static void main(String[] args) {
		Scanner reader=new Scanner(System.in);
		int n=reader.nextInt();
		if(n==1||n==2) {
			System.out.println(1);
			//结束程序
			System.exit(0);
		}
		//T矩阵 两行两列
		long[][] T= {
				{0,1},
				{1,1}};	
		//求矩阵T的n-1次方幂
		long[][] ans=matrixPow(T,n-1);
		
		//ans矩阵与[f_1,f_2]矩阵相乘 得到的矩阵的第一个元素就是f_n
		//ans   一行两列 *两行两列得到一行两列
		//不合法运算：matrixMutiply(ans,new long[][] {{1,1}})
		ans=matrixMutiply(new long[][] {{1,1}},ans);
		System.out.println(ans[0][0]);

	}
	//矩阵乘法
	private static long[][] matrixMutiply(long[][] a, long[][] b) {
		//新矩阵的行数和列数分别为a的行数 和b的列数
		final int m=a.length;
		final int n=b[0].length;
		final int q=a[0].length;
		//不满足矩阵乘法的运算
		if(q!=b.length)
			throw new IllegalArgumentException();
		long[][]  ret=new long[m][n];
		for(int i=0;i<m;i++) {
			for(int j=0;j<n;j++) {
				
				for(int k=0;k<q;k++) {
					ret[i][j]+=a[i][k]*b[k][j];
				}
			}
		}
		
		return ret;
	}
	//矩阵幂运算 一定是方阵
	private static long[][] matrixPow(long[][] x, int n) {
		long [][] ans=new long[ x.length ][ x[0].length ];
		//单位矩阵即 对角线为1其余皆为0的矩阵 相当于数字快速幂中的1
		for(int i=0;i<ans.length;i++)
			ans[i][i]=1;
		//平方数
		long pingFang[][]=x; //一次方
		
		while(n!=0) {
			if( (n&1)==1 ) {
				ans=matrixMutiply(ans,pingFang);
			}
			pingFang=matrixMutiply(pingFang, pingFang);
			n>>=1;
		}
		return ans;
	}

}