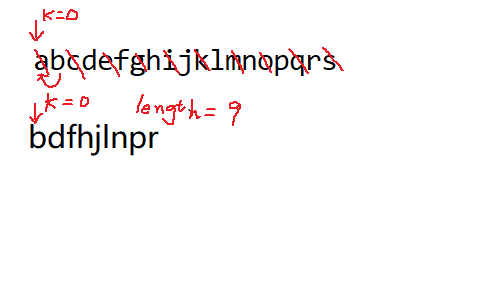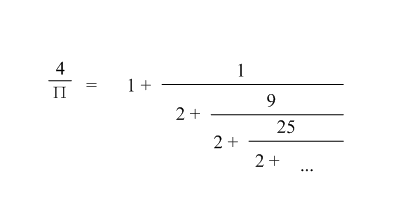Java实现蓝桥杯第五届2014年真题

蓝桥杯第五届真题

武功秘籍
切面条
猜字母
- 数组模拟
- 字符串保存
大衍数列
圆周率
奇怪的分式
扑克序列
分糖果
地宫取宝
矩阵翻硬币

我开始想象不出来，自己高三那会是怎么正午两三点钟还能精神抖擞地上课。一到夏天就不想动。整个五一就刷了一套题。

武功秘籍

【题目描述】

小明到X山洞探险，捡到一本有破损的武功秘籍（2000多页！当然是伪造的）。他注意到：书的第10页和第11页在同一张纸上，但第11页和第12页不在同一张纸上。

小明只想练习该书的第81页到第92页的武功，又不想带着整本书。请问他至少要撕下多少张纸带走？

这是个整数，请通过浏览器提交该数字，不要填写任何多余的内容。

切面条

【题目描述】

一根高筋拉面，中间切一刀，可以得到2根面条。

如果先对折1次，中间切一刀，可以得到3根面条。

如果连续对折2次，中间切一刀，可以得到5根面条。

那么，连续对折10次，中间切一刀，会得到多少面条呢？

答案是个整数，请通过浏览器提交答案。不要填写任何多余的内容。

打开win10自带的画图工具，画图。得到如下：

折数	面条根数
0	2
1	3
2	5
3	9

答案：
2^10 + 1 = 1025

猜字母

【题目描述】

把abcd...s共19个字母组成的序列重复拼接106次，得到长度为2014的串。

接下来删除第1个字母（即开头的字母a），以及第3个，第5个等所有奇数位置的字母。

得到的新串再进行删除奇数位置字母的动作。如此下去，最后只剩下一个字母，请写出该字母。

答案是一个小写字母，请通过浏览器提交答案。不要填写任何多余的内容。
答案：q

注意是删除所有的奇数位置字母

数组模拟

package 第五届;

public class t03_猜字母 {

	public static void main(String[] args) {

		String s = "abcdefghijklmnopqrs";
		String news="";
		for(int i=1;i<=106;i++) {
			news+=s;
		}
		char c[] = news.toCharArray();
		int n = c.length; //字符串初始长度
		
		while(n > 1) {
			//新字符串的起始位置
			int k = 0;
			//模拟删除：奇数下标位置覆盖偶数下标位置
			for(int i = 1; i < n; i +=2) {
				c[k ++ ] = c[i];
			}
			//一轮删除后 新字符串的长度
			n = k; 
		}
		System.out.println(c[0]);
	}

}

如图：

在这里插入图片描述

字符串保存

实际上最简单的方法每轮删除奇数位置时，使用一个字符串保留偶数位置字母。循环删除直至字符串长度为1.

public class t03_猜字母2 {

	public static void main(String[] args) {
		String s = "abcdefghijklmnopqrs";
		String news="";
		for(int i=1;i<=106;i++) {
			news+=s;
		}
		char c[] = news.toCharArray();
		int n = c.length; //字符串初始长度
		while( n > 1) {
			StringBuffer sb = new StringBuffer();
			for(int i = 0; i < n; i ++) {
				if( (i & 1) == 1)  //新字符串只保留偶数位置字符串
					sb.append(c[i]);
			}
			n = sb.length(); //删除奇数位置之后 新字符串的长度
			c = sb.toString().toCharArray();
		}
		System.out.println(c[0]);
		
		

	}

}

大衍数列

    中国古代文献中，曾记载过“大衍数列”, 主要用于解释中国传统文化中的太极衍生原理。

    它的前几项是：0、2、4、8、12、18、24、32、40、50 ...

    其规律是：对偶数项，是序号平方再除2，奇数项，是序号平方减1再除2。

    以下的代码打印出了大衍数列的前 100 项。

for(int i=1; i<100; i++)
{
	if(________________)  //填空
		System.out.println(i*i/2);
	else
		System.out.println((i*i-1)/2);
}

    请填写划线部分缺失的代码。通过浏览器提交答案。

注意：不要填写题面已有的内容，也不要填写任何说明、解释文字。

白痴题：
i % 2 == 0

圆周率

数学发展历史上，圆周率的计算曾有许多有趣甚至是传奇的故事。其中许多方法都涉及无穷级数。

图1.png中所示，就是一种用连分数的形式表示的圆周率求法。

下面的程序实现了该求解方法。实际上数列的收敛对x的初始值 并不敏感。	

结果打印出圆周率近似值（保留小数点后4位，并不一定与圆周率真值吻合）。

/*
整体思维 当n=1时，得到x=2+1/x' x'就是分母的那一大块
pi=4/(x-1)
*/
package 第五届;

public class t04_圆周率 {

	public static void main(String[] args) {
		double x = 111; 
		for(int n = 10000; n>=0; n--){
		int i = 2 * n + 1;
		//System.out.println(i);
		x = 2 + (i*i / x);
		//System.out.println(x+" :");
		}
		System.out.println(String.format("%.4f",4/(x-1)));
	}

}

在这里插入图片描述

奇怪的分式

/*
    上小学的时候，小明经常自己发明新算法。一次，老师出的题目是：

    1/4 乘以 8/5 

    小明居然把分子拼接在一起，分母拼接在一起，答案是：18/45 （参见图1.png）

    老师刚想批评他，转念一想，这个答案凑巧也对啊，真是见鬼！

    对于分子、分母都是 1~9 中的一位数的情况，还有哪些算式可以这样计算呢？

    请写出所有不同算式的个数（包括题中举例的）。

    显然，交换分子分母后，例如：4/1 乘以 5/8 是满足要求的，这算做不同的算式。

    但对于分子分母相同的情况，2/2 乘以 3/3 这样的类型太多了，不在计数之列!

注意：答案是个整数（考虑对称性，肯定是偶数）。请通过浏览器提交。不要书写多余的内容。
*/

/*
i/j  *  k/m=(i*10+k)/(j*10+m)

转/除法为乘法即满足：
i*k*(j*10+m)=j*m*(i*10+k)

*/
package 第五届;

public class t06_奇怪的分数 {
	
	public static void main(String[] args) {
		int cnt=0;
		for(double i=1;i<=9;i++) {//枚举第一个数的分子
			for(double j=1;j<=9;j++) {//枚举第一个数的分母
				if(i==j) continue;
				for(double k=1;k<=9;k++) {
					for(double m=1;m<=9;m++) {
						if(k==m) continue;
						double first=i*k*(10*j+m);
						double last=j*m*(10*i+k);
						if(first==last) {
							cnt++;
							System.out.println(first);
						}
					}
				}
			}
		}
		System.out.println(cnt);

	}

}

扑克序列

/*


A A 2 2 3 3 4 4， 一共4对扑克牌。请你把它们排成一行。
要求：两个A中间有1张牌，两个2之间有2张牌，两个3之间有3张牌，两个4之间有4张牌。

请填写出所有符合要求的排列中，字典序最小的那个。

例如：22AA3344 比 A2A23344 字典序小。当然，它们都不是满足要求的答案。


请通过浏览器提交答案。“A”一定不要用小写字母a，也不要用“1”代替。字符间一定不要留空格。

25314876 对应 4A3A2432
51237468 对应 2342A3A4
字典序最小的是2342A3A4
 */

package 第五届;

import java.util.Arrays;

public class t07_扑克序列_暴力枚举 {

	public static void main(String[] args) {
		for(int ia=1;ia<=6;ia++) {
			for(int i2=1;i2<=5;i2++) {
				for(int i3=1;i3<=4;i3++) {
					for(int i4=1;i4<=3;i4++) {
						int i5=ia+2;int i6=(i2+3);
						int i7=(i3+4);int i8=(i4+5);
					
						String s=""+ia+i2+i3+i4+i5+i6+i7+i8;
						//只要各下标不相等 那么就是一个合法解
						boolean flag=true;
						if(ia==i2||ia==i3||ia==i4||ia==i6||ia==i7||ia==i8||
								i2==i3||i2==i4||i2==i5||i2==i7||i2==i8||
								i3==i4||i3==i5||i3==i6||i3==i8||
								i4==i5||i4==i6||i4==i7||
								i5==i6||i5==i7||i5==i8||
								i6==i7||i6==i8||
								i7==i8
								
							) {
							flag=false;
							break;
						}
						if(flag) {
							System.out.println(s);
						}
					}
				}
				
			}
		}
		for(int ma = 1 ; ma <= 6 ; ma++){
			for(int m2 = 1 ; m2 <= 5 ; m2++){
				for(int m3 = 1 ; m3 <= 4 ; m3++){
					for(int m4 = 1 ; m4 <= 3 ; m4++){
						String str = "" +ma+m2+m3+m4+(ma+2)+(m2+3)+(m3+4)+(m4+5) ;
						//split("")将下标逐个分开作为getStr的元素
						String[] getStr = str.split("");
						boolean flag = true ;
						//将下标从小到大排序
						Arrays.sort(getStr);
					
						for (int i = 0; i < getStr.length-1; i++) {
							if(getStr[i].equals(getStr[i+1])){
								flag = false ;
								break ;
							}
						}
						if(flag){
							System.out.println(str);
						}
					}
				}
			}
		}

	}

}

/*
 dfs全排列+check剪枝
 
 */
package 第五届;

public class t07_扑克序列_深搜剪枝 {
	static char pork[]= {'A','A','2','2','3','3','4','4'};
	static boolean vis[]=new boolean[8];
	static void dfs(int cnt,String s) {
		//System.out.println(index+" "+s);
		if(cnt==8) {
			if(check(s)) {
				System.out.println(s);
				s="";
			}
			return;
		}
		for(int k=0;k<8;k++) {
			if(!vis[k]) {
				vis[k]=true;
				dfs(cnt+1,s+pork[k]);
				vis[k]=false;
			}
		}
	}
	private static boolean check(String s) {
		if(s.lastIndexOf('A')-s.indexOf('A')==2&&
			s.lastIndexOf('2')-s.indexOf('2')==3&&
			s.lastIndexOf('3')-s.indexOf('3')==4&&
			s.lastIndexOf('4')-s.indexOf('4')==5) {
			return true;
		}
		return false;
	}

	public static void main(String[] args) {
		dfs(0,"");
	}

}

package 第五届;

public class t07_扑克序列_交换深搜 {
	
	static void dfs(char[] pork,int index) {
		//System.out.println(s+" "+cnt);
		if(index==8) {
			String s=new String(pork);
			if(check(s)) {
				System.out.println(s);
				
			}
			return;
		}
		for(int i=index;i<8;i++) {
			char c=pork[index];
			pork[index]=pork[i];
			pork[i]=c;
			
			dfs(pork,index+1);
			
			c=pork[i];
			pork[i]=pork[index];
			pork[index]=c;
		}
		
		
	}

	private static boolean check(String s) {
		if(s.lastIndexOf('A')-s.indexOf('A')==2&&
			s.lastIndexOf('2')-s.indexOf('2')==3&&
			s.lastIndexOf('3')-s.indexOf('3')==4&&
			s.lastIndexOf('4')-s.indexOf('4')==5) {
			return true;
		}
		return false;
	}

	public static void main(String[] args) {
		char[] pork= {'2','2','3','3','4','4','A','A'};
		dfs(pork,0);

	}

}

分糖果



/*

有n个小朋友围坐成一圈。老师给每个小朋友随机发偶数个糖果，然后进行下面的游戏：

每个小朋友都把自己的糖果分一半给左手边的孩子。

一轮分糖后，拥有奇数颗糖的孩子由老师补给1个糖果，从而变成偶数。

反复进行这个游戏，直到所有小朋友的糖果数都相同为止。

你的任务是预测在已知的初始糖果情形下，老师一共需要补发多少个糖果。

【格式要求】

    程序首先读入一个整数N(2<N<100)，表示小朋友的人数。
    接着是一行用空格分开的N个偶数（每个偶数不大于1000，不小于2）
    要求程序输出一个整数，表示老师需要补发的糖果数。

例如：输入
3
2 2 4
程序应该输出：
4

这题个人觉得表述实在不严谨 没有说小朋友时顺时针绕圈坐还是逆时针 我按顺时针来结果不对
看了网上的题解是逆时针 对于一半的表示也没有说清楚 当小朋友有奇数颗糖时该怎么分 这里就默认处理了  
 */

package 第五届;

import java.util.Scanner;

public class t08_分糖果2 {
	static boolean check(int [] arra) {
		for (int i = 0; i < arra.length-1; i++) {
			if(arra[i]!=arra[i+1]) {
				return false;
			}
		}
		return true;
	}
	public static void main(String[] args) {
		Scanner reader=new Scanner(System.in);
		int n=reader.nextInt();
		int [] dp=new int[n];
		for (int i = 0; i < n; i++) {
			dp[i]=reader.nextInt();
		}
		int ans=0;
		while(true) {
			int t=dp[0];
			for(int i=0;i<n-1;i++) {
				dp[i]-=dp[i]/2;
				dp[i]+=dp[i+1]/2;
				if((dp[i]&1)==1) {
					ans++;
					dp[i]++;
				}
			}
			dp[n-1]-=dp[n-1]/2;
			dp[n-1]+=t/2;
			if((dp[n-1]&1)==1) {
				dp[n-1]++;
				ans++;
			}
			if(check(dp)) {
				System.out.println(ans);
				break;
			}
				
		}
	}

}

地宫取宝

【题目描述】

   X 国王有一个地宫宝库。是 n x m 个格子的矩阵。每个格子放一件宝贝。每个宝贝贴着价值标签。

    地宫的入口在左上角，出口在右下角。

    小明被带到地宫的入口，国王要求他只能向右或向下行走。

    走过某个格子时，如果那个格子中的宝贝价值比小明手中任意宝贝价值都大，小明就可以拿起它（当然，也可以不拿）。

    当小明走到出口时，如果他手中的宝贝恰好是k件，则这些宝贝就可以送给小明。

    请你帮小明算一算，在给定的局面下，他有多少种不同的行动方案能获得这k件宝贝。

【数据格式】

    输入一行3个整数，用空格分开：n m k (1<=n,m<=50, 1<=k<=12)

    接下来有 n 行数据，每行有 m 个整数 Ci (0<=Ci<=12)代表这个格子上的宝物的价值

    要求输出一个整数，表示正好取k个宝贝的行动方案数。该数字可能很大，输出它对 1000000007 取模的结果。

例如，输入：
2 2 2
1 2
2 1
程序应该输出：
2

再例如，输入：
2 3 2
1 2 3
2 1 5
程序应该输出：
14

【思路】
带条件dfs+mod运算
这里的dfs与以往的不太一样加了一点条件我叫他做带条件的dfs：这里是规定只能向下或向右因此不必担心走回头路的问题
不用vis数组标记

这题有个地方还比较坑就是拿起那个格子的宝贝的前提是：那个格子中的宝贝价值比小明手中任意宝贝价值都大
因此要用一个变量来维护手中的宝贝最大值另外还注意的一点是：价值的取值是从零开始的意味着0也是可取的
再需要注意的一点是：一开始我少考虑到出口时只拿到了k-1件宝贝所以第二个样例怎么算都是5

这样拿到官网上去跑也只能的一半的分


package 第五届;

import java.util.Scanner;

public class t09_地宫取宝_dfs  {
	static int [][] map;
	static int ans=0;
	static int n,m,k;
	public static void dfs(int x,int y,int max,int cnt) {
		//System.out.println(x+" "+y+" "+cnt);
		if(x>=n||y>=m||cnt>k)
			return;
		int cur=map[x][y];
		if(x==n-1&&y==m-1) {
			if(cnt==k) {
				ans=(ans+1)%1000000007;
			}
			if(cnt==k-1&&cur>max) {
				ans=(ans+1)%1000000007;
			}
			return;
		}
	

		if(cur>max) {//大于才可能选
			dfs(x+1,y,cur,cnt+1);
			dfs(x,y+1,cur,cnt+1);
		}//不论大于不大都不选
		dfs(x+1,y,max,cnt);
		dfs(x,y+1,max,cnt);

	
		
	}

	public static void main(String[] args) {
		Scanner reader=new Scanner(System.in);
		
			n=reader.nextInt();
			m=reader.nextInt();
			k=reader.nextInt();
			map=new int[n][m];

			for (int i = 0; i < n; i++) {
				for (int j = 0; j < m; j++) {
					map[i][j]=reader.nextInt();
				}
			}
			dfs(0,0,-1,0);
			System.out.println(ans);
			
		
	}

}

思路：记忆型dfs+mod运算
价值的取值是从零开始的意味着0也是可取的
因此记忆型数组的值要全部初始化为-1
但是还存在一个问题就是一开始max传-1进去数组下标会越界
因而要将max这个维度开大一个也就是-1位置对应0

package 第五届;

import java.util.Scanner;

public class t09_地宫取宝_记忆dfs  {
	static int [][] map;
	static int n,m,k;
	static long [][][][] memo=new long [51][51][14][13];//n m CI k四个维度
	static final long mod=1000000007;
	public static long dfs(int x,int y,int max,int cnt) {
		if(x>=n||y>=m||cnt>k)
			return 0;
		//计算前先查询
		if(memo[x][y][max+1][cnt]!=-1) {
			return memo[x][y][max+1][cnt];
		}
		int cur=map[x][y];
		long ans=0;
		if(x==n-1&&y==m-1) {
			if(cnt==k||(cnt==k-1&&cur>max)) {
				ans++;
			}
			return ans%=mod;
		}


		if(cur>max) {//大于才可能选
			ans+=dfs(x+1,y,cur,cnt+1);
			ans+=dfs(x,y+1,cur,cnt+1);
		}//不论大于不大都不选
		ans+=dfs(x+1,y,max,cnt);
		ans+=dfs(x,y+1,max,cnt);
		
		memo[x][y][max+1][cnt]=ans%mod;
		return memo[x][y][max+1][cnt];

	
		
	}

	public static void main(String[] args) {
			Scanner reader=new Scanner(System.in);
		while(true) {
			n=reader.nextInt();
			m=reader.nextInt();
			k=reader.nextInt();
			map=new int[n][m];

			for (int i = 0; i < n; i++) {
				for (int j = 0; j < m; j++) {
					map[i][j]=reader.nextInt();
				}
			}
			//初始化记忆数组
			for (int i = 0; i < 51; i++) {
				for (int j = 0; j <51; j++) {
					for (int k = 0; k < 14; k++) {
						for (int p = 0; p < 13; p++) {
							memo[i][j][k][p]=-1;
						}
					}
				}
			}
			System.out.println(dfs(0,0,-1,0));
		}
		
	}

}

矩阵翻硬币

/*
问题描述
小明先把硬币摆成了一个 n 行 m 列的矩阵。
随后，小明对每一个硬币分别进行一次 Q 操作。
对第x行第y列的硬币进行 Q 操作的定义：将所有第 i*x 行，第 j*y 列的硬币进行翻转。
其中i和j为任意使操作可行的正整数，行号和列号都是从1开始。
当小明对所有硬币都进行了一次 Q 操作后，他发现了一个奇迹——所有硬币均为正面朝上。
小明想知道最开始有多少枚硬币是反面朝上的。于是，他向他的好朋友小M寻求帮助。
聪明的小M告诉小明，只需要对所有硬币再进行一次Q操作，即可恢复到最开始的状态。
然而小明很懒，不愿意照做。于是小明希望你给出他更好的方法。帮他计算出答案。

输入格式
　　输入数据包含一行，两个正整数 n m，含义见题目描述。
输出格式
　　输出一个正整数，表示最开始有多少枚硬币是反面朝上的。
样例输入
2 3
样例输出
1
数据规模和约定
　　对于10%的数据，n、m <= 10^3；
　　对于20%的数据，n、m <= 10^7；
　　对于40%的数据，n、m <= 10^15；
　　对于100%的数据，n、m <= 10^1000（10的1000次方）。

参考文章:Java蓝桥杯历届试题矩阵翻硬币

gg 不会 看了题解 基本是道数学题 
思路是：
通过硬币被翻的次数来确定是正面朝上还是反面朝上 
如果一枚硬币总共被翻了奇数次最终正面 那么原来状态肯定是反面朝上
对于一枚硬币 需要同时考虑行x和列y 也就是说它会被翻： 行x的被翻的次数（假设为a）乘以列y被翻的次数（假设为b）
因此a、b需均为奇数  而完全平方数有奇数个约数 也就是说 x、y均为完全平方数（完全平方数就是n^2，n为自然数，也就是0，2，4，9……）
因此问题转化为求完全平方数

 


package 第五届;

import java.math.BigInteger;
import java.util.Arrays;
import java.util.Scanner;

public class 矩阵翻硬币 {

	public static void main(String[] args) {
		Scanner reader=new Scanner(System.in);
		String n=reader.next();
		String m=reader.next();
		System.out.println(sqrt(n).multiply(sqrt(m)));
	}
	private static BigInteger sqrt(String s) {
		//被开方数的位数
		int length=s.length();
		
		//被开方数 约数的位数
		int len=0;
		
		if((length&1)==0)
			len=length/2;
		else
			len=length/2+1;
		
		char[] sArr=new char[len];
		Arrays.fill(sArr, '0');
		BigInteger target = new BigInteger(s);
		//逐位试填
		for(int i=0;i<len;i++) {
			for(char a='1';a<='9';a++) {
				sArr[i]=a;
				BigInteger bigInteger = new BigInteger(String.valueOf(sArr)).pow(2);
				if(bigInteger.compareTo(target)==1) {//试探的平方数更大 则回退一位
					sArr[i]-=1;
					break;
				}
			}
		}
		return new BigInteger(String.valueOf(sArr));
	}

}