这网课作业它咋就这么多嘞。。。我咋觉得这届真题断断续续写了半个多世纪嘞。。
| 题目 | 用到知识点/算法类型 |
|---|---|
| 煤球数目 | 递推 数学规律 |
| 生日蜡烛 | 枚举 |
| 凑算式 | 凑算式类dfs |
| 分小组 | dfs+回溯+剪枝 |
| 抽签 | 排列组合类dfs+回溯 |
| 方格填数 | 迷宫类dfs |
| 剪邮票 | 不重复全排列+dfs判连通块 |
| 四平方和 | dfs凑算式+ |
| 取球博弈 | 博弈 dfs |
| 压缩变换 | 枚举+set判重 优化为区间树求区间和+二分法查询 |
煤球数目
有一堆煤球,堆成三角棱锥形。具体:
第一层放1个,
第二层3个(排列成三角形),
第三层6个(排列成三角形),
第四层10个(排列成三角形),
....
如果一共有100层,共有多少个煤球?
请填表示煤球总数目的数字。
注意:你提交的应该是一个整数,不要填写任何多余的内容或说明性文字。
思路
n: 1 2 3 4 5 6 7 8 9 10
f(n) 1 3 6 10 15 21 28 36 45 55
f(1)=1
f(2)=f(1)+2
f(3)=f(2)+3
……
递推式:
f(n)=f(n-1)+n
答案:
171700
package 第七届;
/**
* @author JohnnyLin
* @version Creation Time:2020年5月10日 下午1:32:03
*/
public class t01_煤球数目 {
public static void main(String[] args) {
int a[]=new int[101];
a[1]=1;
int sum=a[1];
for(int i=2;i<a.length;i++) {
a[i]=a[i-1]+i;
sum+=a[i];
}
//System.out.println(a[100]);
System.out.println(sum);
}
}
生日蜡烛
某君从某年开始每年都举办一次生日party,并且每次都要吹熄与年龄相同根数的蜡烛。
现在算起来,他一共吹熄了236根蜡烛。
请问,他从多少岁开始过生日party的?
请填写他开始过生日party的年龄数。
注意:你提交的应该是一个整数,不要填写任何多余的内容或说明性文字。
/*
答案:26
(26+33)*8/2=59*4=236
*/
package 第七届;
/**
* @author JohnnyLin
* @version Creation Time:2020年5月10日 下午1:55:53
*/
public class t02_生日蜡烛 {
public static void main(String[] args) {
//boolean flag = false;
for(int begin=1;begin<150;begin++) {
for(int now=begin+1;now<150;now++) {
if((begin+now)*(now-begin+1)/2==236) {
System.out.println(begin+" "+now);
// flag=true;
break;
}
}
// if(flag) {
// break;
// }
}
}
}
凑算式
B DEF
A + --- + ------- = 10
C GHI
(如果显示有问题,可以参见【图1.jpg】)
这个算式中A~I代表1~9的数字,不同的字母代表不同的数字。
比如:
6+8/3+952/714 就是一种解法,
5+3/1+972/486 是另一种解法。
这个算式一共有多少种解法?
注意:你提交应该是个整数,不要填写任何多余的内容或说明性文字。
错误代码
【思路】
排列问题,
用到知识点:
1、常规dfs套路:
dfs(int index,int cnt)
每个数字只能出现一次 使用vis数组表示
dfs出口:在9个数字都选完的基础上 满足算式 ans++
注意:
计算机中无法精确的表示小数,因此使用除法,即使 使用double类型保证精度 ,也会出现很大误差,如循环小数被四舍五入了。因而得到252的错误答案。正确做法是将除法表达式转为乘法。
package 第七届;
/**
* @author JohnnyLin
* @version Creation Time:2020年5月10日 下午2:05:13
*/
public class t03_凑算式_dfs {
static int ans=0;
static double a[]=new double[10];
static boolean vis[]=new boolean[10];
/**
* @param index 当前为a的index位置选数字
* @param cnt 当前选了cnt个数
*/
static void dfs(int index,int cnt) {
//9个数都选好了
if(cnt==9) {
if(a[1]+a[2]/a[3]+ (a[4]*a[5]*a[6])/(a[7]*a[8]*a[9])==10.0) {
System.out.println(a[1]+" "+a[2]/a[3]+" "+ (a[4]*a[5]*a[6])/(a[7]*a[8]*a[9]));
ans++;
return;
}
}
for(int i=1;i<=9;i++) {
//当前a的index位置选了i
if(!vis[i]) {
a[index]=(double)i;
vis[i]=true;
dfs(index+1,cnt+1);
a[index]=0.0;//可以不用 因为每次选值都会重新覆盖
vis[i]=false;
}
}
}
public static void main(String[] args) {
dfs(1,0);
System.out.println(ans);
}
}
正解
【思路】
精度问题
B DEF
A + — + ------- = 10
C GHI
要转换成乘法:(10 - A)* CGHI = BGHI + DEF * C
package 第七届;
/**
* @author JohnnyLin
* @version Creation Time:2021年4月13日 下午11:59:21
*/
public class t03_凑算式 {
static int N = 9;
static int f[] = new int[N];
static int ans = 0;
static boolean st[] = new boolean[N + 1];
public static void dfs(int u) {
if( u == N) {
int a = f[6]*100+f[7]*10+f[8]; //GHI
int b = (10 - f[0])* (f[2] * a); // (10 - A)* C*GHI
int c = f[1] * a + (f[3] *100 + f[4]*10+f[5])*f[2];
if( b == c) ans++;
return;
}
for(int i = 1; i <= N; i ++)
if( !st[i]) {
st[i] = true;
f[u] = i;
dfs( u + 1);
st[i] = false;
}
}
public static void main(String[] args) {
dfs(0);
System.out.println(ans);
}
}
分小组
9名运动员参加比赛,需要分3组进行预赛。
有哪些分组的方案呢?
我们标记运动员为 A,B,C,... I
下面的程序列出了所有的分组方法。
该程序的正常输出为:
ABC DEF GHI
ABC DEG FHI
ABC DEH FGI
ABC DEI FGH
ABC DFG EHI
ABC DFH EGI
ABC DFI EGH
ABC DGH EFI
ABC DGI EFH
ABC DHI EFG
ABC EFG DHI
ABC EFH DGI
ABC EFI DGH
ABC EGH DFI
ABC EGI DFH
ABC EHI DFG
ABC FGH DEI
ABC FGI DEH
ABC FHI DEG
ABC GHI DEF
ABD CEF GHI
ABD CEG FHI
ABD CEH FGI
ABD CEI FGH
ABD CFG EHI
ABD CFH EGI
ABD CFI EGH
ABD CGH EFI
ABD CGI EFH
ABD CHI EFG
ABD EFG CHI
..... (以下省略,总共560行)。
仔细阅读代码,填写划线部分缺少的内容。
注意:不要填写任何已有内容或说明性文字。
package 第七届;
/**
* @author JohnnyLin
* @version Creation Time:2020年5月10日 下午2:33:13
*/
public class t04_分小组
{
public static String remain(int[] a)
{
String s = "";
for(int i=0; i<a.length; i++){
if(a[i] == 0) s += (char)(i+'A');
}
return s;
}
public static void f(String s, int[] a)
{
for(int i=0; i<a.length; i++){
if(a[i]==1) continue;
a[i] = 1;
for(int j=i+1; j<a.length; j++){
if(a[j]==1) continue;
a[j]=1;
for(int k=j+1; k<a.length; k++){
if(a[k]==1) continue;
a[k]=1;
System.out.println(s+" "+ (char)(i+'A') + (char)(j+'A')+(char)(k+'A')+" "+remain(a)); //填空位置
a[k]=0;
}
a[j]=0;
}
a[i] = 0;
}
}
public static void main(String[] args)
{
int[] a = new int[9];
a[0] = 1;
for(int b=1; b<a.length; b++){
a[b] = 1;
for(int c=b+1; c<a.length; c++){
a[c] = 1;
String s = "A" + (char)(b+'A') + (char)(c+'A');
f(s,a);
a[c] = 0;
}
a[b] = 0;
}
}
}
抽签
X星球要派出一个5人组成的观察团前往W星。
其中:
A国最多可以派出4人。
B国最多可以派出2人。
C国最多可以派出2人。
....
那么最终派往W星的观察团会有多少种国别的不同组合呢?
下面的程序解决了这个问题。
数组a[] 中既是每个国家可以派出的最多的名额。
程序执行结果为:
DEFFF
CEFFF
CDFFF
CDEFF
CCFFF
CCEFF
CCDFF
CCDEF
BEFFF
BDFFF
BDEFF
BCFFF
BCEFF
BCDFF
BCDEF
....
(以下省略,总共101行)
仔细阅读代码,填写划线部分缺少的内容。
注意:不要填写任何已有内容或说明性文字。
package 第七届;
/**
* @author JohnnyLin
* @version Creation Time:2020年5月10日 下午2:40:32
*/
public class t05_抽签
{
public static void f(int[] a, int k, int n, String s)
{
if(k==a.length){
if(n==0) System.out.println(s);
return;
}
String s2 = s;
for(int i=0; i<=a[k]; i++){
f(a,k+1,n-i,s2); //填空位置
s2 += (char)(k+'A');
}
}
public static void main(String[] args)
{
int[] a = {4,2,2,1,1,3};
f(a,0,5,"");
}
}
方格填数
如下的10个格子
+--+--+--+
| | | |
+--+--+--+--+
| | | | |
+--+--+--+--+
| | | |
+--+--+--+
(如果显示有问题,也可以参看【图1.jpg】)
填入0~9的数字。同一数字不能重复填。要求:连续的两个数字不能相邻。
(左右、上下、对角都算相邻)
一共有多少种可能的填数方案?
请填写表示方案数目的整数。
注意:你提交的应该是一个整数,不要填写任何多余的内容或说明性文字。
/*
这题和经典的N皇后问题 、数字九宫格这两个题目比较像
不过这里首先要把map[0][0]和map[2][3]位置筛掉
就是用 不能与(0-9)相差为1的数字先填上(如-2等等)
才不会造成左右、上下、对角相邻位置为相邻数字的影响
可能用到知识点:
1、常见的dfs迷宫类的套路了:
0-9数字 不能重复使用 -------vis标记数组
先按y方向逐个填数字dfs(x,y+1)
当y==4(注意边界 边界为超出时的临界)时 换行 dfs(x+1,0)
这里判断该方格填的数i是否合法的方法时:八个方向逐个检验
dfs出口为 x,y坐标为2,3
注意:
1、要注意一定要先将map初始化为-3 消除干扰
否则会发现答案只有1579少了一种
*/
package 第七届;
/**
* @author JohnnyLin
* @version Creation Time:2020年5月10日 下午3:00:13
*/
public class t06_方格填数 {
static int map[][]=new int[3][4];
static int ans;
//上 左上 ……逆时针方向
static int dir[][]=new int[][]{{-1,0},{-1,-1},{0,-1},{1,-1},{1,0},{1,1},{0,1},{-1,1}};
//标记0-9数字是否用过
private static boolean[] vis=new boolean[10];
/**
* @param x
* @param y
* 当前准备在(x,y)这个方格填数
*/
static void dfs(int x,int y) {
//System.out.println(x+" "+y);
if(x==2&&y==3) {
show(map);
ans++;
return;
}
if(y==4) {
dfs(x+1,0);
return;
}
//往每一个格子填数 且不能重复 因此要使用标记
for(int i=0;i<=9;i++) {
if(!vis[i]&&check(x,y,i)) {
vis[i]=true;
map[x][y]=i;
dfs(x,y+1);
vis[i]=false;
map[x][y]=-3;
}
}
}
private static void show(int[][] map2) {
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 4; j++) {
if((i==0&&j==0)||(i==2&&j==3))
continue;
System.out.print(map2[i][j]+" ");
}
}
System.out.println();
}
//从该位置出发 八个方向扫描 检查是否为相邻数字
private static boolean check(int x, int y, int k) {
for(int i=0;i<8;i++) {
int dx=x+dir[i][0];
int dy=y+dir[i][1];
if(in(dx,dy)) {
if(Math.abs(map[dx][dy]-k)==1) {
return false;
}
}
}
return true;
}
private static boolean in(int x, int y) {
return x>=0&&x<3&&y>=0&&y<4;
}
public static void main(String[] args) {
//因为数字是在0-9之间的 数组默认初始值为0 会与1形成相邻 因而要消除干扰
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 4; j++) {
map[i][j]=-3;
}
}
show(map);
dfs(0,1);
System.out.println(ans);
}
}
剪邮票
图1
图2
图3
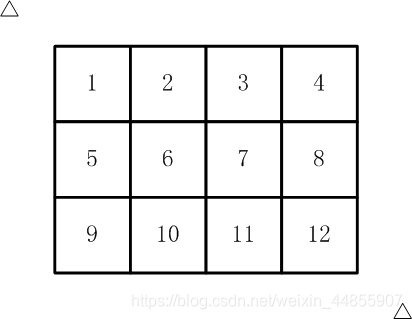
如【图1.jpg】, 有12张连在一起的12生肖的邮票。
现在你要从中剪下5张来,要求必须是连着的。
(仅仅连接一个角不算相连)
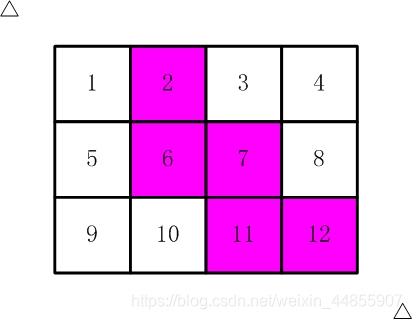
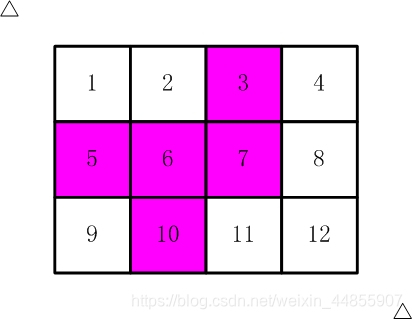
比如,【图2.jpg】,【图3.jpg】中,粉红色所示部分就是合格的剪取。
请你计算,一共有多少种不同的剪取方法。
请填写表示方案数目的整数。
注意:你提交的应该是一个整数,不要填写任何多余的内容或说明性文字。
/*
这题一开始是想对二维数组的每一个点进行步长为5的dfs 但仔细分析给出的图例发现不行
dfs搜出来的5个块虽然是联通的 但形状只能是L类型 因为dfs是一路走到黑 一次不能走两条路是走不出像T字形这种形状
可能是深搜的题做太多了 思维有些定势 觉得很像 总往dfs、bfs这方面想
后来网上搜了题解 才发现这题原来可以:不重复全排列+dfs判连通块来做
答案:116
*
*/
package 第七届;
/**
* @author JohnnyLin
* @version Creation Time:2020年5月10日 下午3:25:53
*/
public class t07_剪邮票 {
private static int ans;
private static int[] a= {0,0,0,0,0,0,0,1,1,1,1,1};
private static boolean[] vis=new boolean[12];
static void permutation(int cnt,int []path) {
if(cnt==12) {
if(check(path)) {
ans++;
}
return;
}
//不重复的全排列
for(int i=0;i<12;i++) {
if(i>0&&a[i]==a[i-1]&&!vis[i-1])
continue;
if(!vis[i]) {
vis[i]=true;
path[cnt]=a[i];
permutation(cnt+1, path);
vis[i]=false;
}
}
}
static void dfs(int x,int y,int [][]map) {
if(x<0||x>=3||y<0||y>=4||map[x][y]!=1)
return;
//该位置置为0
map[x][y]=0;
dfs(x-1,y,map);
dfs(x,y-1,map);
dfs(x+1,y,map);
dfs(x,y+1,map);
}
private static boolean check(int[] path) {
int map[][]=new int[3][4];
//将已经标记好的一维数组转化为对应的二维数组
for (int i = 0; i < 3; i++) {
for (int j = 0; j <4; j++) {
if(path[i*4+j]==1)
map[i][j]=1;
}
}
int cnt=0;//统计连通块的个数 比如三个(2 2 1)之类
for (int i = 0; i < 3; i++) {
for (int j = 0; j <4; j++) {
if(map[i][j]==1) {
dfs(i,j,map);
cnt++;
}
}
}
return cnt==1;
}
public static void main(String[] args) {
int path[]=new int[12];
permutation(0, path);
System.out.println(ans);
}
}
【思路】
递归枚举组合数(12选5) + flood fill算法判断是否连通
package 第七届;
/**
* @author JohnnyLin
* @version Creation Time:2021年4月14日 下午4:53:28
* 类说明
*/
public class t07_剪邮票2 {
static int N = 12;
static boolean st[][] = new boolean[3][4];
static boolean backup[][] = new boolean[3][4]; //备份数组
static int dir[][]= {{-1,0},{0,1},{1,0},{0,-1}};
static int ans = 0;
/**
* 递归型组合数枚举:12个选5个的选法
* @param u
* @param start
*/
public static void dfs(int u, int start) {
if( u == 5) {
if(check ()) {
ans++;
}
return;
}
for(int i = start; i < N; i ++) {
//一维数字对应到二维位置上
int x = i / 4, y = i % 4;
st[x][y] = true;
dfs(u + 1, i + 1);
st[x][y] = false;
}
}
/**
* 判断一个组合方案是否是一个联通块
* 即被标记的状态数组能否dfs通
* @return
*/
private static boolean check() {
for(int i = 0; i < 3; i ++)
for(int j = 0; j < 4; j ++)
backup[i][j] = st[i][j];
for(int i = 0; i < 3; i ++) {
for(int j = 0; j < 4; j ++) {
if( backup[i][j]) {
return isConnected(i, j) == 5;
}
}
}
return false;
}
private static int isConnected(int x,int y) {
int res = 1;
//标记为访问过
backup[x][y] = false;
for(int i = 0; i < 4; i ++) {
int a = x +dir[i][0], b = y + dir[i][1];
if( a >= 0 && a < 3 && b >= 0 && b < 4 && backup[a][b]) {
res += isConnected(a, b);
}
}
return res;
}
public static void main(String[] args) {
dfs(0, 0);
System.out.println(ans);
}
}
Flood Fill错误写法:
private static void isConnected(int x,int y) {
for(int i = 0; i < 4; i ++) {
int a = x +dir[i][0], b = y + dir[i][1];
if( a >= 0 && a < 3 && b >= 0 && b < 4 ) {
if(backup[a][b]) {
backup[a][b] = false; //是要等到该块相邻的四个块都扩展了才标记该块为false
isConnected(a, b);
}
}
}
}
四平方和
四平方和定理,又称为拉格朗日定理:
每个正整数都可以表示为至多4个正整数的平方和。
如果把0包括进去,就正好可以表示为4个数的平方和。
比如:
5 = 0^2 + 0^2 + 1^2 + 2^2
7 = 1^2 + 1^2 + 1^2 + 2^2
(^符号表示乘方的意思)
对于一个给定的正整数,可能存在多种平方和的表示法。
要求你对4个数排序:
0 <= a <= b <= c <= d
并对所有的可能表示法按 a,b,c,d 为联合主键升序排列,最后输出第一个表示法
程序输入为一个正整数N (N<5000000)
要求输出4个非负整数,按从小到大排序,中间用空格分开
例如,输入:
5
则程序应该输出:
0 0 1 2
再例如,输入:
12
则程序应该输出:
0 2 2 2
再例如,输入:
773535
则程序应该输出:
1 1 267 838
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 3000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
package 第七届;
/**
* @author JohnnyLin
* @version Creation Time:2020年5月10日 下午4:49:03
*/
import java.util.Scanner;
public class t08_四平方数和 {
static int n,root;
static int a[] =new int [4];
static int ans;
/**
* @param index 当前在填a[index]这个元素
* @param k 当前的选的数是k,保证升序
* @param sum 当前的选的所有数的平方和
*/
static void dfs(int index,int k,int sum) {
if(sum>n) {
return;
}
if(index==4) {
if(sum==n) {
System.out.println(a[0]+" "+a[1]+" "+a[2]+" "+a[3]);
System.exit(0);
}
return;
}
//从0到sqrt(n)选一个数
for(int i=k;i<=root;i++) {
a[index]=i;
dfs(index+1,i,sum+i*i);
a[index]=0;
}
}
public static void main(String[] args) {
Scanner reader=new Scanner(System.in);
n=reader.nextInt();
root=(int) Math.sqrt((double)n);
dfs(0,0,0);
}
}
取球博弈
两个人玩取球的游戏。
一共有N个球,每人轮流取球,每次可取集合{n1,n2,n3}中的任何一个数目。
如果无法继续取球,则游戏结束。
此时,持有奇数个球的一方获胜。
如果两人都是奇数,则为平局。
假设双方都采用最聪明的取法,
第一个取球的人一定能赢吗?
试编程解决这个问题。
输入格式:
第一行3个正整数n1 n2 n3,空格分开,表示每次可取的数目 (0<n1,n2,n3<100)
第二行5个正整数x1 x2 ... x5,空格分开,表示5局的初始球数(0<xi<1000)
输出格式:
一行5个字符,空格分开。分别表示每局先取球的人能否获胜。
能获胜则输出+,
次之,如有办法逼平对手,输出0,
无论如何都会输,则输出-
例如,输入:
1 2 3
1 2 3 4 5
程序应该输出:
+ 0 + 0 -
再例如,输入:
1 4 5
10 11 12 13 15
程序应该输出:
0 - 0 + +
再例如,输入:
2 3 5
7 8 9 10 11
程序应该输出:
+ 0 0 0 0
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 3000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
/*
双方的取球可选范围是一样的{n1,n2,n3}
双方都采用最聪明的取法,就是说每个人都尽可能地选择使得自己的总数量为奇数
一开始觉得是动态规划 但写不出dp数组
想不出来-------
网上解法:多分支dfs
有些类似爬楼梯方案数 可选楼梯数是{n1,n2,n3}
但是取球博弈这里存在对手 是交互式选球 你取球面临地总球数是我上一轮选剩下地
我下轮取球面临地总球数是你这轮取完剩下的 因此dfs传参时参数要互换
结算规则:
if:在分支出来地三个局面中存在一个局面对手输 那么我赢了
else if :在对手不输的基础上存在一个局面是平局 那么逼平
else: 我输了
*/
package 第七届;
import java.util.Arrays;
import java.util.Scanner;
/**
* @author JohnnyLin
* @version Creation Time:2020年5月14日 上午9:57:48
*/
public class t09_取球博弈dfs {
static int num[];
private static char dfs(int n, int me, int you) {
//结算规则
if(n<num[0]) {
if((me&1)==1&&(you&1)==0)//你赢 奇数 偶数
return '+';
else if((me&1)==0&&(you&1)==1)//你输 偶数 奇数
return '-';
else //平 奇数 奇数 偶数 偶数
return '0';
}
boolean flag=false;
for(int i=0;i<3;i++) {
if(n>=num[i]) {
//交换身份进行选球
char c=dfs(n-num[i],you,me+num[i]);
//判定输赢规则 c得到是对手输赢情况
if(c=='-')//对手输则我赢
return '+';
if(c=='0')
flag=true;
}
}
//对手不输那么对手可能赢或者平
if(flag)//双方都平
return '0';
else//不平则我输了
return '-';
}
public static void main(String[] args) {
Scanner reader=new Scanner(System.in);
num=new int[3];
for(int i=0;i<3;i++) {
num[i]=reader.nextInt();
}
Arrays.sort(num);
//game数组存放每局球数
int game[]=new int[5];
for(int i=0;i<5;i++) {
game[i]=reader.nextInt();
System.out.print(dfs( game[i],0,0 )+" ");
}
System.out.println();
}
}
package 第七届;
/**
* @author JohnnyLin
* @version Creation Time:2020年5月18日 下午9:46:45
* 类说明
*/
import java.util.Arrays;
import java.util.Scanner;
public class t09_取球博弈记忆型dfs {
static int num[];
//记忆型数组
static char[][][]memo=new char[1000][2][2];
private static char dfs(int n, int me, int you) {
//结算规则
if(n<num[0]) {
if((me&1)==1&&(you&1)==0)//你赢 奇数 偶数
return '+';
else if((me&1)==0&&(you&1)==1)//你输 偶数 奇数
return '-';
else //平 奇数 奇数 偶数 偶数
return '0';
}
//不为空字符则表示该状态已经计算过了 直接返回
if(memo[n][me][you]!='\0')
return memo[n][me][you];
boolean flag=false;
for(int i=0;i<3;i++) {
if(n>=num[i]) {
//交换身份进行选球
//传递奇偶性 当前选的球数为奇数则为1 为偶数则为0 加上偶数则不改变原奇偶性
char c=dfs(n-num[i],you,(num[i]&1)==0?me:(1-me));
//判定输赢规则 c得到是对手输赢情况
if(c=='-')//对手输则我赢
{
memo[n][me][you]='+';
return '+';
}
if(c=='0')
flag=true;
}
}
//对手不输那么对手可能赢或者平
if(flag) { //双方都平
memo[n][me][you]='0';
return '0';
}
else{ //不平则我输了
memo[n][me][you]='-';
return '-';
}
}
public static void main(String[] args) {
Scanner reader=new Scanner(System.in);
num=new int[3];
for(int i=0;i<3;i++) {
num[i]=reader.nextInt();
}
Arrays.sort(num);
//game数组存放每局球数
int game[]=new int[5];
for(int i=0;i<5;i++) {
game[i]=reader.nextInt();
System.out.print(dfs( game[i],0,0 )+" ");
}
System.out.println();
}
}
压缩变换
/*
小明最近在研究压缩算法。
他知道,压缩的时候如果能够使得数值很小,就能通过熵编码得到较高的压缩比。
然而,要使数值很小是一个挑战。
最近,小明需要压缩一些正整数的序列,这些序列的特点是,后面出现的数字很大可能是刚出现过不久的数字。对于这种特殊的序列,小明准备对序列做一个变换来减小数字的值。
变换的过程如下:
从左到右枚举序列,每枚举到一个数字,如果这个数字没有出现过,刚将数字变换成它的相反数,如果数字出现过,则看它在原序列中最后的一次出现后面(且在当前数前面)出现了几种数字,用这个种类数替换原来的数字。
比如,序列(a1, a2, a3, a4, a5)=(1, 2, 2, 1, 2)在变换过程为:
a1: 1未出现过,所以a1变为-1;
a2: 2未出现过,所以a2变为-2;
a3: 2出现过,最后一次为原序列的a2,在a2后、a3前有0种数字,所以a3变为0;
a4: 1出现过,最后一次为原序列的a1,在a1后、a4前有1种数字,所以a4变为1;
a5: 2出现过,最后一次为原序列的a3,在a3后、a5前有1种数字,所以a5变为1。
现在,给出原序列,请问,按这种变换规则变换后的序列是什么。
输入格式:
输入第一行包含一个整数n,表示序列的长度。
第二行包含n个正整数,表示输入序列。
输出格式:
输出一行,包含n个数,表示变换后的序列。
例如,输入:
5
1 2 2 1 2
程序应该输出:
-1 -2 0 1 1
再例如,输入:
12
1 1 2 3 2 3 1 2 2 2 3 1
程序应该输出:
-1 0 -2 -3 1 1 2 2 0 0 2 2
数据规模与约定
对于30%的数据,n<=1000;
对于50%的数据,n<=30000;
对于100%的数据,1 <=n<=100000,1<=ai<=10^9
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 3000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
*/
package 第七届;
import java.util.HashMap;
import java.util.HashSet;
import java.util.Scanner;
/**
* @author JohnnyLin
* @version Creation Time:2020年5月19日 下午5:44:37
*/
/*
* 这样的写法只能通过30%的数据
*/
public class t10_压缩变换 {
public static void main(String[] args) {
Scanner reader=new Scanner(System.in);
int n=reader.nextInt();
int [] data=new int[n];
int ans[] =new int[n];
HashMap <Integer,Integer> lastIndexOf =new HashMap<>();
for(int i=0;i<n;i++) {
data[i]=reader.nextInt();
//第一次出现则 存该数的相反数
if(lastIndexOf.get(data[i])==null) {
ans[i]=-data[i];
}else {
//统计最后一次出现到本次出现这段区间的数字种类
HashSet set=new HashSet<>();
for(int j=lastIndexOf.get(data[i])+1;j<i;j++) {
set.add(data[j]);
}
ans[i]=set.size();
}
lastIndexOf.put(data[i], i);
}
for (int i = 0; i < ans.length; i++) {
System.out.print(ans[i]+" ");
}
}
}
/*
这道题的优化在于统计最后一次出现到本次出现这段区间的数字种类
网上解法如下 时间复杂度为n*log(n)
可以使用区间树来统计两个位置之间的个数 即求区间和
使用区间树查询某一段区间的和 由于使用的是二分法 查询时间复杂度为log(n)
*/
package 第七届;
import java.util.HashMap;
import java.util.Scanner;
/**
* @author JohnnyLin
* @version Creation Time:2020年5月19日 下午5:44:37
*/
public class t10_压缩变换_优化 {
static HashMap <Integer,Integer> lastIndexOf =new HashMap<>();
static int[] a;//记录原始数据
static int [] ans;//记录答案
//01序列 b数组某一个位置p上的数字为1表示a[p]这个数字最后出现的位置是p,a[p]曾经出现过的位置都是0
//求得的区段和即为该区段所有数字的种类数
static int[] b;
private static SegTree root;
public static void main(String[] args) {
Scanner reader=new Scanner(System.in);
int n=reader.nextInt();
//初始化
a=new int[n];
ans =new int[n];
b =new int[n];
//构建区间树
root = buildSegTree(0, n-1);
for(int i=0;i<n;i++) {
int num=reader.nextInt();
a[i]=num;
//该数上一次出现的位置
Integer preIndex=lastIndexOf.get(num);
//第一次出现则 存该数的相反数
if(preIndex==null) {
ans[i]=-num;
b[i]=1;
update(root,i,1);
}else {
//统计最后一次出现到本次出现这段区间的数字种类
ans[i]=query(root,preIndex+1,i-1);
b[preIndex]=0;
b[i]=1;
update(root, preIndex, -1);
update(root, i, 1);
}
lastIndexOf.put(num, i);
}
for (int i = 0; i < ans.length; i++) {
System.out.print(ans[i]+" ");
}
}
private static int query(SegTree tree, int x, int y) {
int l=tree.l;
int r=tree.r;
if(x<=l&&y>=r) return tree.sum;
int mid=(l+r)>>1;
int ans=0;
if(x<=mid) ans+=query(tree.lson,x,y);
if(y>mid) ans+=query(tree.rson,x,y);
return ans;
}
/*构建区间树*/
/**
* @param l 左区间
* @param r 右区间
* @return 区间树
*/
static SegTree buildSegTree(int l,int r) {
SegTree segTree=new SegTree(l,r);
//区间树的叶子结点就是数组b的每一个元素
if(l==r) {
segTree.sum=b[l];
return segTree;
}
int mid=(l+r)>>1;
SegTree lson=buildSegTree(l,mid);
SegTree rson=buildSegTree(mid+1,r);
segTree.lson=lson;
segTree.rson=rson;
segTree.sum=lson.sum+rson.sum;
return segTree;
}
/**
* @param p 下标
* @param i 增量
*/
static void update(SegTree tree,int p,int i) {
if(tree==null) {
return;
}
//更新以tree为根的区间数的区间和
tree.sum+=i;
int l=tree.l;
int r=tree.r;
int mid=(l+r)>>1;
if(p<=mid) {
update(tree.lson,p,i);
}else {//(p>mid)
update(tree.rson,p,i);
}
}
static class SegTree{
int l,r;//区间范围
int sum; //区间和
SegTree lson;//左子树
SegTree rson;//右子树
public SegTree(int l,int r) {
this.l=l;
this.r=r;
}
}
}