这届蓝桥杯,从题目来看,熟悉的搜索类题目明显减少,用到数学知识难度甚至有几道题目还用到数论的一些知识,动态规划、大数运算、排序、dfs、个人感觉这届是试题整体难度是提高了。可能是被骂“暴力杯”,“搜索杯”骂惨了。
| 题目 | 用到知识点/算法类型 |
|---|---|
| 第几天 | 水题 |
| 方格计数 | 数学知识 距离公式 |
| 复数幂 | 大数运算 文件输出 |
| 测试次数 | dp |
| 快速排序 | 排序 |
| 递增三元组 | 排序 双指针 |
| 日志统计 | 排序 自定义一对多数据结构 |
| 全球变暖 | dfs |
| 堆的计数 | 数论知识 快速幂、模运算 |
第几天
标题:第几天
2000年的1月1日,是那一年的第1天。
那么,2000年的5月4日,是那一年的第几天?
注意:需要提交的是一个整数,不要填写任何多余内容。
打开日历
1到5月份填数分别为:31 29 31 30 4
答案:125
方格计数
标题:方格计数
如图p1.png所示,在二维平面上有无数个1x1的小方格。
我们以某个小方格的一个顶点为圆心画一个半径为1000的圆。
你能计算出这个圆里有多少个完整的小方格吗?
注意:需要提交的是一个整数,不要填写任何多余内容。
/*
由于圆是对称的 所以只需要统计正半轴的方格数再乘以4即可得到总数
方格能在圆内实际上就是 方格右上方点到圆心距离小于等于半径
答案:3137548
*/
package 第九届;
/**
* @author JohnnyLin
* @version Creation Time:2020年5月28日 下午8:30:11
* 类说明
*/
public class t02_方格计数 {
public static void main(String[] args) {
int r=1000;
int ans=0;
for (int i = 1; i <= r; i++) {
for (int j = 1; j <= r; j++) {
if(i*i+j*j<=r*r)
ans++;
}
}
System.out.println(ans*4);
}
}
复数幂
标题:复数幂
设i为虚数单位。对于任意正整数n,(2+3i)^n 的实部和虚部都是整数。
求 (2+3i)^123456 等于多少? 即(2+3i)的123456次幂,这个数字很大,要求精确表示。
答案写成 "实部±虚部i" 的形式,实部和虚部都是整数(不能用科学计数法表示),中间任何地方都不加空格,实部为正时前面不加正号。(2+3i)^2 写成: -5+12i,
(2+3i)^5 的写成: 122-597i
注意:需要提交的是一个很庞大的复数,不要填写任何多余内容。
/*
没有想太多 用long去存储 得到4043220979119144065 -7374402350132176768i的错误答案
实际上这题应该使用大数存储 因为2^123456肯定超过long型(2^64)
*/
package 第九届;
import java.io.File;
import java.io.FileNotFoundException;
import java.io.PrintStream;
import java.math.BigInteger;
/**
* @author JohnnyLin
* @version Creation Time:2020年6月2日 下午4:58:28
*/
public class t03_复数幂2 {
public static void main(String[] args) throws FileNotFoundException {
//BigInteger a=new BigInteger();
BigInteger a=BigInteger.valueOf(2);
BigInteger b=BigInteger.valueOf(3);
BigInteger c=BigInteger.valueOf(2);
BigInteger d=BigInteger.valueOf(3);
//根据复数乘法:(a+b*i)*(c+d*i)=(a*c-b*d)+(b*c+a*d)i
for(int i=1;i<=123455;i++) {
//注意此处要借助临时变量存储
BigInteger t=a.multiply(c).subtract(b.multiply(d));
BigInteger k=b.multiply(c).add(a.multiply(d));
c=t;
d=k;
}
/*
* 你以为到这里 直接输出就结束了吗 并没有 直接输出到控制台会发现只有:
* 这是因为数据实在太长了 控制台放不下直接换页了
* 百度搜了一下 采用以下方式将输出结果保存在ans.txt文件
*/
//System.out.println(c.toString()+d.toString());
PrintStream ps = new PrintStream(new File("ans.txt"));//默认在项目的路径
System.setOut(ps);//输出在ans.txt里
System.out.println(c.toString()+d.toString()+"i");
// System.setOut(out);//注释了下面就不会输入到控制台里
//
// System.out.println(a.toString()+b.toString()+"i");
}
}
相似题 斐波那契
import java.math.BigInteger;
/**
* @author JohnnyLin
* @version Creation Time:2021年4月16日 下午5:57:25
*/
public class Main {
public static void main(String[] args) {
int N = 20;
long q[] = new long [N];
long s[] = new long[N];
// 1 1 2 3 5 8 13
q[1] = 1;
q[2] = 1;
for(int i = 3; i <= 14; i ++)
q[i] = q[i - 1] + q[i - 2];
for(int i = 1; i <= 13; i ++)//1 2 6 15 40 104 273 714 1870 4895 12816 33552 87841
s[i] = q[i] * q[i + 1];
// m/x + n/y
//不在原数上进行操作 结果以BigInteger返回
BigInteger x = new BigInteger(String.valueOf(s[1]));
BigInteger m = new BigInteger("1");
BigInteger y = new BigInteger(String.valueOf(s[2]));
BigInteger n = new BigInteger("1");
for(int i = 3; i <= 14; i ++) {
//System.out.println(m +"/" + x + "\t"+ n +"/"+ y);
//分数加法
BigInteger c = y.multiply(m).add(x.multiply(n));
BigInteger d = x.multiply(y);
//通分
BigInteger g = gcd(c,d);
c = c.divide(g);
d = d.divide(g);
x = d;
m = c;
n = new BigInteger("1");
y = new BigInteger(""+s[i]);
}
System.out.println(m +"/" + x );// 6535086616739/3684083162760
}
//手写大数gcd
private static BigInteger gcd(BigInteger a, BigInteger b) {
if( b.compareTo(new BigInteger("0")) == 0 ) return a;
return gcd(b, a.mod(b));
}
}
测试次数
/*
标题:测试次数
x星球的居民脾气不太好,但好在他们生气的时候唯一的异常举动是:摔手机。
各大厂商也就纷纷推出各种耐摔型手机。x星球的质监局规定了手机必须经过耐摔测试,
并且评定出一个耐摔指数来,之后才允许上市流通。
x星球有很多高耸入云的高塔,刚好可以用来做耐摔测试。
塔的每一层高度都是一样的,与地球上稍有不同的是,他们的第一层不是地面,而是相当于我们的2楼。
如果手机从第7层扔下去没摔坏,但第8层摔坏了,则手机耐摔指数=7。
特别地,如果手机从第1层扔下去就坏了,则耐摔指数=0。
如果到了塔的最高层第n层扔没摔坏,则耐摔指数=n
为了减少测试次数,从每个厂家抽样3部手机参加测试。
某次测试的塔高为1000层,如果我们总是采用最佳策略,
在最坏的运气下最多需要测试多少次才能确定手机的耐摔指数呢?
请填写这个最多测试次数。
注意:需要填写的是一个整数,不要填写任何多余内容。
*/
/*
* 注意到测试的次数与手机数和手机耐摔指数有关
* 打表 得到递推关系
* f1(i)=i f1(i)表示只有一台手机耐摔指数为i时最多测试次数为i
* 这是因为只有一台手机 所以只能从1层开始测试起(否则可能会被摔坏 就没手机了)
*
* 这里要理解最坏运气与最优策略
* 所谓最坏运气就是测试次数往最多的方向发展 最优策略时在测试次数往最多方向发展的所有可能种的最小值
*/
package 第九届;
/**
* @author JohnnyLin
* @version Creation Time:2020年5月28日 下午10:15:57
*/
public class t04_测试次数2 {
static final int N=1000;
public static void main(String[] args) {
int f1[]=new int [N+1];
int f2[]=new int [N+1];
int f3[]=new int [N+1];
//一部手机时
for (int i = 1; i <= N; i++) {
f1[i]=i;
}
//两部手机时
//手机耐摔指数为i时
for (int i = 1; i <=N; i++) {
int ans=Integer.MAX_VALUE;
/*枚举开始测试的层数j 每一层测试结果有两种
*1、摔坏了
记住摔了手机数就少了一个 该手机的测试次数为:1+f1[j-1]
2、 或者还是好的 该手机的测试次数为:f2[i-j]
两者取一个max作为该手机在该层开始测试的最多测试次数
最优策略为i层中所有最多测试次数的最小值某一个j值
*/
for (int j = 1; j <=i; j++) {
int max = 1+Math.max(f1[j-1], f2[i-j]);
ans=Math.min(max, ans);
}
f2[i]=ans;
}
//三部手机时
for (int i = 1; i <=N; i++) {
int ans=Integer.MAX_VALUE;
/*枚举开始测试的层数j 每一层测试结果有两种
*1、摔坏了
记住摔了手机数就少了一个 该手机的测试次数为:1+f2[j-1]
2、 或者还是好的 该手机的测试次数为:f3[i-j]
两者取一个max作为该手机在该层开始测试的最多测试次数
最优策略为i层中所有最多测试次数的最小值某一个j值
*/
for (int j = 1; j <=i; j++) {
int max = 1+Math.max(f2[j-1], f3[i-j]);
ans=Math.min(max, ans);
}
f3[i]=ans;
}
System.out.println(f3[N]);
}
}
快速排序
标题:快速排序
以下代码可以从数组a[]中找出第k小的元素。
它使用了类似快速排序中的分治算法,期望时间复杂度是O(N)的。
请仔细阅读分析源码,填写划线部分缺失的内容。
import java.util.Random;
public class Main{
public static int quickSelect(int a[], int l, int r, int k) {
Random rand = new Random();
int p = rand.nextInt(r - l + 1) + l;
int x = a[p];
int tmp = a[p]; a[p] = a[r]; a[r] = tmp;
int i = l, j = r;
while(i < j) {
while(i < j && a[i] < x) i++;
if(i < j) {
a[j] = a[i];
j--;
}
while(i < j && a[j] > x) j--;
if(i < j) {
a[i] = a[j];
i++;
}
}
a[i] = x;
p = i;
if(i - l + 1 == k) return a[i];
if(i - l + 1 < k) return quickSelect( _________________________________ ); //填空
else return quickSelect(a, l, i - 1, k);
}
public static void main(String args[]) {
int [] a = {1, 4, 2, 8, 5, 7};
System.out.println(quickSelect(a, 0, 5, 4));
}
}
注意:只提交划线部分缺少的代码,不要抄写任何已经存在的代码或符号。
package 第九届;
/**
* @author JohnnyLin
* @version Creation Time:2020年5月28日 下午10:26:17
*/
import java.util.Random;
public class t05_快速排序{
/**
1, 4, 2, 8, 5, 7
quickSelect(a, 0, 5, 4)
* @param a 待排序数组
* @param l 左区间下标
* @param r 右区间下标
* @param k
* @return
*/
public static int quickSelect(int a[], int l, int r, int k) {
//随机获得指针
Random rand = new Random();
int p = rand.nextInt(r - l + 1) + l;// 3 3 3 5
//System.out.println(p);
int x = a[p];
//交换a[p]选定元素与右区间元素a[r]
int tmp = a[p]; a[p] = a[r]; a[r] = tmp;
int i = l, j = r;
while(i < j) {
while(i < j && a[i] < x) i++;
if(i < j) {
a[j] = a[i];
j--;
}
while(i < j && a[j] > x) j--;
if(i < j) {
a[i] = a[j];
i++;
}
}
a[i] = x;
//mid
p = i;
if(i - l + 1 == k) return a[i];
//实际名次在右边 a, p+1, r, k-(i-l+1)
//8 6
//3 5
//l=4 r=8
// 2=k-(r-l)=6-(8-4)
//排名k是在该区间的排名 注意这个区间是不断缩小 最后逼近某个元素的
if(i - l + 1 < k) return quickSelect( a, i+1,r, k-(i-l+1)); //填空
else return quickSelect(a, l, i - 1, k);
}
public static void main(String args[]) {
// int [] a = {1, 4, 2, 8, 5, 7};
// System.out.println(quickSelect(a, 0, 5, 4));
int [] a = {1, 4, 2, 8, 5, 7, 0};//0 1 2 4 5 7 8
System.out.println(quickSelect(a, 0, 6, 1));
int [] b = {1, 4, 2, 8, 5, 7, 0};//0 1 2 4 5 7 8
System.out.println(quickSelect(b, 0, 6, 3));
int [] c = {1, 4, 2, 8, 5, 7, 0};//0 1 2 4 5 7 8
System.out.println(quickSelect(c, 0, 6, 6));
}
}
递增三元组
标题:递增三元组
给定三个整数数组
A = [A1, A2, ... AN],
B = [B1, B2, ... BN],
C = [C1, C2, ... CN],
请你统计有多少个三元组(i, j, k) 满足:
1. 1 <= i, j, k <= N
2. Ai < Bj < Ck
【输入格式】
第一行包含一个整数N。
第二行包含N个整数A1, A2, ... AN。
第三行包含N个整数B1, B2, ... BN。
第四行包含N个整数C1, C2, ... CN。
对于30%的数据,1 <= N <= 100
对于60%的数据,1 <= N <= 1000
对于100%的数据,1 <= N <= 100000 0 <= Ai, Bi, Ci <= 100000
【输出格式】
一个整数表示答案
【输入样例】
3
1 1 1
2 2 2
3 3 3
【输出样例】
27
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
不要使用package语句。不要使用jdk1.7及以上版本的特性。
主类的名字必须是:Main,否则按无效代码处理。
3
1 3 1
3 2 5
4 2 6
3
1 1 3
2 3 5
2 4 6
这道题就是从A、B、C三个数组中分别选出一个数a、b、c
使得a<b<c
由于是A、B、C是降序排好序的 使用O(n)的双指针法
1、首先比较B[p]与C[k]
如果k<N&&B[p]>=C[k] k右移直到第一个大于B[p]的位置
2、然后k不动 b[p]记录N-k即C数组中大于B[p]的个数
前缀和数组记录截止到B[p]时 C数组中大于B[p]的个数累加和 s[p]=(p==0?0:s[p-1])+b[p]
3、然后p右移
重复上述步骤 直至p或k>=N。
比较A[i]与B[j]也是类似的
1、首先比较A[i]与B[j]
如果j<N&&A[i]>=B[j] j右移直到第一个大于A[i]的位置
2、然后j不动 ans+=s[N-1]-(j==0?0:s[j-1]) 得到[j,N-1)区间C大于Bd的总个数
3、然后p右移
重复上述步骤 直至i或j>=N
package 第九届;
import java.io.File;
import java.io.FileInputStream;
import java.io.FileNotFoundException;
import java.util.Arrays;
import java.util.Scanner;
/**
* @author JohnnyLin
* @version Creation Time:2020年5月29日 下午8:55:23
*/
public class t06_递增三元组2 {
// static void show(int a[]) {
// for (int i = 0; i < a.length; i++) {
// System.out.print(a[i]+" ");
// }
// System.out.println();
// }
public static void main(String[] args) throws FileNotFoundException {
System.setIn(new FileInputStream(new File("src/data/in8.txt") ) );
Scanner reader=new Scanner(System.in);
int N=reader.nextInt();
int A[]=new int[N];
int B[]=new int[N];
int C[]=new int[N];
int b[]=new int[N];//记录C数组中大于B[i]的个数
long s[]=new long[N];//记录前缀和(累加和) 超过整型范围 用long存储
for (int j = 0; j < N; j++) {
A[j]=reader.nextInt();
}
for (int j = 0; j < N; j++) {
B[j]=reader.nextInt();
}
for (int j = 0; j < N; j++) {
C[j]=reader.nextInt();
}
Arrays.sort(A);
Arrays.sort(B);
Arrays.sort(C);
int p=0;
int k=0;
while(p<N) {
while(k<N&&C[k]<=B[p]) {
k++;
}
b[p]=N-k;
s[p]=(p==0?0:s[p-1])+b[p];
p++;
}
long ans=0;
int i=0;
int j=0;
while(i<N) {
while(j<N&&B[j]<=A[i]) {
j++;
}
ans+=s[N-1]-(j==0?0:s[j-1]);
i++;
}
System.out.println(ans);
}
}
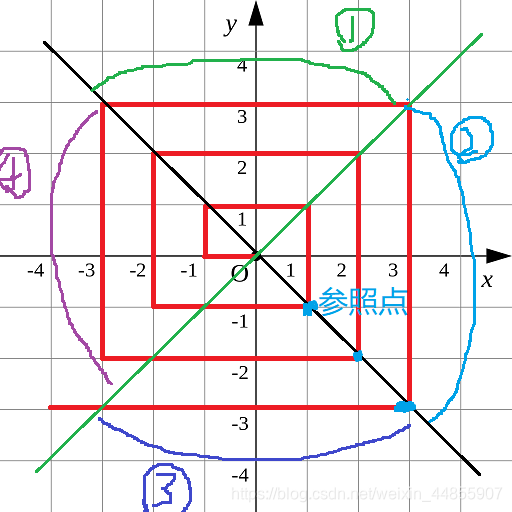
/*
这是一道数学题 得找到规律才能解
以y=-x将螺旋折线 划分为如图两个区域
在右上角区域 每一个所截得的线段长度分别为 4 8 12……
为首项a1=4 公差d=4的等差数列
要计算每一个给定点的dis 即可以以右下角点为参照点
进行step步的位移操作即可得到
右下角点长度为s(n)=(a(1)+a(n))*n/2=a(1)+(n*(n-1)d)/2
*/
package 第九届;
import java.util.Scanner;
/**
* @author JohnnyLin
* @version Creation Time:2020年6月4日 下午1:41:18
*/
public class t07_螺旋折线2 {
public static void main(String[] args) {
Scanner reader=new Scanner (System.in);
//0 1
int X=reader.nextInt();
int Y=reader.nextInt();
long dis=1;
long n=0,ans=0;
//区域一
if(Y>0&&Math.abs(X)<=Y) {
//第几项
n=Y;
//跟右下角参照点的差距
dis=Y-X+2*Y;
}else if(X>0&&Math.abs(Y)<=X) { //区域二
n=X;
dis=Y+X;
}else if(Y<=0&&X>=Y-1&&X<=-Y) {//区域三
n=-Y;
dis=-(-Y-X);
}else if(X<0&&Y>=X+1&&Y<=-X) { //区域四
n=-X-1;
dis=-(Y-X-1-2*X-1);
}
System.out.println(sum(1L,2*n,1)*2-dis);
}
static long sum(long a,long n,int d) {
return (a+a+(n-1)*d)*n/2;
}
}
日志统计
标题:日志统计
小明维护着一个程序员论坛。现在他收集了一份"点赞"日志,日志共有N行。其中每一行的格式是:
ts id
表示在ts时刻编号id的帖子收到一个"赞"。
现在小明想统计有哪些帖子曾经是"热帖"。如果一个帖子曾在任意一个长度为D的时间段内收到不少于K个赞,小明就认为这个帖子曾是"热帖"。
具体来说,如果存在某个时刻T满足该帖在[T, T+D)这段时间内(注意是左闭右开区间)收到不少于K个赞,该帖就曾是"热帖"。 [1,12)
给定日志,请你帮助小明统计出所有曾是"热帖"的帖子编号。
【输入格式】
第一行包含三个整数N、D和K。
以下N行每行一条日志,包含两个整数ts和id。
对于50%的数据,1 <= K <= N <= 1000
对于100%的数据,1 <= K <= N <= 100000 0 <= ts <= 100000 0 <= id <= 100000
【输出格式】
按从小到大的顺序输出热帖id。每个id一行。
【输入样例】
7 10 2
0 1
0 10
10 10
10 1
9 1
100 3
100 3
【输出样例】
1
3
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
不要使用package语句。不要使用jdk1.7及以上版本的特性。
主类的名字必须是:Main,否则按无效代码处理。
/*
先将相同id的帖子 及其收到赞的时间保存下来
要用到一对多结构
id ts
1 0 9 10
3 100 100
10 0 10
然后枚举每一个可能的时间点T 统计[T,T+D)时间内的赞数是否超过K
注意点 :
1、要求从小到大的顺序输出热帖id
*/
package 第九届;
import java.util.Arrays;
import java.util.Scanner;
/**
* @author JohnnyLin
* @version Creation Time:2020年5月30日 下午2:48:40
* 类说明
*/
public class t08_日志统计2 {
//record类存放每条记录对应的时间和id
//record实现comparable接口 以实现每条记录的排序
public static class record implements Comparable<record>{
int id,ts;
record(int id,int ts){
this.id=id;
this.ts=ts;
}
//重写compareTo方法 先按id比较 相同id则按ts比
@Override
public int compareTo(record o) {
if(this.id==o.id)
return this.ts-o.ts;
else
return this.id-o.id;
}
}
public static void main(String[] args) {
Scanner reader=new Scanner(System.in);
int N=reader.nextInt();
int D=reader.nextInt();
int K=reader.nextInt();
//声明一个存放每一条点赞记录的数组
record blog[]=new record[N];
boolean flag[]=new boolean[100000];
for(int i=0;i<N;i++) {
int ts=reader.nextInt();
int id=reader.nextInt();
//每一个blog[i]对应存放一条记录
blog[i]=new record(id,ts);
}
Arrays.sort(blog);
/*
* 排完序之后
1 0
1 9
1 10
3 100
3 100
10 0
10 10
*/
// for(int i=0;i<N;i++) {
// System.out.println(blog[i].id+" "+blog[i].ts);
//
// }
for(int i=0;i+K-1<N;i++) {
int id = blog[i].id;
int next=i+K-1;
//最低要求(至少):相距K-1的那条仍然是相同id 且时间间隔在D范围内
if(!flag[id]&&blog[ next].id==id&& (blog[next].ts-blog[i].ts)<D) {
flag[id]=true;
System.out.println(id);
}
}
}
}
全球变暖
标题:全球变暖
你有一张某海域NxN像素的照片,"."表示海洋、"#"表示陆地,如下所示:
.......
.##....
.##....
....##.
..####.
...###.
.......
其中"上下左右"四个方向上连在一起的一片陆地组成一座岛屿。例如上图就有2座岛屿。
由于全球变暖导致了海面上升,科学家预测未来几十年,岛屿边缘一个像素的范围会被海水淹没。
具体来说如果一块陆地像素与海洋相邻(上下左右四个相邻像素中有海洋),它就会被淹没。
例如上图中的海域未来会变成如下样子:
.......
.......
.......
.......
....#..
.......
.......
请你计算:依照科学家的预测,照片中有多少岛屿会被完全淹没。
【输入格式】
第一行包含一个整数N。 (1 <= N <= 1000)
以下N行N列代表一张海域照片。
照片保证第1行、第1列、第N行、第N列的像素都是海洋。
【输出格式】
一个整数表示答案。
【输入样例】
7
.......
.##....
.##....
....##.
..####.
...###.
.......
【输出样例】
1
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
不要使用package语句。不要使用jdk1.7及以上版本的特性。
主类的名字必须是:Main,否则按无效代码处理。
*/
/*
还是前面的思想 先dfs算出所有的岛屿数量用res记录 再统计不会被淹没的岛屿数目ans
二者之差即为被淹没的岛屿数
所不同的是 判断不会被淹没的判断方法发生了改变
具体是:
在某一个岛屿的搜索过程中 用全局flag标记作为该岛屿是否会不会被淹没的标志
如果存在某一块陆地相邻像素都是陆地的岛屿 那么则该岛屿不会被淹没
但是要继续遍历完该岛屿的全部陆地 使布尔数组vis对应位置标记为true
从而避免了误判
这里的flag要设置为全局变量 否则永远没有得到修改
检测是用的是局部的值false
boolean flag=false;
dfs(i,j,map,flag);
if(flag) {
ans++;
}
然而着并不能通过全部数据 最后一组数据当数据量为1000*1000时 栈溢出了
这是因为递归允许调用的最大层数为10000 在这个数据里显然超过了
因此递归搜索解决是不可能获得全部分数的
拿网上题解去跑好像没有一个是可以通过全部数据的 有更好解法欢迎评论区留言
*/
package 第九届;
import java.io.File;
import java.io.FileInputStream;
import java.io.FileNotFoundException;
import java.util.Scanner;
/**
* @author JohnnyLin
* @version Creation Time:2020年5月30日 下午5:32:40
*/
public class t09_全球变暖_优化 {
static int N;
static char map[][];
static char mapbefore[][];
static boolean flag=false;
static boolean vis[][];
//上左下右
static int dir[][]={{-1,0},{0,-1},{1,0},{0,1}};
//判断连通块数目
static void dfs(int x,int y,char[][] a) {
//dfs出口当所有陆地都被标记了
if(check(x,y)) {//找到一块陆地四周都是陆地的则将标记f设为true
//但还不能直接return 要将该岛屿遍历遍历vis对应位置标为true
flag=true;
}
for(int i=0;i<4;i++) {
int nx=x+dir[i][0];
int ny=y+dir[i][1];
if(!vis[nx][ny]&&nx>=0&&nx<N&&ny>=0&&ny<N&&a[nx][ny]=='#') {
//注意不用回溯再标记为false
vis[nx][ny]=true;
dfs(nx,ny,a);
}
}
}
//判断连通块数目
static void dfs_islandNum(int x,int y,char[][] a) {
//dfs出口为全部像素都是'.'时
for(int i=0;i<4;i++) {
int nx=x+dir[i][0];
int ny=y+dir[i][1];
if(nx>=0&&nx<N&&ny>=0&&ny<N&&a[nx][ny]=='#') {
a[nx][ny]='.';
dfs_islandNum(nx,ny,a);
}
}
}
//判断某一块陆地相邻像素是否都是陆地
private static boolean check(int x, int y) {
for(int i=0;i<4;i++) {
int nx=x+dir[i][0];
int ny=y+dir[i][1];
if(nx>=0&&nx<N&&ny>=0&&ny<N) {
if(map[nx][ny]=='.') {//相邻像素是海洋 会被淹没
return false;
}
}
}
return true;
}
static void show(char [][]a) {
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
System.out.print(a[i][j]);
}
System.out.println();
}
}
static void show2(boolean [][]a) {
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
System.out.print(String.format("%5s ", a[i][j]));
}
System.out.println();
}
}
public static void main(String[] args) throws FileNotFoundException {
//测试样例
System.setIn(new FileInputStream(new File("src/data/in7.txt") ) );
Scanner reader=new Scanner(System.in);
N=reader.nextInt();
//mapbefore=new char[N][N];
map=new char[N][N];
vis=new boolean[N][N];
mapbefore=new char[N][N];
for (int i = 0; i < N; i++) {
String s=reader.next();
for (int j = 0; j < N; j++) {
map[i][j]=s.charAt(j);
mapbefore[i][j]=map[i][j];
}
}
int res=0;
//统计先前海域的连通块数目即所有的岛屿
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
if(mapbefore[i][j]=='#') {
dfs_islandNum(i,j,mapbefore);
res++;
}
}
}
//System.out.println(res);
int ans=0;
//统计未来海域的连通块数目即未被淹没的岛屿
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
if(map[i][j]=='#'&&!vis[i][j]) {
dfs(i,j,map);
if(flag) {
ans++;
}
//将标记重新标回false 这一步很关键
flag=false;
}
}
}
//show2(vis);
//System.out.println(ans);
System.out.println(res-ans);
}
}
堆的计数
标题:堆的计数
我们知道包含N个元素的堆可以看成是一棵包含N个节点的完全二叉树。
每个节点有一个权值。对于小根堆来说,父节点的权值一定小于其子节点的权值。
假设N个节点的权值分别是1~N,你能求出一共有多少种不同的小根堆吗?
例如对于N=4有如下3种:
1
/ \
2 3
/
4
1
/ \
3 2
/
4
1
/ \
2 4
/
3
由于数量可能超过整型范围,你只需要输出结果除以1000000009的余数。
【输入格式】
一个整数N。
对于40%的数据,1 <= N <= 1000
对于70%的数据,1 <= N <= 10000
对于100%的数据,1 <= N <= 100000
【输出格式】
一个整数表示答案。
【输入样例】
4
【输出样例】
3
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
不要使用package语句。不要使用jdk1.7及以上版本的特性。
主类的名字必须是:Main,否则按无效代码处理。
/*
*利用小根堆性质 递归算法解决
在1~N范围 小根堆的根是1~N范围的最小值1
为左子树选根 假设有l种 为右子树选根 假设有r种
以1为根派生出左右子树 再在剩下N-1个数字中选择没有被选过的
且大于根的数字作为新子树的根 这是一个递归建立小根堆的过程
实质上为左右子树选根的过程就相当于给左子树划分集合的过程
假设为左子树选定lsize个结点 则右结点数也确定下来了
总的选根方案数为 :N-1选lisze的组合数 即C(N-1,lisze)
则总的堆的个数为:d(1)=C(N-1,lsize)*d(l)*d(r)
其中d(i)表示以编号为i的结点为根的堆的方案数
1、确定N-1和l、r
目标式子的递推式:
d(x)=C(size(x)-1,size(2*x))*d(2*x)*d(2*x+1)
其中size(i)表示根节点是编号为i的结点的树的结点总数目
例如N=5时
d(1)=C(4,3)*d(2)*d(3)
d(2)=C(2,1)*d(4)*d(5)
叶子节点的堆的方案数为1
d(3)=C(1,1)=1
d(4)=d(5)=1
所以总的方案数:d(1)=4*2=8
2、求组合数C(N,lsize)
c(N,lsize)=N!/(N-lsize)!/ lsize!
对阶乘进行预处理
在求阶乘过程已经对上式子求余过
对于组合数最终仍需要求余
除法求余要根据费马小定理转化为模的逆元 这里就不展开讲了
举个例子
a/b %mod模的除法没有分配律 不等于a%mod /b%mod
而是等于a*(b关于模的逆元)
而b关于模的逆元为 a^(mod-2)
求幂过程使用快速幂
所以c(N,lsize)=N!* quicikPow( (N-lsize)!,mod-2 ) * quickPow(lsize!,mod-2)
*/
package 第九届;
import java.util.Scanner;
/**
* @author JohnnyLin
* @version Creation Time:2020年6月1日 下午9:54:08
*/
public class t10_堆的计数2 {
static final int mod= 1000000009;
static int N;
static int[]size;//记录每个结点的size size[i]表示根节点是编号为i的结点的树的总结点数
static long[] a;//记录1~N的阶乘 a[i]表示i!
static long[] inv;//记录1~N阶乘的逆元 inv[i]表示i的逆元
public static void main(String[] args) {
Scanner reader = new Scanner(System.in);
N = reader.nextInt();
size=new int[N+1];
a=new long[N+1];
inv=new long[N+1];
initSize();
initA();
System.out.println(dp());
}
private static void initSize() {
// for(int i=N;i>=1;i--) {
// if(2*i+1<=N) {
// size[i]=size[2*i]+size[2*i+1]+1;
// }else if(2*i<=N) {
// size[i]=size[2*i+1]+1;
// }else {
// size[i]=1;
// }
// }
//可简写成如下
for(int i=N;i>=1;i--) {//
size[i] = 1 + (2*i<=N?size[2*i]:0)+(2*i+1<=N?size[2*i+1]:0);//size[i]<=n所以不用取余
}
}
private static void initA() {
a[0]=1;
inv[0]=1;//千万注意要初始化
for(int i=1;i<=N;i++) {
//求阶乘过程可能超过int 因此要先取余
a[i]=a[i-1]*i%mod;
//求i阶乘的逆元
inv[i]=quickPow(a[i],mod-2);
}
//show2(a)
}
private static long dp() {
//dp[i]表示编号为i的小根堆种数
long [] d=new long[N+1];
for(int x=N;x>=1;x--) {
if(2*x+1<=N)
d[x]=C(size[x]-1,size[2*x])*d[2*x]%mod*d[2*x+1]%mod;
else if(2*x<=N)
d[x]=C(size[x]-1,size[2*x])*d[2*x]%mod;
else
d[x]=1;
}
return d[1];
}
//计算组合数
static long C(int N,int lsize) {
//c(n,lsize)=N!* quicikPow( (N-lsize)!,mod-2 ) * quickPow(lsize!,mod-2)
return a[N]*inv[ lsize ]%mod*inv[ N-lsize ]%mod;
}
/**
* @param a
* @param y
* @return
* 快速求解x的y次方
*/
private static long quickPow(long a, int n) {
if(a==0)
return 0;
long ans=1;
long x=a;
while(n>0) {
if((n&1)==1)
ans=ans*x%mod;
n>>=1;
x=x*x%mod;
}
return ans;
}
private static void show(long[] d) {
for(int i=N;i>=1;i--) {
System.out.print(d[i]+" ");
}
System.out.println();
}
private static void show2(int[] d) {
for(int i=N;i>=1;i--) {
System.out.print(d[i]+" ");
}
System.out.println();
}
}