| 题目 | 用到知识点/算法类型 |
|---|---|
| 进制转换 | 水题 |
| 最多边数 | 数学知识全排列 有向图 |
| 单词重排 | 数学排列组合或dfs+集合判重 |
| 括号序列 | 枚举 |
| 反倍数 | 枚举 |
| 螺旋矩阵 | 模拟 |
| 摆动序列个数 | dfs 优化为记忆型dfs |
| 通电费用 | 并查集 最小生成树 |
| 最大植树面积 | dfs+剪枝 后缀和 |
进制转换
在计算机存储中,12.5MB是多少字节?
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
两次模拟题都出现了进制换算的,水题
1MB=1024KB
1KB=1024B(字节)
1B=8bit(位)
根据换算关系:
12.5*1024*1024=13107200
答案:13107200
最多边数
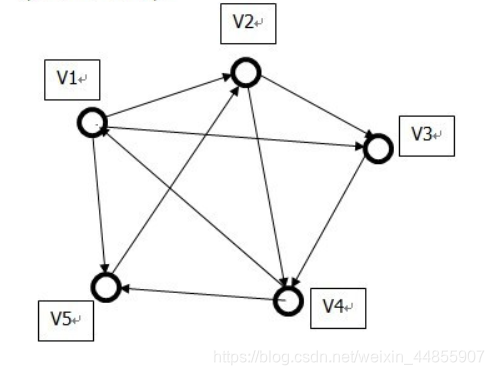
一个包含有2019个结点的有向图,最多包含多少条边?(不允许有重边)
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
所谓有向图如上图所示
每两个点组成一条边,且有方向的。
即从n中选2的全排列:A(n,2)=n*(n-1)=2019*2018=4074342
实际上 n个顶点的有向图中含有向边的数目最多为n*(n-1) 此时也叫做有向完全图
有向完全图:在有向图中,如果任意两个顶点都存在互为相反方向的两条弧,则称该图为有向完全图,含有n个顶点的有向完全图有n(n-1)条边
n个顶点的无向图中含有向边的数目最多为n*(n-1)/2
n个顶点的无向图中含有向边的数目为最少为(n-1)
单词重排
将LANQIAO中的字母重新排列,可以得到不同的单词,如LANQIAO、AAILNOQ等,注意这7个字母都要被用上,单词不一定有具体的英文意义。
请问,总共能排列如多少个不同的单词。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
思路:
当时写的时候是利用高中排列组合知识:
C(7,2) * A(5,5)=7*6/2*5*4*3*2=42*60=2520
下面代码实现,验证答案正确。
package 蓝桥杯省赛模拟题;
import java.util.HashSet;
/**
* @author JohnnyLin
* @version Creation Time:2020年6月6日 下午7:43:55
*/
public class t03_单词重排 {
static char[] a="Lanqiao".toCharArray();
static boolean vis[]=new boolean[7];//每个字母只能使用一次
static HashSet<String> set=new HashSet<String>();//单词判重 统计个数
static void dfs(int cnt,String s) {
if(cnt==7) {
set.add(s);
//System.out.println(s);
return;
}
for (int i = 0; i < 7; i++) {
if(!vis[i]) {
vis[i]=true;
dfs(cnt+1,s+a[i]);
vis[i]=false;
}
}
}
public static void main(String[] args) {
dfs(0,"");
System.out.println(set.size());
}
}
括号序列
【问题描述】
由1对括号,可以组成一种合法括号序列:()。
由2对括号,可以组成两种合法括号序列:()()、(())。
由4对括号组成的合法括号序列一共有多少种?
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
思路:
问题规模比较小 可以枚举得出来
答案:14
当规模较大时,该怎么t解呢?Leetcode上也有这道题目:22.括号生成
【题目描述】
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
【示例】
输入:n = 3
输出:[
“((()))”,
“(()())”,
“(())()”,
“()(())”,
“()()()”
]
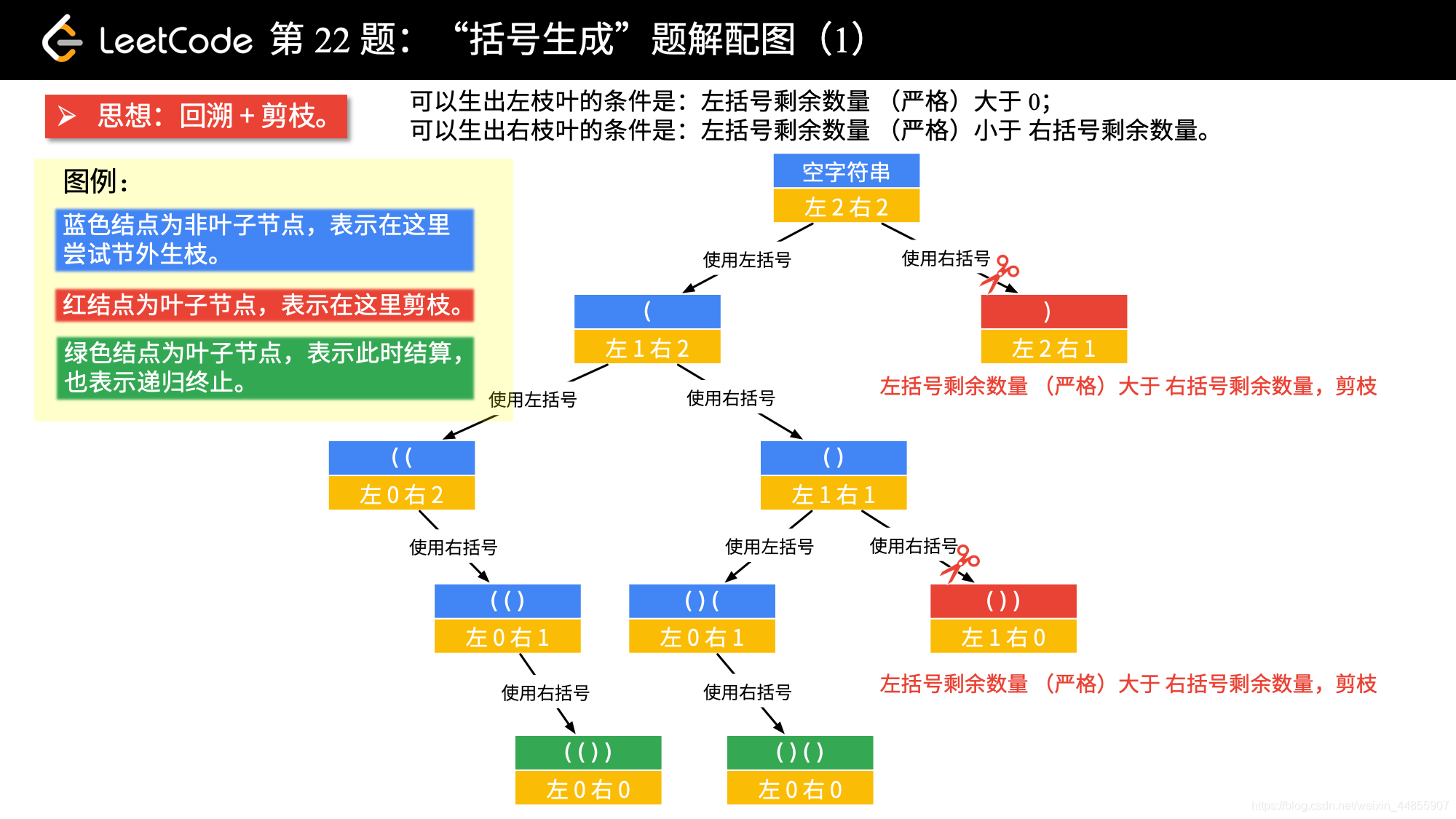
【思路】
通过观察可以发现:
1、括号组合中左括号的数量等于右括号的数量
2,括号组合中任何位置左括号的数量都是大于等于右括号的数量。
第一条显而易见,关于第二条,可以列举),不合法的括号组合:())(
第二个右括号的位置,左括号数量(数量为1)<右括号数量(数量为2)因此不合法,再看看合法的:()()、(())任何位置左括号的数目都大于等于右括号。
package DFS;
import java.util.LinkedList;
import java.util.List;
import java.util.Scanner;
/**
* @author JohnnyLin
* @version Creation Time:2020年10月8日 下午9:27:18
*/
public class _22_括号生成 {
private static int ans;
public void dfs(int leftCnt,int rightCnt,String s,List<String> res) {
if (leftCnt<0||rightCnt<0) return;
//左右括号都用完了 即得到合法解
if(leftCnt==0&&rightCnt==0) {
res.add(s);
}
//优先用左括号直至左括号用完
if(leftCnt>0)
dfs( leftCnt-1,rightCnt, s+"(",res);
//当左括号剩余的数目小于右括号才可以开始用右括号
if(leftCnt<rightCnt)
dfs( leftCnt,rightCnt-1, s+")",res);
//双分支交替进行
}
//每个位置最多有两种选择:左括号还是右括号
public List<String> generateParenthesis(int n) {
List<String> res=new LinkedList<String>();
dfs(n, n, "",res);
for (String string : res) {
System.out.println(string);
}
return res;
}
public static void main(String[] args) {
Scanner reader=new Scanner(System.in);
int n=reader.nextInt();
new _22_括号生成().generateParenthesis(n);
}
}
反倍数
5 反倍数
【问题描述】
给定三个整数 a, b, c,如果一个整数既不是 a 的整数倍也不是 b 的整数倍还不是 c 的整数倍,则这个数称为反倍数。
请问在 1 至 n 中有多少个反倍数。
【输入格式】
输入的第一行包含一个整数 n。
第二行包含三个整数 a, b, c,相邻两个数之间用一个空格分隔。
【输出格式】
输出一行包含一个整数,表示答案。
【样例输入】
30
2 3 6
【样例输出】
10
【样例说明】
以下这些数满足要求:1, 5, 7, 11, 13, 17, 19, 23, 25, 29。
【评测用例规模与约定】
对于 40% 的评测用例,1 <= n <= 10000。
对于 80% 的评测用例,1 <= n <= 100000。
对于所有评测用例,1 <= n <= 1000000,1 <= a <= n,1 <= b <= n,1 <= c <= n
package 蓝桥杯省赛模拟题;
import java.util.HashSet;
import java.util.Scanner;
import java.util.Set;
public class t06_反倍数 {
public static void main(String[] args) {
Scanner reader=new Scanner(System.in);
int n=reader.nextInt();
int a=reader.nextInt();
int b=reader.nextInt();
int c=reader.nextInt();
Set <Integer> s=new HashSet<Integer>();
for(int i=1;i<=n/a;i++) {
s.add(a*i);
}
for(int i=1;i<=n/b;i++) {
s.add(b*i);
}
for(int i=1;i<=n/c;i++) {
s.add(c*i);
}
System.out.println(n-s.size());
// for(int i=1;i<=n;i++) {
// if(!s.contains(i)) {
// System.out.print(i+" ");
// }
// }
}
}
螺旋矩阵
【问题描述】
对于一个 n 行 m 列的表格,我们可以使用螺旋的方式给表格依次填上正整数,我们称填好的表格为一个螺旋矩阵。
例如,一个 4 行 5 列的螺旋矩阵如下:
1 2 3 4 5
14 15 16 17 6
13 20 19 18 7
12 11 10 9 8
【输入格式】
输入的第一行包含两个整数 n, m,分别表示螺旋矩阵的行数和列数。
第二行包含两个整数 r, c,表示要求的行号和列号。
【输出格式】
输出一个整数,表示螺旋矩阵中第 r 行第 c 列的元素的值。
【样例输入】
4 5
2 2
【样例输出】
15
【评测用例规模与约定】
对于 30% 的评测用例,2 <= n, m <= 20。
对于 70% 的评测用例,2 <= n, m <= 100。
对于所有评测用例,2 <= n, m <= 1000,1 <= r <= n,1 <= c <= m。
思路:
关键是发现规律 找到每一个for的起始和终止点 与所处的行和列及增量step有关
画出螺旋图来就会发现规律 如上图
输入自己的测试样例:
8 5
2 2
1 2 3 4 5
22 23 24 25 6
21 36 37 26 7
20 35 38 27 8
19 34 39 28 9
18 33 40 29 10
17 32 31 30 11
16 15 14 13 12
23
package 蓝桥杯省赛模拟题;
import java.util.Scanner;
/**
* @author JohnnyLin
* @version Creation Time:2020年6月6日 下午9:52:55
*/
public class t07_螺旋矩阵2 {
static int n,m;
static void show(int a[][]) {
for (int i = 0; i <n ; i++) {
for (int j = 0; j < m; j++) {
System.out.print(a[i][j]+" ");
}
System.out.println();
}
}
public static void main(String[] args) {
Scanner reader = new Scanner(System.in);
while(reader.hasNextInt())//测试样例
{
n = reader.nextInt();
m = reader.nextInt();
int r=reader.nextInt();
int c=reader.nextInt();
int data[][]=new int[n][m];
int num=0;
int step=0;//增量是1
boolean flag=false;
while(num<n*m) {
//往右走 8 5
for (int i = 0; i < m-step*2; i++) {
if(num==n*m) {//出口条件 判断是否已经是最后一个数了
flag=true;
break;
}
num++;
data[step][i+step]=num;
}
//往下走
for (int i = step+1; i <n-step; i++) {
if(num==n*m) {
flag=true;
break;
}
num++;
data[i][m-1-step]=num;
}
//往左走
for(int i=m-2-step;i>=step;i--) {
if(num==n*m) {
flag=true;
break;
}
num++;
data[n-1-step][i]=num;
}
//往上走
for (int i = n-2-step; i >=1+step; i--) {
if(num==n*m) {
flag=true;
break;
}
num++;
data[i][step]=num;
}
step++;
}
show(data);
System.out.println(data[r-1][c-1]);
}
}
}
摆动序列
【问题描述】
如果一个序列的奇数项都比前一项大,偶数项都比前一项小,则称为一个摆动序列。即 a[2i]<a[2i-1], a[2i+1]>a[2i]。
小明想知道,长度为 m,每个数都是 1 到 n 之间的正整数的摆动序列一共有多少个。
【输入格式】
输入一行包含两个整数 m,n。
【输出格式】
输出一个整数,表示答案。答案可能很大,请输出答案除以10000的余数。
【样例输入】
3 4
【样例输出】
14
【样例说明】
以下是符合要求的摆动序列:
2 1 2
2 1 3
2 1 4
3 1 2
3 1 3
3 1 4
3 2 3
3 2 4
4 1 2
4 1 3
4 1 4
4 2 3
4 2 4
4 3 4
【评测用例规模与约定】
对于 20% 的评测用例,1 <= n, m <= 5;
对于 50% 的评测用例,1 <= n, m <= 10;
对于 80% 的评测用例,1 <= n, m <= 100;
对于所有评测用例,1 <= n, m <= 1000。
每一位可以选的范围不仅与其所处的位置(奇数位还是偶数位)有关还与其前一位所选的数相关
第1位,可选为[2,n]
选定第1位(last1),开始选第2位,可选为[1,last1-1],对所有last1结果求和
选定第2位(last2),开始选第3位,可选为[last2+1,n],对所有last2结果求和
……
package 蓝桥杯省赛模拟题;
import java.util.Scanner;
public class t08_摆动序列个数 {
static int m,n;
static int ans;
static void dfs(int begin,int end,int cnt) {
if(cnt>m) return;
if(cnt==m) {
ans=(ans+1)%10000;
return;
}
for(int i=begin;i<=end;i++) {
if((cnt+1)%2==1) {
dfs(1,i-1,cnt+1);
}else {
dfs(i+1,n,cnt+1);
}
}
}
public static void main(String[] args) {
Scanner reader=new Scanner(System.in);
m=reader.nextInt();
n=reader.nextInt();
dfs(2,n,0);
System.out.println(ans);
}
}
延续上面思路 对已经dfs搜索到的状态进行存储 置于memo数组
不过即使是这样也只能通过80%的数据 复杂度为O(n^3)
package 蓝桥杯省赛模拟题;
import java.util.Scanner;
public class t08_摆动序列个数2_记忆型dfs {
static int m,n;
static int ans;
static final int mod=10000;
//记忆型数组 m n
static int memo[][]=new int[1005][1005];
/**
* @param last 最后一个已经确定下来的数为last
* @param k 已经确定第k位
* @return
*/
static int dfs(int last,int k) {
if(k==m) {
return 1;
}
//递归前先检查历史上是否已经计算过了
if(memo[last][k]!=0) {
return memo[last][k];
}
//不存在 则计算
//该位置为偶数则数字选择范围在 [1,last-1]
if( ((k+1)&1)==0) {
for(int i=1;i<=last-1;i++) {
memo[last][k]=(memo[last][k]+dfs(i,k+1))%mod;
}
}else {//为奇数则数字选择范围在 [last+1,n]
for(int i=last+1;i<=n;i++) {
memo[last][k]=(memo[last][k]+dfs(i,k+1))%mod;
}
}
return memo[last][k];
}
public static void main(String[] args) {
Scanner reader=new Scanner(System.in);
m=reader.nextInt();
n=reader.nextInt();
for (int i = 2; i <= n; i++) {
ans=(ans+dfs(i,1))%mod;
}
System.out.println(ans);
}
}
进一步优化
在前面记忆型dfs中dfs(2,1)的含义是第1为选择2的序列数
对于在递归中求总的递归式 往往可以把递归式变成汇总或者是集合的概念
可以将递归式的参数k变成具有集合意义的
dfs(2,1)含义为序列的第1位选大于等于2的序列个数
这样就省去了外层的 加总第一位选2到n的 for循环 复杂度降为O(n^2)
dfs(last,k)可表示为
1、当k为奇数时,dfs(last,k)表示第k位选 [last,n]所有方案数之和
2、当k为偶数时,dfs(last,k)表示第k位选[1,last]所有方案数之和
*
递推式具有集合意义后 往往可以拆成 一个元素+一个少了该元素的集合(不断缩小集合范围)
就可以写成
dfs(last,k)=dfs(last-1,k+1)+dfs(las+1,k) (k为奇数时)
其中那个小元素是dfs(last+1,k) 表示第k位选定last时的方案数
(因为第k位确定了 k+1位为偶数 所以方案数为 dfs(last-1,k+1))
dfs(las+1,k)为剔除掉那个元素的集合
以此类推:
dfs(last,k)=dfs(last+1,k+1)+dfs(last-1,k) |k为偶数时
package 蓝桥杯省赛模拟题;
import java.util.Scanner;
/**
* @author JohnnyLin
* @version Creation Time:2020年6月7日 下午7:27:45
*
*/
public class t08_摆动序列个数3_优化 {
static int m,n;
static int[][] memo=new int[1005][1005];
private static final int mod=10000;
static int dfs(int last,int k) {
if (last < 1 || last > n)
return 0;
if(k==m) {
//奇数
if((k&1)==1) {
memo[last][k]=n-last+1;
}else {
memo[last][k]=last;
}
return memo[last][k];
}
if(memo[last][k]!=0) {
return memo[last][k];
}
//奇数 dfs(last,k)=dfs(last-1,k+1)+dfs(las+1,k)
if((k&1)==1) {
memo[last][k]=(dfs(last-1,k+1)+dfs(last+1,k))%mod;
}else {
//偶数 dfs(last,k)=dfs(last+1,k+1)+dfs(last-1,k)
memo[last][k]=(dfs(last+1,k+1)+dfs(last-1,k))%mod ;
}
return memo[last][k];
}
public static void main(String[] args) {
Scanner reader = new Scanner(System.in);
m = reader.nextInt();
n = reader.nextInt();
System.out.println(dfs(2, 1));
}
}
模拟赛的时候做完上面那道题时间就到了,因为那天家里做馄饨,开饭晚了,实际上只有3个小时不到的时间做。所以后面两道题都没做。
先留个坑,这两天补上。
6.10更新
哈哈哈~~ 我回来了 把坑填上
通电费用
【问题描述】
2015年,全中国实现了户户通电。作为一名电力建设者,小明正在帮助一带一路上的国家通电。
这一次,小明要帮助 n 个村庄通电,其中 1 号村庄正好可以建立一个发电站,所发的电足够所有村庄使用。
现在,这 n 个村庄之间都没有电线相连,小明主要要做的是架设电线连接这些村庄,
使得所有村庄都直接或间接的与发电站相通。小明测量了所有村庄的位置(坐标)和高度,
如果要连接两个村庄,小明需要花费两个村庄之间的坐标距离加上高度差的平方,
形式化描述为坐标为 (x_1, y_1) 高度为 h_1 的村庄与坐标为 (x_2, y_2) 高度为 h_2 的村庄之间连接的费用为
sqrt((x_1-x_2)*(x_1-x_2)+(y_1-y_2)*(y_1-y_2))+(h_1-h_2)*(h_1-h_2)。
在上式中 sqrt 表示取括号内的平方根。请注意括号的位置,高度的计算方式与横纵坐标的计算方式不同。
由于经费有限,请帮助小明计算他至少要花费多少费用才能使这 n 个村庄都通电。
【输入格式】
输入的第一行包含一个整数 n ,表示村庄的数量。
接下来 n 行,每个三个整数 x, y, h,分别表示一个村庄的横、纵坐标和高度,其中第一个村庄可以建立发电站。
【输出格式】
输出一行,包含一个实数,四舍五入保留 2 位小数,表示答案。
【样例输入】
4
1 1 3
9 9 7
8 8 6
4 5 4
【样例输出】
17.41
【评测用例规模与约定】
对于 30% 的评测用例,1 <= n <= 10;
对于 60% 的评测用例,1 <= n <= 100;
对于所有评测用例,1 <= n <= 1000,0 <= x, y, h <= 10000。
思路
路线建设费用最少 离散数学里的最小生成树问题
每个村庄对应图的一个顶点 每两个村庄之间电线相连的费用对应图的权值
要使费用之和最少即权值之和最少 为最小生成树问题用克鲁斯卡尔最小生成树法
package 蓝桥杯省赛模拟题;
import java.util.ArrayList;
import java.util.Collections;
import java.util.HashMap;
import java.util.HashSet;
import java.util.List;
import java.util.Map;
import java.util.Scanner;
import java.util.Set;
/**
* @author JohnnyLin
* @version Creation Time:2020年6月8日 下午10:59:18
*/
public class t09_通电费用 {
static Point c[];
static Map map=new HashMap<>();
public static void main(String[] args) {
Scanner reader=new Scanner(System.in);
int n=reader.nextInt();
//n个村庄
c=new Point[n];
for (int i = 0; i < n; i++) {
c[i]=new Point();
c[i].x=reader.nextInt();
c[i].y=reader.nextInt();
c[i].h=reader.nextInt();
}
//构建所有边
List <Edge>edgeList=new ArrayList<Edge>(n*n);
for(int i=0;i<n-1;i++) {
for(int j=i+1;j<n;j++) {
edgeList.add(new Edge(i,j));
}
}
//升序排序 sort 方法只能对一维的数据结构(一维数组 列表)进行排序
Collections.sort(edgeList);
//根据已有的边及其权重生成最小生成树
int cnt=0;
double ans=0;
for(Edge e:edgeList) {
if(!check(e)) {
continue;
}
//该边加入后不会破坏树的性质 加入到最小生成树中
cnt++;
ans+=e.cost;
//最小生成树已经全部构建好了
if(cnt==n-1) {
//注意四舍五入 精度转换问题除以100.0而不是100
ans=Math.round(ans*100)/100.0;
System.out.println(String.format("%.2f", ans));
return;
}
}
}
//并查集中查询e的起点和终点是否在一个集中
private static boolean check(Edge e) {
UFNode x=UnionFind.find(e.i);
UFNode y=UnionFind.find(e.j);
//System.out.println(e.i.parent+" "+e.j.parent);
if(x!=y) {//掌门人属于不同集合 以这两个点为顶点边的可加
UnionFind.Union(e.i, e.j);
//System.out.println(e.i.parent+" "+e.j.parent);
return true;
}
return false;
}
//Point类保存每个村庄的横、纵坐标和高度信息
private static class Point{
int x,y,h;
}
private static class Edge implements Comparable<Edge>{
//第i个村庄与第j个村庄构成的边
UFNode i,j;
double cost;
public Edge(int i,int j) {
double a=Math.sqrt((c[i].x-c[j].x)*(c[i].x-c[j].x)+(c[i].y-c[j].y)*(c[i].y-c[j].y));
this.cost=a+(c[i].h-c[j].h)*(c[i].h-c[j].h);
//System.out.println(cost);
this.i=new UFNode();
this.j=new UFNode();
}
public int compareTo(Edge o) {
return (int) (this.cost-o.cost);
}
}
//并查集
static class UnionFind{
static UFNode find(UFNode x) {
UFNode p=x;
Set<UFNode> set=new HashSet<UFNode>();
//逐层往上找 一直找到它的掌门人
//注意此处是p.parent 不是p
while(p.parent!=null) {
set.add(p);
p=p.parent;
}
//掌门人就是p 将全部小弟的parent修改为p归于p门下
for (UFNode son : set) {
son.parent=p;
}
return p;
}
/**
* @param x
* @param y
* 将y归并到x所属集合中
*/
public static void Union(UFNode x,UFNode y){
find(y).parent=x;
}
}
static class UFNode{
UFNode parent;
}
}
植树覆盖面积
【问题描述】
小明和朋友们一起去郊外植树,他们带了一些在自己实验室精心研究出的小树苗。
小明和朋友们一共有 n 个人,他们经过精心挑选,在一块空地上每个人挑选了一个适合植树的位置,总共 n 个。他们准备把自己带的树苗都植下去。
然而,他们遇到了一个困难:有的树苗比较大,而有的位置挨太近,导致两棵树植下去后会撞在一起。
他们将树看成一个圆,圆心在他们找的位置上。如果两棵树对应的圆相交,这两棵树就不适合同时植下(相切不受影响),称为两棵树冲突。
小明和朋友们决定先合计合计,只将其中的一部分树植下去,保证没有互相冲突的树。他们同时希望这些树所能覆盖的面积和(圆面积和)最大。
【输入格式】
输入的第一行包含一个整数 n ,表示人数,即准备植树的位置数。
接下来 n 行,每行三个整数 x, y, r,表示一棵树在空地上的横、纵坐标和半径。
【输出格式】
输出一行包含一个整数,表示在不冲突下可以植树的面积和。由于每棵树的面积都是圆周率的整数倍,请输出答案除以圆周率后的值(应当是一个整数)。
【样例输入】
6
1 1 2
1 4 2
1 7 2
4 1 2
4 4 2
4 7 2
【样例输出】
12
【评测用例规模与约定】
对于 30% 的评测用例,1 <= n <= 10;
对于 60% 的评测用例,1 <= n <= 20;
对于所有评测用例,1 <= n <= 30,0 <= x, y <= 1000,1 <= r <= 1000。
思路
就是在n个坑(坑跟树是捆绑在一起的)中选k(k<=n)个坑 使得满足题意(任意两棵树的不相交)的条件下 圆的面积和最大
由于不知道选多少个坑(k=1 、2、3……n)的时候 圆的面积最大 因此要算出每一个k的最大圆面积和 再求一个最大值
任意两棵树的不相交的状态怎么表示呢? 临界状态是相切
高中数学学过 两个圆的圆心距离大于等于半径和即为不相交状态 因此要有一个数组vis标记已经选过的坑
默认每个坑的位置都是不一样的 不会由两个一样位置的坑
这种复杂度很高 O(n*2^n*N*N) 每次check都是最大规模N的检查
package 蓝桥杯省赛模拟题;
import java.util.Scanner;
/**
* @author JohnnyLin
* @version Creation Time:2020年6月9日 下午8:24:54
*/
public class t10_最大植树面积 {
static final int N=1005;
static int ans,n;
static int a[][];
static boolean vis[][]=new boolean[N][N];
//r[i][j]存储(i,j)位置坑的树的半径
static int r[][]=new int [N][N];
/**
* @param index 当前选了哪个坑的树
* @param cnt 当前还剩多个坑要选
* @param sum 当前选的树的面积和
* @return
*/
static void dfs(int index,int cnt,int sum) {
if(cnt==0) {
if(ans<sum) {
ans=sum;
}
return ;
}
for(int i=0;i<n;i++) {
int x=a[i][0];
int y=a[i][1];
if(!vis[x][y]&&check(i)) {
vis[x][y]=true;
dfs(i,cnt-1,sum+a[i][2]*a[i][2]);
vis[x][y]=false;
}
}
}
private static boolean check(int index) {
for (int i = 1; i <=1000; i++) {
for (int j = 1; j <=1000; j++) {
if(vis[i][j]) {
if((i-a[index][0])*(i-a[index][0])+(j-a[index][1])*(j-a[index][1])
<(a[index][2]+r[i][j])*(a[index][2]+r[i][j]) ) {
return false;
}
}
}
}
return true;
}
public static void main(String[] args) {
Scanner reader=new Scanner(System.in);
n=reader.nextInt();
a=new int[n][3];
//注意 由于n是static的(初始值为0) 所以如果把new r数组置于全局变量位置
//程序一启动r就被new出来 得到的长度将是一行一列
for (int i = 0; i <n; i++) {
for (int j = 0; j < 3; j++) {
a[i][j]=reader.nextInt();
}
r[a[i][0]][a[i][1]]=a[i][2];
}
for (int i = 1; i <=n; i++) {
dfs(0,i,0);
}
System.out.println(ans);
}
}
* 将圆按半径从大到小排序,优先选择半径大的
* 因为 理论上这样半径大的
* 用数组s存储所有圆的半径的平方的后缀和
* dfs函数中 参数sum表示index之前的选择策略得到的sum
* s[index]表示index及之后所有圆的半径平方和
* 如果sum+s[index]小于等于历史上的ans 可直接return退出当前分支的递归 尝试下一个index
package 蓝桥杯省赛模拟题;
import java.util.Arrays;
import java.util.Scanner;
/**
* @author JohnnyLin
* @version Creation Time:2020年6月9日 下午10:30:49
*/
public class t10_最大植树面积_优化 {
static Scanner reader=new Scanner(System.in);
static int n,ans;
static Tree []trees;
//半径平方后缀和
static int[] suffix;
//邻接矩阵 保存每两棵树是否冲突
static int [][]adjaTable;
private static void dfs(int index, int sum) {
if(index==n) {
ans=Math.max(sum, ans);
return;
}
//不更新 剪枝
if(suffix[index]+sum<=ans) {
return;
}
//不冲突则选
if(ok(index)) {
trees[index].selected=true;
//选择索引为index的树 sum+trees[index].rr
dfs(index+1,sum+trees[index].rr);
trees[index].selected=false;
}
trees[index].selected=false;
dfs(index+1,sum);
}
private static boolean ok(int index) {
for(int i=0;i<n;i++) {
//如果已经选了的树和现在要选的索引为index的树冲突 那么这棵树树不能选
if(trees[i].selected&&adjaTable[i][index]==1) {
return false;
}
}
return true;
}
public static void main(String[] args) {
n = reader.nextInt();
initTrees();
initSuffix();
initAdjaTable();
dfs(0, 0);
System.out.println(ans);
}
private static void initAdjaTable() {
adjaTable=new int[n][n];
//对称关系
for (int i = 0; i < n-1; i++) {
for (int j = i+1; j < n; j++) {
//相交
if(Tree.intersected(trees[i],trees[j])) {
adjaTable[i][j]=1;
adjaTable[j][i]=1;
}
}
}
}
private static void initSuffix() {
suffix=new int[n];
for (int i = n-2; i>=0;i--) {
suffix[i]=suffix[i+1]+trees[i].rr;
}
}
private static void initTrees() {
trees=new Tree[n];
for(int i=0;i<n;i++) {
trees[i]=new Tree(reader.nextInt(),reader.nextInt(),reader.nextInt());
}
//从小到大排序
Arrays.sort(trees);
}
static class Tree implements Comparable<Tree>{
//rr 圆的半径平方
int x,y,r,rr;
//是否已经被选中
boolean selected;
Tree(int x,int y, int r){
this.x=x;
this.y=y;
this.r=r;
this.rr=r*r;
}
//判断两棵树有没有冲突
public static boolean intersected(Tree a,Tree b) {
return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)<(a.r+b.r)*(a.r+b.r);
}
@Override
public int compareTo(Tree o) {
return this.r-o.r;
}
}
}