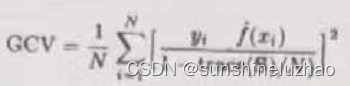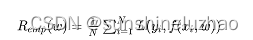对于平方误差下的线性拟合，广义交叉验证提供了一种对留一交叉验方便的逼近，线性拟合的方法可以写成
![在这里插入图片描述](https://img-blog.csdnimg.cn/direct/63f8b5131faa469383adba0424e05f3f.png
对于许多线性拟合


在这里可以把S理解成帽子矩阵，则GCV可以看成是留一交叉验证的估计。
在岭回归中，也可以类似的写出GCV的逼近公式，对于整个训练集来说，交叉验证是有偏估计，拿出一部分训练的估计是无偏估计。总的来说，GCV是test error 的一个无偏估计。

几个容易混淆的概念：
1.训练误差：模型在训练集上的误差。
2.泛化误差：模型在新样本上的误差，通常将测试误差作为泛化误差的估计。
3.经验风险：模型在整个训练集上的误差的均值。

4.期望风险：模型在所有可能出现的样本上的误差的均值。
期望风险的上界

5.结构风险

最小化结构风险，等价于最小化模型的参数，也就是模型参数的正则化。