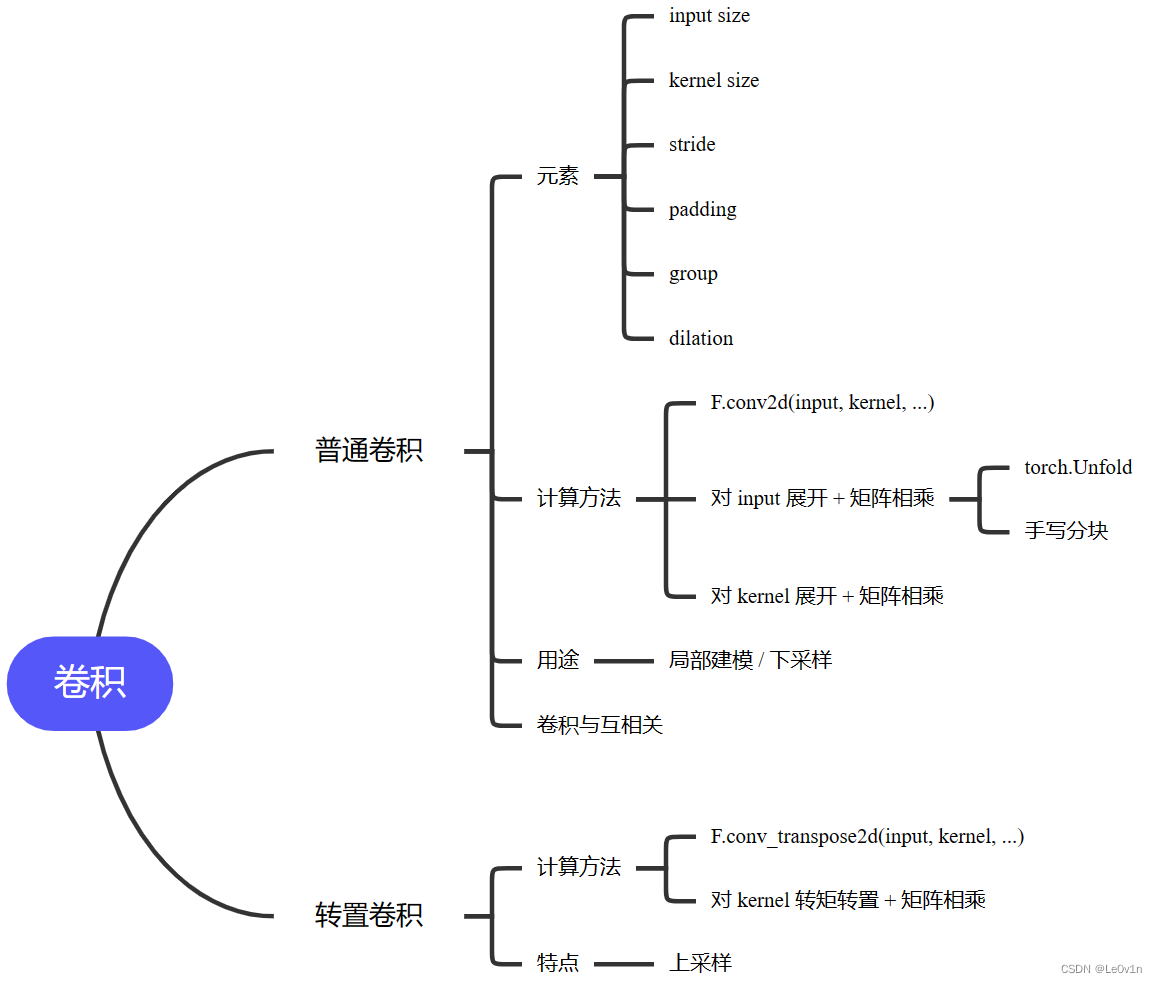
0. 学习路线
本文讲解普通卷积。
1. PyTorch 中卷积的分类
在 PyTorch 中,普通卷积一般有三种:
nn.conv1d():用于一维信号(例如时间序列数据)的卷积层。nn.conv2d():用于二维图像的卷积层,常用于处理图像数据。nn.conv3d():用于三维数据(例如视频数据或三维扫描数据)的卷积层。
这里我们主要讲解 nn.conv2d,因为 nn.conv1d 和 nn.conv3d 可以当做 nn.conv2d 那样去计算。
2. nn.Conv2d 和 nn.conv2d 的区别
我们在搜索 conv2d 时会发现有两种:
Conv2dconv2d
二者的字母 C 一个是大写的一个是小写的,那么二者有区别吗?答案是肯定的,具体区别如下:
Conv2d:是用于构造卷积层的类(Class),用于创建卷积层对象。conv2d:是一个函数(function),用于执行卷积操作,它直接进行卷积计算。
注意❗️:二者除了本质上有区别外,还存在一些值得我们关注的差异:
Conv2d是用于构造卷积层的类(Class),用于创建卷积层对象。这是一个模型组件,它具有可学习的参数(如权重和偏置),并且在模型训练过程中会通过反向传播更新这些参数。conv2d:因为这个卷积是一个函数(function),用于执行卷积操作,它直接进行卷积计算。这个函数没有可学习的参数,因此在模型训练过程中不能通过反向传播来调整它的参数。
由于
Conv2d是一个卷积层的类,而且可以自动管理权重和偏置的学习过程,通常情况下,我们在构建深度学习模型时会使用nn.Conv2d而不是nn.conv2d。在定义模型结构时,Conv2d通常作为卷积层的组件使用,而在模型的前向传播过程中,我们会使用conv2d函数来执行具体的卷积操作。这样,Conv2d和conv2d可以协同工作,形成完整的深度学习模型。
3. torch.nn.Conv2d
CLASStorch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0,
dilation=1, groups=1, bias=True, padding_mode='zeros',
device=None, dtype=None)
以上是 PyTorch 中 torch.nn.Conv2d 类的构造函数( __init__ 方法),目的用于创建一个二维卷积层。
PyTorch 官方 API 地址:https://pytorch.org/docs/1.12/generated/torch.nn.Conv2d.html?highlight=conv2d#torch.nn.Conv2d
参数说明如下:
-
in_channels(int):输入图像的通道数。对于彩色图像,通常为 3(RGB),对于灰度图像,通常为 1。 -
out_channels(int):输出通道数,也就是卷积核的数量,每个卷积核会生成一个输出通道。也就是卷积操作后生成的特征图数量。 -
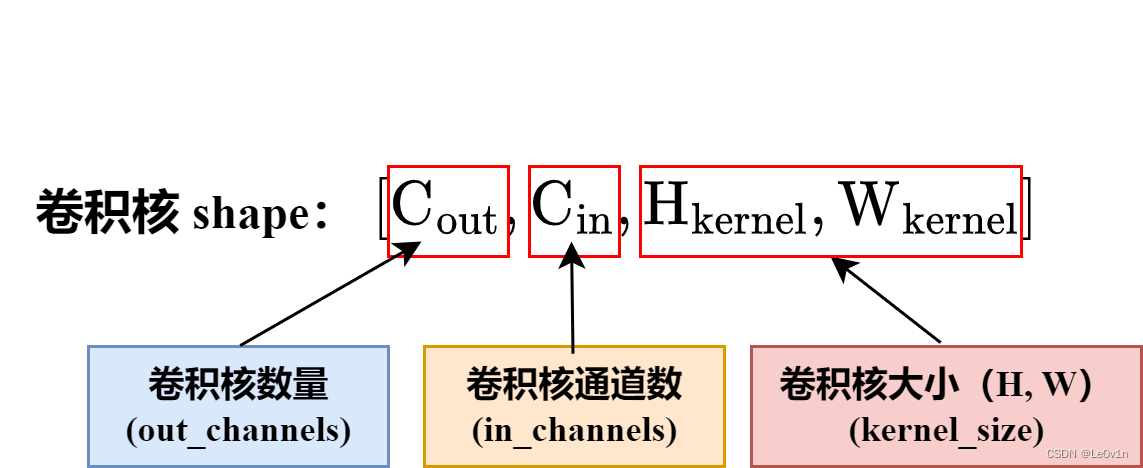
kernel_size(int 或 tuple):卷积核的大小。如果是 int 类型,表示卷积核的高度和宽度相等;如果是 tuple 类型,如kernel_size=(3, 5),表示卷积核的高度和宽度分别为 3 和 5。 -
stride(int 或 tuple,可选):卷积操作的步长(stride)。如果是 int 类型,表示在高度和宽度方向上的步长相等;如果是 tuple 类型,如stride=(2, 1),表示在高度和宽度方向上的步长分别为 2 和1。默认值为 1。 -
padding(int 或 tuple,可选):在 输入图像的周围 添加零值填充(padding)的层数。如果是 int 类型,表示在高度和宽度方向上的填充层数相等;如果是 tuple 类型,如 (1, 2),表示在高度和宽度方向上的填充层数分别为 1 和 2。默认值为 0。 —— 使用什么填充需要看padding_mode -
dilation(int 或 tuple,可选):控制卷积核内部元素之间的间距(dilation)。如果是 int 类型,表示在卷积核内部元素之间的间距在高度和宽度方向上相等;如果是 tuple 类型,如 (2, 2),表示在高度和宽度方向上的间距分别为 2。默认值为 1(不使用膨胀卷积)。 -
groups(int,可选):控制输入和输出通道之间的连接方式。当 groups>1 时,表示使用分组卷积,将输入通道和输出通道分成 groups 组,并分别进行卷积操作。默认值为 1,即普通卷积。 -
bias(bool,可选):是否添加偏置项。如果为 True,表示会为每个输出通道添加 一个 偏置项;如果为 False,表示不添加偏置项。默认值为 True。 -
padding_mode(str,可选):选择 padding 的模式。可选值为 ‘zeros’(默认值)或 ‘reflect’。- ‘zeros’ 表示使用 0 进行填充
- ‘reflect’ 表示使用输入图像的边界值进行填充
-
device(torch.device,可选):指定该层运行在哪个设备上(例如 CPU 或 GPU)。默认值为 None,表示使用默认设备。 -
dtype(torch.dtype,可选):指定该层的数据类型。默认值为 None,表示使用默认数据类型。
3.1 卷积过程示意图
以上其实是 nn.conv1d 的卷积过程,nn.conv2d 本质上是一样的。
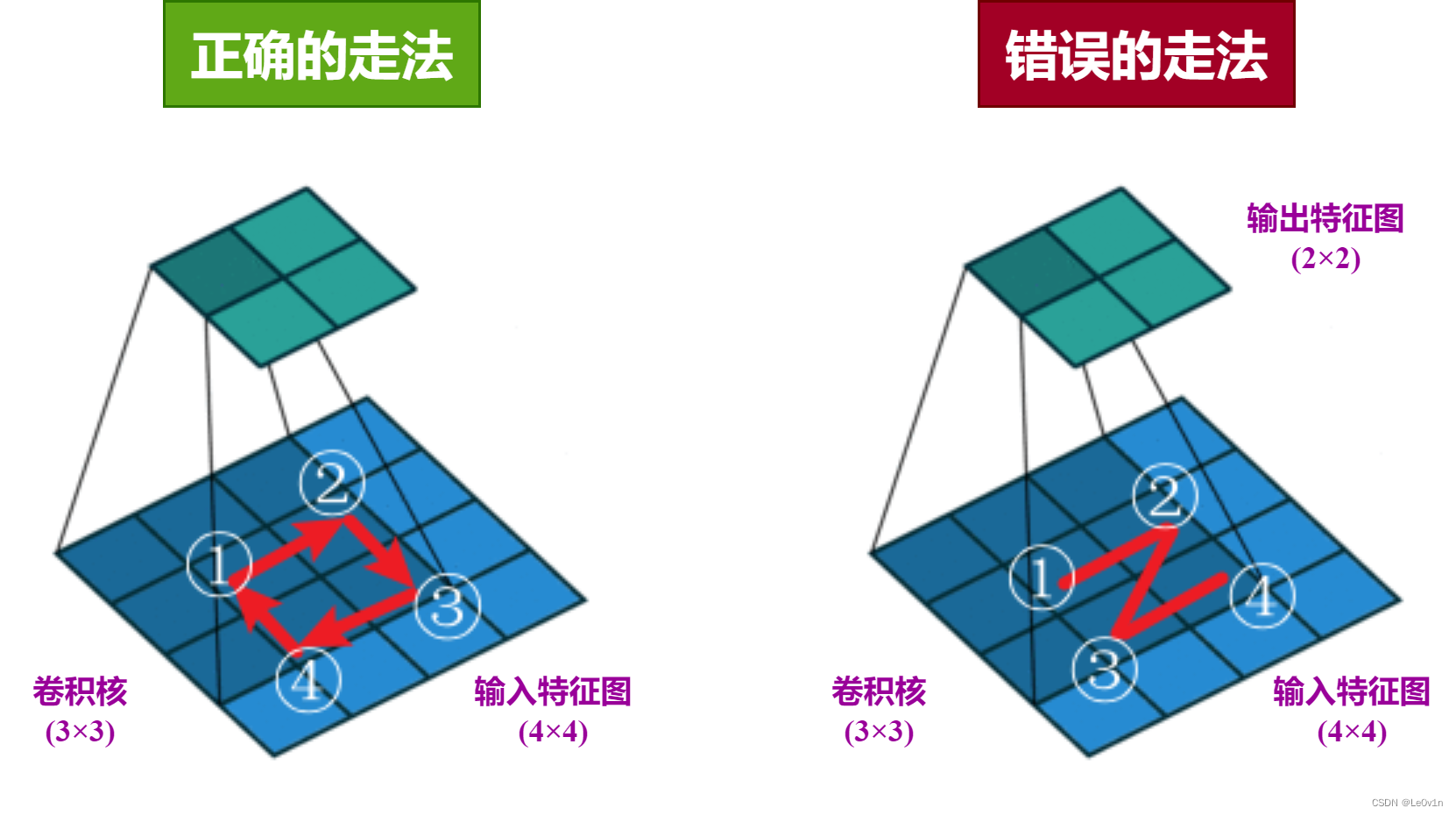
值得注意的是❗️:
- 在卷积操作中,卷积核的滑动方式是走 回字形轨迹 而不是 Z 型轨迹(这里的 gif 动图是有问题的,它走的是 Z 型轨迹)。
确切来说是一个 “弓” 字型轨迹。
- 上面是没有偏置的,如果有偏置,也不影响图片,只不过输出特征图会沿着通道方向加上一个偏置(输出特征图一共会加
out_channels个偏置)。
偏置项的作用是为了引入对输入数据的线性偏移,使模型能够更好地拟合数据。在卷积层中,对于每个输出通道,都有一个对应的偏置项。在进行卷积操作时,每个输出通道的卷积结果会与相应的偏置项 相加,从而得到输出特征图。
在模型训练过程中,nn.Conv2d 会不断通过反向传播更新自己的参数,即 ①卷积核参数和 ②偏置项:
-
卷积核参数(Weights):每个卷积核都是一个可学习的参数矩阵,用于在输入图像上执行特征提取。
nn.Conv2d层会学习这些卷积核的参数,使得它们能够有效地捕捉输入图像中的不同特征。 -
偏置项(Bias):如果在
nn.Conv2d中使用了偏置(bias=True),那么每个输出通道都会有一个可学习的偏置项。这些偏置项用于引入对输入数据的线性偏移,使得模型能够更好地拟合数据。
❗️❗️我们一定不要搞错,特征图参数不是我们所考虑的内容,更新参数一定是更新卷积的参数,即卷积核参数和偏置项。
3.2 卷积代码示例
import torch
import torch.nn as nn
import torch.nn.functional as F
# 实例化一个二维卷积
conv_layer = torch.nn.Conv2d(in_channels=1, out_channels=1, kernel_size=(3, 3),
stride=1, padding=0, bias=False)
# 定义一个输入特征图
input_feature_map = torch.randn(size=[1, 1, 4, 4]) # BS, C, H, W
# 将输入特征图送入卷积得到输出特征图
output_feature_map = conv_layer(input_feature_map)
print(f"----------------输入特征图--------------------")
print(f"input feature map: {input_feature_map}")
print(f"input feature map.shape: {input_feature_map.shape}")
"""
input feature map: tensor([[[[ 1.3073, -1.5880, -0.9452, 0.4990],
[ 0.4691, -0.0185, 1.7039, 0.4509],
[ 1.0158, 1.7649, -1.1296, 0.0249],
[ 1.7177, -1.5447, 0.0709, 1.0709]]]])
input feature map.shape: torch.Size([1, 1, 4, 4])
"""
print(f"\r\n----------------输出特征图--------------------")
print(f"output feature map: {output_feature_map}")
print(f"output feature map.shape: {output_feature_map.shape}")
print(f"output feature map.shape: {output_feature_map.shape}")
print(f"output feature map.dtype: {output_feature_map.dtype}")
print(f"output feature map.device: {output_feature_map.device}")
print(f"output feature map.size(): {output_feature_map.size()}")
print(f"output feature map.dim(): {output_feature_map.dim()}")
print(f"output feature map.ndim: {output_feature_map.ndim}")
print(f"output feature map.numel(): {output_feature_map.numel()}")
"""
output feature map: tensor([[[[ 1.5613, -0.6933],
[-1.4673, -0.6003]]]], grad_fn=<ConvolutionBackward0>)
output feature map.shape: torch.Size([1, 1, 2, 2])
output feature map.shape: torch.Size([1, 1, 2, 2])
output feature map.dtype: torch.float32
output feature map.device: cpu
output feature map.size(): torch.Size([1, 1, 2, 2])
output feature map.dim(): 4
output feature map.ndim: 4
output feature map.numel(): 4
"""
print(f"\r\n----------------卷积层--------------------")
print(f"conv_layer.in_channels: {conv_layer.in_channels}")
print(f"conv_layer.out_channels: {conv_layer.out_channels}")
print(f"conv_layer.kernel_size: {conv_layer.kernel_size}")
print(f"conv_layer.stride: {conv_layer.stride}")
print(f"conv_layer.padding: {conv_layer.padding}")
print(f"conv_layer.bias: {conv_layer.bias}")
print(f"conv_layer.weight: {conv_layer.weight}")
print(f"conv_layer.weight.shape: {conv_layer.weight.shape}")
"""
conv_layer.in_channels: 1
conv_layer.out_channels: 1
conv_layer.kernel_size: (3, 3)
conv_layer.stride: (1, 1)
conv_layer.padding: (0, 0)
conv_layer.bias: None
conv_layer.weight: Parameter containing:
tensor([[[[ 0.1567, -0.0156, -0.1600],
[-0.2636, -0.2253, 0.2938],
[ 0.1223, 0.3061, -0.1196]]]], requires_grad=True)
conv_layer.weight.shape: torch.Size([1, 1, 3, 3])
"""
3.3 特征图(Feature map)可查看的属性
在PyTorch中,一个特征图(Feature Map)是一个由 torch.Tensor 表示的多维数组。我们可以使用 torch.Tensor 的属性和方法来查看特征图的相关信息。
一般来说,以下是我们可以查看的特征图的一些属性:
-
shape:使用.shape属性可以查看特征图的形状,它告诉你特征图的维度大小,如(batch_size, channels, height, width)。 -
dtype:使用.dtype属性可以查看特征图的数据类型,通常是 float32 或 float64。 -
device:使用.device属性可以查看特征图所在的设备,如 CPU 或 GPU。 -
size():使用.size()方法可以查看特征图的尺寸,它返回一个元组 tuple,包含特征图在每个维度上的大小。 -
dim():使用.dim()方法可以查看特征图的维度数量。 -
ndim:使用.ndim属性可以查看特征图的维度数量,与dim()方法功能相同。 -
numel():使用.numel()方法可以查看特征图的元素总数,即特征图中所有元素的个数。
除了这些基本属性,我们还可以通过 索引 和 切片 的操作查看特征图中的具体数值。例如,使用 tensor[0] 可以查看第一个样本(batch_size 维度)的特征图,tensor[:, 0] 可以查看第一个通道的特征图,tensor[:, :, 2:5, 3:6] 可以查看特定高度和宽度范围的子集。
在实际使用中,特征图的属性可以帮助我们了解数据的形状和类型,有助于调试和确认模型的输出。
重点记忆:
.shape、.device即可。
3.4 卷积层(Convolution)可查看的属性
对于定义的 nn.Conv2d,我们可以查看以下属性:
-
in_channels:输入通道数。 -
out_channels:输出通道数。 -
kernel_size:卷积核的大小。 -
stride:卷积操作的步长。 -
padding:填充层数。 -
dilation:卷积核元素之间的间距。 -
groups:输入和输出通道之间的连接方式。 -
bias:是否有偏置项。 -
padding_mode:填充的模式。 -
weight:卷积核的权重参数。 -
bias:偏置项的参数。
这些属性描述了卷积层的配置和参数信息,它们可以帮助我们了解和确认卷积层的设置。要查看这些属性的值,我们可以直接通过 nn.Conv2d 对象来访问它们,例如:
print(nn.conv2d.in_channels) # 输出输入通道数
print(nn.conv2d.out_channels) # 输出输出通道数
print(nn.conv2d.kernel_size) # 输出卷积核的大小
print(nn.conv2d.stride) # 输出卷积操作的步长
print(nn.conv2d.padding) # 输出填充层数
print(nn.conv2d.dilation) # 输出卷积核元素之间的间距
print(nn.conv2d.groups) # 输出输入和输出通道之间的连接方式
print(nn.conv2d.bias) # 输出是否有偏置项
print(nn.conv2d.padding_mode) # 输出填充的模式
print(nn.conv2d.weight) # 输出卷积核的权重参数
print(nn.conv2d.bias) # 输出偏置项的参数
这些属性信息是创建 nn.Conv2d 对象时指定的参数,也包含了该卷积层的权重参数和偏置项参数。
4. torch.nn.functional.conv2d
PyTorch 官方 API 地址:https://pytorch.org/docs/1.12/generated/torch.nn.functional.conv2d.html?highlight=conv2d#torch.nn.functional.conv2d
torch.nn.functional.conv2d(input, weight, bias=None, stride=1,
padding=0, dilation=1, groups=1) -> Tensor
torch.nn.functional.conv2d 是 PyTorch 中用于执行二维卷积操作的函数。它和 torch.nn.Conv2d 是两种不同的实现方式,其中 torch.nn.functional.conv2d 是一个函数,而 torch.nn.Conv2d 是一个类。 torch.nn.functional.conv2d 函数提供了更灵活的操作,可以在函数调用时直接指定卷积核的权重参数,而不需要像类那样在初始化时定义。
参数说明:
-
input:输入的特征图,一个四维张量,形状为(batch_size, in_channels, height, width)。 -
weight:卷积核的权重参数,一个四维张量,形状为(out_channels, in_channels, kernel_height, kernel_width)。 -
bias:可选的偏置项参数,一个一维张量,形状为(out_channels,)。默认值为 None,表示不使用偏置项。 -
stride:卷积操作的步长,可以是一个整数或一个元组(stride_height, stride_width)。默认值为 1。 -
padding:填充层数,可以是一个整数或一个元组(padding_height, padding_width)。默认值为 0。 -
dilation:卷积核元素之间的间距,可以是一个整数或一个元组(dilation_height, dilation_width)。默认值为 1。 -
groups:输入和输出通道之间的连接方式,控制卷积操作的分组,可以是一个整数。默认值为 1,表示普通卷积。
该函数的返回值是执行卷积操作后得到的特征图,一个四维张量,形状为 (batch_size, out_channels, output_height, output_width)。
使用torch.nn.functional.conv2d函数时,需要手动传入卷积核的权重参数。它通常在自定义模型或一些特定的卷积操作中使用,而在大多数情况下,建议使用torch.nn.Conv2d类,它更简单方便,自动管理卷积核的权重参数。
4.1 卷积过程示意图
与 torch.nn.Conv2d 没有区别。
4.2 卷积代码示例
import torch
import torch.nn as nn
import torch.nn.functional as F
# 固定随机数种子
torch.manual_seed(10010)
# 定义一个输入特征图
input_feature_map = torch.randn(size=[1, 1, 4, 4]) # BS, C, H, W
# 实例化一个二维卷积
conv_layer = torch.nn.Conv2d(in_channels=1, out_channels=1, kernel_size=(3, 3),
stride=1, padding=0, bias=False)
# 定义卷积核参数
kernel_weight = torch.Tensor([[[[-0.0765, 0.1716, 0.2779],
[-0.1685, -0.1217, 0.0160],
[0.1584, -0.2000, -0.2148]]]])
# 将输入特征图送入卷积得到输出特征图
output_feature_map_1 = conv_layer(input_feature_map)
# 直接使用卷积得到输出特征图
output_feature_map_2 = torch.nn.functional.conv2d(
input=input_feature_map, weight=kernel_weight, bias=None, stride=1, padding=0) # F.conv2d()也可以
print(f"\r\n----------------输出特征图--------------------")
print(f"output feature map 1: {output_feature_map_1}")
print(f"output feature map 2: {output_feature_map_2}")
结果:
output feature map 1: tensor([[[[ 1.3038, 0.0875],
[-0.8772, -0.1317]]]], grad_fn=<ConvolutionBackward0>)
output feature map 2: tensor([[[[ 1.3037, 0.0875],
[-0.8773, -0.1318]]]])
grad_fn=<ConvolutionBackward0> 是输出特征图在计算时生成的一个梯度函数(gradient function),它用于跟踪计算图,并在反向传播时计算梯度。这是因为 output_feature_map_1 是通过调用 conv_layer(input_feature_map) 来计算的,它是一个由 torch.nn.Conv2d 类型的对象进行操作的结果。由于 torch.nn.Conv2d 类自带梯度计算功能,因此在计算 output_feature_map_1 时,PyTorch自动在其上创建了梯度函数。
而对于 output_feature_map_2,它是通过调用 torch.nn.functional.conv2d 函数计算得到的。这是一个纯函数(pure function),它没有任何与梯度相关的操作,因此在计算 output_feature_map_2 时,并不会生成梯度函数。
当我们调用类方法或属性时,PyTorch会在这些操作上自动创建梯度函数。但是对于纯函数,由于它们不涉及可训练参数的梯度计算,所以不会生成梯度函数。
5. 卷积运算示意
卷积和池化后形状计算公式分别如下:
没有空洞卷积的计算:
H
/
W
i
c
o
n
v
/
p
o
o
l
=
H
/
W
i
i
n
+
2
p
i
−
k
i
s
i
+
1
\mathrm{H / W}_i^{\mathrm{conv / pool }}=\frac{\mathrm{H / W}_i^{\mathrm{in}}+2p_i-k_i}{s_i}+1
H/Wiconv/pool=siH/Wiin+2pi−ki+1
带有空洞卷积后的计算:
H / W i d i a l a t e d c o n v = H / W i i n + 2 p i − d i × ( k i − 1 ) s i + 1 \mathrm{H / W}_i^{\mathrm{dialated \ conv}}=\frac{\mathrm{H / W}_i^{\mathrm{in}}+2p_i-d_i\times (k_i-1)}{s_i}+1 H/Widialated conv=siH/Wiin+2pi−di×(ki−1)+1
卷积: 向下取整
池化: 向上取整
5.1 stride=1, padding=0
根据上面的公式可知,输出特征图大小为:
H / W i = H / W i i n + 2 p i − k i s i + 1 = 5 + 2 × 0 − 3 1 + 1 = 3 \begin{aligned} \mathrm{H / W}_i & = \frac{\mathrm{H / W}_i^{\mathrm{in}}+2p_i-k_i}{s_i}+1\\ & = \frac{5 + 2\times 0 - 3}{1} + 1\\ & = 3 \end{aligned} H/Wi=siH/Wiin+2pi−ki+1=15+2×0−3+1=3
即输出特征图的宽度和高度为 3 × 3 3 \times 3 3×3。
❗️注意❗️:特征图和卷积核的乘法是点乘(element-wise multiplication),也被成为逐元素乘法或内积,即对应位置元素相乘最后再求和,而非我们理解的矩阵乘法。
5.2 stride=2, padding=1
根据上面的公式可知,输出特征图大小为:
H / W i = H / W i i n + 2 p i − k i s i + 1 = 5 + 2 × 1 − 3 2 + 1 = 3 \begin{aligned} \mathrm{H / W}_i & = \frac{\mathrm{H / W}_i^{\mathrm{in}}+2p_i-k_i}{s_i}+1\\ & = \frac{5 + 2\times 1 - 3}{2} + 1\\ & = 3 \end{aligned} H/Wi=siH/Wiin+2pi−ki+1=25+2×1−3+1=3
即输出特征图的宽度和高度为
3
×
3
3 \times 3
3×3。我们发现,stride=1, padding=0 和 stride=2, padding=1 输出特征图的 宽度和高度 是一样的。
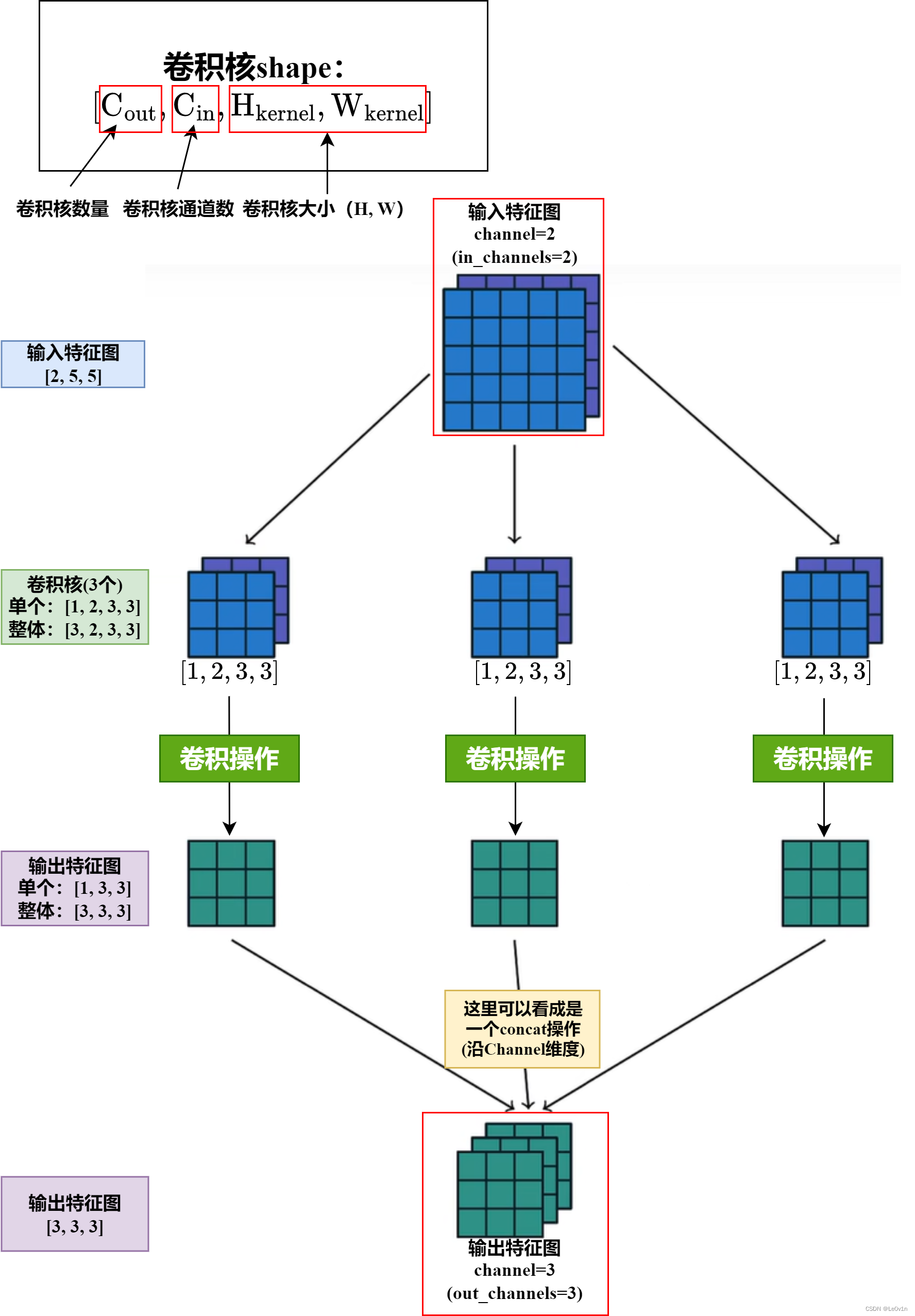
5.3 in_channels=2, out_channels=3, kernel_size=3, stride=1, padding=0
5.1 和 5.2 中都是单通道特征图在卷积中的运算,但在实际任务中,我们的输入图像一般是多通道的,特征图也是多通道的,因此我们看一下下面的这种情况。
5.4 ❗️卷积核注意事项❗️
5.4.1 输出特征图通道数(输出特征图数量)
输出特征图的通道数是由卷积核的个数决定的,因为一个卷积核生成一张特征图。即 out_channels 就是输出特征图的通道数。
5.4.2 卷积核个数(数量)
对于一个卷积层而言,卷积核的数量等于 out_channels,而不是 in_channels * out_channels。
在卷积层中,每个输出通道都有一个对应的卷积核。卷积核的形状是 (out_channels, in_channels, kernel_height, kernel_width),其中 out_channels 是输出通道的数量,而 in_channels 是输入通道的数量。这意味着每个输出通道都需要一个大小为 (in_channels, kernel_height, kernel_width) 的卷积核与输入通道进行卷积运算。
因此,卷积核的数量就是输出通道的数量 out_channels,而不是 in_channels * out_channels。每个输出通道对应一个卷积核,卷积核的数量等于输出通道的数量。
❗️注意❗️:卷积过程中卷积核的数量(即 out_channels)在 __init__ 方法中就已经确定好了,所以说这个卷积层的输出通道数就已经确定了。我们在模型训练过程中一般是不会突然改变某个 nn.Conv2d 层的 out_channels 参数 —— 其他参数也是同理(要记住 nn.Conv2d 是一个类而非一个函数)。
- 一旦实例化了
nn.Conv2d对象,并在__init__方法中指定了参数,这些参数就会在整个卷积层的生命周期中保持不变。- 模型的结构在训练过程中保持不变,参数的更新只发生在权重和偏置等可以学习的参数上,而不是在
nn.Conv2d层的配置参数上
5.5 设置 padding 使得 输入输出特征图尺寸不变
方法1:
padding = (kernel_size - 1) // 2 # kernel_size 必须为奇数
方法2:
padding = (kernel_size * 2 + 1) // 2 # kernel_size 可以为偶数
6. 滑动相乘实现 F.conv2d()
接下来我们将会按照这样的运算流程进行卷积的代码实现。
6.1 F.conv2d() 的代码实现(忽略 batch size 和 channel)
import torch
import torch.nn as nn
import torch.nn.functional as F
import math
def matrix_multiplication_for_conv2d(input, kernel, stride=1, padding=0, bias=None):
"""使用原始的矩阵运算实现二维卷积(先不考虑batch_size和channel维度)
Args:
input (Tensor): 输入特征图,形状为 [H, W]
kernel (Tensor): 卷积核,形状为 [kernel_h, kernel_w]
stride (int, optional): 步长. Defaults to 1.
padding (int, optional): 填充. Defaults to 0.
bias (Tensor, optional): 偏置. Defaults to None.
Returns:
_type_: 输出特征图
"""
# 是否需要进行padding
if padding > 0:
input = F.pad(input, (padding, padding, padding, padding)) # 上下左右都需要pad
# 获取输入大小
input_h, input_w = input.shape
kernel_h, kernel_w = kernel.shape
# 计算输出特征图尺寸(卷积尺寸向下取整)Note:先进行padding,所以在计算输出特征图尺寸时不用考虑padding的值了!
output_w = math.floor((input_w - kernel_w) / stride) + 1
output_h = math.floor((input_h - kernel_h) / stride) + 1
# 随机初始化一个要输出的矩阵
output = torch.zeros([output_h, output_w])
# 进行两层的遍历(先H再W)
for h in range(0, input_h - kernel_h + 1, stride): # 对高度进行遍历(步长为stride)
for w in range(0, input_w - kernel_w + 1, stride): # 对宽度进行遍历(步长为stride)
# 进行矩阵的逐元素相乘
region = input[h: h + kernel_h, w: w + kernel_w] # 取出要与卷积核进行点积的区域
output[int(h / stride), int(w / stride)] = torch.sum(region * kernel) # 进行点乘并赋值给输出的位置
# 偏置(应该先完成所有的卷积运算,然后再添加偏置值)
if bias is not None:
output = output + bias
return output
if __name__ == "__main__":
# 固定随机数种子
torch.manual_seed(10010)
# 输入特征图
input = torch.randn(size=[5, 5]) # BS, C, H, W
kernel = torch.randn([3, 3])# 卷积核参数
bias = torch.randn([1, ]) # 卷积核偏置 —— bias只与输出通道数有关(即卷积核个数)
# PyTorch的结果
res_pytorch = torch.nn.functional.conv2d(input=input.reshape(1, 1, input.shape[0], input.shape[1]),
weight=kernel.reshape(1, 1, kernel.shape[0], kernel.shape[1]),
stride=1,
padding=1,
bias=bias)
print(f"PyTorch的结果:\r\n{res_pytorch.squeeze()}")
#自己实现的结果
res = matrix_multiplication_for_conv2d(input=input,
kernel=kernel,
stride=1,
padding=1,
bias=bias)
print(f"自己实现的结果:\r\n{res}")
# 对比两个Tensor对应位置的浮点数是否接近
print(torch.allclose(res_pytorch, res)) # True
结果如下:
PyTorch的结果:
tensor([[-0.8682, 0.0836, 2.4579, 7.9269, -0.2708],
[-3.4977, -1.1559, 4.6909, -0.1927, 0.3715],
[-1.3349, -0.7388, -8.6954, -1.6454, 0.0757],
[-7.0991, -0.4209, 1.2751, 2.7073, -2.9031],
[ 0.1042, -0.1368, 2.0605, -1.1924, 0.0251]])
自己实现的结果:
tensor([[-0.8682, 0.0836, 2.4579, 7.9269, -0.2708],
[-3.4977, -1.1559, 4.6909, -0.1927, 0.3715],
[-1.3349, -0.7388, -8.6954, -1.6454, 0.0757],
[-7.0991, -0.4209, 1.2751, 2.7073, -2.9031],
[ 0.1042, -0.1368, 2.0605, -1.1924, 0.0251]])
6.2 F.conv2d() 的代码实现(实现 batch size 和 channel)
6.2.1 方法 1
import torch
import torch.nn as nn
import torch.nn.functional as F
import math
def matrix_multiplication_for_conv2d_completed(input, kernel, stride=1, padding=0, bias=None):
"""使用原始的矩阵运算实现二维卷积(支持多通道和batch维度)
Args:
input (Tensor): 输入特征图,形状为 [Batchsize, C, H, W]
kernel (Tensor): 卷积核,形状为 [out_channels, in_channels, kernel_h, kernel_w]
stride (int, optional): 步长. Defaults to 1.
padding (int, optional): 填充. Defaults to 0.
bias (Tensor, optional): 偏置. Defaults to None.
Returns:
Tensor: 输出特征图
"""
# 是否需要进行padding
if padding > 0:
input = F.pad(input, (padding, padding, padding, padding)) # 上下左右都需要pad
# 获取输入大小
batch_size, in_channels, input_h, input_w = input.shape
out_channels, _, kernel_h, kernel_w = kernel.shape # 第二个参数和 in_channels 是一样的
# 计算输出特征图尺寸(卷积尺寸向下取整)Note:先进行padding,所以在计算输出特征图尺寸时不用考虑padding的值了!
output_w = math.floor((input_w - kernel_w) / stride) + 1
output_h = math.floor((input_h - kernel_h) / stride) + 1
# 随机初始化一个要输出的矩阵
output = torch.zeros([batch_size, out_channels, output_h, output_w])
# 进行两层的遍历(先H再W)
for h in range(0, input_h - kernel_h + 1, stride): # 对高度进行遍历(步长为stride)
for w in range(0, input_w - kernel_w + 1, stride): # 对宽度进行遍历(步长为stride)
# 进行矩阵的逐元素相乘
region = input[:, :, h: h + kernel_h, w: w + kernel_w] # 取出要与卷积核进行点积的区域
output[:, :, int(h / stride), int(w / stride)] = torch.sum(region * kernel, dim=(1, 2, 3)) # 进行点乘并赋值给输出的位置
# 偏置(应该先完成所有的卷积运算,然后再添加偏置值)
if bias is not None:
output = output + bias.view(1, -1, 1, 1)
return output
if __name__ == "__main__":
# 固定随机数种子
torch.manual_seed(10010)
# 输入特征图
input = torch.randn(size=[2, 3, 5, 5]) # Batchsize, C, H, W
kernel = torch.randn([2, 3, 3, 3]) # 卷积核参数,形状为 [out_channels, in_channels, kernel_h, kernel_w]
bias = torch.randn([2, ]) # 卷积核偏置 —— bias只与输出通道数有关(即卷积核个数)
# PyTorch的结果
res_pytorch = F.conv2d(input=input, weight=kernel, stride=1, padding=1, bias=bias)
print(f"PyTorch的结果:\r\n{res_pytorch.squeeze()}")
#自己实现的结果
res = matrix_multiplication_for_conv2d_completed(input=input, kernel=kernel, stride=1, padding=1, bias=bias)
print(f"自己实现的结果:\r\n{res}")
# 对比两个Tensor对应位置的浮点数是否接近
print(torch.allclose(res_pytorch, res)) # True
结果如下:
PyTorch的结果:
tensor([[[[ 3.0275, 4.8720, -3.9974, 5.1608, 0.9514],
[ 12.4525, 7.4182, 4.6702, 9.7314, -4.3571],
[ -3.2892, 3.6016, 10.4584, 3.5384, 0.3544],
[ 8.7312, 2.6497, 9.4672, 1.7016, 2.4650],
[ 7.2345, 2.1328, 7.7006, 0.4131, 13.1020]],
[[ 5.9256, -5.6192, -4.8512, -3.4734, 1.9928],
[ 4.2990, -1.4098, 3.8647, -6.9448, -1.0597],
[ -6.0460, 8.2837, -4.8912, 0.2388, -4.4331],
[ 0.4701, 0.0266, -8.2944, -2.9790, -10.2942],
[ -3.5228, -0.0789, 2.3564, 0.3716, -0.5882]]],
[[[ -0.1347, 1.7058, 4.0682, 7.5516, 4.9627],
[ -2.8487, 4.7063, 7.4273, -4.6978, 4.9483],
[ 4.7545, 9.5539, -2.7510, 15.1170, 5.1214],
[ 6.2537, 0.9930, 10.9024, 14.6522, -6.8478],
[ -0.6205, 1.6231, 5.5700, 9.6074, 3.6440]],
[[ -0.5853, 7.7044, -1.2999, 1.1914, -4.6534],
[ -4.9776, -0.9076, 2.6359, -11.0334, 3.5623],
[ -3.4314, 2.2645, -4.6050, 0.9916, -3.6573],
[ 0.5469, -0.7690, 5.5431, -15.3839, -4.1287],
[ -5.7980, -0.1221, -6.2585, 0.1956, -0.7817]]]])
自己实现的结果:
tensor([[[[ 3.0275, 4.8720, -3.9974, 5.1608, 0.9514],
[ 12.4525, 7.4182, 4.6702, 9.7314, -4.3571],
[ -3.2892, 3.6016, 10.4584, 3.5384, 0.3544],
[ 8.7312, 2.6497, 9.4672, 1.7016, 2.4650],
[ 7.2345, 2.1328, 7.7006, 0.4131, 13.1020]],
[[ -0.5853, 7.7044, -1.2999, 1.1914, -4.6534],
[ -4.9776, -0.9076, 2.6359, -11.0334, 3.5623],
[ -3.4314, 2.2645, -4.6050, 0.9916, -3.6573],
[ 0.5469, -0.7690, 5.5431, -15.3839, -4.1287],
[ -5.7980, -0.1221, -6.2585, 0.1956, -0.7817]]],
[[[ 3.0275, 4.8720, -3.9974, 5.1608, 0.9514],
[ 12.4525, 7.4182, 4.6702, 9.7314, -4.3571],
[ -3.2892, 3.6016, 10.4584, 3.5384, 0.3544],
[ 8.7312, 2.6497, 9.4672, 1.7016, 2.4650],
[ 7.2345, 2.1328, 7.7006, 0.4131, 13.1020]],
[[ -0.5853, 7.7044, -1.2999, 1.1914, -4.6534],
[ -4.9776, -0.9076, 2.6359, -11.0334, 3.5623],
[ -3.4314, 2.2645, -4.6050, 0.9916, -3.6573],
[ 0.5469, -0.7690, 5.5431, -15.3839, -4.1287],
[ -5.7980, -0.1221, -6.2585, 0.1956, -0.7817]]]])
6.2.2 方法 2
import torch
import torch.nn as nn
import torch.nn.functional as F
import math
def matrix_multiplication_for_conv2d_full(input, kernel, stride=1, padding=0, bias=None):
"""使用原始的矩阵运算实现二维卷积(支持多通道和batch维度)
Args:
input (Tensor): 输入特征图,形状为 [Batchsize, C, H, W]
kernel (Tensor): 卷积核,形状为 [out_channels, in_channels, kernel_h, kernel_w]
stride (int, optional): 步长. Defaults to 1.
padding (int, optional): 填充. Defaults to 0.
bias (Tensor, optional): 偏置. Defaults to None.
Returns:
Tensor: 输出特征图
"""
# 是否需要进行padding
if padding > 0:
# 上下左右都需要pad
input = F.pad(input, (padding, padding, padding, padding, 0, 0, 0, 0))
# 获取输入大小
batch_size, in_channels, input_h, input_w = input.shape
out_channels, in_channels, kernel_h, kernel_w = kernel.shape
# 计算输出特征图尺寸(卷积尺寸向下取整)Note:先进行padding,所以在计算输出特征图尺寸时不用考虑padding的值了!
output_w = math.floor((input_w - kernel_w) / stride) + 1
output_h = math.floor((input_h - kernel_h) / stride) + 1
# 随机初始化一个要输出的矩阵
output = torch.zeros([batch_size, out_channels, output_h, output_w]) # BS, C, H, W
for bs in range(batch_size): # 样本层
for out_c in range(out_channels): # 输出通道层
for in_c in range(in_channels): # 输入通道层
for h in range(0, input_h - kernel_h + 1, stride): # 高度层
for w in range(0, input_w - kernel_w + 1, stride): # 宽度层
# 进行矩阵的逐元素相乘
region = input[bs, in_c, h: h + kernel_h, w: w + kernel_w] # 取出要与卷积核进行点积的区域
output[bs, out_c, int(h / stride), int(w / stride)] += torch.sum(region * kernel[out_c, in_c])
# 偏置(应该先完成所有的卷积运算,然后再添加偏置值)
if bias is not None:
output[bs, out_c] += bias[out_c]
return output
if __name__ == "__main__":
# 固定随机数种子
torch.manual_seed(10010)
# 输入特征图
input = torch.randn(size=[2, 2, 5, 5]) # BS, C, H, W
kernel = torch.randn([3, input.shape[1], 3, 3]) # out_channels, in_channels, kernel_h, kernel_w
bias = torch.randn([kernel.shape[0]]) # 卷积核偏置 —— bias只与输出通道数有关(即卷积核个数)
# PyTorch的结果
res_pytorch = torch.nn.functional.conv2d(input=input,
weight=kernel,
stride=2,
padding=1,
bias=bias)
print(f"PyTorch的结果:\r\n{res_pytorch.squeeze()}")
# 自己实现的结果
res = matrix_multiplication_for_conv2d_full(input=input,
kernel=kernel,
stride=2,
padding=1,
bias=bias)
print(f"自己实现的结果:\r\n{res}")
# 对比两个Tensor对应位置的浮点数是否接近
print(torch.allclose(res_pytorch, res)) # True
结果:
PyTorch的结果:
tensor([[[[-3.6928e+00, -2.6268e+00, 8.4024e+00],
[-8.5057e-01, 1.0824e+01, 2.3715e+00],
[ 5.3372e+00, 1.6813e+00, 4.2187e-01]],
[[-3.0795e+00, 4.0927e+00, 3.4418e+00],
[ 8.3022e+00, 5.9172e+00, 5.8364e-03],
[-2.1851e+00, -3.3452e+00, 8.7408e-01]],
[[-9.8562e-01, -2.9137e+00, -2.7892e+00],
[-1.6306e+00, -2.7707e+00, -1.7414e+00],
[-1.5909e+00, 1.9428e+00, -5.3450e+00]]],
[[[-4.7734e+00, 1.0357e+01, -7.5430e-01],
[ 4.4884e+00, 4.8198e-01, -2.0881e+00],
[-1.9886e+00, -3.4768e+00, -1.6048e-01]],
[[ 3.5886e+00, 2.7784e+00, -5.1504e+00],
[ 2.8218e+00, 7.7608e-01, 3.2618e+00],
[ 1.9104e+00, 5.3918e+00, -1.0451e+00]],
[[-9.3626e-01, 6.1895e-01, -4.1977e+00],
[ 1.8835e+00, -8.8371e+00, -1.2878e+00],
[ 2.4139e+00, -1.1291e+00, 1.2844e+00]]]])
自己实现的结果:
tensor([[[[-3.6928e+00, -2.6268e+00, 8.4024e+00],
[-8.5057e-01, 1.0824e+01, 2.3715e+00],
[ 5.3372e+00, 1.6813e+00, 4.2187e-01]],
[[-3.0795e+00, 4.0927e+00, 3.4418e+00],
[ 8.3022e+00, 5.9172e+00, 5.8365e-03],
[-2.1851e+00, -3.3452e+00, 8.7408e-01]],
[[-9.8562e-01, -2.9137e+00, -2.7892e+00],
[-1.6306e+00, -2.7707e+00, -1.7414e+00],
[-1.5909e+00, 1.9428e+00, -5.3450e+00]]],
[[[-4.7734e+00, 1.0357e+01, -7.5430e-01],
[ 4.4884e+00, 4.8198e-01, -2.0881e+00],
[-1.9886e+00, -3.4768e+00, -1.6048e-01]],
[[ 3.5886e+00, 2.7784e+00, -5.1504e+00],
[ 2.8218e+00, 7.7608e-01, 3.2618e+00],
[ 1.9104e+00, 5.3918e+00, -1.0451e+00]],
[[-9.3626e-01, 6.1895e-01, -4.1977e+00],
[ 1.8835e+00, -8.8371e+00, -1.2878e+00],
[ 2.4139e+00, -1.1291e+00, 1.2844e+00]]]])
7. [im2col] 向量内积实现 F.conv2d()
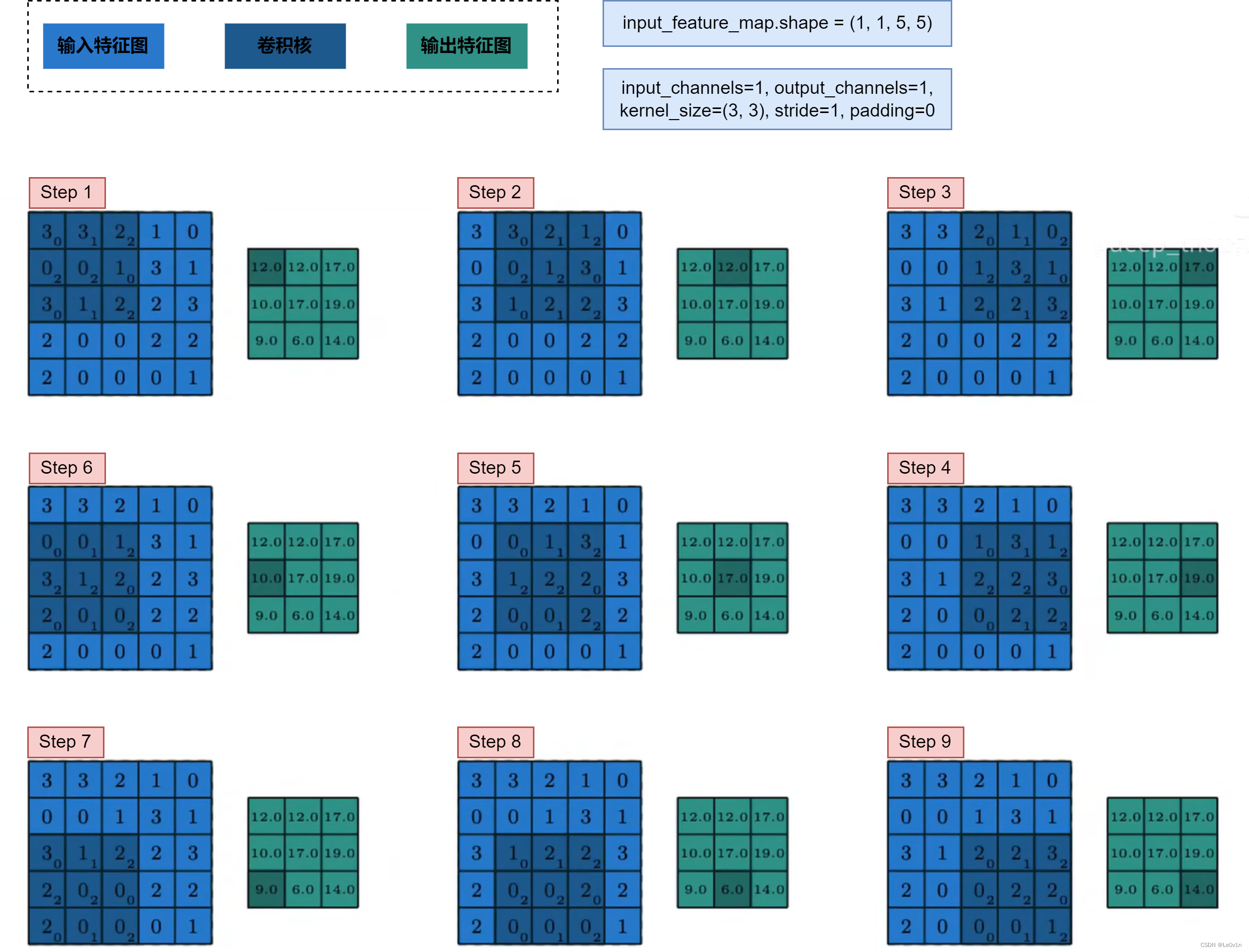
我们再看一下卷积的运算过程。之前在第六章中用滑动的方式(就是图中这样的方式)来实现 F.conv2d()。我们再回顾一下这个过程。这个次卷积一共有 9 步,但是经验告诉我们,for 循环这样的方式并不是高效的。GPU 之所以运算高效是因为它可以实现并行计算,那么我们应该如何让卷积运算并行计算呢?
在第六章的代码实现中,我们会有一个名为 region 的变量,里面存放的是即将与卷积核进行计算的特征图区域,那么这个区域我们其实是可以展平的(卷积核也是可以展平的),使其变为行向量(卷积核为列向量)。之后我们再将这个两个向量进行矩阵乘法。行向量与列向量相乘可以得到一个标量。但是这样和第六章中没有什么太大的区别,因为还是需要 9 步才可以计算完毕,那么我们应该如何让步骤减少呢?
我们是不是可以直接将所有的 region 都取出来,并将其展平为行向量,再将这些行向量堆叠起来,是不是就会得到一个
9
×
9
9 \times 9
9×9 的方阵?之后我们让这个矩阵与展平后的卷积核进行矩阵乘法,最后再对其进行 reshape,这样就一步得到我们的输出矩阵了,从而实现步骤的大幅度缩减。
那么我们还有没有其他方式来增加计算效率呢?
答案是肯定的。我们能不能不用 region 变量呢?这里有个问题,那就是点积需要双方的尺寸一致,如果不取出要卷积的部分,那么需要对卷积核的尺寸进行修改。这里使用 padding 即可。将不需要卷积的地方用 0 填充,这样就可以直接进行点积了。上图中,我们的输入特征图尺寸为 25×25,那我们可以将卷积核也填充到 25×25 的尺寸。
这里我们不用这种实现方式,该实现方式是为了以后会用到的转置卷积作为引子
我们再梳理一下第一种方式。在卷积运算中,我们可以利用矩阵乘法的性质来进行高效的并行计算,从而减少卷积运算的步骤。具体步骤如下:
- 将每个与卷积核进行计算的特征图区域 F i \mathcal{F}_i Fi 展平为行向量。
- 将这些行向量堆叠起来,形成一个矩阵 F \mathcal{F} F(可以看作是由多个行向量组成的矩阵,每行代表一个特征图区域)。
- 将卷积核也展平为列向量 V \mathcal{V} V。
- 对步骤 2 中得到的矩阵 F \mathcal{F} F 与步骤 3 中得到的列向量 V \mathcal{V} V 进行矩阵乘法,得到一个包含多个标量的列向量 V ′ \mathcal{V'} V′。
- 将得到的列向量
V
′
\mathcal{V'}
V′ 进行
reshape操作,得到最终的输出特征图。
通过这种方式,我们可以一步得到输出特征图,从而大幅度缩减了卷积运算的步骤,提高了运算效率。这种方式通常被称为 "im2col",即将输入特征图转换为列(column)的形式。在深度学习框架中,很多卷积操作都采用了类似的优化策略,从而加快了计算速度。
卷积核权值共享:假设有一个 3×3 的卷积核,它在输入特征图上进行卷积操作。无论这个卷积核是在输入特征图的左上角、右下角或者其他任意位置,它使用的权重参数都是相同的。
7.1 F.conv2d() 的代码实现(忽略 batch size 和 channel)
import torch
import torch.nn as nn
import torch.nn.functional as F
import math
def matrix_multiplication_for_conv2d_flatten_version(input, kernel, stride=1, padding=0, bias=None):
"""使用 im2col 的方式实现二维卷积(先不考虑batch_size和channel维度)
Args:
input (Tensor): 输入特征图,形状为 [H, W]
kernel (Tensor): 卷积核,形状为 [kernel_h, kernel_w]
stride (int, optional): 步长. Defaults to 1.
padding (int, optional): 填充. Defaults to 0.
bias (Tensor, optional): 偏置. Defaults to None.
Returns:
_type_: 输出特征图
"""
# 是否需要进行padding
if padding > 0:
# 上下左右都需要pad
input = F.pad(input, (padding, padding, padding, padding))
# 获取输入大小
input_h, input_w = input.shape
kernel_h, kernel_w = kernel.shape
# 计算输出特征图尺寸(卷积尺寸向下取整)Note:先进行padding,所以在计算输出特征图尺寸时不用考虑padding的值了!
output_w = math.floor((input_w - kernel_w) / stride) + 1
output_h = math.floor((input_h - kernel_h) / stride) + 1
# 随机初始化一个要输出的矩阵
output = torch.zeros([output_h, output_w])
# 初始化 region_matrix: 存储所有的展平后的region
# .numel: 返回Tensor中元素的个数
region_matrix = torch.zeros([output.numel(), kernel.numel()])
# [step 3] 将卷积核也展平为列向量
kernel_vector = kernel.reshape(kernel.numel(), 1) # 直接将其变为列向量即可
# 计数器,用于跟踪当前行的索引
row_index = 0
# 进行两层的遍历(先H再W)
for h in range(0, input_h - kernel_h + 1, stride): # 对高度进行遍历(步长为stride)
for w in range(0, input_w - kernel_w + 1, stride): # 对宽度进行遍历(步长为stride)
# 进行矩阵的逐元素相乘
region = input[h: h + kernel_h, w: w + kernel_w] # 取出要与卷积核进行点积的区域
# [step 1] 将每个与卷积核进行计算的特征图区域展平为行向量
# torch.flatten(): 是 PyTorch 中用于将输入张量展平为一维张量的函数。它的作用是将输入的多维张量压缩成一维,并且保持原来的顺序不变。
region_vector = torch.flatten(region)
# [step 2] 将这些行向量堆叠起来,形成一个矩阵(可以看作是由多个行向量组成的矩阵,每行代表一个特征图区域)
region_matrix[row_index] = region_vector
row_index += 1 # 更新计数器
# [step 4] 对步骤 2 中得到的矩阵与步骤 3 中得到的列向量进行矩阵乘法,得到一个包含多个标量的列向量
output_matrix = region_matrix @ kernel_vector
# [step 5] 将得到的列向量进行 reshape 操作,得到最终的输出特征图
output = output_matrix.reshape(output_h, output_w)
# 偏置(应该先完成所有的卷积运算,然后再添加偏置值)
if bias is not None:
output = output + bias
return output
if __name__ == "__main__":
# 固定随机数种子
torch.manual_seed(10010)
# 输入特征图
input = torch.randn(size=[5, 5]) # BS, C, H, W
kernel = torch.randn([3, 3]) # 卷积核参数
bias = torch.randn([1, ]) # 卷积核偏置 —— bias只与输出通道数有关(即卷积核个数)
# PyTorch的结果
res_pytorch = torch.nn.functional.conv2d(input=input.reshape(1, 1, input.shape[0], input.shape[1]),
weight=kernel.reshape(1, 1, kernel.shape[0], kernel.shape[1]),
stride=2,
padding=1,
bias=bias)
print(f"PyTorch的结果:\r\n{res_pytorch.squeeze()}")
# 自己实现的结果
res = matrix_multiplication_for_conv2d_flatten_version(input=input,
kernel=kernel,
stride=2,
padding=1,
bias=bias)
print(f"自己实现的结果:\r\n{res}")
# 对比两个Tensor对应位置的浮点数是否接近
print(torch.allclose(res_pytorch, res)) # True
结果:
PyTorch的结果:
tensor([[-0.8682, 2.4579, -0.2708],
[-1.3349, -8.6954, 0.0757],
[ 0.1042, 2.0605, 0.0251]])
自己实现的结果:
tensor([[-0.8682, 2.4579, -0.2708],
[-1.3349, -8.6954, 0.0757],
[ 0.1042, 2.0605, 0.0251]])
7.2 F.conv2d() 的代码实现(实现 batch size 和 channel)
import torch
import torch.nn.functional as F
import math
def matrix_multiplication_for_conv2d_flatten_version_completed(input, weight, stride=1, padding=0, bias=None):
"""使用 im2col 的方式实现二维卷积
Args:
input (Tensor): 输入特征图,形状为 [batch_size, in_channels, H, W]
weight (Tensor): 卷积核,形状为 [out_channels, in_channels, kernel_h, kernel_w]
stride (int, optional): 步长. Defaults to 1.
padding (int, optional): 填充. Defaults to 0.
bias (Tensor, optional): 偏置. Defaults to None.
Returns:
_type_: 输出特征图
"""
# 是否需要进行padding
if padding > 0:
# 上下左右都需要pad
input = F.pad(input, (padding, padding, padding, padding))
batch_size, in_channels, input_h, input_w = input.shape
out_channels, _, kernel_h, kernel_w = weight.shape
# 计算输出特征图尺寸(卷积尺寸向下取整)Note:先进行padding,所以在计算输出特征图尺寸时不用考虑padding的值了!
output_w = math.floor((input_w - kernel_w) / stride) + 1
output_h = math.floor((input_h - kernel_h) / stride) + 1
# 随机初始化一个要输出的矩阵
output = torch.zeros([batch_size, out_channels, output_h, output_w])
for b in range(batch_size):
for o in range(out_channels):
for i in range(in_channels):
# 初始化 region_matrix: 存储所有的展平后的region
region_matrix = torch.zeros([output_h * output_w, kernel_h * kernel_w])
kernel_vector = weight[o, i].reshape(-1, 1)
row_index = 0
for h in range(0, input_h - kernel_h + 1, stride): # 对高度进行遍历(步长为stride)
for w in range(0, input_w - kernel_w + 1, stride): # 对宽度进行遍历(步长为stride)
region_vector = torch.flatten(input[b, i, h: h + kernel_h, w: w + kernel_w])
region_matrix[row_index] = region_vector
row_index += 1 # 更新计数器
output_matrix = region_matrix @ kernel_vector
output[b, o] += output_matrix.reshape(output_h, output_w)
# 偏置(应该先完成所有的卷积运算,然后再添加偏置值)
if bias is not None:
output = output + bias.view(1, -1, 1, 1)
return output
if __name__ == "__main__":
# 固定随机数种子
torch.manual_seed(10010)
# 输入特征图
input = torch.randn(size=[1, 3, 5, 5]) # BS, C, H, W
weight = torch.randn([5, 3, 5, 5]) # 卷积核参数
bias = torch.randn([weight.shape[0], ]) # 卷积核偏置 —— bias只与输出通道数有关(即卷积核个数)
# PyTorch的结果
res_pytorch = torch.nn.functional.conv2d(input=input,
weight=weight,
stride=2,
padding=1,
bias=bias)
print(f"PyTorch的结果:\r\n{res_pytorch}")
# 自己实现的结果
res = matrix_multiplication_for_conv2d_flatten_version_completed(input=input,
weight=weight,
stride=2,
padding=1,
bias=bias)
print(f"自己实现的结果:\r\n{res}")
# 对比两个Tensor对应位置的浮点数是否接近
print(torch.allclose(res_pytorch, res)) # True
结果:
PyTorch的结果:
tensor([[[[ 3.5696, -2.3912],
[ 6.7484, 3.2763]],
[[ 8.9917, -1.4192],
[ -8.8775, -2.5190]],
[[ -3.4709, -12.0758],
[ 5.2905, -1.0210]],
[[ 14.8612, 11.0591],
[ 9.6713, -2.3926]],
[[ -3.4078, -11.3381],
[ -8.7323, 0.7613]]]])
自己实现的结果:
tensor([[[[ 3.5696, -2.3912],
[ 6.7484, 3.2763]],
[[ 8.9917, -1.4192],
[ -8.8775, -2.5190]],
[[ -3.4709, -12.0758],
[ 5.2905, -1.0210]],
[[ 14.8612, 11.0591],
[ 9.6713, -2.3926]],
[[ -3.4078, -11.3381],
[ -8.7323, 0.7613]]]])