文章目录
节课开始,我们将以分类深层神经网络为例,为大家展示神经网络的学习和训练过程。在介绍PyTorch的基本工具AutoGrad库时,我们系统地介绍过数学中的优化问题和优化思想,我们介绍了最小二乘法以及梯度下降法这两个入门级优化算法的具体操作,并使用AutoGrad库实现了他们。接下来,我们将从梯度下降法向外拓展,介绍神经网络的损失函数、常用优化算法等信息,实现神经网络的学习和迭代。本节主要讲解神经网络常用的损失函数,并在PyTorch中实现这些函数。
一、机器学习中的优化思想
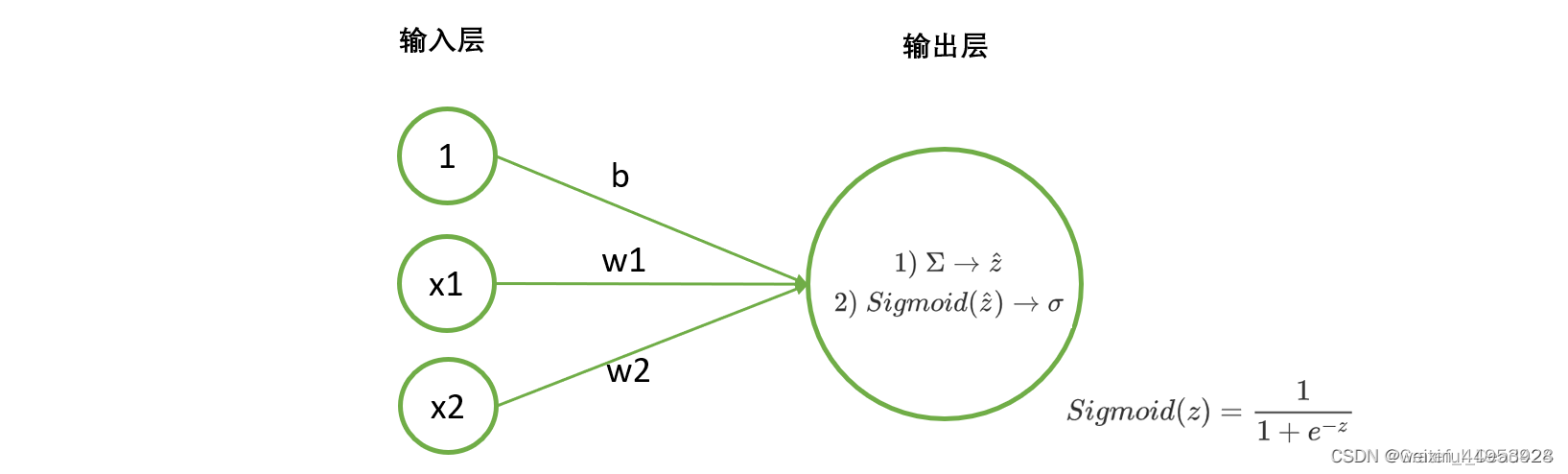
在之前的学习中,我们建立神经网络时总是先设定好与的值(或者由我们调用的PyTorch类帮助我们随机生成权重向量),接着通过加和求出z ,再在z 上嵌套sigmoid或者softmax函数,最终获得神经网络的输出。我们的代码及计算流程,总是从神经网络的左侧向右侧计算的。之前我们提到过,这是神经网络的正向传播过程。但很明显,这并不是神经网络算法的全流程,这个流程虽然可以输出预测结果,但却无法保证神经网络的输出结果与真实值接近。
在讲解线性回归时,我们提起过,线性回归的任务就是构造一个预测函数来映射输入的特征矩阵X 和标签值y 的线性关系。构造预测函数核心就是找出模型的权重向量w ,并令线性回归的输出结果与真实值相近,也就是求解线性方程组中的w 和b 。对神经网络而言也是如此,我们的核心任务是求解一组最适合的w 和b ,令神经网络的输出结果与真实值接近。找寻这个w 和b 的过程就是“学习”,也叫做“训练”或者“建模”。
那我们如何评价和是否合适呢?我们又如何衡量我们的输出结果与真实值之间的差异大小呢?此时,我们就需要使用机器学习中通用的优化流程了。在讲解autograd的时候,其实我们已经提过这个优化流程,在这里我们稍微复习一下:
1)提出基本模型,明确目标
我们的基本模型就是我们自建的神经网络架构,我们需要求解的就是神经网络架构中的权重向量w ww。
2)确定损失函数/目标函数
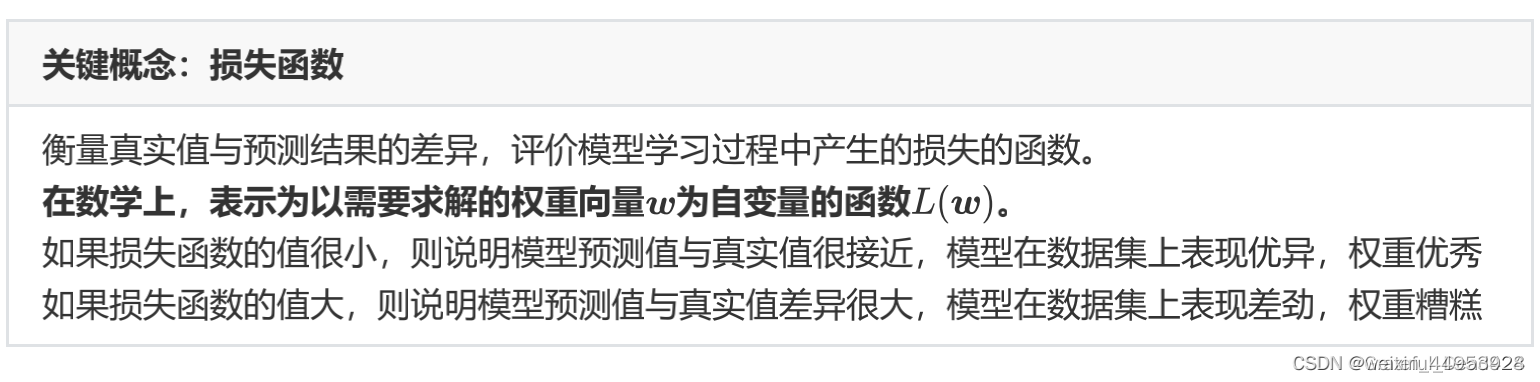
我们需要定义某个评估指标,用以衡量模型权重为w 的情况下,预测结果与真实结果的差异。当真实值与预测值差异越大时,我们就认为神经网络学习过程中丢失了许多信息,丢失的这部分被形象地称为”损失“,因此评估真实值与预测值差异的函数被我们称为“损失函数”。
我们希望损失函数越小越好,以此,我们将问题转变为求解函数L ( w )的最小值所对应的自变量w 。但是,损失函数往往不是一个简单的函数,求解复杂函数就需要复杂的数学工具。在这里,我们使用的数学工具可能有两部分:
- 将损失函数L ( w ) 转变成凸函数的数学方法,常见的有拉格朗日变换等
- 在凸函数上求解L ( w ) 的最小值对应的w 的方法,也就是以梯度下降为代表的优化算法
3)确定适合的优化算法
4)利用优化算法,最小化损失函数,求解最佳权重(训练)
之前我们在线性回归上走过这个全流程。对线性回归,我们的损失函数是SSE,优化算法是最小二乘法和梯度下降法,两者都是对机器学习来说非常重要的优化算法。但遗憾的是,最小二乘法作为入门级优化算法,有较多的假设和先决条件,不足以应对神经网络需要被应用的各种复杂环境。梯度下降法应用广泛,不过也有很多问题需要改进。接下来,我将主要以分类深层神经网络为例来介绍神经网络中所使用的入门级损失函数及优化算法。
二、回归:误差平方和SSE
对于回归类神经网络而言,最常见的损失函数是SSE(Sum of the Squared Errors),现在已经是我们第三次见到SSE的公式了:
在PyTorch中,我们可以简单通过以下代码调用MSE:
import torch
from torch.nn import MSELoss #类
yhat = torch.randn(size=(50,),dtype=torch.float32)
y = torch.randn(size=(50,),dtype=torch.float32)
criterion = MSELoss() #实例化
loss = criterion(yhat,y)
loss #没有设置随机数种子,所以每次运行的数字都会不一致
#tensor(1.5714)
#在MSELoss中有重要的参数,reduction
#当reduction = "mean" (默认也是mean),则输出MSE
#当reduction = "sum",则输出SSE
criterion = MSELoss(reduction = "mean") #实例化
criterion(yhat,y)
#tensor(1.5714)
criterion = MSELoss(reduction = "sum")
criterion(yhat,y)
#tensor(78.5707)
三、二分类交叉熵损失函数
在这一节中,我们将介绍二分类神经网络的损失函数:二分类交叉熵损失函数(Binary Cross Entropy Loss),也叫做对数损失(log loss)。这个损失函数被广泛地使用在任何输出结果是二分类的神经网络中,即不止限于单层神经网络,还可被拓展到多分类中,因此理解二分类交叉熵损失是非常重要的一环。大多数时候,除非特殊声明为二分类,否则提到交叉熵损失,我们会默认算法的分类目标是多分类。
二分类交叉熵损失函数是由极大似然估计推导出来的,对于有m个样本的数据集而言,在全部样本上的平均损失写作:
1、 极大似然估计求解二分类交叉熵损失
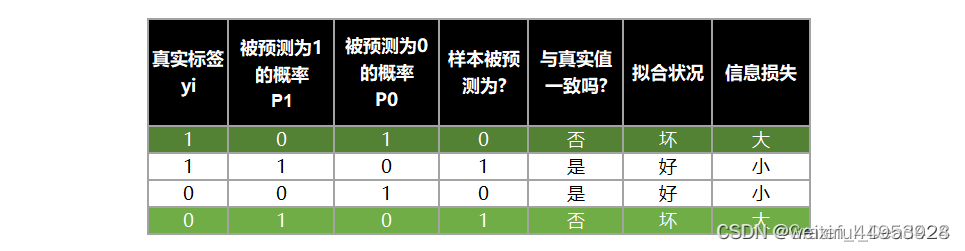
二分类交叉熵损失函数是怎么来的呢?为什么这个函数就能够代表二分类的时候,真实值与预测值的差异呢?
在这里,我们基于极大似然法来推导交叉熵损失,这个推导过程能够帮助我们充分了解交叉熵损失的含义,以及为什么的最小化能够实现模型在数据集上的拟合最好。
在二分类的例子中,我们的“任意事件”就是每个样本的分类都正确,对数似然函数的负数就是我们的损失函数。接下来,我们来看看逻辑回归的对数似然函数是怎样构筑的。
- 构筑对数似然函数
二分类神经网络的标签是[0,1],此标签服从伯努利分布(即0-1分布),因此可得:
2.用tensor实现二分类交叉熵损失
详细请看:https://blog.csdn.net/Grateful_Dead424/article/details/122332511?spm=1001.2014.3001.5502
现在,让我们在PyTorch中来实现二分类交叉熵损失函数。首先使用基本的tensor方法来试试看,以加深我们对二分类交叉熵损失的印象:
import torch
import time
N = 3*pow(10,3)
torch.random.manual_seed(420)
X = torch.rand((N,4),dtype=torch.float32)
w = torch.rand((4,1),dtype=torch.float32,requires_grad=True)
y = torch.randint(low=0,high=2,size=(N,1),dtype=torch.float32) #high取不到
zhat = torch.mm(X,w)
sigma = torch.sigmoid(zhat)
Loss = -(1/N)*torch.sum((1-y)*torch.log(1-sigma)+y*torch.log(sigma)) #底数默认为e
Loss
#tensor(0.7962, grad_fn=<MulBackward0>)
3 用PyTorch中的类实现二分类交叉熵损失
在PyTorch当中,我们有多种方式可以调用二分类交叉熵损失函数
对于二分类交叉熵损失,nn提供了两个类:BCEWithLogitsLoss以及BCELoss。虽然PyTorch官方没有直接明确,但实际上两个函数所需要输入的参数不同。
BCEWithLogitsLoss内置了sigmoid函数与交叉熵函数,它会自动计算输入值的sigmoid值,因此需要输入zhat与真实标签,且顺序不能变化,zhat必须在前。
相对的,BCELoss中只有交叉熵函数,没有sigmoid层,因此需要输入sigma与真实标签,且顺序不能变化。
同时,这两个函数都要求预测值与真实标签的数据类型以及结构(shape)必须相同,否则运行就会报错。
接下来,我们来看看这两个类是如何使用的:
import torch.nn as nn
#调用nn模块下的类
criterion = nn.BCELoss() #实例化
loss = criterion(sigma,y) #真实标签在后
loss
#tensor(0.8685, grad_fn=<BinaryCrossEntropyBackward0>)
criterion2 = nn.BCEWithLogitsLoss() #实例化
loss = criterion2(zhat,y) #真实标签在后
loss
#tensor(0.8685, grad_fn=<BinaryCrossEntropyWithLogitsBackward0>)
可以看出,两个类的结果是一致的。根据PyTorch官方的公告,他们更推荐使用BCEWithLogitsLoss这个内置了sigmoid函数的类。内置的sigmoid函数可以让精度问题被缩小(因为将指数运算包含在了内部),以维持算法运行时的稳定性,即是说当数据量变大、数据本身也变大时,BCELoss类产生的结果可能有精度问题。所以,当我们的输出层使用sigmoid函数时,我们就可以使用BCEWithLogitsLoss作为损失函数。
与MSELoss相同,二分类交叉熵的类们也有参数reduction,默认是”mean“,表示求解所有样本平均的损失,也可换为”sum”,要求输出整体的损失。以及,还可以使用选项“none”,表示不对损失结果做任何聚合运算,直接输出每个样本对应的损失矩阵。
criterion2 = nn.BCEWithLogitsLoss(reduction = "mean")
loss = criterion2(zhat,y)
loss
#tensor(0.8685, grad_fn=<BinaryCrossEntropyWithLogitsBackward0>)
criterion2 = nn.BCEWithLogitsLoss(reduction = "sum")
loss = criterion2(zhat,y)
loss
#tensor(2605616.5000, grad_fn=<BinaryCrossEntropyWithLogitsBackward0>)
criterion2 = nn.BCEWithLogitsLoss(reduction = "none")
loss = criterion2(zhat,y)
loss
#tensor([[1.3102],
# [0.3155],
# [0.4247],
# ...,
# [0.1727],
# [0.1716],
# [0.1673]], grad_fn=<BinaryCrossEntropyWithLogitsBackward0>)
第二种方法很少用,我们了解一下即可:
和nn中的类们相似,名称中带有Logits的是内置了sigmoid功能的函数,没有带Logits的,是只包含交叉熵损失的函数。对于含有sigmoid功能的函数,我们需要的输入是zhat与标签,不含sigmoid的函数我们则需要输入sigma与标签。同样的,这两个函数对输入有严格的要求,输入的预测值必须与标签结构一致、数据类型一致。我们来看看他们的运行结果:
from torch.nn import functional as F #直接调用functional库中的计算函数
F.binary_cross_entropy_with_logits(zhat,y)
#tensor(0.8685, grad_fn=<BinaryCrossEntropyWithLogitsBackward0>)
F.binary_cross_entropy(sigma,y)
#tensor(0.8685, grad_fn=<BinaryCrossEntropyBackward0>)
在这里,两个函数的运行结果是一致的。同样的,PyTorch官方推荐的是内置sigmoid功能的函数binary_cross_entropy_with_logits。通常来说,我们都使用类,不使用函数。虽然代码会因此变得稍稍有点复杂,但为了代码的稳定性与日后维护,使用类是更好的选择。当然,在进行代码演示和快速测算的时候,使用函数或者类都没有问题。
四、多分类交叉熵损失函数
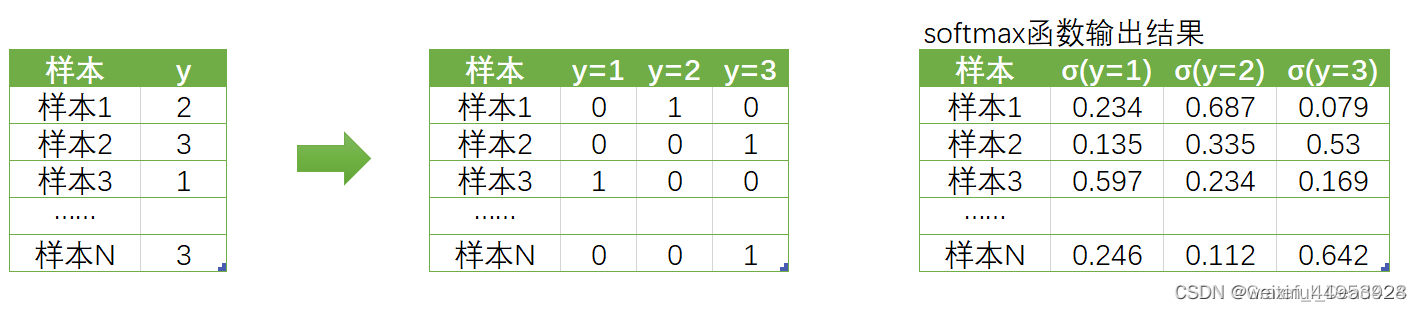
1. 由二分类推广到多分类
因此,我们对多分类的标签做出了如下变化:
2 用PyTorch实现多分类交叉熵损失
在PyTorch中实现交叉熵函数的时候,有两种办法:
- 调用logsoftmax和NLLLoss实现
import torch
import torch.nn as nn
N = 3*pow(10,2)
torch.random.manual_seed(420)
X = torch.rand((N,4),dtype=torch.float32)
w = torch.rand((4,3),dtype=torch.float32,requires_grad=True)
#定义y时应该怎么做?应该设置为矩阵吗?
y = torch.randint(low=0,high=3,size=(N,),dtype=torch.float32)
zhat = torch.mm(X,w) #从这里开始调用softmax和NLLLoss
logsm = nn.LogSoftmax(dim=1) #实例化
logsigma = logsm(zhat)
criterion = nn.NLLLoss() #实例化
#由于交叉熵损失需要将标签转化为独热形式,因此不接受浮点数作为标签的输入
#对NLLLoss而言,需要输入logsigma
criterion(logsigma,y.long()) #y一维、整型
#tensor(1.1591, grad_fn=<NllLossBackward0>)
- 直接调用CrossEntropyLoss
criterion = nn.CrossEntropyLoss()
#对打包好的CorssEnrtopyLoss而言,只需要输入zhat
criterion(zhat,y.long()) #一维、整型
#tensor(1.1591, grad_fn=<NllLossBackward0>)
可以发现,两种输出方法得到的损失函数结果是一致的。与其他损失函数一致,CrossEntropyLoss也有参数reduction,可以设置为mean、sum以及None,大家可以自行尝试其代码并查看返回结果。
无论时二分类还是多分类,PyTorch都提供了包含输出层激活函数和不包含输出层激活函数的类两种选择。在实际神经网络建模中,类可以被放入定义好的Model类中去构建神经网络的结构,因此是否包含激活函数,就需要由用户来自行选择。
- 重视展示网络结构和灵活性,应该使用不包含输出层激活函数的类
通常在Model类中,__init__中层的数量与forward函数中对应的激活函数的数量是一致的,如果我们使用内置sigmoid/logsoftmax功能的类来计算损失函数,forward函数在定义时就会少一层(输出层),网络结构展示就不够简单明了,对于结构复杂的网络而言,结构清晰就更为重要。同时,如果激活函数是单独写的,要修改激活函数就变得很容易,如果混在损失函数中,要修改激活函数时就得改掉整个损失函数的代码,不利于维护。
- 重视稳定性和运算精度,使用包含输出层激活函数的类
如果在一个Model中,很长时间我们都不会修改输出层的激活函数,并且模型的稳定运行更为要紧,我们就使用内置了激活函数的类来计算损失函数。同时,就像之前提到的,内置激活函数可以帮助我们推升运算的精度。
因此,选择哪种损失函数的实现方式,最终还要看我们的需求。
有了损失函数,我们终于要开始进行求解了。下一部分我们来讲解神经网络的入门级优化算法:小批量随机梯度下降