Bootstrap

从头搭建一个深度学习框架

从头搭建一个深度学习框架

转自：Build a Deep Learning Framework From Scratch

代码：https://github.com/borgwang/tinynn

在这里插入图片描述

当前深度学习框架越来越成熟，对于使用者而言封装程度越来越高，好处就是现在可以非常快速地将这些框架作为工具使用，用非常少的代码就可以进行实验，坏处就是可能背后地实现都被隐藏起来了。在这篇文章里笔者将带大家一起从头设计和实现一个轻量级的（大约 200 行）、易于扩展的深度学习框架 tinynn，希望对大家了解深度学习框架的基本设计和实现有一定的帮助。

本文首先会从深度学习的流程开始分析，对神经网络中的关键组件抽象，确定基本框架；然后再对框架里各个组件进行代码实现；最后基于这个框架实现了一个 MNIST 分类的示例。

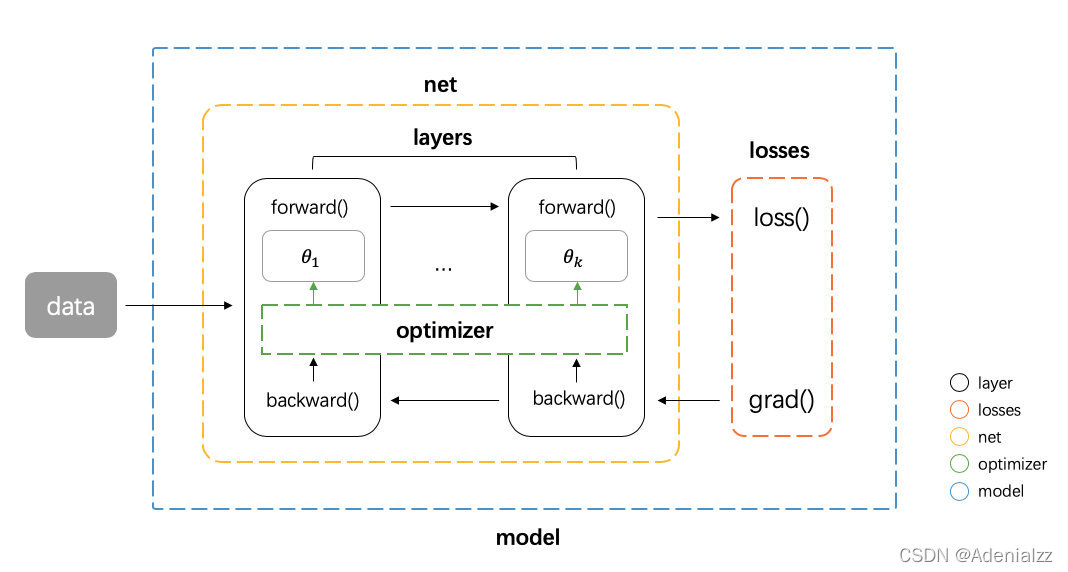
组件抽象

首先考虑神经网络运算的流程，神经网络运算主要包含训练 training 和预测 predict （或 inference） 两个阶段，

  • 训练的基本流程是：输入数据 -> 网络层前向传播 -> 计算损失 -> 网络层反向传播梯度 -> 更新参数；
  • 预测的基本流程是 输入数据 -> 网络层前向传播 -> 输出结果。

从运算的角度看，主要可以分为三种类型的计算：

  1. 数据在网络层直接的流动

    前向传播和反向传播可以看做是张量 Tensor（多维数组）在网络层之间的流动（前向传播流动的是输入输出，反向传播流动的是梯度），每个网络层会进行一定的运算，然后将结果输入给下一层。

  2. 计算损失

    衔接前向和反向传播的中间过程，定义了模型的输出与真实值之间的差异，用来后续提供反向传播所需的信息

  3. 参数更新

    使用计算得到的梯度对网络参数进行更新的一类计算

基于这个三种类型，我们可以对网络的基本组件做一个抽象

  • tensor 张量，这个是神经网络中数据的基本单位
  • layer 网络层，负责接收上一层的输入，进行该层的运算，将结果输出给下一层，由于 tensor 的流动有前向和反向两个方向，因此对于每种类型网络层我们都需要同时实现 forward 和 backward 两种运算
  • loss 损失，在给定模型预测值与真实值之后，该组件输出损失值以及关于最后一层的梯度（用于梯度回传）
  • optimizer 优化器，负责使用梯度更新模型的参数

然后我们还需要一些组件把上面这个 4 种基本组件整合到一起，形成一个 pipeline

  • net 组件负责管理 tensor 在 layer 之间的前向和反向传播，同时能提供获取参数、设置参数、获取梯度的接口
  • model 组件负责整合所有组件，形成整个 pipeline。即 net 组件进行前向传播 -> loss 组件计算损失和梯度 -> net 组件将梯度反向传播 -> optimizer 组件将梯度更新到参数。

基本框架如下图

在这里插入图片描述

组件实现

按照上面的抽象，我们可以写出整个流程代码如下。首先定义 net，net 的输入是多个网络层，然后将 net、loss、optimizer 一起传给 model。model 实现了 forward、backward 和 apply_grad 三个接口分别对应前向传播、反向传播和参数更新三个功能。

# define model
net = Net([layer1, layer2, ...])
model = Model(net, loss_fn, optimizer)

# training
pred = model.forward(train_X)
loss, grads = model.backward(pred, train_Y)
model.apply_grad(grads)

# inference
test_pred = model.forward(test_X)

接下来我们看这里边各个部分分别如何实现。

  • tensor

    tensor 张量是神经网络中基本的数据单位，我们这里直接使用 numpy.ndarray 类作为 tensor 类的实现（numpy 底层使用了 C 和 Fortran，并且在算法层面进行了大量的优化，运算速度也不算慢）

  • layer

    上面流程代码中 model 进行 forward 和 backward，其实底层都是网络层在进行实际运算，因此网络层需要有提供 forward 和 backward 接口进行对应的运算。同时还应该将该层的参数和梯度记录下来。先实现一个基类如下

    # layer.py
class Layer(object):
    def __init__(self, name):
        self.name = name
        self.params, self.grads = None, None

    def forward(self, inputs):
        raise NotImplementedError

    def backward(self, grad):
        raise NotImplementedError

    最基础的一种网络层是全连接网络层，实现如下。forward 方法接收上层的输入 inputs，实现 w x + b wx+b wx+b 的运算；backward 的方法接收来自上层的梯度，计算关于参数 w , b w,b w,b 和输入的梯度，然后返回关于输入的梯度。这三个梯度的推导可以见附录，这里直接给出实现。w_init 和 b_init 分别是参数 weight 和 bias 的初始化器，这个我们在另外的一个实现初始化器中文件 initializer.py 去实现，这部分不是核心部件，所以在这里不展开介绍。

    # layer.py
class Dense(Layer):
    def __init__(self, num_in, num_out,
                 w_init=XavierUniformInit(),
                 b_init=ZerosInit()):
        super().__init__("Linear")

        self.params = {
            "w": w_init([num_in, num_out]),
            "b": b_init([1, num_out])}

        self.inputs = None

    def forward(self, inputs):
        self.inputs = inputs
        return inputs @ self.params["w"] + self.params["b"]

    def backward(self, grad):
        self.grads["w"] = self.inputs.T @ grad
        self.grads["b"] = np.sum(grad, axis=0)
        return grad @ self.params["w"].T

    同时神经网络中的另一个重要的部分是激活函数。激活函数可以看做是一种网络层，同样需要实现 forward 和 backward 方法。我们通过继承 Layer 类实现激活函数类，这里实现了最常用的 ReLU 激活函数。func 和 derivation_func 方法分别实现对应激活函数的正向计算和梯度计算。

    # layer.py
class Activation(Layer):
		"""Base activation layer"""
    def __init__(self, name):
        super().__init__(name)
        self.inputs = None

    def forward(self, inputs):
        self.inputs = inputs
        return self.func(inputs)

    def backward(self, grad):
        return self.derivative_func(self.inputs) * grad

    def func(self, x):
        raise NotImplementedError

    def derivative_func(self, x):
        raise NotImplementedError

class ReLU(Activation):
		"""ReLU activation function"""
    def __init__(self):
        super().__init__("ReLU")

    def func(self, x):
        return np.maximum(x, 0.0)

    def derivative_func(self, x):
        return x > 0.0

  • net

    上文提到 net 类负责管理 tensor 在 layer 之间的前向和反向传播。forward 方法很简单，按顺序遍历所有层，每层计算的输出作为下一层的输入；backward 则逆序遍历所有层，将每层的梯度作为下一层的输入。这里我们还将每个网络层参数的梯度保存下来返回，后面参数更新需要用到。另外 net 类还实现了获取参数、设置参数、获取梯度的接口，也是后面参数更新时需要用到

    # net.py
class Net(object):
    def __init__(self, layers):
        self.layers = layers

    def forward(self, inputs):
        for layer in self.layers:
            inputs = layer.forward(inputs)
        return inputs

    def backward(self, grad):
        all_grads = []
        for layer in reversed(self.layers):
            grad = layer.backward(grad)
            all_grads.append(layer.grads)
        return all_grads[::-1]

    def get_params_and_grads(self):
        for layer in self.layers:
            yield layer.params, layer.grads

    def get_parameters(self):
        return [layer.params for layer in self.layers]

    def set_parameters(self, params):
        for i, layer in enumerate(self.layers):
            for key in layer.params.keys():
                layer.params[key] = params[i][key]

  • loss

    上文我们提到 loss 组件需要做两件事情，给定了预测值和真实值，需要计算损失值和关于预测值的梯度。我们分别实现为 loss 和 grad 两个方法，这里我们实现多分类回归常用的 SoftmaxCrossEntropyLoss 损失。这个的损失 loss 和梯度 grad 的计算公式推导进文末附录，这里直接给出结果：

    多分类 softmax 交叉熵的损失为
    J C E ( y , y ^ ) = − ∑ i = 1 N l o g   y ^ i c J_{CE}(y,\hat{y})=-\sum_{i=1}^Nlog\ \hat{y}_i^c JCE​(y,y^​)=−i=1∑N​log y^​ic​
    梯度稍微复杂一点，目标类别和非目标类别的计算公式不同。对于目标类别维度，其梯度为对应维度模型输出概率减一，对于非目标类别维度，其梯度为对应维度输出概率本身。
    ∂ J C E ∂ o c = { ( y ^ c − 1 ) / N      目标类别 c y c ~ / N                非目标类别 c ~ \frac{\partial{J_{CE}}}{\partial{o^c}}=\begin{cases} (\hat{y}^c-1)/N\ \ \ \ \ 目标类别c\\ y^{\tilde{c}}/N\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 非目标类别\tilde{c}\end{cases} ∂oc∂JCE​​={(y^​c−1)/N     目标类别cyc~/N               非目标类别c~​

    代码实现如下

    # loss.py
class BaseLoss(object):
    def loss(self, predicted, actual):
        raise NotImplementedError

    def grad(self, predicted, actual):
        raise NotImplementedError

class CrossEntropyLoss(BaseLoss):
  	def loss(self, predicted, actual):
        m = predicted.shape[0]
        exps = np.exp(predicted - np.max(predicted, axis=1, keepdims=True))
        p = exps / np.sum(exps, axis=1, keepdims=True)
        nll = -np.log(np.sum(p * actual, axis=1))
        return np.sum(nll) / m

    def grad(self, predicted, actual):
        m = predicted.shape[0]
        grad = np.copy(predicted)
        grad -= actual
        return grad / m

  • optimizer

    optimizer 主要实现一个接口 compute_step，这个方法根据当前的梯度，计算返回实际优化时每个参数改变的步长。我们在这里实现常用的 Adam 优化器。

    # optimizer.py
class BaseOptimizer(object):
    def __init__(self, lr, weight_decay):
        self.lr = lr
        self.weight_decay = weight_decay

    def compute_step(self, grads, params):
        step = list()
        # flatten all gradients
        flatten_grads = np.concatenate(
            [np.ravel(v) for grad in grads for v in grad.values()])
        # compute step
        flatten_step = self._compute_step(flatten_grads)
        # reshape gradients
        p = 0
        for param in params:
            layer = dict()
            for k, v in param.items():
                block = np.prod(v.shape)
                _step = flatten_step[p:p+block].reshape(v.shape)
                _step -= self.weight_decay * v
                layer[k] = _step
                p += block
            step.append(layer)
        return step

    def _compute_step(self, grad):
        raise NotImplementedError

class Adam(BaseOptimizer):
    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999,
                 eps=1e-8, weight_decay=0.0):
        super().__init__(lr, weight_decay)
        self._b1, self._b2 = beta1, beta2
        self._eps = eps

        self._t = 0
        self._m, self._v = 0, 0

    def _compute_step(self, grad):
        self._t += 1
        self._m = self._b1 * self._m + (1 - self._b1) * grad
        self._v = self._b2 * self._v + (1 - self._b2) * (grad ** 2)
        # bias correction
        _m = self._m / (1 - self._b1 ** self._t)
        _v = self._v / (1 - self._b2 ** self._t)
        return -self.lr * _m / (_v ** 0.5 + self._eps)

  • model

    最后 model 类实现了我们一开始设计的三个接口 forward、backward 和 apply_grad ，forward 直接调用 net 的 forward ，backward 中把 net 、loss、optimizer 串起来，先计算损失 loss，然后反向传播得到梯度，然后 optimizer 计算步长，最后由 apply_grad 对参数进行更新

    # model.py
class Model(object):
    def __init__(self, net, loss, optimizer):
        self.net = net
        self.loss = loss
        self.optimizer = optimizer

    def forward(self, inputs):
        return self.net.forward(inputs)

    def backward(self, preds, targets):
        loss = self.loss.loss(preds, targets)
        grad = self.loss.grad(preds, targets)
        grads = self.net.backward(grad)
        params = self.net.get_parameters()
        step = self.optimizer.compute_step(grads, params)
        return loss, step

    def apply_grad(self, grads):
        for grad, (param, _) in zip(grads, self.net.get_params_and_grads()):
            for k, v in param.items():
                param[k] += grad[k]

整体结构

最后我们实现出来核心代码部分文件结构如下：

tinynn
├── core
│   ├── __init__.py
│   ├── initializer.py
│   ├── layer.py
│   ├── loss.py
│   ├── model.py
│   ├── net.py
│   └── optimizer.py

其中 initializer.py 这个模块上面没有展开讲，主要实现了常见的参数初始化方法，用于给网络层初始化参数。

MNIST例子

框架基本搭起来后，我们找一个例子来用 tinynn 这个框架 run 起来。这个例子的基本一些配置如下

  • 数据集：MNIST
  • 任务类型：多分类
  • 网络结构：三层全连接 INPUT(784) -> FC(400) -> FC(100) -> OUTPUT(10)，这个网络接收 ( N , 784 ) (N,784) (N,784) 的输入，其中 N N N 是每次输入的样本数， 784 784 784 是每张 ( 28 , 28 ) (28,28) (28,28) 的图像展平后的向量，输出维度为 ( N , 10 ) (N,10) (N,10) ，其中 N N N 是样本数， 10 10 10 是对应图片在 10 10 10 个类别上的概率
  • 激活函数：ReLU
  • 损失函数：SoftmaxCrossEntropy
  • optimizer：Adam(lr=1e-3)
  • batch_size：128
  • Num_epochs：20

这里我们忽略数据载入、预处理等一些准备代码，只把核心的网络结构定义和训练代码贴出来如下

# example/mnist/run.py
net = Net([
  Dense(784, 400),
  ReLU(),
  Dense(400, 100),
  ReLU(),
  Dense(100, 10)
])
model = Model(net=net, loss=SoftmaxCrossEntropyLoss(), optimizer=Adam(lr=args.lr))

iterator = BatchIterator(batch_size=args.batch_size)
evaluator = AccEvaluator()
for epoch in range(num_ep):
    for batch in iterator(train_x, train_y):
      	# training
        pred = model.forward(batch.inputs)
        loss, grads = model.backward(pred, batch.targets)
        model.apply_grad(grads)
    # evaluate every epoch
    test_pred = model.forward(test_x)
    test_pred_idx = np.argmax(test_pred, axis=1)
    test_y_idx = np.asarray(test_y)
    res = evaluator.evaluate(test_pred_idx, test_y_idx)
    print(res)

运行结果如下

# tinynn
Epoch 0 	 {'total_num': 10000, 'hit_num': 9658, 'accuracy': 0.9658}
Epoch 1 	 {'total_num': 10000, 'hit_num': 9740, 'accuracy': 0.974}
Epoch 2 	 {'total_num': 10000, 'hit_num': 9783, 'accuracy': 0.9783}
Epoch 3 	 {'total_num': 10000, 'hit_num': 9799, 'accuracy': 0.9799}
Epoch 4 	 {'total_num': 10000, 'hit_num': 9805, 'accuracy': 0.9805}
Epoch 5 	 {'total_num': 10000, 'hit_num': 9826, 'accuracy': 0.9826}
Epoch 6 	 {'total_num': 10000, 'hit_num': 9823, 'accuracy': 0.9823}
Epoch 7 	 {'total_num': 10000, 'hit_num': 9819, 'accuracy': 0.9819}
Epoch 8 	 {'total_num': 10000, 'hit_num': 9820, 'accuracy': 0.982}
Epoch 9 	 {'total_num': 10000, 'hit_num': 9838, 'accuracy': 0.9838}
Epoch 10 	 {'total_num': 10000, 'hit_num': 9825, 'accuracy': 0.9825}
Epoch 11 	 {'total_num': 10000, 'hit_num': 9810, 'accuracy': 0.981}
Epoch 12 	 {'total_num': 10000, 'hit_num': 9845, 'accuracy': 0.9845}
Epoch 13 	 {'total_num': 10000, 'hit_num': 9845, 'accuracy': 0.9845}
Epoch 14 	 {'total_num': 10000, 'hit_num': 9835, 'accuracy': 0.9835}
Epoch 15 	 {'total_num': 10000, 'hit_num': 9817, 'accuracy': 0.9817}
Epoch 16 	 {'total_num': 10000, 'hit_num': 9815, 'accuracy': 0.9815}
Epoch 17 	 {'total_num': 10000, 'hit_num': 9835, 'accuracy': 0.9835}
Epoch 18 	 {'total_num': 10000, 'hit_num': 9826, 'accuracy': 0.9826}
Epoch 19 	 {'total_num': 10000, 'hit_num': 9819, 'accuracy': 0.9819}

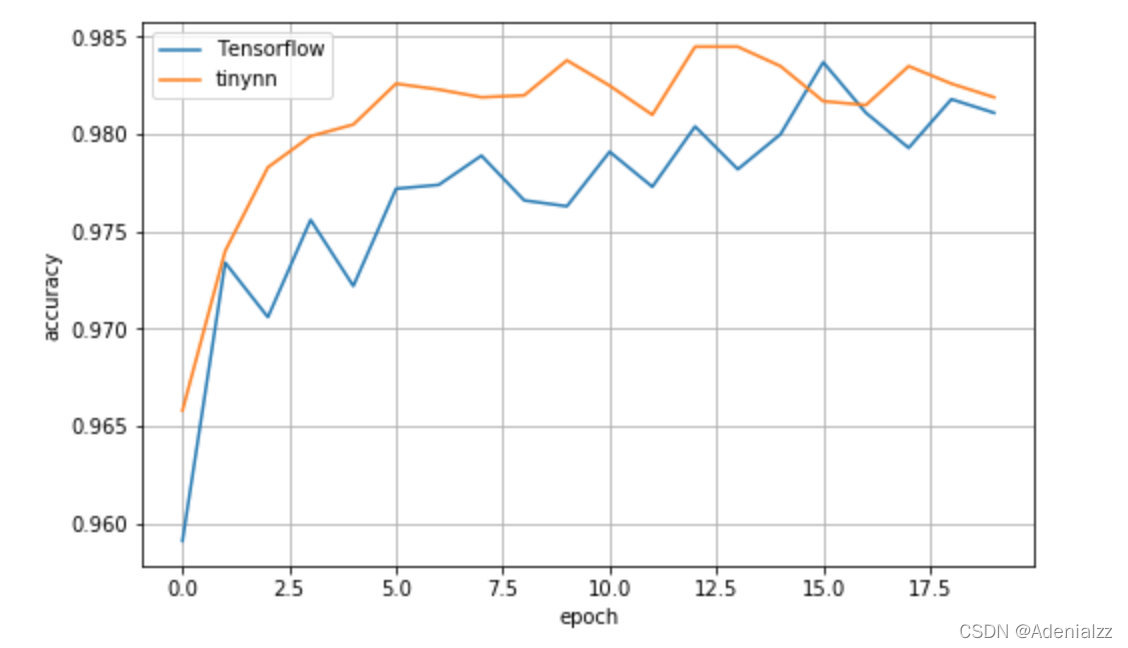
可以看到测试集 accuracy 随着训练进行在慢慢提升，这说明数据在框架中确实按照正确的方式进行流动和计算。为了对比下效果，我用 Tensorflow (1.13.1) 实现了相同的网络结构、采用相同的采数初始化方法、优化器配置等等，得到的结果如下

# Tensorflow 1.13.1
Epoch 0 	 {'total_num': 10000, 'hit_num': 9591, 'accuracy': 0.9591}
Epoch 1 	 {'total_num': 10000, 'hit_num': 9734, 'accuracy': 0.9734}
Epoch 2 	 {'total_num': 10000, 'hit_num': 9706, 'accuracy': 0.9706}
Epoch 3 	 {'total_num': 10000, 'hit_num': 9756, 'accuracy': 0.9756}
Epoch 4 	 {'total_num': 10000, 'hit_num': 9722, 'accuracy': 0.9722}
Epoch 5 	 {'total_num': 10000, 'hit_num': 9772, 'accuracy': 0.9772}
Epoch 6 	 {'total_num': 10000, 'hit_num': 9774, 'accuracy': 0.9774}
Epoch 7 	 {'total_num': 10000, 'hit_num': 9789, 'accuracy': 0.9789}
Epoch 8 	 {'total_num': 10000, 'hit_num': 9766, 'accuracy': 0.9766}
Epoch 9 	 {'total_num': 10000, 'hit_num': 9763, 'accuracy': 0.9763}
Epoch 10 	 {'total_num': 10000, 'hit_num': 9791, 'accuracy': 0.9791}
Epoch 11 	 {'total_num': 10000, 'hit_num': 9773, 'accuracy': 0.9773}
Epoch 12 	 {'total_num': 10000, 'hit_num': 9804, 'accuracy': 0.9804}
Epoch 13 	 {'total_num': 10000, 'hit_num': 9782, 'accuracy': 0.9782}
Epoch 14 	 {'total_num': 10000, 'hit_num': 9800, 'accuracy': 0.98}
Epoch 15 	 {'total_num': 10000, 'hit_num': 9837, 'accuracy': 0.9837}
Epoch 16 	 {'total_num': 10000, 'hit_num': 9811, 'accuracy': 0.9811}
Epoch 17 	 {'total_num': 10000, 'hit_num': 9793, 'accuracy': 0.9793}
Epoch 18 	 {'total_num': 10000, 'hit_num': 9818, 'accuracy': 0.9818}
Epoch 19 	 {'total_num': 10000, 'hit_num': 9811, 'accuracy': 0.9811}

在这里插入图片描述

可以看到 两者效果上大差不差，就单次的实验看比 Tensorflow 稍微好一点点。

总结

tinynn 相关的源代码在这个 repo 里。目前支持：

  • layer：全连接层、2D 卷积层、 2D 反卷积层、MaxPooling 层、Dropout 层、BatchNormalization 层、RNN 层以及 ReLU、Sigmoid、Tanh、LeakyReLU、SoftPlus 等激活函数
  • loss：SigmoidCrossEntropy、SoftmaxCrossEntroy、MSE、MAE、Huber
  • optimizer：RAam、Adam、SGD、RMSProp、Momentum 等优化器，并且增加了动态调节学习率 LRScheduler
  • 实现了 mnist（分类）、nn_paint（回归）、DQN（强化学习）、AutoEncoder 和 DCGAN （无监督）等常见模型。见 tinynn/examples

tinynn 还有很多可以继续完善的地方受限于时间还没有完成（实现循环神经网络层、BatchNorm 层、对运算效率进行优化等等），笔者在空闲时间会进行维护和更新。

当然从生产应用的角度 tinynn 可能是一个糟糕的选择，理由用 python 实现在这种计算密集型的场景中会不可避免地出现性能问题、没有 GPU 支持、没有分布式支持、很多算法还没实现等等等，这个小项目的出发点更多地是学习，在设计和实现 tinynn 的过程中笔者个人学习确实到了很多东西，包括如何抽象、如何设计组件接口、如何更效率的实现、算法的具体细节等等。对笔者而言这个写这个小框架除了了解深度学习框架的设计与实现之外还有一个好处：后续可以在这个框架上快速地实现一些新的算法，比如新出了某篇 paper 提出来新的参数初始化方法，新的优化算法，新的网络结构设计，都可以快速地在这个小框架上实验。

如果你对自己设计实现一个深度学习框架也感兴趣，希望看完这篇文章会对你有所帮助，也欢迎大家提 PR 一起贡献代码~

附录 Softmax 交叉熵损失和梯度推导

多分类下交叉熵损失如下式：
J C E ( y , y ^ ) = − ∑ i = 1 N ∑ k = 1 K y i k l o g   y i k ^ J_{CE}(y,\hat{y})=-\sum_{i=1}^N\sum_{k=1}^Ky_i^klog\ \hat{y_i^k} JCE​(y,y^​)=−i=1∑N​k=1∑K​yik​log yik​^​
其中 y , y ^ y,\hat{y} y,y^​ 分别是真实值和模型预测值， N N N 是样本数， K K K 是类别个数。由于真实值一般为一个 one-hot 向量（除了真实类别维度为 1 其他均为 0），因此上式可以化简为
J C E ( y , y ^ ) = − ∑ i = 1 N l o g   y i c ^ J_{CE}(y,\hat{y})=-\sum_{i=1}^Nlog\ \hat{y_i^c} JCE​(y,y^​)=−i=1∑N​log yic​^​
其中 c c c 是代表真实类别， y i c ^ \hat{y_i^c} yic​^​ 代表第 i i i 个样本 c c c 类的预测概率。即我们需要计算的是每个样本在真实类别上的预测概率的对数的和，然后再取负就是交叉熵损失。

接下来推导如何求解该损失关于模型输出的梯度，用 o o o 表示模型输出，在多分类中通常最后会使用 Softmax 将网络的输出归一化为一个概率分布，则 Softmax 后的输出为
y c ^ = e x p ( o c ) ∑ k = 1 K e x p ( o k ) \hat{y_c}=\frac{exp(o^c)}{\sum_{k=1}^Kexp(o^k)} yc​^​=∑k=1K​exp(ok)exp(oc)​
代入上面的损失函数
J C E = − ∑ i = 1 N ( o i c − l o g ∑ k = 1 K e x p ( o i k ) ) J_{CE}=-\sum_{i=1}^N(o_i^c-log\sum_{k=1}^Kexp(o_i^k)) JCE​=−i=1∑N​(oic​−logk=1∑K​exp(oik​))
求解 J C E J_{CE} JCE​ 关于输出向量 o o o 的梯度，可以将 o o o 分为目标类别所在维度 o c o^c oc 和非目标类别维度 KaTeX parse error: Got function '\tilde' with no arguments as superscript at position 3: o^\̲t̲i̲l̲d̲e̲{c}。首先看目标类别所在维度 o c o^c oc
∂ J C E ∂ o c = − ∑ i = 1 N ( 1 − e x p ( o c ) ∑ k = 1 K e x p ( o k ) ) = ∑ i = 1 N ( y ^ − 1 ) \frac{\partial{J_{CE}}}{\partial{o^c}}=-\sum_{i=1}^N(1-\frac{exp(o^c)}{\sum_{k=1}^Kexp(o^k)})=\sum_{i=1}^N(\hat{y}-1) ∂oc∂JCE​​=−i=1∑N​(1−∑k=1K​exp(ok)exp(oc)​)=i=1∑N​(y^​−1)
再看非目标类别所在维度 o c ~ o^{\tilde{c}} oc~
∂ J C E ∂ o c ~ = − ∑ i = 1 N ( − e x p ( o c ) ∑ k = 1 K e x p ( o k ) ) = ∑ i = 1 N ( y ^ ) \frac{\partial{J_{CE}}}{\partial{o^{\tilde{c}}}}=-\sum_{i=1}^N(-\frac{exp(o^c)}{\sum_{k=1}^Kexp(o^k)})=\sum_{i=1}^N(\hat{y}) ∂oc~∂JCE​​=−i=1∑N​(−∑k=1K​exp(ok)exp(oc)​)=i=1∑N​(y^​)
可以看到对于目标类别维度，其梯度为对应维度模型输出概率减一，对于非目标类别维度，其梯度为对应维度输出概率本身。

参考

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
java毕业生设计学生信息管理系统2021计算机源码+系统+mysql+调试部署+lw
循环神经网络RNN、LSTM、GRU实现股票预测
Qml-Behavior的使用
[SWPUCTF 2021 新生赛]gift_F12
java设计模式：03-04-装饰器模式
Java实现递归与回溯算法详解及图解
Linux命令cat＜＜EOF的使用
SpringBoot开发项目实战记录（未完结）
Lua Debug.GetInfo
paddleocr打包exe错误汇总
;