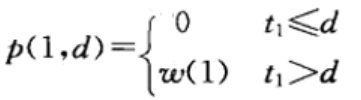问题描述：

动态规划+贪心思想：

（这题好像一般归类在贪心，但我感觉主要就是个动态规划）
1.首先将任务按其截止时间非减序排序。
2.对任务 1 , 2 , …… , i，如果截止时间为 d ，则最小误时惩罚为 p( i , d ) 。
3.对第一个任务来说：完成任务时间t<=任务截止时间，这个任务可以做完，没有惩罚时间；否则不做，有惩罚时间。

4.对于其他任务：
①如果任务时间t>任务截止时间，不能执行该任务。
p( i , d ) =p(i-1, d)+wi
②如果任务时间t<=任务截止时间，可以执行也可以不执行。
p( i , d ) = min{ p(i-1, d)+wi ， p(i-1, min{d, di}-ti) }
前者表示不执行任务，后者表示执行（这时必须在第 i 个任务的截至时间前做完它（即 min{d, di}-ti ））

代码：

#include <iostream>
#include <algorithm> 
using namespace std;
struct task{
	int t;//任务时间
	int d;//截止时间
	int w;//惩罚时间 
}; 
bool cmp(task x,task y)
{
	return x.d<y.d;
}
int main()
{
	int n;cin>>n;//输入任务个数
	task a[n+1];
	for(int i=1;i<=n;++i)
		cin>>a[i].t>>a[i].d>>a[i].w;
	sort(a+1,a+n+1,cmp); //按照截止时间非减排序 
	int p[n+1][n+1];
	/*处理第一个任务*/
	for(int i=0;i<=a[n].d;i++)
    {
        if(i<a[1].t) p[1][i]=a[1].w;//罚
        else p[1][i] = 0;//做第一个任务 
    }
    /*处理第2~n个任务*/
    for(int i=2;i<=n;++i)
		for(int j=0;j<=a[n].d;++j)
		{
			int x=p[i-1][j]+a[i].w;
			int y=p[i-1][min(j, a[i].d)-a[i].t];
			if (j<a[i].t) p[i][j]=x;//当前任务无法做 
			else p[i][j]=min(x,y);//可做可不做，选最优 
   		 }
	cout<<p[n][a[n].d]<<endl;
	return 0;
}

回溯法思路：

1.首先将任务按其截止时间非减序排序。
2.解空间可以用子集树表示。一共n个任务，节点左子树表示这个任务做，右子树不做。
3.变量t：当前所有做了的任务时间之和。
变量w：当前惩罚时间和。
变量bestw：记录最短的惩罚时间。
4.约束条件：t<=di(总时间t<=当前任务截止时间)，否则剪枝。
限界函数：w<=bestw(当前惩罚时间一定要小于最优惩罚时间)，否则没有继续dfs的必要，直接剪枝。

回溯法代码：

#include <iostream>
using namespace std;
int n;//任务个数 
struct task{
	int t;//任务时间
	int d;//截止时间
	int w;//惩罚时间 
}; 
task a[100];
int bestw;//存储最短的任务惩罚时间
int w;//当前的任务惩罚时间
int t;//当前所做任务总时间 
int x[100]; 

void backtrack(int i)
{
	if(i>n)//到达叶节点 
	{bestw=w;return;} 
	/*约束条件：所做任务总时间是否<=当前任务截止时间，成立进入左子树*/
	if(t+a[i].t<=a[i].d) 
	{	
		t+=a[i].t;//更新总时间 
		backtrack(i+1);
		t-=a[i].t;//回溯结束时时间要还原 
	} 
	/*限界函数：当前总惩罚是否<=bestw，成立进入右子树，否则剪枝*/ 
	if(w+a[i].w<=bestw) 
	{
		w=w+a[i].w;
		backtrack(i+1);
		w=w-a[i].w;
	}
}
int main()
{
	cin>>n;//输入任务个数
	w=0;t=0;bestw=1000;//先将bestw设置为一个较大的值 
	for(int i=1;i<=n;++i)
		cin>>a[i].t>>a[i].d>>a[i].w;
	backtrack(1);
	cout<<bestw<<endl;
	return 0; 
}