多臂老*虎*机问题

多臂老虎机问题

代码位于我本人的GitHub
本实验跟随bilibili-多臂老虎机问题视频介绍

1. 简介

多臂老虎机问题是概率论中一个经典问题,也属于强化学习的范畴.设想,一个赌徒面前有N个老虎机,事先他不知道每台老虎机的真实盈利情况,他如何根据每次玩老虎机的结果来选择下次拉哪台或者是否停止赌博,来最大化自己的从头到尾的收益.
关于多臂老虎机问题名字的来源,是因为老虎机在以前是有一个操控杆,就像一只手臂(arm),而玩老虎机的结果往往是口袋被掏空,就像遇到了土匪(bandit)一样,而在多臂老虎机问题中,我们面对的是多个老虎机.

来源: 知乎-多臂老虎机问题 https://zhuanlan.zhihu.com/p/84140092

2. 问题建模(简化版)

为了模拟现实环境，我们假设有两台老虎机，标记为A和B
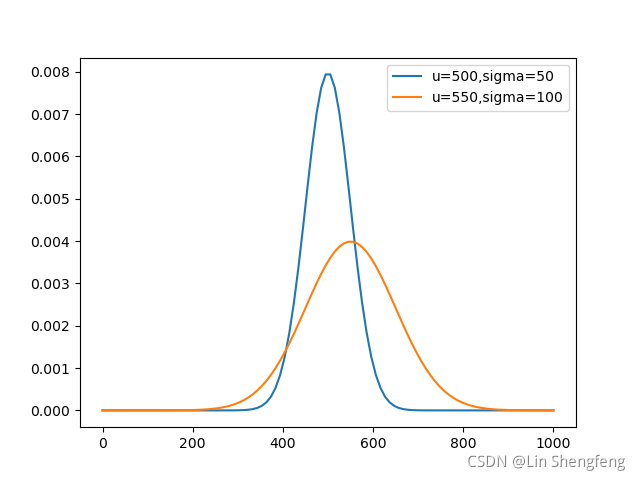
假设A的收益概率分布为µ(均值) = 500，σ(标准差) = 50的正态分布:
$N_A(\mu=500,\sigma=50)$
假设B的收益概率分布为µ(均值) = 550，σ(标准差) = 100的正态分布:
$N_B(\mu=550,\sigma=100)$
两者的概率分布图像如下:

概率分布图像

注意: 老虎机的收益概率分布对玩家是不可知的, 玩家只能通过不断尝试来逼近它们

每一轮游戏只能选择一台老虎机进行抽奖, 我们的目标是要让收益最大化.

3. 策略介绍

我们的思路是为每台老虎机保存一个Reward列表, 把从该老虎机每次获得的收益都加入到其对应的Reward列表. 对于每一台老虎机的Reward列表, 我们计算它的Q值(行动价值估计值, 马上会讲到怎么计算).在下一轮游戏时,利用贪婪(Greedy)策略选取Q值最高的老虎机.

# 初始化时认定第1台是收益最高的
max_Q = calculate_Q(bandits[0])  # maxQ表示当前最大的Q值
index_maxQ = 0  # index_maxQ表示老虎机序号
for i in len(bandits):  # 假设有一个存放Reward列表的列表bandits
  cur_Q = calculate_Q(bandits[i])  # 计算它的Q值
  if cur_Q >= max_Q:  # Greedy 贪婪策略
    max_Q = cur_Q  # 更新最大Q值
    index_maxQ = i  # 更新序号

上述伪代码介绍了如何利用贪婪策略选取老虎机.(因为本次只有两个老虎机,所以我的代码中直接用A和B来表示两台老虎机,并且手动比较,不涉及这段遍历比较的代码)

3.1 Q值(行动价值估计值)计算

Q值是衡量一台老虎机收益的指标, 其计算方法比较简单, 即求老虎机收益序列(即Reward序列)的平均值:
${\Sigma~Reward_a \over len(Reward_a)},a是老虎机序号$
也可以用另一个思路理解: t时刻某老虎机a的Q值,是之前选择该老虎机获得的总收益除以选择它的次数,公式中1(Ai = a)表示i时刻的动作(也就是选择的老虎机)如果是a则标记为1,否则为0.
$Q_t(a)= {\Sigma_{i=1}^{t-1}R_i*1(A_i=a) \over \Sigma_{i=1}^{t-1}1(A_i=a)},a是老虎机序号$
其计算代码如下:

def getQ(Reward, first=True):  # 也可以叫calculate_Q, 第二个参数first的含义会在3.2详细解释
    """
    :param Reward: 反馈序列
    :param first: 初始值是否参与计算, 默认True, 即参与
    :return: 该序列的Q值
    """
    if first:  # 带初始值计算
        return np.mean(Reward)  # 直接返回平均值即可
    else:  # 不带初始值计算
        if len(Reward) == 1:  # 目前Reward序列中只有初始值  
            return Reward[0]  # 那就只能返回初始值
        else:  # 有很多值了
            return sum([Reward[i] for i in range(1, len(Reward))])//(len(Reward) - 1)  # 计算除去初始值的序列平均值

3.2 初始值设置

假设我们还没有开始玩老虎机, 如果我们不往它们各自的Reward序列中添加一个合适的数值, 试想一下会发生什么.

例如, t=0时刻, A和B目前各自的Q值都为0, 然后因为它们的Q值相同, 我们选择了B, 然后获得了收益(假设的)100. 于是在t=1时刻, 我们发现A的Q值为0, B的Q值为100, 然后接下来依然选择B. 根据贪婪的策略, 我们永远也不会选择到A.

为了克服这个问题, 我们可以适当向每台老虎机的Reward序列中加入一个初始值, 并且这个初始值要足够大.

那么根据我们在 2中设置的概率分布, 我们可以加入初始值998(可以改,但一定要足够大). 初始值可以选择加入到Q值计算, 也可以选择不加入. 3.1中的Q函数默认带上初始值计算. 如果不带初始值计算, 那么在序列中只有初始值情况时, 我们返回初始值, 其余情况返回不含初始值的序列平均值.

现在我们看看跟没加初始值相比,发生了什么样的变化:

t=0时刻, A和B目前各自的Q值都为998, 然后因为它们的Q值相同, 我们选择了B, 然后获得了收益(假设的)100. 于是在t=1时刻, 我们发现A的Q值为998, B的Q值为549(默认带初始值), 根据贪婪的策略, 我们选择A!

3.3 鼓励探索, 弱化贪婪 `ξ-Greedy`

考虑到每台机器的随机性, 我们其实并不能保证选择到了最优的机器, 有时候期望收益最大的机器可能会表现得不尽人意.

这个时候, 我们就需要鼓励探索, 即不选择看似收益最大的那一台机器.

这就是ξ-Greedy(epsilon-Greedy)策略.

在本例子中, 假设t时刻我们计算出B的Q值更高, 但是我们以一定的概率选择A.

这个概率可以人为设定, 我假定为0.3

def pickHigherOne():
    """
    r取值在[1, 10]
    0.3 的概率不取Q值更高者
    :return:
        r <= 3:False
        3 <= r <= 10:True
    """
    r = random.randint(1, 10)  # 额非常粗糙的随机法, 将就一下.
    if r <= 3:
        return False
    else:
        return True

4.模拟及试验结果

4.1 模拟过程代码

假设我们总共玩20次老虎机. 主程序main.py如下:

from utils import *  # 这是我自己写的包, 会在下面附上

if __name__ == '__main__':
    # 我们的目标是从有限的步骤中尽量最大化自己的收益
    A = getNormRvs(500, 50, 20)  # 老虎机 A 的概率分布 N(500, 50), 假设取20步
    B = getNormRvs(550, 100, 20)  # 老虎机 B 的概率分布 N(550, 100), 假设取20步

    Reward_A = [998]  # 存放从 A 获得的奖励, 假设有初值998(初值设置很大是为了避免只能选一个的尴尬情况, 可以选择参与Q值计算)
    Reward_B = [998]  # 存放从 B 获得的奖励, 假设有初值998(初值设置很大是为了避免只能选一个的尴尬情况, 可以选择参与Q值计算)

    # ξ-Greedy, 假设 ξ = 0.3
    for i in range(20):  # 在有限的步数之内，每一步都做个决策, 决策的策略是使用Q值更大的那个，但是保持一定的概率会选取另一个
        Q_A = getQ(Reward_A, False)  # Reward_A 目前的Q值, 不带初值计算
        Q_B = getQ(Reward_B, False)  # Reward_B 目前的Q值, 不带初值计算
        print('老虎机A的Q值:{0}   老虎机B的Q值:{1}'.format(Q_A, Q_B))
        if Q_A == 998:  # 998 那肯定得先用它
            print_step_info(i, 'A', A[i], Reward_A, Q_A)

        elif Q_B == 998:  # 998 那肯定得先用它
            print_step_info(i, 'B', B[i], Reward_B, Q_B)

        else:
            pick_higher = pickHigherOne()
            if Q_A >= Q_B:  # Q_A 其实是要选择 A 的, 但因为 ξ, 所以可能会选B
                if pick_higher:  # 我们要选择更高的那个
                    print_step_info(i, 'A', A[i], Reward_A, Q_A)
                else:
                    print_step_info(i, 'B', B[i], Reward_B, Q_B)
            else:
                if pick_higher:  # 我们要选择更高的那个
                    print_step_info(i, 'B', B[i], Reward_B, Q_B)
                else:
                    print_step_info(i, 'A', A[i], Reward_A, Q_A)

utils.py内容如下:

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
import random
import time


def getNormRvs(mu, sigma, step):
    """
    :param mu: int, 正态分布的平均值
    :param sigma: int, 正态分布的标准差
    :param step: int, 从这个正态分布中随机取多少个值
    :return: 返回取出来的值序列(四舍五入取整, 因为假设真实情况下老虎机给的Reward是整数)
    """
    rvs = stats.norm.rvs(loc=mu, scale=sigma, size=step)
    return [int(0.5 + data) for data in rvs]


def getQ(Reward, first=True):  # 也可以叫calculate_Q, 第二个参数first的含义会在3.2详细解释
    """
    :param Reward: 反馈序列
    :param first: 初始值是否参与计算, 默认True, 即参与
    :return: 该序列的Q值
    """
    if first:  # 带初始值计算
        return np.mean(Reward)  # 直接返回平均值即可
    else:  # 不带初始值计算
        if len(Reward) == 1:  # 目前Reward序列中只有初始值
            return Reward[0]  # 那就只能返回初始值
        else:  # 有很多值了
            return sum([Reward[i] for i in range(1, len(Reward))])//(len(Reward) - 1)  # 计算除去初始值的序列平均值


def pickHigherOne():
    """
    r取值在[1, 10]
    0.3 的概率不取Q值更高者
    :return:
        r <= 3:False
        3 <= r <= 10:True
    """
    r = random.randint(1, 10)
    if r <= 3:
        return False
    else:
        return True


def print_step_info(step, name, rewardValue, rewardSeq, curQ):
    """
    :param step: 当前第step步
    :param name: 老虎机名称
    :param rewardValue: 老虎机提供的反馈值
    :param rewardSeq: 之前的反馈序列
    :return: 无返回值
    """
    print('当前是第{0}次, 选择了老虎机 {1}, 它的Reward是{2}, 当前Q值为{3}'.format(step + 1, name, rewardValue, int(curQ + 0.5)))
    print('----------------------')
    rewardSeq.append(rewardValue)  # 顺便把reward存入序列
    time.sleep(1)  # 慢慢打印结果

4.2 实验结果

老虎机A的Q值:998 老虎机B的Q值:998
 当前是第1次, 选择了老虎机 A, 它的Reward是524, 当前Q值为998
  ----------------------
老虎机A的Q值:524 老虎机B的Q值:998
 当前是第2次, 选择了老虎机 B, 它的Reward是519, 当前Q值为998
  ----------------------
老虎机A的Q值:524 老虎机B的Q值:519
 当前是第3次, 选择了老虎机 A, 它的Reward是515, 当前Q值为524
  ----------------------
老虎机A的Q值:519 老虎机B的Q值:519
 当前是第4次, 选择了老虎机 A, 它的Reward是498, 当前Q值为519
  ----------------------
老虎机A的Q值:512 老虎机B的Q值:519
 当前是第5次, 选择了老虎机 B, 它的Reward是356, 当前Q值为519
  ----------------------
老虎机A的Q值:512 老虎机B的Q值:437
 当前是第6次, 选择了老虎机 B, 它的Reward是673, 当前Q值为437
  ----------------------
老虎机A的Q值:512 老虎机B的Q值:516
 当前是第7次, 选择了老虎机 B, 它的Reward是563, 当前Q值为516
  ----------------------
老虎机A的Q值:512 老虎机B的Q值:527
 当前是第8次, 选择了老虎机 B, 它的Reward是421, 当前Q值为527
  ----------------------
老虎机A的Q值:512 老虎机B的Q值:506
 当前是第9次, 选择了老虎机 B, 它的Reward是689, 当前Q值为506
  ----------------------
老虎机A的Q值:512 老虎机B的Q值:536
 当前是第10次, 选择了老虎机 A, 它的Reward是507, 当前Q值为512
  ----------------------
老虎机A的Q值:511 老虎机B的Q值:536
 当前是第11次, 选择了老虎机 B, 它的Reward是587, 当前Q值为536
  ----------------------
老虎机A的Q值:511 老虎机B的Q值:544
 当前是第12次, 选择了老虎机 A, 它的Reward是493, 当前Q值为511
  ----------------------
老虎机A的Q值:507 老虎机B的Q值:544
 当前是第13次, 选择了老虎机 B, 它的Reward是519, 当前Q值为544
  ----------------------
老虎机A的Q值:507 老虎机B的Q值:540
 当前是第14次, 选择了老虎机 B, 它的Reward是483, 当前Q值为540
----------------------
老虎机A的Q值:507 老虎机B的Q值:534
当前是第15次, 选择了老虎机 A, 它的Reward是568, 当前Q值为507
  ----------------------
老虎机A的Q值:517 老虎机B的Q值:534
 当前是第16次, 选择了老虎机 B, 它的Reward是624, 当前Q值为534
  ----------------------
老虎机A的Q值:517 老虎机B的Q值:543
 当前是第17次, 选择了老虎机 B, 它的Reward是360, 当前Q值为543
  ----------------------
老虎机A的Q值:517 老虎机B的Q值:526
 当前是第18次, 选择了老虎机 B, 它的Reward是343, 当前Q值为526
  ----------------------
老虎机A的Q值:517 老虎机B的Q值:511
 当前是第19次, 选择了老虎机 B, 它的Reward是542, 当前Q值为511
  ----------------------
老虎机A的Q值:517 老虎机B的Q值:513
 当前是第20次, 选择了老虎机 A, 它的Reward是458, 当前Q值为517
  ----------------------

5 相关提醒

赌博?达咩! 🙅‍♂️🙅‍♂️🙅‍♂️
十个赌徒九个输，倾家荡产不如猪

《中华人民共和国刑法》第三百零三条：“以营利为目的，聚众赌博或者以赌博为业的，处三年以下有期徒刑、拘役或者管制，并处罚金。
“开设赌场的，处五年以下有期徒刑、拘役或者管制，并处罚金；情节严重的，处五年以上十年以下有期徒刑，并处罚金。
“组织中华人民共和国公民参与国（境）外赌博，数额巨大或者有其他严重情节的，依照前款的规定处罚。”