交叉验证
对于一个模型进行评估，需要用没有训练过的数据来进行测试，常见的方法比如将数据分为训练集和测试集，他有两个缺点，一是选出的测试集与训练集高度依赖，二是训练的时候没有用到所有的可用的数据。为了避免这些缺陷，采用k-fold交叉验证。将数据分成k组，每次训练k-1个组，剩下的当作测试集，如此循环k次。

digits = datasets.load_digits()# 下载手写数据集
features = digits.data
target = digits.target
standardizer = StandardScaler()# 预处理，归一化
logit = LogisticRegression()# 逻辑回归
pipeline = make_pipeline(standardizer, logit)# 创建管道
kf = KFold(n_splits=10, shuffle=True, random_state=1)
cv_results = cross_val_score(pipeline,
                             features,
                             target,
                             cv=kf,
                             scoring="accuracy",
                             n_jobs=-1)# n_jobs是同时工作的cpu个数（-1代表全部）
print(cv_results.mean())

创建基线回归模型

boston = load_boston()
features, target = boston.data, boston.target

features_train, features_test, target_train, target_test = train_test_split(features, target, random_state=0)
dummy = DummyRegressor(strategy='mean')
dummy.fit(features_train, target_train)
print(dummy.score(features_test, target_test))

可以将上述结果与普通的线性回归对比，看二者的分数。
基线回归的分类模型
与随机的分类预测对比。注意分层的预测与训练集的目标向量的类比例成正比
以及归一化将在不同的类别之间随机统一地生成预测。

boston = load_iris()# 换成鸢尾花用于分类
features, target = boston.data, boston.target
features_train, features_test, target_train, target_test = train_test_split(features, target, random_state=0)
dummy = DummyClassifier(strategy='uniform', random_state=1)
dummy.fit(features_train, target_train)
print(dummy.score(features_test, target_test))

模型表现
常用accuracy、precision、recall和F1来表征模型的表现。
$$accuracy=\frac{TP+TN}{TP+TN+FP+FN}$$
T、F代表正确或错误，P、N代表积极或消极。然而数据常常是不平衡类，有时候模型仅仅靠accuracy不能预测任何东西。
而precision假设预测中有噪声，预测为积极可能为消极。
$$precision=\frac{TP}{TP+FP}$$
recall表征模型确定样本为积极的能力
$$recall=\frac{TP}{TP+FN}$$
F1是precision和recall的调和平均数
$$F_1=2\times \frac{precision\times recall}{precision+recall}$$
在cross_val_score中参数scoring选择即可。
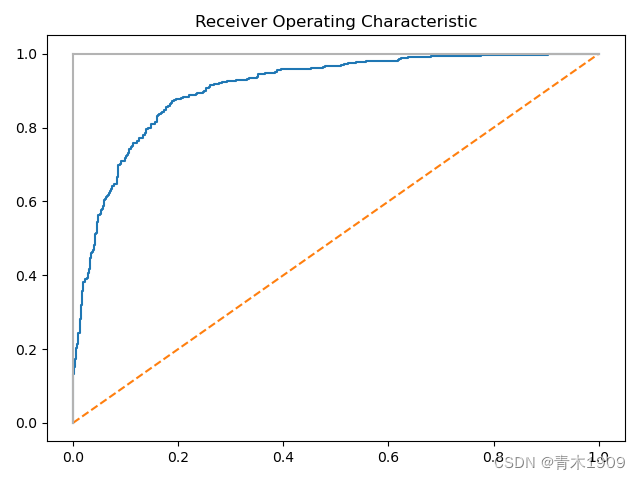
ROC曲线
预测每一个样本的分类情况，如果模型预测准确，则会迅速到达顶峰。

features, target = make_classification(n_samples=10000,
                                       n_features=10,
                                       n_classes=2,
                                       n_informative=3,
                                       random_state=3)

features_train, features_test, target_train, target_test = train_test_split(features, target, test_size=0.1, random_state=1)

logit = LogisticRegression()
logit.fit(features_train, target_train)

target_probabilities = logit.predict_proba(features_test)[:, 1]# 返回该标签的概率
false_positive_rate, true_positive_rate, threshold = roc_curve(target_test, target_probabilities)

plt.title("Receiver Operating Characteristic")
plt.plot(false_positive_rate, true_positive_rate)
plt.plot([0, 1], ls="--")
plt.plot([0, 0], [1, 0], c=".7"),plt.plot([1, 1], c=".7")
plt.show()

由于某些情况一个错误的阳性数据非常有用，于是有了TPR和FPR
$$TPR=\frac{TP}{TP+FN}$$
$$FPR=\frac{FP}{FP+TN}$$
ROC曲线则分别表示了TPR和FPR的每个样本的概率阈值。

多个类别的模型分类器评价
在类别大致均衡的条件下，可以使用accuracy，在不均衡条件下考虑其他例如recall、precision等。

features, target = make_classification(n_samples=10000,
                                       n_features=3,
                                       n_classes=3,
                                       n_informative=3,
                                       n_redundant=0,
                                       random_state=3)


logit = LogisticRegression()
print(cross_val_score(logit, features, target, scoring='accuracy'))

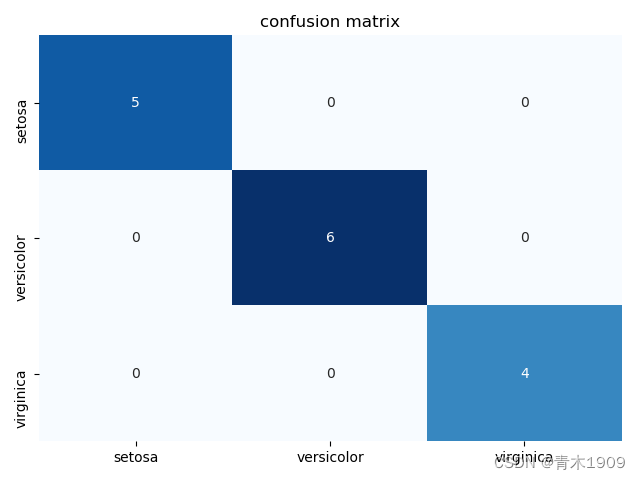
分类器性能可视化
列表示预测类别，行为真是类别

iris = datasets.load_iris()
features = iris.data
target = iris.target
class_names = iris.target_names
features_train, features_test, target_train, target_test = \
    train_test_split(features, target, test_size=0.1, random_state=1)
classifier = LogisticRegression()

target_predicted = classifier.fit(features_train, target_train).predict(features_test)

matrix = confusion_matrix(target_test, target_predicted)# 混淆矩阵产生
dataframe = pd.DataFrame(matrix, index=class_names, columns=class_names)
sns.heatmap(dataframe, annot=True, cbar=None, cmap='Blues')

plt.title("confusion matrix")
plt.tight_layout()
plt.show()

混淆矩阵可以看出分类器错了以及错在了哪里。
全部预测正确
评估回归模型
MSE是最常见的回归模型的评估
$$MSE=\frac{1}{n}\sum _{i=1}^n({\hat{y}}_i-y_i{)}^2$$
平方内部前者是预测值，后者是真实值。

features, target = make_regression(n_samples=100,
                                   n_features=3,
                                   n_informative=3,
                                   n_targets=1,
                                   noise=50,
                                   coef=False,
                                   random_state=1)

ols = LinearRegression()

print(cross_val_score(ols, features, target, scoring='neg_mean_squared_error'))
# 注意scoring的参数是由于sklearn默认高值由于低值

聚类模型评估
监督学习中聚类模型中最常见的问题在于数据没有目标向量，在没有目标向量的时候，我们假定同一个簇差距不大而不同簇差距较大。
我们使用轮廓指数，提供简单的测量指标。
$$s_i=\frac{b_i-a_i}{max(a_i,b_i)}$$,其中a是该样本和其他相同簇的平均距离，b是和最近的不同簇的平均距离。

silhouette_score(features, target_predicted)

自定义的评价指标
将r2包到自己定义的函数中。

from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Ridge
from sklearn.metrics import make_scorer, r2_score

features, target = make_regression(n_samples=100,
                                   n_features=3,
                                   random_state=1)

features_train, features_test, target_train, target_test = train_test_split(features, target, test_size=0.1, random_state=1)

def custom_metric(target_test, target_pridicted):
    r2 = r2_score(target_test, target_pridicted)
    return r2

score = make_scorer(custom_metric, greater_is_better=True)

clasifier = Ridge()

model = clasifier.fit(features_train, target_train)

print(score(model, features_test, target_test))