电路解题的第一步往往是化简。以下说明电路分析中的几个重要化简方法。
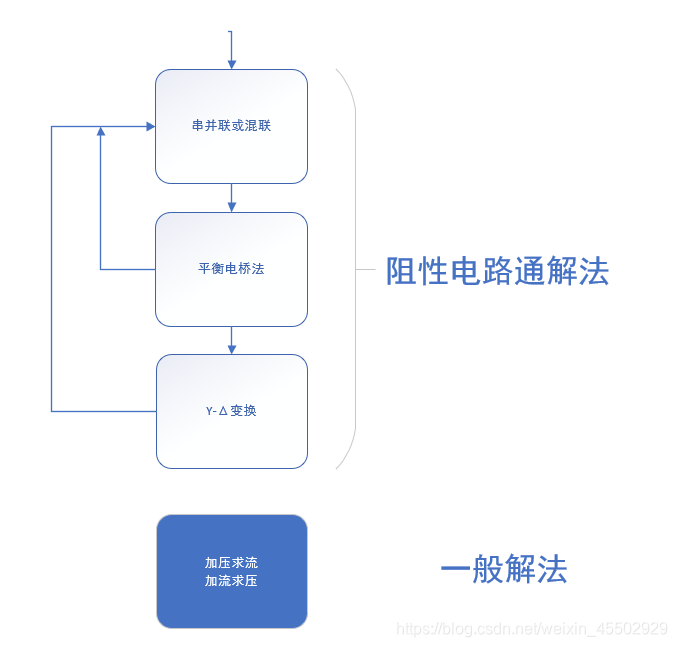
求解方法综述
电路分析中有很多典型而简单的分析方法,比如混联电路的分析、平衡电桥。但同时我们发现很多问题是不能简单地进行求解的,所以我们还要讨论一些网络等效的方法,包括网络的等效、电源等效,etc。
1. 电阻的串并联规律
1.1. 串联
对串联回路使用KVL,得到串联电阻的阻值:
R
s
=
∑
R
i
R_s=\sum R_i
Rs=∑Ri
由Ohm定律,串联分压规律:
U
i
R
i
=
U
s
R
s
\frac{U_i}{R_i}=\frac{U_s}{R_s}
RiUi=RsUs
- 对于一个非独立电压源,考虑电路中串入一个内电阻。由分压规律,这个电阻越小,那么负载电压越大。
1.2. 并联
对并联节点使用KCL,可得并联的电导:
G
p
=
∑
G
k
G_p=\sum G_k
Gp=∑Gk
由电导的Ohm定律,并联分流规律:
i
k
i
=
G
k
G
p
\frac{i_k}{i}=\frac{G_k}{G_p}
iik=GpGk
- 特别地,对于两个支路并联,支路电流占总电流比重等于对侧电阻占阻值之和的比重。
- 对一个非独立电流源,考虑电路中并入一个内电阻。由分流规律,这个电阻越大,那么负载电流越大。
1.3. 串并联简化方法( ∗ \ast ∗)
寻找直接串联或者并联在电源上的网络部分
这样的部分是一定存在的,只要是一个混连电路,最外层结构必然是一个串联或一个并联。
对其进行移动节点,或删除简化。对于一个确定的串并联混合电路,都可以通过这样的方法逐步实现问题的解析。
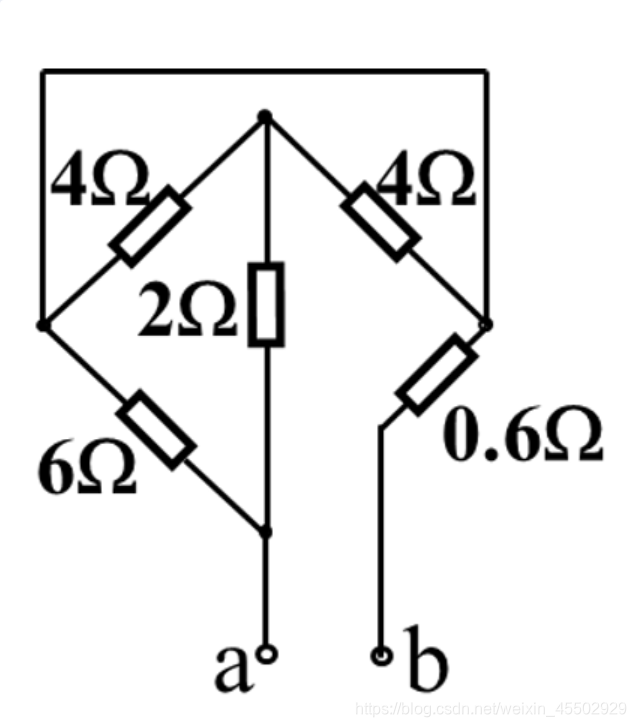
例题 求这个串并联网络的电阻:
- step 1:0.6串联
- step 2:6并联
- step 3:右边的4串联
- step 4:左边的4和2并联
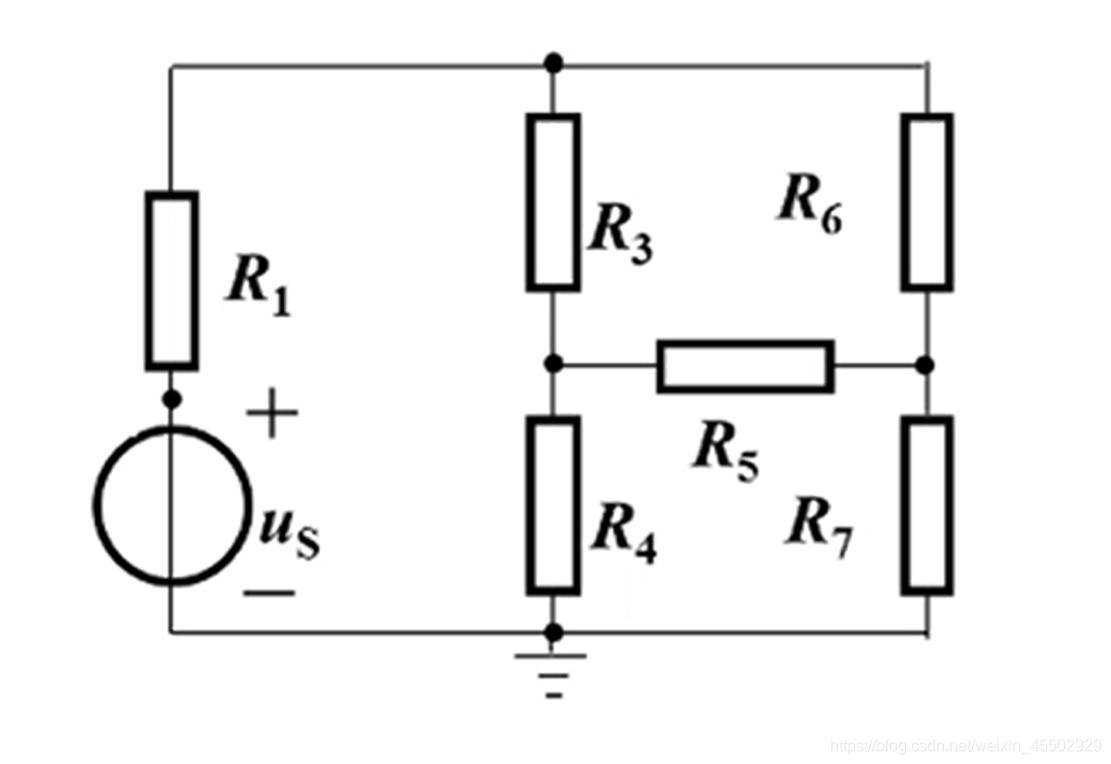
2. 电桥和平衡电桥
2.1 电桥的识别
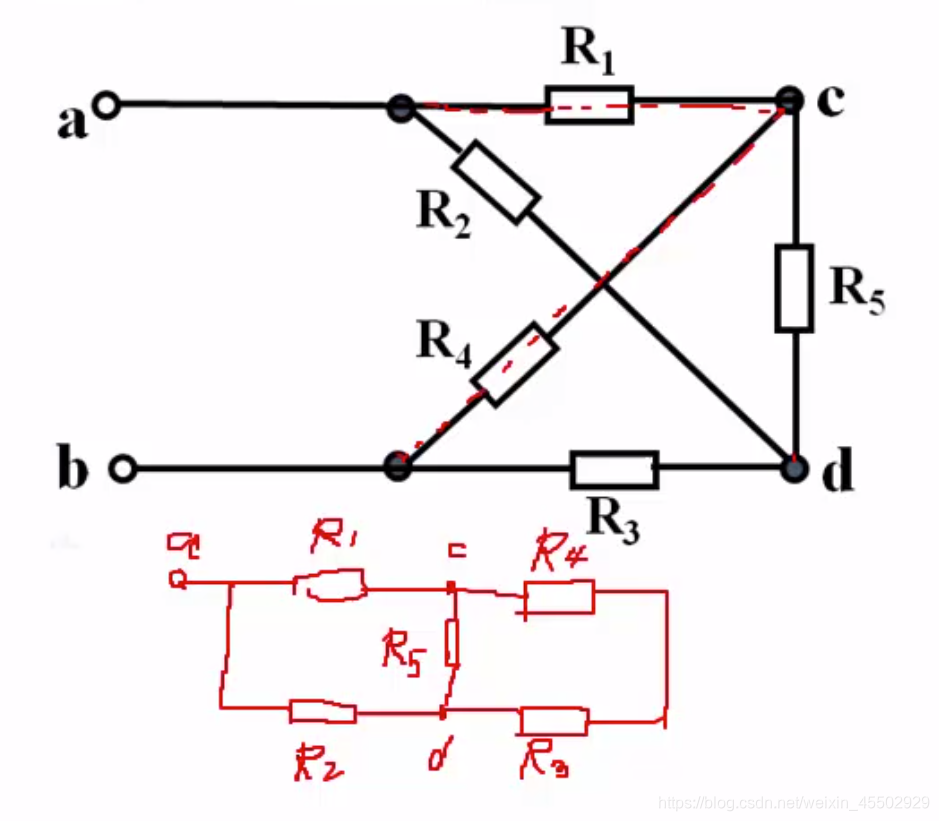
如图,交叉为变形电桥,电路哥手画的电路为标准电桥。
利用这个交叉电桥网络,来说明以下判据12345
1套电桥:
2条最短路径(acb和adb)
每个节点3条连线
4个元件参与分压
加上电桥5个元件
梳理两条最短路提纲挈领的纲!
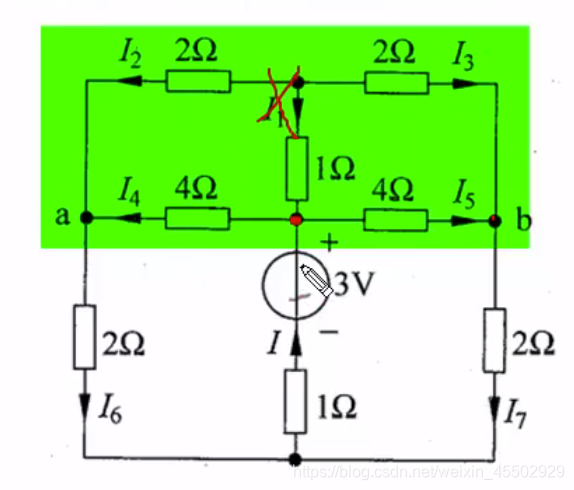
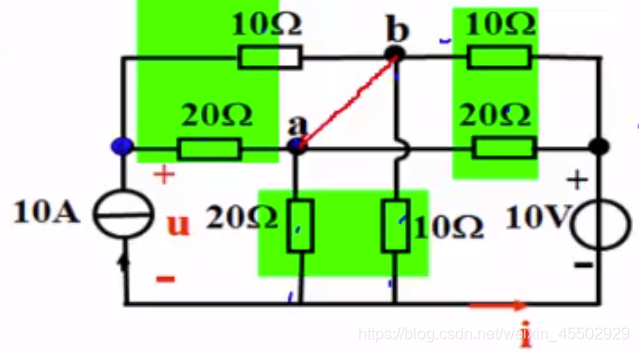
又比如如下绿色区域,形状接近但并不是电桥:
因为如图的红点上链接了四条线。
2.2 电桥平衡
由分压规律
U
A
=
R
2
R
1
+
R
2
U_A=\frac{R_2}{R_1+R_2}
UA=R1+R2R2
U
B
=
R
4
R
3
+
R
4
U_B=\frac{R_4}{R_3+R_4}
UB=R3+R4R4
如果
R
1
R
4
=
R
2
R
3
R_1R_4=R_2R_3
R1R4=R2R3,那么AB两点是等电位点。从而中间连入的电阻没有电流通过。因而这个平衡电桥简化为简单的串并联结构。
平衡电桥可以认为是并联的串联,也可以看成串联的并联。
应用:利用是否有电流,可以测定位置电阻的阻值。
2.3 电桥平衡的应用
电桥平衡主要帮助我们进行电路简化。当发现电路难以通过简单的串并联进行描述时,就要想到利用电桥了。
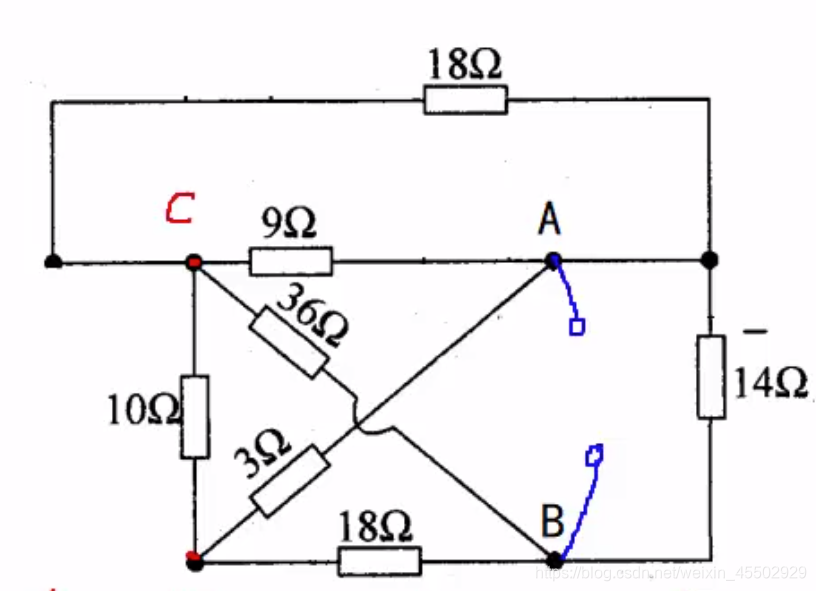
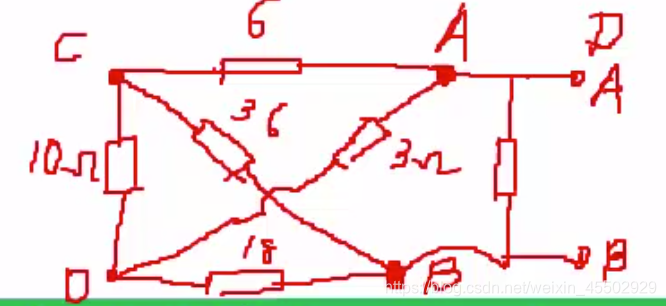
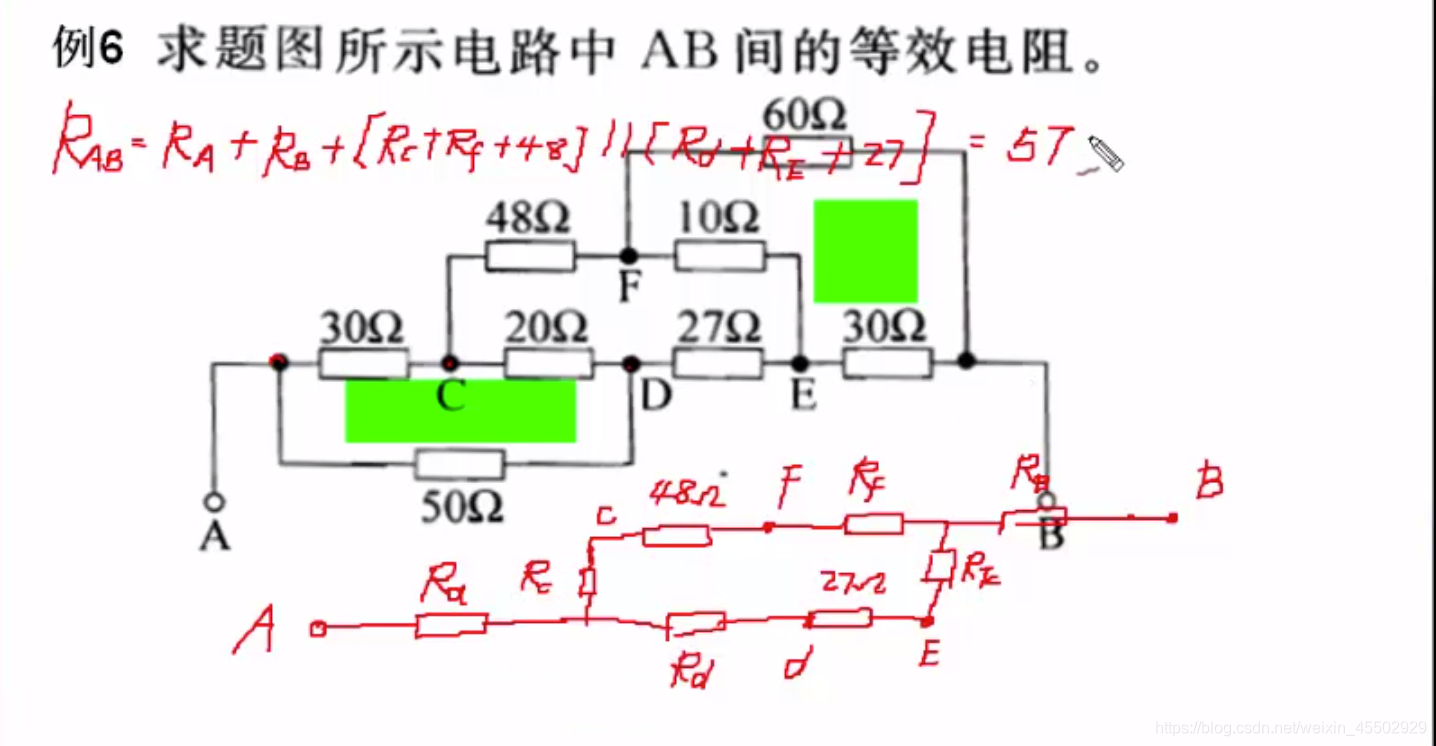
例1
如图,18Ω所在电路实际上也是一条最短路。将其中1/4个分压元件组(即那个9Ω电阻)进行并联,改造成标准型如图二。随后简化为平衡电桥。
2.4 平衡电桥的对称性
在平衡电桥上,加一个电压激励,则在电桥对外端口上电压为0
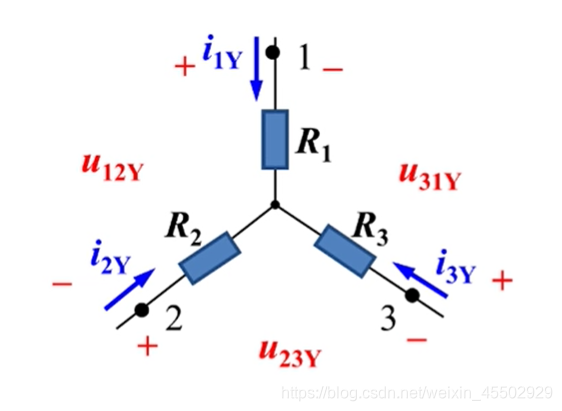
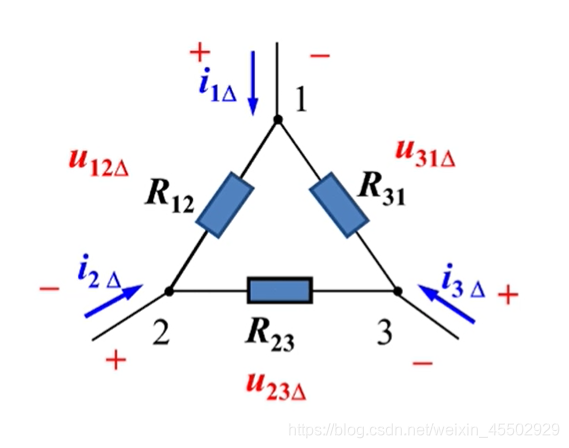
3. Y − Δ Y-\Delta Y−Δ(星-三角变换):三角形网络
3.1. Y − T Y-T Y−T和 Δ − Π \Delta-\Pi Δ−Π形
前者是三分岔(把线路垂直画出来就是T形),后者是在中间有一个回路(把线路垂直画出来,空出一条边就是
Π
\Pi
Π形)。
3.2. 等效条件
经过一系列解方程,可以得到两种网络互相等效的条件。
助记法:
Y形几条代三角一条边,所以阻值小。转化为三角形时是相加。
三角形相反,转化为Y形是合起来相除。
3.2.1. Y → Δ Y\to\Delta Y→Δ:星接转角接
下标对应阻值相加+下标对应阻值相乘除以对边阻值
{
R
12
=
R
1
+
R
2
+
R
1
R
2
R
3
R
23
=
R
2
+
R
3
+
R
2
R
3
R
1
R
31
=
R
3
+
R
1
+
R
3
R
1
R
2
\begin{cases} R_{12}=R_1+R_2+\frac{R_1R_2}{R_3}\\ R_{23}=R_2+R_3+\frac{R_2R_3}{R_1}\\ R_{31}=R_3+R_1+\frac{R_3R_1}{R_2} \end{cases}
⎩⎪⎨⎪⎧R12=R1+R2+R3R1R2R23=R2+R3+R1R2R3R31=R3+R1+R2R3R1
3.2.2. Δ → Y \Delta\to Y Δ→Y:角接转星接
下标存在的两个阻值相乘除以总阻值
{
R
1
=
R
12
R
31
R
12
+
R
23
+
R
31
R
2
=
R
23
R
12
R
12
+
R
23
+
R
31
R
3
=
R
31
R
23
R
12
+
R
23
+
R
31
\begin{cases} R_1=\frac{R_{12}R_{31}}{R_{12}+R_{23}+R_{31}}\\ R_2=\frac{R_{23}R_{12}}{R_{12}+R_{23}+R_{31}}\\ R_3=\frac{R_{31}R_{23}}{R_{12}+R_{23}+R_{31}} \end{cases}
⎩⎪⎨⎪⎧R1=R12+R23+R31R12R31R2=R12+R23+R31R23R12R3=R12+R23+R31R31R23
3.3. 应用:求解电桥电路( ∗ \ast ∗)
看到三个等值电阻为星接或角接直接考虑 Y − Δ Y-\Delta Y−Δ变换!!
对于不能平衡的电桥,我们可以考虑将其中部分已知的三端网络进行
Y
−
Δ
Y-\Delta
Y−Δ变换。随后化成可解的问题。
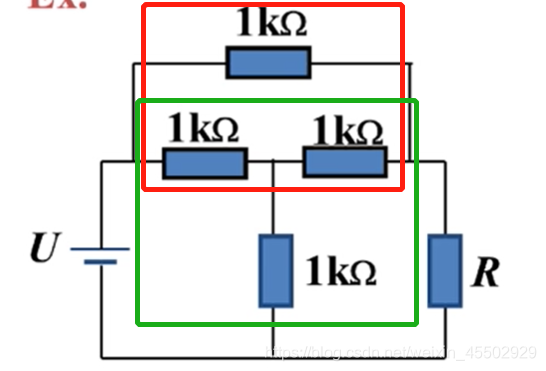
这个图中,1kΩ的四个电阻构成一个
Δ
\Delta
Δ形(红框)和Y形(绿框)网络。
分别对应将其化为星接和角接如下:
红框中三个电阻都为1/3kΩ。
星接转角接:
此为一个电阻
R
8
R_8
R8并联一个平衡电桥。
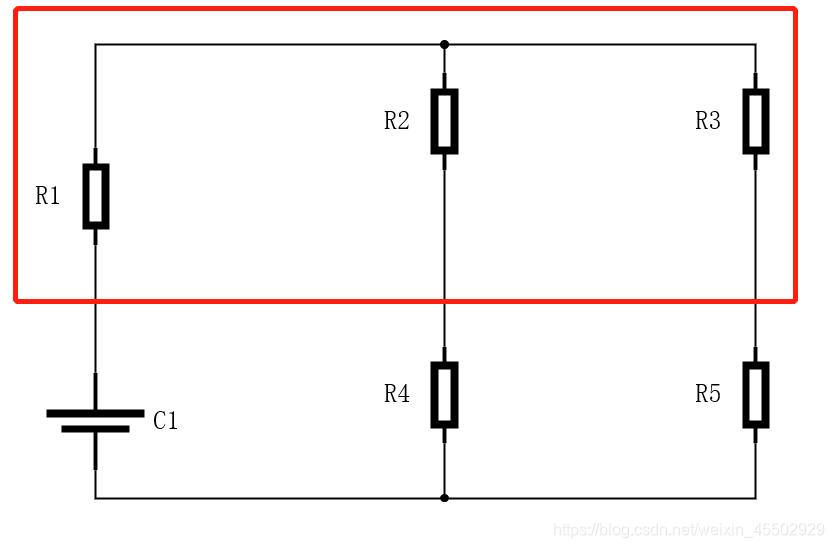
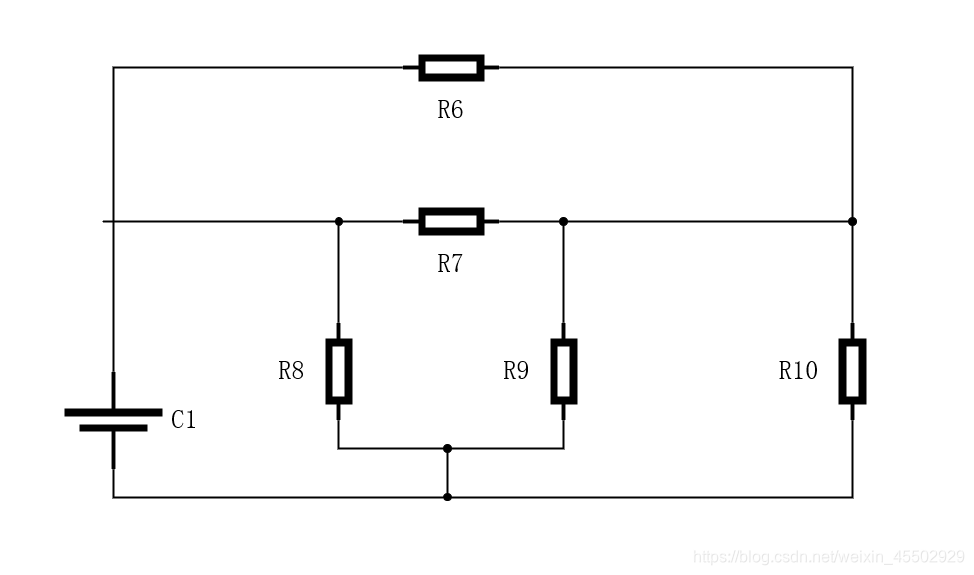
双T形网络
可以作为
Y
−
Δ
Y-\Delta
Y−Δ变换的综合应用。如果有两套共用节点的星接电路,且三支路电阻相同,则可以得知ab等势,可以将两网络的三个支路分别合并,成为一套网络,更易于求解。
复杂
Y
−
Δ
Y-\Delta
Y−Δ变换示例
4. 电源等效
4.1. 通解法,与带受控源的变换
使用“加压求流”和“加流求压”法。
这个方法的名字实际上是一句废话 就表明此方法的通解性。因为它体现了网络抽象+欧姆定律的综合使用的本质属性。相当于是定义法,即:
U
=
I
∗
□
I
=
U
/
□
U=I*\Box\\ I=U/\Box
U=I∗□I=U/□
这个思路也支持带有受控源的网络。
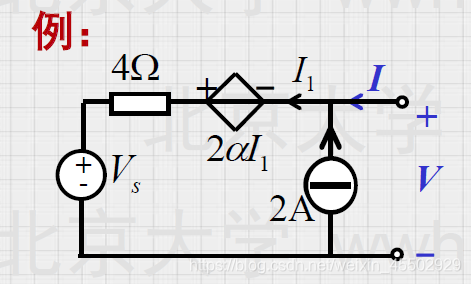
受控源要依靠一个控制量,这个量可能里受控源比较远,相当于两个端口分散在整个网络之中,为了保证这个元件的完整性,使用Thevenin-Norton转换时,时常只能适可而止,这可能会导致等效的简化结果不够简单,这时只能使用通解法。比如这个问题当中将,两个电压源串起来然后转化为Norton源,随后就丢失了
I
1
I_1
I1的信息,从这个角度上说等效是一种丢失信息的过程。
在这个题目中我们还可以看到当受控源的控制量和受控源在同一条支路当中时,这个受控源可以直接作为电阻的一部分!此题中可以看成 − 2 α -2\alpha −2α的一个电阻
4.2. 理想独立源的串并联
首先要说明一点,就是独立源具有和我们的理想电路模型有等效对应。
- 独立电流源相当于无限大电阻,或断路
- 独立电压源相当于导线,或短路。
它们二者所提供的电压、电流可以认为是这两种理想模型的附加属性。
也就是说,独立电流源是一个“电流确定的断路支路”,独立电压源是一个“电压确定的导线”
在分析外电路时,并在电压源两端网络无效,串在电流源支路的网络无效。
4.2.1. 独立源的串联
独立电压源串联
独立电压源 U S 1 , U S 2 ⋯ U S n U_{S1}, U_{S2}\cdots U_{Sn} US1,US2⋯USn串联,仍然相当于一条导线,其上短通性质并不改变,仍然为独立源。又由KVL可得其独立电压为 ∑ U S i \sum U_{Si} ∑USi。
独立电压源和独立电流源串联
串联支路中,一断则断。因而性质等同于断路,为一个独立电流源
因为电压源的外电流已经因为电流源而确定
所以相当于对外性质没有变化的独立电流源。
另外,独立电压源在这里就相当于一个虚拟电阻,可以分担提供一部分电压,所以原来的独立电流源上电压会减小。
这个电压也是独立电压源唯一的作用。
4.2.2. 独立源的并联
独立电流源的并联
多个断路并在一起仍然不能导通,所以仍然是独立电流源。由KCL得 I 1 , I 2 ⋯ I n I_1,I_2\cdots I_n I1,I2⋯In
独立电压源和独立电流源的串联
并联中只要一个支路为短路,一短则短。故为电压源,并入一个电流源后端口性质不变。同样地,电流源的目的是提供一部分电流,电压源的电流减小。
但是,在这里电流源并不能相当于一个支路,因为其方向和电压源所能提供的电流方向是相反的。
4.3. 实际独立源的等效变换
实际独立电压源和电流源
u
=
U
s
−
R
s
i
i
=
I
s
−
G
s
u
u=U_s-R_si\\ i=I_s-G_su
u=Us−Rsii=Is−Gsu
对比系数可得等效条件:
{
U
s
=
I
s
′
R
s
R
s
=
R
s
′
\begin{cases} U_s=I_s'R_s\\ R_s=R_s' \end{cases}
{Us=Is′RsRs=Rs′
含义:
- I s I_s Is为电流源电流, U s U_s Us为电压源电压, R s R_s Rs为待转化电源的内阻。
- 它们的“内阻”(对于电压源来说是串联,电流源是并联)相等。
关于这种源等效的可行性:
- 实际独立电压源:随电流增大而电压被分走。
- 实际独立电流源:随电压增大而电流被分走。
也就是说,两种源的电流电压均呈线性负相关,尽管内部的改变机理不同,仍然奇妙地实现了相同的结果。
判断含源网络是否等效( ∗ \ast ∗)
- 删掉无效元件:串入电阻(电压源)对电流源没有影响,并入电阻(电流源)对电压源没有影响。
- 串并联操作:电源串联先转化成实际电压源结构。电源并联先转化成实际电流源结构。受控源也可以进行类似独立源的操作。
- 退字诀:复杂的情况还是要回到最初的伏安特性上去。
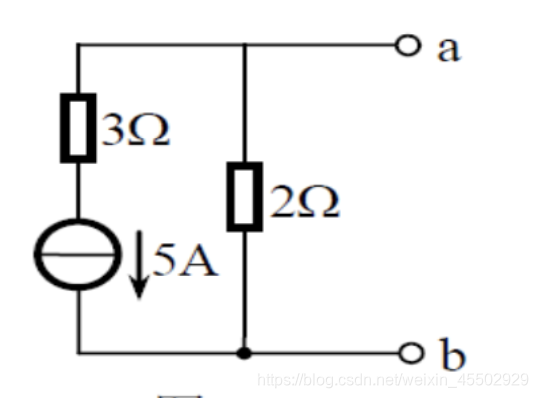
比如通过伏安特性我们就能验证,左边的支路就等效于一个电流源。
这和电流源串电压源的想法是一致的。因此我们最开始将串入的电压视作虚拟电阻是可行的。对总阻值没有影响,仅有的效果是分压。