Exercise solutions for 2nd edition

2nd Edition solutions

1. Introduction

1.1 What is an Algorithm?

Important points:

1. The non-ambiguity requirement for each step of an algorithm cannot be comprimised.
2. The range of inputs for which an algorithm works has to be specified carefully.
3. The same algorithm can be represented in several different ways.
4. There must exist several algorithms for solving the same problem.
5. Algorithms for the same problem can be based on very different ideas and can solve the problem with dramatically different speeds.

Greatest Common Divisor

Method 1:

Euclid's algorithm: for computing gcd(m, n)
Step 1: If n=0, return the value of m as the answer and stop; otherwise, proceed to Step2.
Step 2: Divide m by n and assign the value of the reminder to r.
Step 3: Assign the value of n to m and the value of r to n. Go to Step1.

ALGORITHM Euclid(m, n)
//Computes gcd(m, n) by Euclid's algorithm
//Input: Two nonnegative, not-both-zero integers m and n
//Output: Greatest common divisor of m and n
while n ≠ 0 do
  r ← m mod n 
  m ← n
  n ← r
return m

Proof of Euclid’s algorithm: for computing gcd(m, n)

Method 2:

Consecutive integer checking algorithm for computing gcd(m, n)
Step 1: Assign the value of min{m, n} to t.
Step 2: Divide m by t. If the remainder of this division is 0. go to Step3; otherwise, go to Step4.
Step 3: Divide n by t. If the remainder of this division is 0, return the value of t as the answer and stop; otherwise, proceed to Step4.
Step 4: Decrease the value of t by 1. Go to Step2.

This algorithm in the form presented, doesn’t work correctly when one of its input numbers is zero. It also underlines that it’s important to specify the set of an algorithm’s inputs explicitly and carefully.

Method 3:

Middle-school procedure for computing gcd(m, n)
Step 1: Find the prime factors of m.
Step 2: Find the prime factors of n.
Step 3: Identify all the common factors in the two prime expansions found in Step 1 and 2. (If p is a common factor occurring q1 and q2 times in m and n, respectively, it should be  repeated min{q1, q2} times.) 
Step 4: Compute the product of all the common factors and return it as the greatest common divisor of the numbers given.

Prime factors in Step 1 and 2 is not unambiguous. Also, Step 3 is not straightforward which makes Method 3 an unqualified algorithm. This is why Sieve of Eratosthenes needs to be introduced (generate consecutive primes not exceeding any given integer n > 1).

Sieve of Eratosthenes (Overview and Pseudocode part)

ALGORITHM Sieve(n)
//Implements the sieve of Eratosthenes
//Input: A positive integer n > 1
//Ouput: Array L of all prime numbers less than or equal to n
for p <- 2 to n do A[p] <- p
for p <-2 to floor(sqrt(n)) do
	if A[p] not equal to 0 //p hasn't been eliminated on previous passes
		j <- p * p
		while j <= n do
			A[j] <- 0  //mark elements as eliminated
			j <- j + p
//copy the remaining elements of A to array L of the primes
i <- 0
for p <- 2 to n do
	if A[p] not equal to 0	
		L[i] <- A[p]
		i <- i + 1
return L

Q: What is the largest number p whose multiples can still remain on the list to make further iterations of the algorithm necessary?

A: If p is a number whose multiples are being eliminated on the current pass, then the first multiple we should consider is $p^2$ because all its smaller multiples $2p,\dots ,(p-1)p$ have been eliminated on earlier passes through the list. Obviously, $p^2$ should not be greater than $n$.

Special care needs to be exercised if one or both input numbers are equal to 1: because mathematicians do not consider 1 to be a prime number, strictly speaking, the method does not work for such inputs.

1.2 Fundamentals of Algorithmic Problem Solving

• Understanding the Problem:

  Read the problem’s description carefully and ask questions if you have any doubts about the problem, do a few small examples by hand, think about special cases, and ask questions again if needed.

  An input to an algorithm specifies an instance of the problem the algorithm solves. If you fail to do this step, your algorithm may work correctly for a majority of inputs but crash on some “boundary” value. Remember a correct algorithm is not one that works most of the time, but one that works correctly for all legitimate inputs.

• Ascertaining the Capabilities of the Computational Device:

  RAM (random-access machine): instructions are executed one after another, one operation at a time, use sequential algorithms.

  New computers: execute operations concurrently, use parallel algorithms.

  Also, consider the speed and amount of memory the algorithm would take for different situations.

• Choosing between Exact and Approximate Problem Solving

• Algorithm Design Techniques

• Designing an Algorithm and Data Structures

• Methods of Specifying an Algorithm: natural language vs pseudocode

• Proving an Algorithm’s Correctness: the algorithm yields a required result for every legitimate input in a finite amount of time.

  A common technique for proving correctness is to use mathematical induction because an algorithm’s iterations provide a natural sequence of steps needed for such proofs.

  For an approximation algorithm, we usually would like to show that the error produced by the algorithm does not exceed a predefined limit.

• Analyzing an Algorithm: time and space efficiency, simplicity, generality.

  “A designer knows he has arrived at perfection not when there is no longer anything to add, but when there is no longer anything to take away.” —— Antoine de Saint-Exupery

• Coding an algorithm

  As a rule, a good algorithm is a result of repeated effort and rework.

1.3 Important Problem Types

The important problem types are sorting, searching, string processing, graph problems, combinatorial problems, geometric problems, and numerical problems.

• Sorting
  Rearrange the items of a given list in nondecreasing order according to a key.

  Although some algorithms are indeed better than others, there is no algorithm that would be the best solution in all situations.

  A sorting algorithm is called stable if it preserves the relative order of any two equal elements in its input, in-place if it does not require extra memory.

1.4 Fundamental Data Structures

Algorithms operate on data. This makes the issue of data structuring critical for efficient algorithmic problem solving. The most important elementary data structures are the array and the linked list. They are used for representing more abstract data structures such as the list, the stack, the queue/ priority queue (better implementation is based on an ingenious data structure called the heap), the graph (via its adjacency matrix or adjacency lists), the binary tree, and the set.

• Graph
  A graph with every pair of its vertices connected by an edge is called complete. A graph with relatively few possible edges missing is called dense; a graph with few edges relative to the number of its vertices is called sparse.

• Trees
  A tree is a connected acyclic graph. A graph that has no cycles but is not necessarily connected is called a forest: each of its connected components is a tree.

  The number of edges in a tree is always one less than the number of its vertices:|E| = |V| - 1. This property is necessary but not sufficient for a graph to be a tree. However, for connected graphs it is sufficient and hence provides a convenient way of checking whether a connected graph has a cycle.

  Ordered trees, ex. binary search trees. The efficiency of most important algorithms for binary search trees and their extensions depends on the tree’s height. Therefore, the following inequalities for the height h of a binary tree with n nodes are especially important for analysis of such algorithms: $$\lfloor {\log }_{2}n\rfloor \le h\le n-1$$

• Sets
  Representation of sets can be: a bit vector and list structure.

An abstract collection of objects with several operations that can be performed on them is called an abstract data type (ADT). The list, the stack, the queue, the priority queue, and the dictionary are important examples of abstract data types. Modern object-oriented languages support implementation of ADTs by means of classes.

2. Fundamentals of the Analysis of Algorithm Efficiency

Running time and memory space.

2.1 The Analysis Framework

The research experience has shown that for most problems, we can achieve much more spectacular progress in speed than in space.

• Measuring an Input’s Size
  When measuring input size for algorithms solving problems such as checking primality of a positive integer n. Here, the input is just one number, and it is this number’s magnitude that determines the input size. In such situations, it is preferable to measure size by the number b of bits in the n’s binary representation: $$b=\lfloor {\log }_{2}n\rfloor +1$$

• Units for Measuring Running Time
  The thing to do is to identify the most important operation of the algorithm, called the basic operation, the operation contributing the most to the total running time, and compute the number of times the basic operation is executed.

  Algorithms for mathematical problems typically involve some or all of the four arithmetical operations: addition, subtraction, multiplication and division. Of the four, the most time-consuming operation is division, followed by multiplication and then addition and subtraction, with the last two usually considered together.

  The established framework for the analysis of an algorithm’s time efficiency suggests measuring it by counting the number of times the algorithm’s basic operation is executed on inputs of size n.

• Orders of Growth
  logaⁿ = loga^b * logbⁿ

  Algorithms that require an exponential number of operations are practical for solving only problems of very small sizes.

• Worst-Case, Best-Case, and Average-Case Efficiencies
  If the best-case efficiency of an algorithm is unsatisfactory, we can immediately discard it without further analysis.

  The direct approach for investigating average-case efficiency involves dividing all instances of size n into several classes so that for each instance of the class the number of times the algorithm’s basic operation is executed is the same. Then a probability distribution of inputs is obtained or assumed so that the expected value of the basic operation’s count can be found.

  Amortized efficiency.

  Space efficiency is measured by counting the number of extra memory units consumed by the algorithm.

  The efficiencies of some algorithms may differ significantly for inputs of the same size. For such algorithms, we need to distinguish between the worst-case, average-case, and best-case efficiencies.

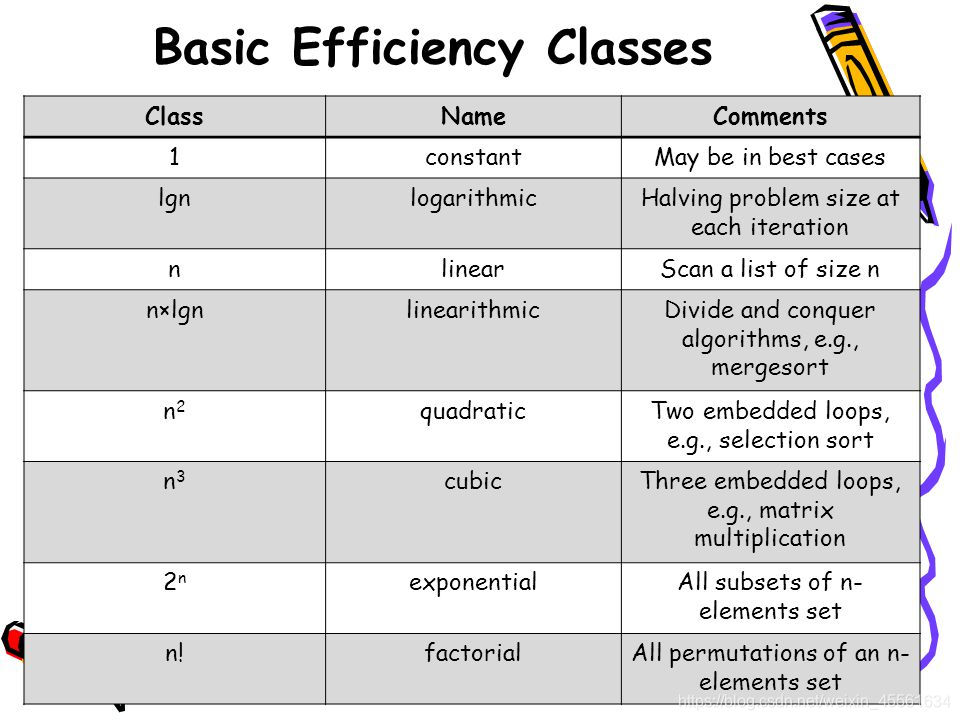
2.2 Asymptotic Notations and Basic Efficiency Classes

• O-notation
  O(g(n)) is the set of all functions with a lower or same order of growth as g(n) (to within a constant multiple, as n goes to infinity).

  Definition: A function t(n) is said to be in O(g(n)), denoted t(n) ∈ O(g(n)), if t(n) is bounded above by some constant multiple of g(n) for all large n, i.e., if there exist some positive constant c and some nonnegative integer n₀ such that t(n) ≤ cg(n) for all n ≥ n₀

• Ω-notation
  Ω(g(n)) is the set of all functions with a higher or same order of growth as g(n) (to within a constant multiple, as n goes to infinity).

  Definition: A function t(n) is said to be in Ω(g(n)), denoted t(n) ∈ Ω(g(n)), if t(n) is bounded below by some constant multiple of g(n) for all large n, i.e., if there exist some positive constant c and some nonnegative integer n₀ such that t(n) ≥ cg(n) for all n ≥ n₀

• Θ-notation
  Θ(g(n)) is the set of all functions with the same order of growth as g(n) (to within a constant multiple, as n goes to infinity).

  Definition: A function t(n) is said to be in Θ(g(n)), denoted t(n) ∈ Θ(g(n)), if t(n) is bounded both above and below by some constant multiples of g(n) for all large n, i.e., if there exist some positive constant c₁ and c₂ and some nonnegative integer n₀ such that c₂g(n) ≤ t(n) ≤ c₁g(n) for all n ≥ n₀.

• Useful Property Involving the Asymptotic Notations
  If t₁(n) ∈ O(g₁(n)) and t₂(n) ∈ O(g₂(n)), then t₁(n) + t₂(n) ∈ O(max{g₁(n), g₂(n)}) (also true for other two notations).
  
  L’Hôpital’s rule:
  
  Stirling’s Formula:
  

• Basic asymptotic efficiency classes
  

2.3 Mathematical Analysis of Nonrecursive Algorithms

1. Decide on parameter (or parameters) n indicating an input’s size.

2. Identify the algorithm’s basic operation. (As a rule, it is located in the inner most loop.)

3. Check whether the number of times the basic operation is executed depends only on the size of an input. If it also depends on some additional property, the worst-case, average-case, and, if necessary, best-case efficiencies have to be investigated separately.

4. Set up a sum expressing the number of times the algorithm’s basic operation is executed.

5. Using standard formulas and rules of sum manipulation, either find a closed-form formula for the count or, at the very least, establish its order of growth.

   Mathematical Analysis of Nonrecursive Algorithms

2.4 Mathematical Analysis of Recursive Algorithms

• Method of backward substitutions
• General Plan for Analyzing the Time Efficiency of Recursive Algorithms

1. Decide on a parameter (or parameters) indicating an input’s size.
2. Identify the algorithm’s basic operation.
3. Check whether the number of times the basic operation is executed can vary on different inputs of the same size; if it can, the worst-case, average-case, and best-case efficiencies must be investigated separately.
4. Set up a recurrence relation, with an appropriate initial condition, for the number of times the basic operation is executed.
5. Solve the recurrence or, at least, ascertain the order of growth of its solution.

• Tower of Hanoi

  To move n > 1 disks from peg 1 to peg 3 (with peg 2 as auxiliary), we first move recursively n − 1 disks from peg 1 to peg 2 (with peg 3 as auxiliary), then move the largest disk directly from peg 1 to peg 3, and, finally, move recursively n − 1 disks from peg 2 to peg 3 (using peg 1 as auxiliary). Of course, if n = 1, we simply move the single disk directly from the source peg to the destination peg.
  One should be careful with recursive algorithms because their succinctness may mask their inefficiency.

• BinRec(n): smoothness rule

ALGORITHM     BinRec(n)
//Input: A positive decimal integer n
//Output: The number of binary digits in n’s binary representation 
if n = 1 return 1
else return BinRec(floor(n/2)) + 1

2.6 Empirical Analysis of Algorithms

• General Plan for the Empirical Analysis of Algorithm Time Efficiency

1. Understand the experiment’s purpose.
2. Decide on the efficiency metric M to be measured and the measurement unit (an operation count vs. a time unit).
3. Decide on characteristics of the input sample (its range, size, and so on).
4. Prepare a program implementing the algorithm (or algorithms) for the experimentation.
5. Generate a sample of inputs.
6. Run the algorithm (or algorithms) on the sample’s inputs and record the data observed.
7. Analyze the data obtained.

• linear congruential method

ALGORITHM     Random(n, m, seed, a, b)
//Generates a sequence of n pseudorandom numbers according to the linear congruential method
//Input: A positive integer n and positive integer parameters m, seed, a, b 
//Output: A sequence r1,...,rn of n pseudorandom integers uniformly distributed among integer values between 0 and m − 1 //Note: Pseudorandom numbers between 0 and 1 can be obtained by treating the integers generated as digits after the decimal point

r0 ← seed
for i ← 1 to n do
	ri ← (a ∗ ri−1 + b) mod m

The simplicity of this pseudocode is misleading because the devil lies in the details of choosing the algorithm’s parameters. Here is a partial list of recommendations based on the results of a sophisticated mathematical analysis (see [KnuII, pp. 184–185] for details): seed may be chosen arbitrarily and is often set to the current date and time; m should be large and may be conveniently taken as 2^w, where w is the computer’s word size; a should be selected as an integer between 0.01m and 0.99m with no particular pattern in its digits but such that a mod 8 = 5; and the value of b can be chosen as 1.

3. Brute Force and Exhaustive Search

Brute force is a straightforward approach to solving a problem, usually directly based on the problem statement and definitions of the concepts involved.

3.1 Selection Sort and Bubble Sort

Selection Sort

We start selection sort by scanning the entire given list to find its smallest element and exchange it with the first element, putting the smallest element in its final position in the sorted list. Then we scan the list, starting with the second element, to find the smallest among the last $n-1$ elements and exchange it with the second element, putting the second smallest element in its final position. After $n-1$ passes, the list is sorted.

ALGORITHM SelectionSort(A[0..n − 1]) 
//Sorts a given array by selection sort
//Input: An array A[0..n − 1] of orderable elements 
//Output: Array A[0..n − 1] sorted in nondecreasing order 
for i ← 0 to n − 2 do
	min ← i
	for j ← i + 1 to n − 1 do
		if A[j] < A[min] 
			min ← j 
	swap A[i] and A[min]

The basic operation is the key comparison $A[j]<A[min]$. The number of times it is executed depends only on the array size $n$ and is given by the following sum:$$C(n)=\sum _{i=0}^{n-2}\sum _{j=i+1}^{n-1}1=\sum _{i=0}^{n-2}(n-1-i)=\frac{(n-1)n}{2}$$

Selection sort is a $\Theta (n^2)$ algorithm on all inputs. Note, however, that the number of key swaps is only $\Theta (n)$, or, more precisely, $n-1$ (one for each repetition of the $i$ loop). This property distinguishes selection sort positively from many other sorting algorithms.

Bubble Sort

Another brute-force application to the sorting problem is to compare adjacent elements of the list and exchange them if they are out of order. By doing it repeatedly, we end up “bubbling up” the largest element to the last position on the list. The next pass bubbles up the second largest element, and so on, until after $n-1$ passes the list is sorted.

ALGORITHM BubbleSort(A[0..n − 1])
//Sorts a given array by bubble sort
//Input: An array A[0..n − 1] of orderable elements
//Output: Array A[0..n − 1] sorted in nondecreasing order
for i ← 0 to n − 2 do
	for j ← 0 to n − 2 − i do
		if A[j + 1] < A[j] 
			swap A[j] and A[j + 1]

The number of key comparisons:
:$$C(n)=\sum _{i=0}^{n-2}\sum _{j=0}^{n-2-i}1=\sum _{i=0}^{n-2}(n-1-i)=\frac{(n-1)n}{2}\in \Theta (n^2)$$
The number of key swaps, however, depends on the input. In the worst case of decreasing arrays, it is the same as the number of key comparisons:
$$S_{worst}(n)=C(n)=1+\cdots +(n-1)=\frac{(n-1)n}{2}\in \Theta (n^2)$$
A little trick: if a pass through the list makes no exchanges, the list has been sorted and we can stop the algorithm.Though the new version runs faster on some inputs, it is still in $\Theta (n^2)$ in the worst and average cases.

Highlights:A first application of the brute-force approach often results in an algorithm that can be improved with a modest amount of effort.

3.2 Sequential search and Brute-Force String Matching

Sequential search

Trick1: if we append the search key to the end of the list, the search for the key will have to be successful, and therefore we can eliminate the end of list check altogether

ALGORITHM SequentialSearch2(A[0..n], K)
//Implements sequential search with a search key as a sentinel
//Input: An array A of n elements and a search key K
//Output: The index of the first element in A[0..n − 1] whose value is equal to K or −1 if no such element is found
A[n] ← K
i ← 0
while A[i] not equal to K do
	i ← i + 1 
	if i < n return i
else return −1

Trick2: if a given list is known to be sorted: searching in such a list can be stopped as soon as an element greater than or equal to the search key is encountered.

Brute-Force String Matching

ALGORITHM BruteForceStringMatch(T[0..n − 1], P[0..m − 1]) //Implements brute-force string matching
//Input: An array T[0..n − 1] of n characters representing a text and an array P[0..m − 1] of m characters representing a pattern 
//Output: The index of the first character in the text that starts a matching substring or −1 if the search is unsuccessful for i ← 0 to n − m do
	j ← 0
	while j < m and P[j] = T[i + j] do
		j ← j + 1 
	if j = m return i
return −1

The worst case is much worse: the algorithm may have to make all $m$ comparisons before shifting the pattern, and this can happen for each of the $n-m+1$ tries. Thus, in the worst case, the algorithm makes $m(n-m+1)$ character comparisons, which puts it in the $\mathrm{O}(nm)$ class.

For a typical word search in a natural language text, however, we should expect that most shifts would happen after very few comparisons (check the example again). Therefore, the average-case efficiency should be considerably better than the worst-case efficiency. Indeed it is: for searching in random texts, it has been shown to be linear, i.e., $\Theta (n)$.

3.3 Closest-Pair Problem and Convex-Hull Problem

Closest-Pair Problem

One of the important applications of the closest-pair problem is cluster analysis in statistics.

ALGORITHM BruteForceClosestPair(P)
//Finds distance between two closest points in the plane by brute force
//Input:AlistP of n(n ≥ 2)points p1(x1,y1),...,pn(xn,yn) //Output: The distance between the closest pair of points 
d ← ∞
for i ← 1 to n − 1 do
	for j ← i + 1 to n do
		d ← min(d, sqrt((xi − xj)^2 + (yi − yj)^2)) 
		//sqrt is square root
return d

Reason: even for most integers, square roots are irrational numbers that therefore can be found only approximately. Moreover, computing such approximations is not a trivial matter.

Solution: use square instead of square root.

The basic operation of the algorithm will be squaring a number. The number of times it will be executed can be computed as follows:
$$C(n)=\sum _{i=1}^{n-1}\sum _{j=i+1}^{n}2=2\sum _{i=1}^{n-1}(n-i)=n(n-1)\in \Theta (n^2)$$

Convex-Hull Problem

Applications:

• in computer an-imation, replacing objects by their convex hulls speeds up collision detection;
• used in computing accessibility maps produced from satellite images by Geographic Information Systems;
• used for detecting outliers by some statistical techniques;
• compute a diameter of a set of points, which is the largest distance between two of the points, needs the set’s convex hull to find the largest distance between two of its extreme points
• convex hulls are important for solving many optimization problems, because their extreme points provide a limited set of solution candidates

A line segment connecting two points $p_i$ and $p_j$ of a set of $n$ points is a part of the convex hull’s boundary if and only if all the other points of the set lie on the same side of the straight line through these two points (to check whether certain points lie on the same side of the line, we can simply check whether the expression $ax+by-c$ has the same sign for each of these points). Repeating this test for every pair of points yields a list of line segments that make up the convex hull’s boundary.

Time efficiency: $\mathrm{O}(n^3)$: for each of $\frac{n(n-1)}{2}$ pairs of distinct points, we may need to find the sign of $ax+by-c$ for each of the other $n-2$ points.

3.4 Exhaustive Search

Exhaustive search is simply a brute-force approach to combinatorial problems.

• Travelling Salesman Problem

  Find the shortest tour through a given set of $n$ cities that visits each city exactly once before returning to the city where it started.

  Weighted graph -> finding the shortest Hamiltonian circuit of the graph: a cycle that passes through all the vertices of the graph exactly once.

  Get all the tours by generating all the permutations of $n-1$ intermediate cities, compute the tour lengths, and find the shortest among them. The total number of permutations needed is $\frac{1}{2}(n-1)!$ if direction is implied.

• Knapsack Problem

  Given $n$ items of known weights $w$