C/C++语言：依次取出一个正整数的各位数字，及其变种形式

说明

本文主要介绍“依次取出一个整数的各位数字”及其变种形式

本来的面貌

PS：废话少说，先贴代码，后面再举两个例子；

#include<iostream>
#include<stack>
using namespace std;

将正整数n，从最低位向最高位，依次取出每位数，并将取出的每位数压栈
void function(int n){
	if(!n){//特殊情况特殊处理：当n=0时，直接输出，不执行后续代码
		cout << "位数：" << 1 << endl;
		cout << 0 << endl;
		return;
	}
	stack<int>stack;//栈
    int Count = 0;//统计该正整数，一共有几位数字
    while (n%10 || n/10){//循环条件：(n%10)与(n/10)不同时为0即可；循环结束条件：(n%10)与(n/10)同时为0即结束循环
        int Digit = n % 10;//取出正整数的最低位数字
        n = n/10;//取出最低位数字后，剩余的
        Count++;//个数加1
        stack.push(Digit);//将取出的最低位数字，压栈
    }//注意：循环结束后，n=0
    
    输出
    cout << "位数：" << Count << endl;//
    cout << "位数：" << stack.size() << endl;//两种方式均可统计一共有几位数字
    while(!stack.empty()){//出栈
        int temp = stack.top();//取栈顶元素
        stack.pop();//出栈，但是并不返回栈顶元素
        cout << temp << " ";//显示结果为：依次从最高位到最低位输出每位数字
    }
}

测试函数

int main(){
	function(123);
	return 0;
}

结果
在这里插入图片描述
///
下面是我的分析过程：
例子一：依次取出 3546 的各个数字
3546 % 10 = 6 //取出最低位
3546 / 10 = 354

354 % 10 = 4 //取出
354 / 10 = 35

35 % 10 = 5 //取出
35 / 10 = 3

3 % 10 = 3 //取出
3 / 10 = 0 //注：不同时为0，还要继续循环

0 % 10 = 0 //没进循环，不取
0 / 10 = 0 //注：同时为0，循环结束

例子二：依次取出 306 的各位数字
306 % 10 = 6 //取出
306 / 10 = 30

30 % 10 = 0 // 取出
30 / 10 = 3

3 % 10 = 3 //取出
3 / 10 = 0 //注：不同时为0，还要继续循环

0 % 10 = 0 //没进循环，不取
0 / 10 = 0 //注：同时为0，循环结束

PS：最后，方法有很多中，随便都能百度到，从大一到大四，前前后后也写过很多中版本，感觉这个还算比较简便吧，写在这里，记录一下，方便查看哈哈。第一次写博客，感觉好啰嗦哦！

-----------------------------------------------------------------------------------------------------------------------2022-3-31更新----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

变种一：计算一个正整数的各位数字之和

//计算一个正整数的各位数字之和
int function(int n){
    int count = 0;//正整数n的位数
    int sum = 0;
    while(n%10 || n/10){
        int digit = n % 10;//取最低位
        n = n/10;//更新
        count++;
        //
        sum = sum + digit;
    }
    return sum;
}

变种二：判断水仙花数

//编写判断水仙花数的函数；
//PS:水仙花数是指一个 3 位数，它的每个位上的数字的 3次幂之和等于它本身。
// 例如：因为1^3 + 5^3+ 3^3 = 153，所以153是水仙花数
bool function(int n){
    int temp = n;//暂存，非常容易错
    int count = 0;//
    int sum = 0;
    while(n%10 || n/10){
        int digit = n%10;//取最低位
        n = n/10;
        count++;
        //
        sum = sum + digit*digit*digit;
    }//循环结束，n=0

    if(sum == temp)
        return true;
    else
        return false;
}

变种三：判断是否是对称数

对称数定义：一个整数，正序和倒序都对称的数，如11、22、12321、123321等都是对称数，而123不是对称数；

处理方式一

分析

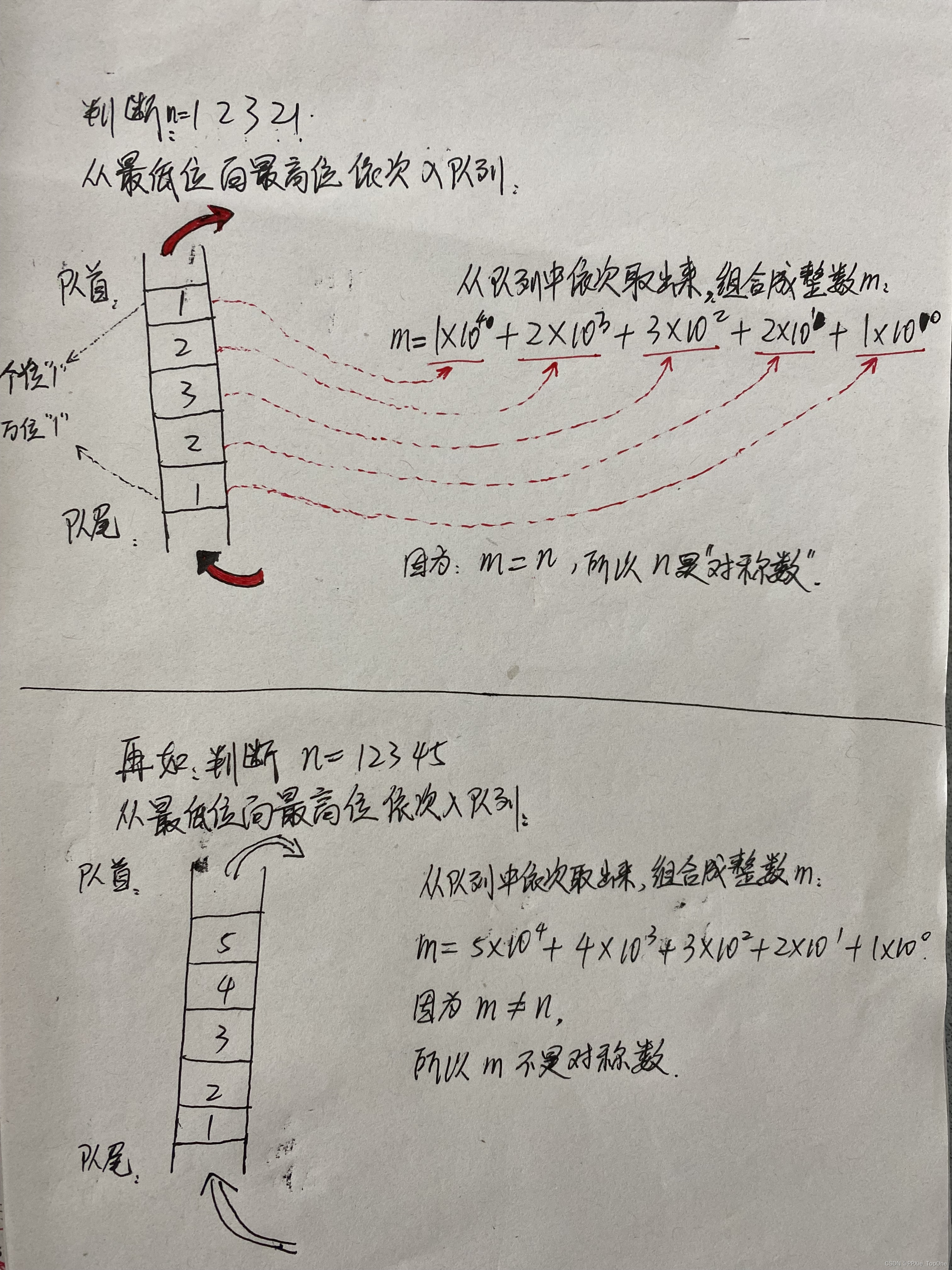
先从最低位向最高位取出整数n的每一位数，存放在队列中；
然后出队列重新组合成一个新的整数m，最后与整数n进行比较，若m==n则说明是对称数，如下图：

代码

//homework.h文件
#include<iostream>
#include<queue>
using namespace std;

bool function(int n){
    int count = 0;//
    queue<int>Queue;
    int temp = n;//暂存
    while(n%10 || n/10){
        int digit = n%10;
        n = n/10;
        count++;
        //
        Queue.push(digit);//入队
    }//结束n=0
  
    int sum = 0;
    int i = count-1;
    while(!Queue.empty()){
        sum = sum + Queue.front()*pow(10,i);//返回队首元素
        Queue.pop();//只删不返回
        i--;
    }
    //
    if(sum == temp)
        return true;
    else
        return false;
}

处理方式二

分析

先从最低位向最高位取出整数n的每一位数，放在数组中；
然后再统计 i、j 指向元素相等的个数是否等于原整数位数的一半：用两个指针 i、j 分别指向数组第一个和最后一个元素位置，若i、j 指向的元素相等则 i++、j–

代码


bool function(int n){
    int temp = n;//暂存
    int test[10];//正整数n最多不超过10位
    int count = 0;
    while(n%10 || n/10){
        int digit = n%10;//取出最低位
        n = n/10;//更新
        count++;
        //
        test[count-1] = digit;
    }//执行后n=0
   
    int i = 0,j = count-1;//指针
    int m = 0;
    while(test[i] == test[j] && i<j){
        i++;
        j--;
        m++;
    }
    if(m == count/2)
        return true;
    else
        return false;
}