深度优先搜索(Depth First Search,DFS)
PS:图的深度优先搜索DFS,代码实现有多种,这里:
1、图的存储:邻接矩阵
2、辅助工具: 栈stack,栈中装的是 顶点对象
访问标志数组visited,int 型
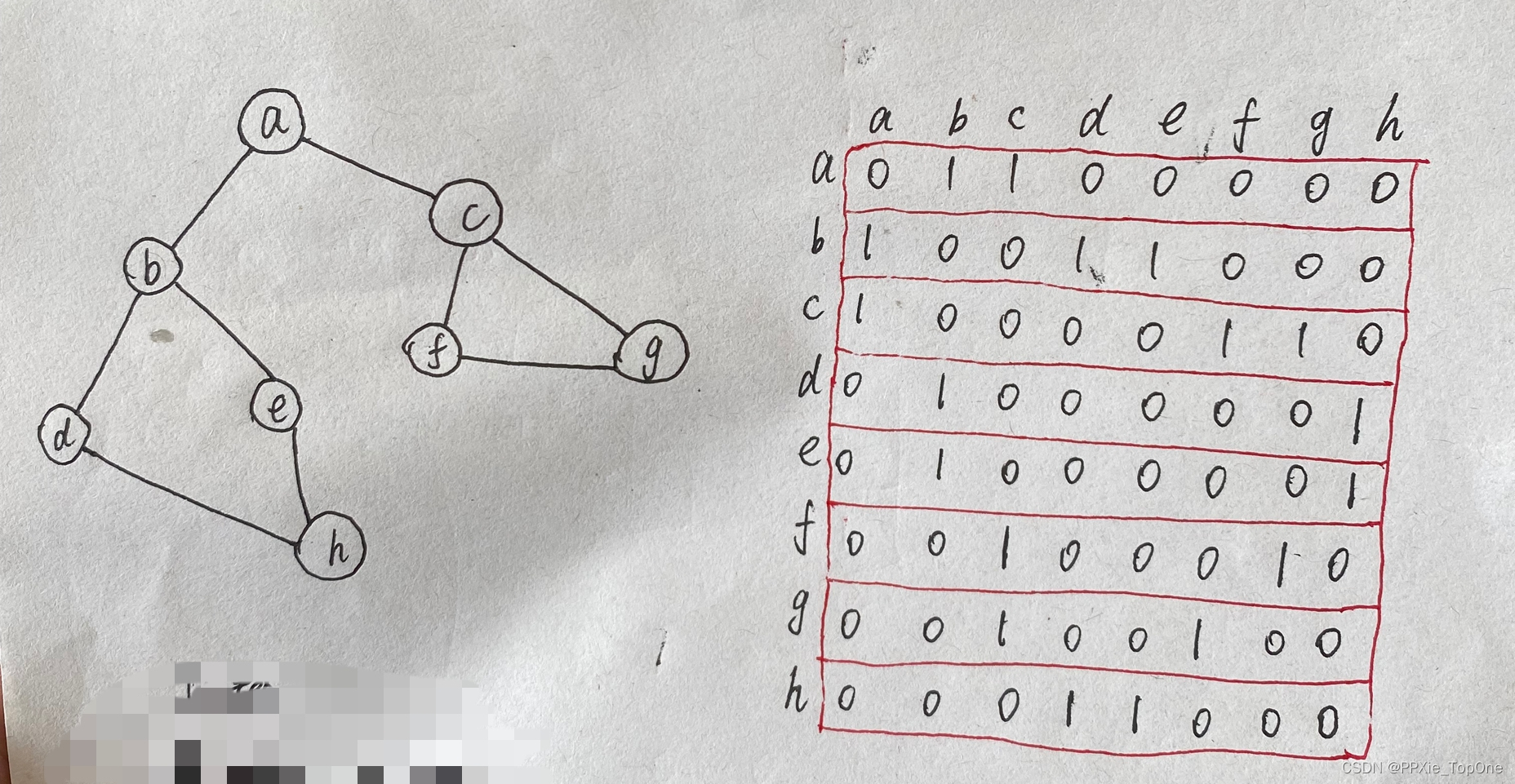
一、图
无向图G 及其邻接矩阵表示
二、实现
1、从 a 开始访问,DFS 顺序该为:a b d h e c f g
2、思路:
- 说明:1)每个顶点都是先访问之后,再入栈 ;
2)栈为空时搜索结束! - 第一步:假如某一时刻栈顶元素是 v:查看与栈顶元素 v 是否有相邻的且还没有被访问过的顶点 w。
- 第二步:若有,先访问w后,再将顶点w入栈。则新的栈顶元素为 w,再重复第一步(判断与新的栈顶元素 w是否有相邻的且还没有被访问过的顶点)
- 第三步:若没有,将栈顶元素 v 出栈。如果栈顶元素 v 出栈后,栈非空且新的栈顶元素为s,再重复第一步(判断与新的栈顶元素 s是否有相邻的且还没有被访问过的顶点);如果栈顶元素 v出栈后,栈为空,则搜索结束!
3、(傻瓜式)分析
1)先访问a,再将a压栈,栈顶元素为a;
2)查看与栈顶元素a是否有相邻的且还有没访问过的顶点,有顶点b,访问顶点b并压栈,新的栈顶元素为b;
3)查看与栈顶元素b是否有相邻的且还有没访问过的顶点,有顶点d,访问顶点d并压栈,新的栈顶元素为d;
4)查看与栈顶元素d是否有相邻的且还有没访问过的顶点,有顶点h,访问顶点h并压栈,新的栈顶元素为h;
5) 查看与栈顶元素h是否有相邻的且还有没访问过的顶点,有顶点e,访问顶点e并压栈,新的栈顶元素为e;
6) 查看与栈顶元素e是否有相邻的且还有没访问过的顶点,没有。将栈顶元素e出栈(回溯),栈非空且新的栈顶元素为h;
7)查看与栈顶元素h是否有相邻的且还有没访问过的顶点,没有。将栈顶元素h出栈(回溯),栈非空且新的栈顶元素为d;
8)查看与栈顶元素d是否有相邻的且还有没访问过的顶点,没有。将栈顶元素d出栈(回溯),栈非空且新的栈顶元素为b;
9)查看与栈顶元素b是否有相邻的且还有没访问过的顶点,没有。将栈顶元素b出栈(回溯),栈非空且新的栈顶元素为a;
10)查看与栈顶元素a是否有相邻的且还有没访问过的顶点,有顶点c,访问顶点c并压栈,新的栈顶元素为c;
11)查看与栈顶元素c是否有相邻的且还有没访问过的顶点,有顶点f,访问顶点f并压栈,新的栈顶元素为f;
12)查看与栈顶元素f是否有相邻的且还有没访问过的顶点,有顶点g,访问顶点g并压栈,新的栈顶元素为g;
13)查看与栈顶元素g是否有相邻的且还有没访问过的顶点,没有。将栈顶元素g出栈(回溯),栈非空且新的栈顶元素为f;
14)查看与栈顶元素f是否有相邻的且还有没访问过的顶点,没有。将栈顶元素f出栈(回溯),栈非空且新的栈顶元素为c;
15)查看与栈顶元素c是否有相邻的且还有没访问过的顶点,没有。将栈顶元素c出栈(回溯),栈非空且新的栈顶元素为a;
16)查看与栈顶元素a是否有相邻的且还有没访问过的顶点,没有。将栈顶元素a出栈(回溯),栈为空,则搜索结束;
4、代码
头文件:home10.h
#include<iostream>
#include "stack"
using namespace std;
#define MVNum 100 //图的顶点个数,最大值Max_Vertex_Num
typedef char VertexType; //顶点类型,char
typedef int ArcType; //权值类型,int
int visited[MVNum]={0}; //访问标志数组,初值全为0,表示所有顶点都没有被访问过
stack<VertexType>Stack;//栈
typedef struct {
VertexType vertexs[MVNum]; //顶点数组,从0开始存
ArcType arcs[MVNum][MVNum]; //邻接矩阵,从arcs[0][0]开始存
int vernum,arcnum; //图当前的顶点个数、边个数
}AMGraph;//图的邻接矩阵
/*
* TODO:查找与顶点v相邻的且是没有被访问过的顶点w
* 若有就返回w,没有就返回NULL
* */
VertexType haveAdjacency(AMGraph G, VertexType v){
//找出v顶点对应的数组下标i
int i = 0;
while (v != G.vertexs[i]) {
i++;
}
//扫描邻接矩阵G.arcs中下标为i的一维数组,查找与顶点v相邻的且是没有被访问过的顶点w
int j = 0;
while((G.arcs[i][j] != 1 || visited[j] != 0) && j < G.vernum){
//循环结束条件:(G.arcs[i][j] == 1 && visited[j] == 0)即找到与v相邻的,结束 或者 根本就没有与v相邻的,也结束
j++;
}
if(j < G.vernum){//有这样一个顶点w,返回w
VertexType w = G.vertexs[j];
return w;
}
else if(j >= G.vernum)//没有,返回NULL
return NULL;
}
/*
* TODO:顶点v访问过之后,相应地在visited数组中把它置1
* */
void setVisited(AMGraph G, VertexType v){
int i = 0;
while (v != G.vertexs[i]) {//查找顶点v对应的数组下标
i++;
}
visited[i] = 1;
}
/*
* TODO:
* 注意:顶点都是先被访问,然后再入栈;
* v是栈顶元素,每次都是判断与栈顶元素v是否有相邻的且是没有被访问过的顶点w:
* 有,那么就访问顶点w并入栈,然后再递归判断与新的栈顶元素w是否有相邻的且未被访问过的顶点,
* 没有,那么栈顶元素出栈,然后再递归判断与新的栈顶元素r是否有相邻的且未被访问过的顶点.
* */
void DFS(AMGraph G, VertexType v){
//查看是否有,与栈顶v相邻的且还没有被访问过的顶点w,有就返回顶点w,没有就返回NULL
VertexType w = haveAdjacency(G,v);
if(w){//有
cout << w << " ";//访问
setVisited(G,w);//w访问之后,相应地在visited数组中把它置1
Stack.push(w);
//递归
DFS(G,w);
// return;
}
else{//没有,这个时候栈一定是非空的
Stack.pop();//pop:仅删除栈顶元素,但不返回
//
if(Stack.empty())//取出栈顶后,栈空,搜索结束
return;
else{//取出栈顶后,栈非空,继续判断
VertexType w = Stack.top();//top:仅返回栈顶元素,但不删除
DFS(G,w);
// return;
}
}
}
/*
* TODO:从图中的顶点v开始深度优先搜索
* */
void Function(AMGraph G, VertexType v){
cout << v << " ";//访问
setVisited(G,v);//访问之后,给visited数组置1
Stack.push(v);
DFS(G,v);
}
测试函数:home10_main.cpp
//
// Created by dong on 2022-03-16.
//
#include "home10.h"
int main(){
AMGraph G;
G.vernum = 8;//8个顶点
G.arcnum = 9;
//
char test[8]={'a','b','c','d','e','f','g','h'};
for(int i = 0; i < 8; i++)
G.vertexs[i] = test[i];
//
int a[8][8]={0,1,1,0,0,0,0,0,
1,0,0,1,1,0,0,0,
1,0,0,0,0,1,1,0,
0,1,0,0,0,0,0,1,
0,1,0,0,0,0,0,1,
0,0,1,0,0,0,1,0,
0,0,1,0,0,1,0,0,
0,0,0,1,1,0,0,0};
for(int i = 0; i < 8; i++)
for(int j = 0; j < 8; j++)
G.arcs[i][j] = a[i][j];
//
Function(G,'a');
return 0;
}
结果
5、最后
当然了,这个代码还有很多可以优化的,比如栈中存顶点的下标而不是整个顶点,可以去试试!