09动态规划——投资问题

09基于动态规划的投资问题

简述动态规划

动态规划：

动态规划(Dynamic Programming)是运筹学的一个分支，是一种使用多阶段决策过程的最优的通用方法。它不是某种具体的算法，而是算法设计技术，对求出目标函数在一定约束条件下的极值这样的问题，DP提供了高效的解决思路。

用DP解决的问题通常具有以下两个特征：

1.问题由交叠的子问题构成，将子问题记录在表中，可避免重复计算。
2.问题满足最优化法则。

举个有关DP的简单例子：

初学程序设计的时候，可能多数人都遇到过“爬楼梯问题”。给定几种合规的走法（如只允许1格1爬、2格1爬和3格1爬），爬n格（如30格）楼梯共有几种爬法。

不少人的第一选择是递归法：

int fun(int n){
	if(n==1) return 1;//1
	else if(n==2) return 2;//1+1、2
	else if(n==3) return 4;//1+1+1、1+2、2+1、3
	return fun(n-1)+fun(n-2)+fun(n-3);
}

但是，递归法的效率显然不高，存在大量的重复计算。比如计算fun(5)和fun(6)时，都重复计算了fun(4)的结果，当然，递归算法整个程序执行过程，造成的冗余重复更多。

有什么办法可以减少重复计算，最好使每一个fun(k) (k∈[1,n]) 至多计算一次？

采用动态规划的思想！将每次计算得到的值保存起来，供后面的计算直接调用，这就大幅度提高了运算效率。

#define N 31
int funDP(int n){
	int a[N];
	a[1]=1;a[2]=2;a[3]=4;
	for(int i=4;i<=n;i++){
		a[i]=a[i-1]+a[i-2]+a[i-3];
	}
	return a[n];
}

易得，funDP()=O(n). 动态规划的妙处值得用心去体会。

1.问题

本文主要讨论基于DP的投资问题。

问题的一般性描述：

设有 m 元钱，n 项投资，函数 f_i(x) 表示将 x 元投入第 i 项项目所产生的效益，i=1,2,…,n.
问：如何分配这 m 元钱，使得投资的总效益最高？

组合优化问题，假设分配给第 i 个项目的钱数是 x_i，问题描述为：

目标函数：max { f₁(x₁) + f₂(x₂)+ … + f_n(x_n)},
约束条件：x₁ + x₂ + … + x_n = m , x_i ∈ N.

2.解析

设 f_k(x) = d 表示：x 万元投给第 k 个项目的效益为 d.
设 A_i(x) = a 表示：新加第i个项目，共分配 x 万元时，第i项分配了a元；
设 F_k(x) = s 表示：x 万元投给前 k 个项目最大效益为 s.

递推方程：F_k(x) = max{ f_k ( A_k ) + F_k-1(x - A_k) }, k = 1,2,…,n.
边界条件：F₁(x) = f₁(x), F_k(0) = 0, k = 1,2,…,n.

举个栗子

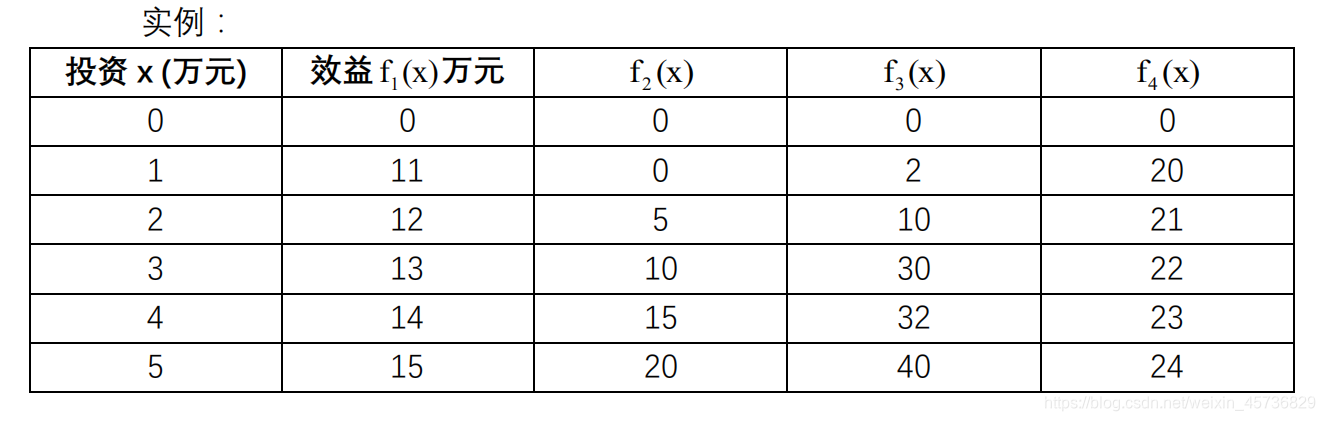
假设各项目投资金额与生产效益之间的关系如下表：
在这里插入图片描述
总投资金额 m=5 万元, 项目数 n=4 , 单项目分配额 x ∈ [0,5], 如何在约束条件下，得到投资利益最大化？

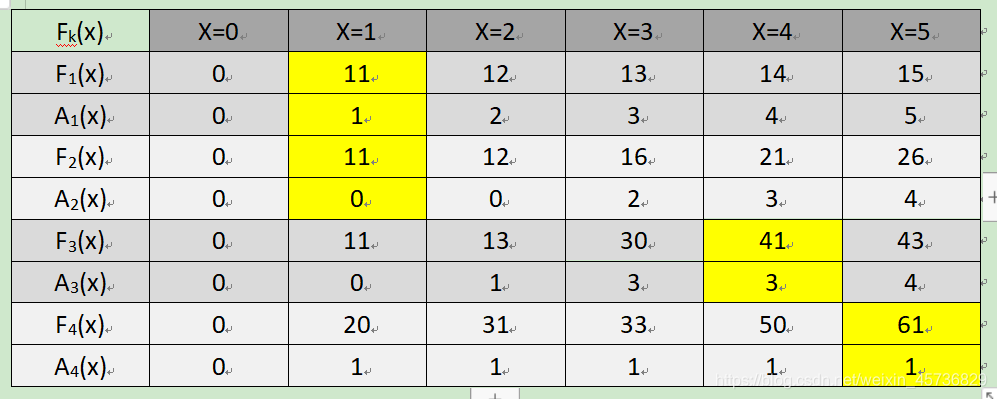
根据实例逐一推导：

k=1, x ∈ [0,5], 求 F₁(x)，即求x万元投给前1个项目的最大效益
x = 0：F₁(0) = 0;
x = 1(前1个项目共分配1元)：F₁(1) = f₁(1) = 11;
x = 2：F₁(2) = f₁(2) = 12;
x = 3：F₁(3) = f₁(3) = 13;
x = 4：F₁(4) = f₁(4) = 14;
x = 5：F₁(5) = f₁(5) = 15.
k=2, x ∈ [0,5], 求 F₂(x)，即求x万元投给前2个项目的最大效益
x = 0：F₂(0) = f₂(0) + F₁(0) = 0.
x = 1(前2个项目共分配1元)：
A₂(1)=1(前2项共分配1万元时给第 2 项分配1 元), F₂(1) = f₂(1)+F₁(0) = 0;
A₂(1)=0(前2项共分配1万元时给第 2 项分配0 元), F₂(1) = f₂(0)+F₁(1) = 11.
比较得 F₂(1)<–max{ F₂(1) } = 11.
x = 2：
A₂(2)=2, F₂(2) = f₂(2)+F₁(0) = 5;
A₂(2)=1, F₂(2) = f₂(1)+F₁(1) = 11;
A₂(2)=0, F₂(2) = f₂(0)+F₁(2) = 12.
比较得 F₂(2)<–max{ F₂(2) } = 12.
x = 3：
A₂(3)=3, F₂(3) = f₂(3)+F₁(0) = 10;
A₂(3)=2, F₂(3) = f₂(2)+F₁(1) = 16;
A₂(3)=1, F₂(3) = f₂(1)+F₁(2) = 12;
A₂(3)=0, F₂(3) = f₂(0)+F₁(3) = 13.
比较得 F₂(3)<–max{ F₂(3) } = 16.
x = 4：
A₂(4)=4, F₂(4) = f₂(4)+F₁(0) = 15;
A₂(4)=3, F₂(4) = f₂(3)+F₁(1) = 21;
A₂(4)=2, F₂(4) = f₂(2)+F₁(2) = 17;
A₂(4)=1, F₂(4) = f₂(1)+F₁(3) = 13;
A₂(4)=0, F₂(4) = f₂(0)+F₁(4) = 14.
比较得 F₂(4)<–max{ F₂(4) } = 21.
x = 5：
A₂(5)=5, F₂(5) = f₂(5)+F₁(0) = 20;
A₂(5)=4, F₂(5) = f₂(4)+F₁(1) = 26;
A₂(5)=3, F₂(5) = f₂(3)+F₁(2) = 22;
A₂(5)=2, F₂(5) = f₂(2)+F₁(3) = 18;
A₂(5)=1, F₂(5) = f₂(1)+F₁(4) = 14;
A₂(5)=0, F₂(5) = f₂(0)+F₁(5) = 15.
比较得 F₂(5)<–max{ F₂(5) } = 26.
k=3, x ∈ [0,5], 求 F₃(x)，即求x万元投给前3个项目的最大效益
x = 0：F₃(0) = f₃(0) + F₂(0) = 0.
x = 1(前3个项目共分配1元)：
A₃(1)=1(前3项共分配1万元时给第 3 项分配1 元), F₃(1) = f₃(1)+F₂(0) = 2;
A₃(1)=0(前3项共分配1万元时给第 3 项分配0 元), F₃(1) = f₃(0)+F₂(1) = 11.
比较得 F₃(1)<–max{ F₃(1) } = 11.
x = 2：
A₃(2)=2, F₃(2) = f₃(2)+F₂(0) = 10;
A₃(2)=1, F₃(2) = f₃(1)+F₂(1) = 13;
A₃(2)=0, F₃(2) = f₃(0)+F₂(2) = 12.
比较得 F₃(2)<–max{ F₃(2) } = 13.
x = 3：
A₃(3)=3, F₃(3) = f₃(3)+F₂(0) = 30;
A₃(3)=2, F₃(3) = f₃(2)+F₂(1) = 21;
A₃(3)=1, F₃(3) = f₃(1)+F₂(2) = 14;
A₃(3)=0, F₃(3) = f₃(0)+F₂(3) = 16.
比较得 F₃(3)<–max{ F₃(3) } = 30.
x = 4：
A₃(4)=4, F₃(4) = f₃(4)+F₂(0) = 32;
A₃(4)=3, F₃(4) = f₃(3)+F₂(1) = 41;
A₃(4)=2, F₃(4) = f₃(2)+F₂(2) = 22;
A₃(4)=1, F₃(4) = f₃(1)+F₂(3) = 18;
A₃(4)=0, F₃(4) = f₃(0)+F₂(4) = 21.
比较得 F₃(4)<–max{ F₃(4) } = 41.
x = 5：
A₃(5)=5, F₃(5) = f₃(5)+F₂(0) = 40;
A₃(5)=4, F₃(5) = f₃(4)+F₂(1) = 43;
A₃(5)=3, F₃(5) = f₃(3)+F₂(2) = 42;
A₃(5)=2, F₃(5) = f₃(2)+F₂(3) = 26;
A₃(5)=1, F₃(5) = f₃(1)+F₂(4) = 23;
A₃(5)=0, F₃(5) = f₃(0)+F₂(5) = 26.
比较得 F₃(5)<–max{ F₃(5) } = 43.
k=4, x ∈ [0,5], 求 F₄(x)，即求x万元投给前4个项目的最大效益
由于项目总数为4，此时可以只算x=5的情况，直接得出此问题的最大收益情况。
x = 5：
A₄(5)=5, F₄(5) = f₄(5)+F₃(0) = 24;
A₄(5)=4, F₄(5) = f₄(4)+F₃(1) = 34;
A₄(5)=3, F₄(5) = f₄(3)+F₃(2) = 35;
A₄(5)=2, F₄(5) = f₄(2)+F₃(3) = 51;
A₄(5)=1, F₄(5) = f₄(1)+F₃(4) = 61;
A₄(5)=0, F₄(5) = f₄(0)+F₃(5) = 43.
比较得 F₄(5) <-- max{ F₄(5) } = 61.

在这里插入图片描述
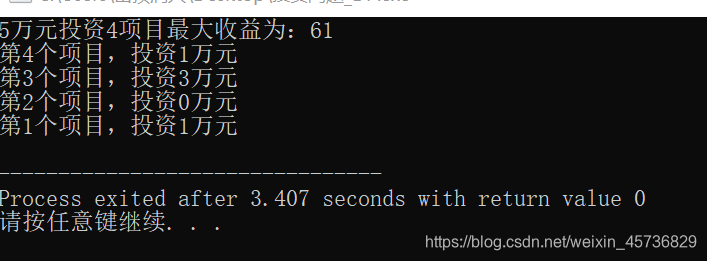
由此可知，F₄(5) = 61：此结果为最大收益。5万元分配4个项目最大收益61万元。
A₁(1)=1：共 1 万，1 万分配给第 1 个项目，剩余 5-1=4 万；
A₂(1)=0：共 1 万，0 万分配给第 2 个项目，剩余 4-0=4 万；
A₃(4)=3：共 4 万，3 万分配给第 3 个项目，剩余 4-3=1 万；
A₄(5)=1：共 5 万，1 万分配给第 4 个项目，剩余 1-1=0 万。

3.设计

#define N 5//项目数
#define M 6//投资总额
//aItem[3][2]表示共投资2万元第3个项目的投资金额，用于追溯路径
double aItem[N][M] = {0};
//Fsum[3][2]表示前3个项目共投资2万元的最大收益
double Fsum[N][M] = {0};

double investMax(double f[N][M]) {		
	//前1个项目的情况，即边界
	for i ← 0 to M-1
		do 
		Fsum[1][i] ← f[1][i];
		aItem[1][i] ← i;
	end for
	
	//第k个项目
	for k ← 2 to N-1
		//k个项目共分配m万元
		for m ← 1 to M-1
			max ← -1,temp ← 0;
			//第k个项目分配a万元
			for a ← 0 to m	
				if (f[k][a] + Fsum[k-1][m - a] > max) then
					do 
					max ← f[k][a] + Fsum[k-1][m - a];
					temp ←  a;
				end if		
			end for a
			
			Fsum[k][m] ← max;
			aItem[k][m] ← temp;
			
		end for m
	end for k
	
	return Fsum[N-1][M-1];
}

4.分析

算法复杂度为：n*((m+1+2)*m/2)=n*m*(m+3)/2.
investMax(n,m)=O(nm²).

5.源码

#include<iostream>
#define N 5//项目数
#define M 6//投资总额

using namespace std;

//aItem[3][2]表示共投资2万元第3个项目的投资金额，用于追溯路径
double aItem[N][M] = {0};
//Fsum[3][2]表示前3个项目共投资2万元的最大收益
double Fsum[N][M] = { 0 };

double investMax(double f[N][M]) {
		
	//前1个项目的情况，即边界
	for (int i = 0; i <= M-1; i++) {
		Fsum[1][i] = f[1][i];
		aItem[1][i] = i;
	}
	//第k个项目
	for (int k = 2; k <= N-1; k++) {
		//k个项目共分配m万元
		for (int m = 1; m <= M-1; m++) {
			double max = -1,temp=0;
			//第k个项目分配a万元
			for (int a = 0; a <= m; a++) {
				if (f[k][a] + Fsum[k-1][m - a] > max) {
					max = f[k][a] + Fsum[k-1][m - a];
					temp =  a;
				}
			}
			Fsum[k][m] = max;
			aItem[k][m] = temp;
		}
	}

	return Fsum[N-1][M-1];
}

void printInfo() {
	int index = M - 1;
	for (int i = N - 1; i > 0; i--) {
		cout << "第" << i << "个项目，投资" << aItem[i][index] << "万元" << endl;
		index -= aItem[i][index];
	}
}

int main() {

	double f[N][M] = {//f[1][2]表示投第1个项目2万元所产生的效益
		{0, 0, 0, 0, 0, 0},//没有第0个项目
		{0,11,12,13,14,15},
		{0, 0, 5,10,15,20},
		{0, 2,10,30,32,40},
		{0,20,21,22,23,24}
	};
	cout << M-1 <<"万元投资"<<N-1<<"项目最大收益为：" << investMax(f) << endl;
	printInfo();
	return 0;
}

点击前往Github查看源码