利用NetworkX库,在预先构建好的路网图中,我们可以精确地计算出从指定起点到终点的最短路径。这一过程涉及在图结构内智能地搜索,以找到从起始节点到目标节点之间成本(如距离、时间等)最低的路径。随后,为了增强路径的可视化效果和理解度,我们使用图形化工具matplotlib结合OSMnx的绘图功能来展示整个路网图,并特别高亮显示计算出的最短路径。这样,道路、交叉点以及最关键的路径走向都被清晰地呈现出来,能够直观地把握路径的详细信息以及整个路网的布局结构。
第一步先根据下载路网数据,并对下载的路网节点osmid重命名,生成新的节点id;
完整代码#运行环境 Python 3.11
# 导入所需库
import operator # 操作符模块,通常用于自定义排序等操作
import igraph as ig # igraph 图处理库,适用于复杂的图算法和可视化
import networkx as nx # NetworkX 图论库,用于创建和操作复杂网络
import numpy as np # NumPy 数值计算库,提供高性能的多维数组对象
import osmnx as ox # OSMnx 库,用于获取 OpenStreetMap 数据并构建网络图
import matplotlib.pyplot as plt # Matplotlib 数据可视化库,用于绘制图形
import geopandas as gpd # GeoPandas,基于Pandas的地理空间数据处理库
from shapely.geometry import Point, LineString # Shapely 几何对象和操作库
# 设置边的权重属性为“长度”
weight = "length"
# 使用 OSMnx 从 OpenStreetMap 下载厦门市思明区的驾驶网络数据
G_nx = ox.graph_from_place("Siming Qu, Xiamen,Fujian,China", network_type="drive")
# 记录原始网络中所有节点的OSM ID
osmids = list(G_nx.nodes)
# 将NetworkX图中的节点标签(原始OSM ID)转换为从0开始的连续整数,便于后续使用 igraph 处理
G_nx = nx.relabel.convert_node_labels_to_integers(G_nx)
# 构造一个映射关系,将原始OSM ID映射到新的整数标签上
osmid_values = {old: new for old, new in zip(G_nx.nodes, osmids)}
# 将上述映射关系作为节点属性"osmids"存储回NetworkX图中,以便跟踪原始OSM ID
nx.set_node_attributes(G_nx, osmid_values, "osmids")
# 使用 OSMnx 提供的便捷函数保存处理后的网络图到GeoPackage文件
ox.save_graph_geopackage(G_nx, filepath="D:/data/Siming_network.gpkg")如下图所示,展示了新的节点id;
第二步就是选择起终点,soure是起点id,target是终点id,有需要的改一下即可,坐标用的wgs84,可以用这个直接拾取新的坐标地图坐标系转换 - 在线工具 (tool.lu);
# 选择起始节点和目标节点
source = list(G_nx.nodes())[0]
target = list(G_nx.nodes())[2716]路网底图和出行类型需要改的话改这里,出行方式包括'walk'、bike'、'drive';
G_nx = ox.graph_from_place("Siming Qu, Xiamen,Fujian,China", network_type="drive")完整代码#运行环境 Python 3.11
# 导入所需库
import operator
import igraph as ig
import networkx as nx
import numpy as np
import osmnx as ox # 用于获取OpenStreetMap数据
import matplotlib.pyplot as plt # 用于绘图
import geopandas as gpd
from shapely.geometry import Point, LineString
# 设置matplotlib以支持中文显示
plt.rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体
plt.rcParams['axes.unicode_minus'] = False # 保证负号正常显示
# 定义权重属性(本例中为道路长度)
weight = "length"
# 使用osmnx从指定地点(厦门市思明区)获取驾驶网络数据
G_nx = ox.graph_from_place("Siming Qu, Xiamen,Fujian,China", network_type="drive")
# 保存原始节点ID并转换节点标签为整数,以便在igraph中使用
osmids = list(G_nx.nodes)
G_nx = nx.relabel.convert_node_labels_to_integers(G_nx)
osmid_values = {old: new for old, new in zip(G_nx.nodes, osmids)}
nx.set_node_attributes(G_nx, osmid_values, "osmid")
# 创建一个igraph图,添加节点和边,设置边权重和节点的OSM ID属性
G_ig = ig.Graph(directed=True)
G_ig.add_vertices(G_nx.nodes)
G_ig.add_edges(G_nx.edges())
G_ig.vs["osmid"] = osmids
G_ig.es[weight] = list(nx.get_edge_attributes(G_nx, weight).values())
# 使用osmnx绘制原始网络图,设定样式
fig, ax = ox.plot_graph(G_nx, show=False, close=False, edge_color="#999999", edge_alpha=0.5, node_size=0, figsize=(10, 10))
# 选择起始节点和目标节点
source = list(G_nx.nodes())[0]
target = list(G_nx.nodes())[2716]
# 计算最短路径(这里使用NetworkX进行计算)
path2 = nx.shortest_path(G_nx, source, target, weight=weight)
# 获取路径上每个节点的坐标
node_positions = {node: (G_nx.nodes[node]['x'], G_nx.nodes[node]['y']) for node in path2}
# 在图上用红色线条高亮显示最短路径
for i in range(len(path2) - 1):
start_node = node_positions[path2[i]]
end_node = node_positions[path2[i + 1]]
ax.plot([start_node[0], end_node[0]], [start_node[1], end_node[1]], color='r', linewidth=2)
# 设置图表标题并关闭坐标轴,最后展示图形
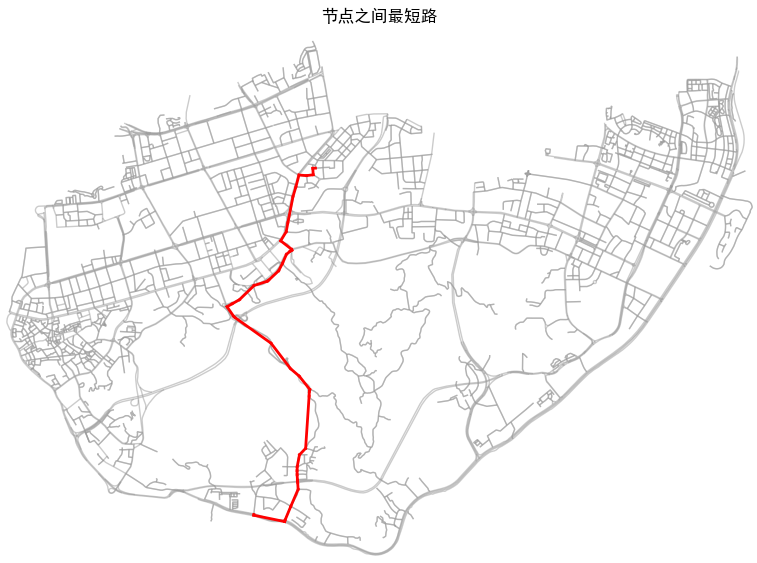
plt.title('节点之间最短路径')
plt.axis('off')
# 指定输出图像的文件路径和名称
output_image_path = "siming_qu_shortest_path.png"
# 保存图表到指定路径,采用高质量的DPI(每英寸点数)以保证图像清晰度,
# 'bbox_inches="tight"'确保保存时不包含多余的空白边缘,
# 'transparent=False'指明图像背景不透明,
# 'facecolor="white"'设定图像背景色为白色,与之前设置保持一致。
plt.savefig(output_image_path, dpi=300, bbox_inches='tight', transparent=False, facecolor='white')
# 在绘制完成后展示图表
plt.show()
# 打印消息告知用户图像已成功保存的路径
print(f"节点之间最短路的图已保存至: {output_image_path}")结果如下图所示,该结果展示了起点【0】到终点【2716】的最短路径,并保存为png格式。
文章仅用于分享个人学习成果与个人存档之用,分享知识,如有侵权,请联系作者进行删除。所有信息均基于作者的个人理解和经验,不代表任何官方立场或权威解读。