一. 欧式距离

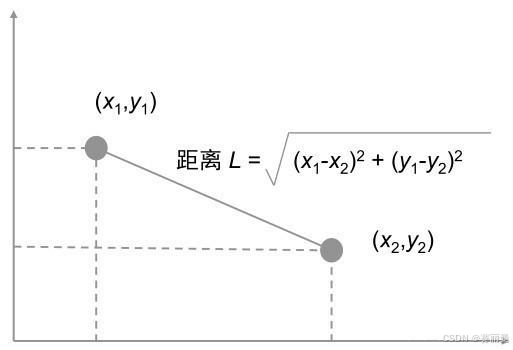
欧式距离（Euclidean distance）:多维空间中两点之间的直线距离

对于两个点 $(A=(x_1,x_2,...,x_n))和(B=(y_1,y_2,...,y_n))$，欧式距离的公式为：

$$d(A,B)=\sqrt{(x_1-y_1{)}^2+(x_2-y_2{)}^2+...+(x_n-y_n{)}^2}$$

在二维空间中（即 ( n = 2 )），欧式距离简化为：

$$d(A,B)=\sqrt{(x_1-y_1{)}^2+(x_2-y_2{)}^2}$$

二. 曼哈顿距离

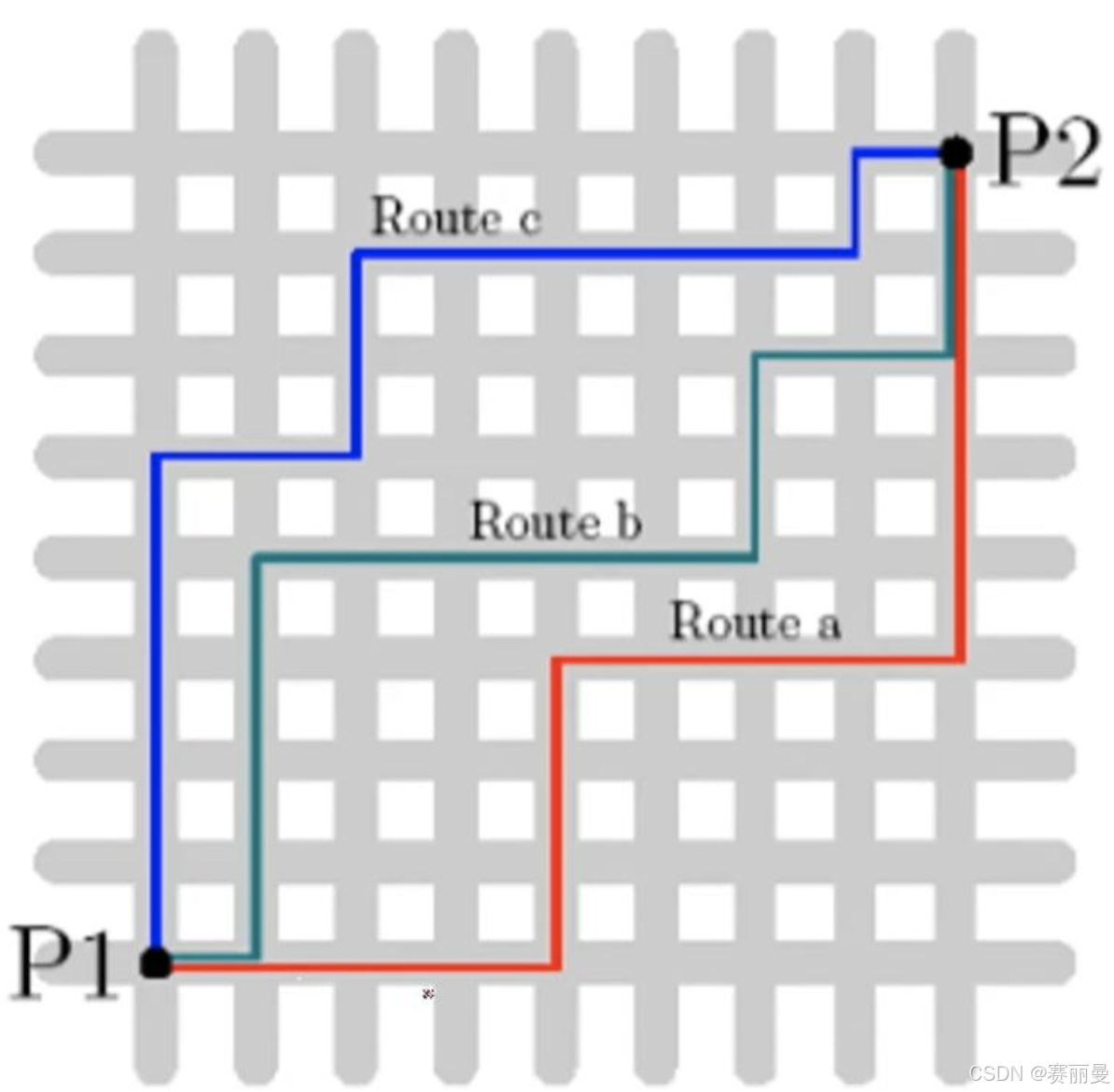
曼哈顿距离，也叫做“城市街区距离”或“L1范数”，度量的是在网格状的空间中，两点之间的总直线距离。它计算的是两个点在各个坐标轴上差值的绝对值之和。

对于两个点 $(A=(x_1,x_2,...,x_n))$和$(B=(y_1,y_2,...,y_n))$，曼哈顿距离的公式为：

$$d(A,B)=|x_1-y_1|+|x_2-y_2|+...+|x_n-y_n|$$

在二维空间中（即 ( n = 2 )），曼哈顿距离简化为：

$$d(A,B)=|x_1-y_1|+|x_2-y_2|$$

三. 切比雪夫距离

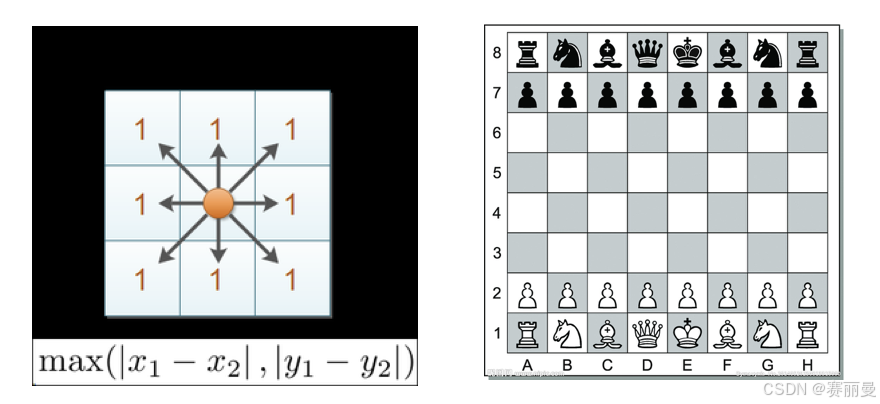
切比雪夫距离度量的是两点之间的最大坐标差。它反映了两点在“棋盘式”格局下的最短路径（即每一步可以沿着坐标轴的任何方向移动）。

对于两个点$(A=(x_1,x_2,...,x_n))$ 和 $(B=(y_1,y_2,...,y_n))$，切比雪夫距离的公式为：

$$d(A,B)=\max (|x_1-y_1|,|x_2-y_2|,...,|x_n-y_n|)$$

在二维空间中（即 ( n = 2 )），切比雪夫距离简化为：

$$d(A,B)=\max (|x_1-y_1|,|x_2-y_2|)$$

四. 闵式距离

闵式距离（Minkowski Distance）是一类距离度量的泛化形式，包括了欧几里得距离、曼哈顿距离和切比雪夫距离等作为特例。闵式距离的一般定义为：

$$d_p={\left(\sum _{i=1}^n|x_i-y_i{|}^p\right)}^{1/p}$$

其中，$(x=(x_1,x_2,\dots ,x_n))$ 和$(y=(y_1,y_2,\dots ,y_n))$是 n 维空间中的两个点，$(p)$ 是一个正数，称为距离的阶数（也可以称为“闵式指数”）。闵式距离的定义可以通过不同的 $(p)$ 值得到不同的距离度量。

1. p不同取值,表示不同距离

• 当 ( p = 1 ) 时，闵式距离变为曼哈顿距离（L1距离）：
  $$d_1=\sum _{i=1}^n|x_i-y_i|$$
• 当 ( p = 2 ) 时，闵式距离变为欧几里得距离（L2距离）：
  $$d_2={\left(\sum _{i=1}^n|x_i-y_i{|}^2\right)}^{1/2}$$
• 当 $(p\to \infty )$ 时，闵式距离变为切比雪夫距离：
  $$d_{\infty }=\underset{i}{\max }|x_i-y_i|$$

2. 当 $(p\to \infty )$ 时，为什么闵式距离变为切比雪夫距离

闵式距离通过参数 $(p)$ 控制了度量的敏感度。随着 $(p)$ 的增大，度量对坐标差异较大的维度会变得更加敏感。当 $(p)$ 趋近于无穷大时，闵式距离就转化为切比雪夫距离，关注的是最大的坐标差异。

我们可以考虑闵式距离在 $(p\to \infty )$ 时的极限行为。假设我们有 $(n)$ 个坐标差 $(|x_i-y_i|)$ 对应于 $(i=1,2,\dots ,n)$。

当 $(p)$ 增加时，$(|x_i-y_i{|}^p)$ 对较大的坐标差更加敏感。为了更清楚地说明这一点，假设我们有以下几个差值：

$$|x_1-y_1|=3,|x_2-y_2|=1,|x_3-y_3|=2$$

随着 $(p)$增大，$(|x_1-y_1{|}^p=3^p)$会迅速增大，而 $(|x_2-y_2{|}^p=1^p=1)$和 $(|x_3-y_3{|}^p=2^p)$ 的增长速度远低于$(3^p)$。因此，$(|x_1-y_1{|}^p)$ 在总和中占据主导地位。此时，整体的距离更依赖于最大值的坐标差，而对小的坐标差的贡献可以忽略不计。(开方为递增函数,可以削弱趋势,但改变不了趋势)

因此，当 $(p\to \infty )$ 时，闵式距离的计算会变为：

$$d_{\infty }=\underset{i}{\max }|x_i-y_i|$$

也就是说，闵式距离的极限值就是所有坐标差中的最大值，这正是切比雪夫距离的定义。

当 $(p\to \infty )$ 时，闵式距离变为切比雪夫距离的原因是：在极大的 $(p)$ 下，较大的坐标差主导了距离的计算，而较小的坐标差对总和的贡献变得微不足道，从而使得闵式距离的计算结果转化为最大坐标差，即切比雪夫距离。

五. 总结

• 欧几里得距离：沿直线的最短路径
• 曼哈顿距离：移动只能沿着水平或垂直方向。
• 切比雪夫距离：考虑沿任何方向的最大移动步数。
• 闵式距离：一类距离度量的泛化形式

每种距离度量有不同的应用场景，选择合适的度量方式取决于具体问题的需求。