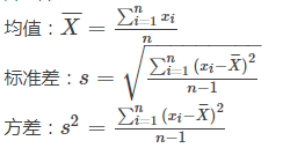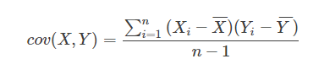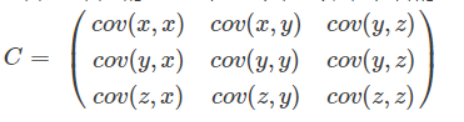几个概念

解释方差

当有多个变量,分析单个变量与总方差的方差比。

方差

描述波动情况

协方差

x,y的相关性

协方差矩阵

最大重构性

找到一个超平面使得样本点在这个超平面的投影尽量分开。

去中心化

使数据满足均值为0，但对标准差没有要求。

过度拟合

欠拟合：如果一个算法没有很好的拟合数据，比如一个本应该用二次多项式拟合的数据用了线性去拟合，导致最后拟合数据的效果很差。我们称之为欠拟合（underfitting）或者高偏差（high bias）。
过拟合：如果一个应该用二次多项式去拟合的数据用了四次多项式甚至更高次，在拟合这些数据的时候可能表现的很好，使得代价函数很低。但其实并不是一个好的模型，只要加入新的数据就有极大的可能性不匹配需要重新拟合。这种情况叫做过拟合（overfitting）或者高方差（high variance）。数据中存在着一些噪声，高阶多项式去拟合数据的时候将这些噪声也考虑进去，即尽可能的去拟合这些噪声点，使得代价函数非常的低甚至接近于0，最后拟合出来的模型“歪歪扭扭”，对应高阶多项式的图像，但是非常“脆弱不堪”，一旦有在边界上的数据出现，就会表现的很差。
什么时候出现过拟合：特征太多而训练数据太少的时候

最大方差理论

最好的k维特征是将n维样本点转换为k维后，每一维上的样本方差都很大。
因为投影后的样本点之间方差最大（也可以说是投影的绝对值之和最大）
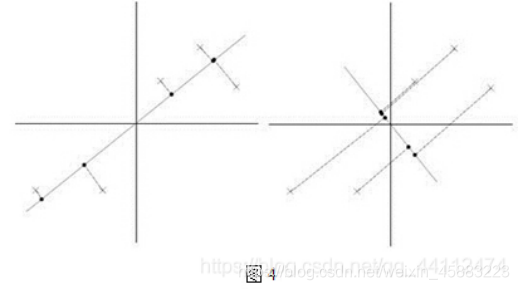
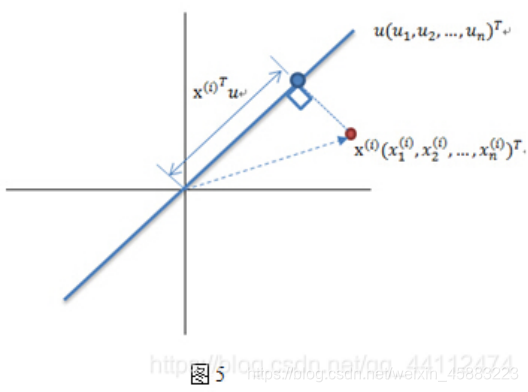
把二维降为一维如果方差不大那么就会在主方向轴投影点会重叠，损失信息很大，并且丢失的向量是很重要的。（图4，5数据过原点已经数据中心化）图4的左半部分是最优的
在u>x,u为主向量时。我们可以看到点在u上的投影和u和u的正交向量有关。显然图4左边的投影面比右边的大并且投影点之间的方差大。图五是图四的单个点细节图。

原理

主成分分析是一个统计过程，该过程通过正交变换将原始的 n 维数据集变换到一个新的被称做主成分的数据集中。本质是一种向上提取的方法。主成分分析通过累计的解释方差之和来判断主成分对所有特征的解释程度。
变换后的结果中，第一个主成分具有最大的方差值，每个后续的成分在与前述主成分正交条件限制下具有最大方差。降维时仅保存前 m(m < n) 个主成分即可保持最大的数据信息量。
主要思想：把数据从原来的坐标系转换到新的坐标系，新坐标系的选择由数据本身决定：第一个新坐标轴选择的是原始数据中方差最大的方向，第二个新坐标轴选择和第一个坐标轴正交且具有方差次大的方向。第二个选取的方向应该和第一个方向具有很弱的相关性。
此过程一直重复，重复次数为原始数据中特征的数目。大部分方差都集中在最前面的几个新坐标轴中。因此，可以忽略剩下的坐标轴，即对数据进行了降维处理。

PCA也可以看作是逐一筛选方差最大方向；对协方差矩阵XX^T特征分解，取最大特征值及其特征向量；在去掉该特征值以及特征向量后，继续取最大特征值；
投影方向应该取多少才好？
选取特征值和占总特征值的80%
PCA为什么需要去中心化？
根据方差公式，如果没有事先进行去中心化后，在计算过程中也会去减去均值，增大计算复杂度

注意点

（1）特征根的大小决定了我们感兴趣信息的多少。即小特征根往往代表了噪声，但实际上，向小一点的特征根方向投影也有可能包括我们感兴趣的数据；
（2）特征向量的方向是互相正交（orthogonal）的，这种正交性使得PCA容易受到Outlier的影响
（3）PCA适用于非监督的学习的不带标签(带标签的样本，往往用LDA降维)的样本降维，特别是小样本问题。广义认为，这类样本属性之间的相关性很大，通过映射，将高维样本向量映射成属性不相关的样本向量。
（4）PCA是一个去属性相关性的过程，这里的相关性主要指的是线性相关性

步骤

1.原始数据处理（减去均值）
把数据中心化，减少过度拟合的可能性。
2.求协方差矩阵
3.求特征值和特征向量
特征向量代表坐标系，特征值代表映射到新坐标的长度然后做数据转换。
4.选取最大k个特征值对应的特征向量(其中k是小于维度总数的一个值)：
(1)将特征值按照从大到小的顺序排序
(2)选择其中最大的k个
(3)将其对应的k个特征向量分别作为列向量组成特征向量矩阵

对一个n * n的对称矩阵进行分解，我们可以求出它的特征值和特征向量，就会产生n个n维的正交基，每个正交基会对应一个特征值。然后把矩阵投影到这N个基上，此时特征值的模就表示矩阵在该基的投影长度。
特征值越大，说明矩阵在对应的特征向量上的方差越大，样本点越离散，越容易区分，信息量也就越多。因此，特征值最大的对应的特征向量方向上所包含的信息量就越多，如果某几个特征值很小，那么就说明在该方向的信息量非常少，我们就可以删除小特征值对应方向的数据，只保留大特征值方向对应的数据，这样做以后数据量减小，但有用的信息量都保留下来了。

总结

1.去除平均值
2.计算协方差矩阵
3.计算协方差矩阵的特征值和特征向量
4.特征值从大到小排序
5.保留最上面k个特征向量
6.将数据转换到k个向量构建的新空间中
7.n维矩阵*k维特征向量=k维矩阵
为了说明什么是数据的主成分，先从数据降维说起。假设三维空间中有一系列点，这些点分布在一个过原点的斜面上，如果你用自然坐标系x,y,z这三个轴来表示这组数据的话，需要使用三个维度，而事实上，这些点的分布仅仅是在一个二维的平面上，问题出在哪里？把x,y,z坐标系旋转一下，使数据所在平面与x,y平面重合如果把旋转后的坐标系记为x’,y’,z’，那么这组数据的表示只用x’和y’两个维度表示即可。当然了，如果想恢复原来的表示方式，那就得把这两个坐标之间的变换矩阵存下来。这样就能把数据维度降下来了。

但是，我们要看到这个过程的本质，如果把这些数据按行或者按列排成一个矩阵，那么这个矩阵的秩就是2。这些数据之间是有相关性(有非零解)的，这些数据构成的过原点的向量的最大线性无关组包含2个向量，这就需要平面过原点的。这就是数据中心化的缘故。将坐标原点平移到数据中心，这样原本不相关的数据在这个新坐标系中就有相关性了。增加基向量的正交性。有趣的是，三点一定共面，也就是说三维空间中任意三点中心化后都是线性相关的，一般来讲n维空间中的n个点一定能在一个(n-1)维子空间中分析。n维欧氏空间中余维度等于1的线性子空间，也就是必须是(n-1)维度。这是平面中的直线、空间中的平面之推广。

python例子

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt  # 2D绘图库


# 计算均值,要求输入数据为numpy的矩阵格式，行表示样本数，列表示特征
def meanX(dataX):
    return np.mean(dataX, axis=0)  # axis=0表示按照列来求均值，如果输入list,则axis=1


def pca(XMat, k):
    average = meanX(XMat)
    m, n = np.shape(XMat)
    avgs = np.tile(average, (m, 1))
    data_adjust = XMat - avgs
    covX = np.cov(data_adjust.T)  # 计算协方差矩阵
    featValue, featVec = np.linalg.eig(covX)  # 求解协方差矩阵的特征值和特征向量
    index = np.argsort(-featValue)  # 按照featValue进行从大到小排序
    if k > n:
        print("k must lower than feature number")
        return
    else:
        # 注意特征向量时列向量，而numpy的二维矩阵(数组)a[m][n]中，a[1]表示第1行值
        selectVec = np.matrix(featVec.T[index[:k]])  # 所以这里需要进行转置
        finalData = data_adjust * selectVec.T
        reconData = (finalData * selectVec) + average
    return finalData, reconData


# 输入文件的每行数据都以\t隔开
def loaddata(datafile):
    return np.array(pd.read_csv(datafile, sep=" ", header=None)).astype(np.float)


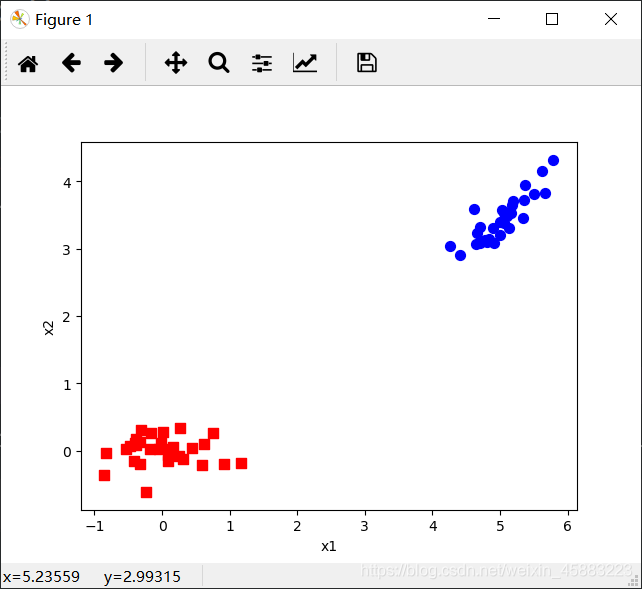
def plotBestFit(data1, data2):
    dataArr1 = np.array(data1)
    dataArr2 = np.array(data2)
    m = np.shape(dataArr1)[0]
    axis_x1 = []
    axis_y1 = []
    axis_x2 = []
    axis_y2 = []
    for i in range(m):
        axis_x1.append(dataArr1[i, 0])
        axis_y1.append(dataArr1[i, 1])
        axis_x2.append(dataArr2[i, 0])
        axis_y2.append(dataArr2[i, 1])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(axis_x1, axis_y1, s=50, c='red', marker='s')
    ax.scatter(axis_x2, axis_y2, s=50, c='blue')
    plt.xlabel('x1')
    plt.ylabel('x2')
    plt.savefig("outfile.png")
    plt.show()


# 根据数据集data.txt
def main():
    datafile = "data.txt"
    XMat = loaddata(datafile)
    k = 2
    return pca(XMat, k)


if __name__ == "__main__":
    finalData, reconMat = main()
    plotBestFit(finalData, reconMat)

5.1 3.5 1.4 0.2
4.9 3.0 1.4 0.2
4.7 3.2 1.3 0.2
4.6 3.1 1.5 0.2
5.0 3.6 1.4 0.2
5.4 3.9 1.7 0.4
4.6 3.4 1.4 0.3
5.0 3.4 1.5 0.2
4.4 2.9 1.4 0.2
4.9 3.1 1.5 0.1
5.4 3.7 1.5 0.2
4.8 3.4 1.6 0.2
4.8 3.0 1.4 0.1
4.3 3.0 1.1 0.1
5.8 4.0 1.2 0.2
5.7 4.4 1.5 0.4
5.4 3.9 1.3 0.4
5.1 3.5 1.4 0.3
5.7 3.8 1.7 0.3
5.1 3.8 1.5 0.3
5.4 3.4 1.7 0.2
5.1 3.7 1.5 0.4
4.6 3.6 1.0 0.2
5.1 3.3 1.7 0.5
4.8 3.4 1.9 0.2
5.0 3.0 1.6 0.2
5.0 3.4 1.6 0.4
5.2 3.5 1.5 0.2
5.2 3.4 1.4 0.2
4.7 3.2 1.6 0.2
4.8 3.1 1.6 0.2

np.mean

求取均值
经常操作的参数为axis，以m * n矩阵举例：

axis 不设置值：对 mn 个数求均值，返回一个实数
axis = 0：压缩行，对各列求均值，返回 1 n 矩阵
axis =1 ：压缩列，对各行求均值，返回 m *1 矩阵

a = np.array([[1, 2], [3, 4], [2, 6]])
# 计算整个数据的平均值
print(a.mean()) # 3

# 计算每一列的平均值
print(a.mean(axis=0)) # [2. 4.]

# 计算每一行的平均值
print(a.mean(axis=1)) # [1.5 3.5 4. ]

np.shape

查看矩阵或数组的维数

np.tile

>>> from numpy import *
>>> a = array([1, 2, 3])
>>> b = tile(a, 2)
>>> b
array([1, 2, 3, 1, 2, 3])
>>> c = tile(a, (2, 3))
>>> c
array([[1, 2, 3, 1, 2, 3, 1, 2, 3],
       [1, 2, 3, 1, 2, 3, 1, 2, 3]])

np.cov

计算协方差矩阵

np.linalg.eig

计算矩阵的特征值和特征向量

np.argsort

数组排序

plt.figure

创建一个新的画板

add_subplot plt.subplot

将画布分成x * y的块，这个图在第i个块上显示

scatter

绘制散点图

plt.xlabel plt.ylabel

设置坐标轴的标签文本

import numpy as np
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt


def pca(data, n_dim):
    data = data - np.mean(data, axis=0, keepdims=True)
    cov = np.dot(data.T, data)
    eig_values, eig_vector = np.linalg.eig(cov)
    # print(eig_values)
    indexs_ = np.argsort(-eig_values)[:n_dim]
    picked_eig_vector = eig_vector[:, indexs_]
    data_ndim = np.dot(data, picked_eig_vector)
    return data_ndim


# data 降维的矩阵(n_samples, n_features)
# n_dim 目标维度
# fit n_features >> n_samples, reduce cal
def highdim_pca(data, n_dim):
    N = data.shape[0]
    data = data - np.mean(data, axis=0, keepdims=True)
    Ncov = np.dot(data, data.T)
    Neig_values, Neig_vector = np.linalg.eig(Ncov)
    indexs_ = np.argsort(-Neig_values)[:n_dim]
    Npicked_eig_values = Neig_values[indexs_]
    # print(Npicked_eig_values)
    Npicked_eig_vector = Neig_vector[:, indexs_]
    # print(Npicked_eig_vector.shape)
    picked_eig_vector = np.dot(data.T, Npicked_eig_vector)
    picked_eig_vector = picked_eig_vector / (N * Npicked_eig_values.reshape(-1, n_dim)) ** 0.5
    # print(picked_eig_vector.shape)
    data_ndim = np.dot(data, picked_eig_vector)
    return data_ndim


if __name__ == "__main__":
    data = load_iris()
    X = data.data
    Y = data.target
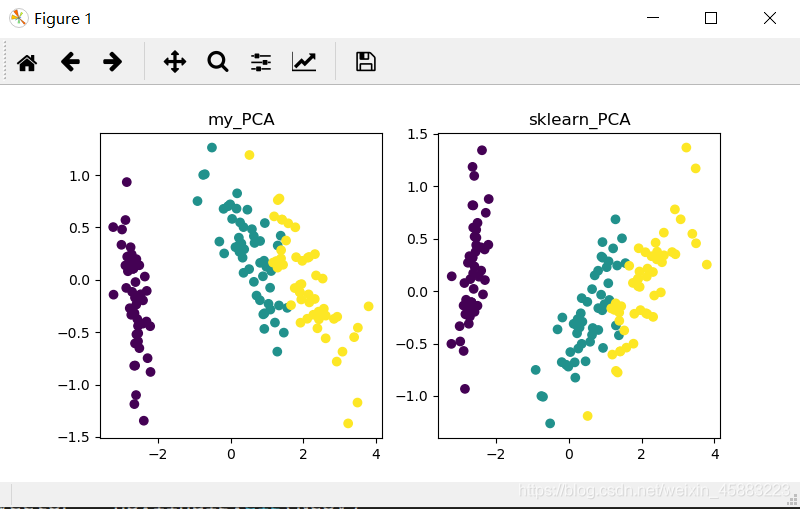
    data_2d1 = pca(X, 2)
    plt.figure(figsize=(8, 4))
    plt.subplot(121)
    plt.title("my_PCA")
    plt.scatter(data_2d1[:, 0], data_2d1[:, 1], c=Y)
    sklearn_pca = PCA(n_components=2)
    data_2d2 = sklearn_pca.fit_transform(X)
    plt.subplot(122)
    plt.title("sklearn_PCA")
    plt.scatter(data_2d2[:, 0], data_2d2[:, 1], c=Y)
    plt.show()

np.dot

计算向量内积

load_iris

Iris数据集在模式识别研究领域应该是最知名的数据集了，有很多文章都用到这个数据集。这个数据集里一共包括150行记录，其中前四列为花萼长度，花萼宽度，花瓣长度，花瓣宽度等4个用于识别鸢尾花的属性，第5列为鸢尾花的类别（包括Setosa，Versicolour，Virginica三类）。也即通过判定花萼长度，花萼宽度，花瓣长度，花瓣宽度的尺寸大小来识别鸢尾花的类别。
这里使用数据集的data、target两个属性进行机器学习的训练
这里data为训练所需的数据集，target为数据集对应的分类标签，属于监督学习

sklearn_pca.fit_transform

fit_transform是fit和transform的组合，既包括了训练又包含了转换。
transform()和fit_transform()二者的功能都是对数据进行某种统一处理（比如标准化~N(0,1)，将数据缩放(映射)到某个固定区间，归一化，正则化等）
fit_transform(trainData)对部分数据先拟合fit，找到该part的整体指标，如均值、方差、最大值最小值等等（根据具体转换的目的），然后对该trainData进行转换transform，从而实现数据的标准化、归一化等等。

from sklearn import datasets
import matplotlib.pyplot as plt
import numpy as np


def shuffle_data(X, y, seed=None):
    if seed:
        np.random.seed(seed)
    idx = np.arange(X.shape[0])
    np.random.shuffle(idx)
    return X[idx], y[idx]


# 正规化数据集 X
def normalize(X, axis=-1, p=2):
    lp_norm = np.atleast_1d(np.linalg.norm(X, p, axis))
    lp_norm[lp_norm == 0] = 1
    return X / np.expand_dims(lp_norm, axis)


# 标准化数据集 X
def standardize(X):
    X_std = np.zeros(X.shape)
    mean = X.mean(axis=0)
    std = X.std(axis=0)
    # 做除法运算时请永远记住分母不能等于0的情形
    # X_std = (X - X.mean(axis=0)) / X.std(axis=0)
    for col in range(np.shape(X)[1]):
        if std[col]:
            X_std[:, col] = (X_std[:, col] - mean[col]) / std[col]
    return X_std


# 划分数据集为训练集和测试集
def train_test_split(X, y, test_size=0.2, shuffle=True, seed=None):
    if shuffle:
        X, y = shuffle_data(X, y, seed)
    n_train_samples = int(X.shape[0] * (1 - test_size))
    x_train, x_test = X[:n_train_samples], X[n_train_samples:]
    y_train, y_test = y[:n_train_samples], y[n_train_samples:]
    return x_train, x_test, y_train, y_test


# 计算矩阵X的协方差矩阵
def calculate_covariance_matrix(X, Y=np.empty((0, 0))):
    if not Y.any():
        Y = X
    n_samples = np.shape(X)[0]
    covariance_matrix = (1 / (n_samples - 1)) * (X - X.mean(axis=0)).T.dot(Y - Y.mean(axis=0))
    return np.array(covariance_matrix, dtype=float)


# 计算数据集X每列的方差
def calculate_variance(X):
    n_samples = np.shape(X)[0]
    variance = (1 / n_samples) * np.diag((X - X.mean(axis=0)).T.dot(X - X.mean(axis=0)))
    return variance


# 计算数据集X每列的标准差
def calculate_std_dev(X):
    std_dev = np.sqrt(calculate_variance(X))
    return std_dev


# 计算相关系数矩阵
def calculate_correlation_matrix(X, Y=np.empty([0])):
    # 先计算协方差矩阵
    covariance_matrix = calculate_covariance_matrix(X, Y)
    # 计算X, Y的标准差
    std_dev_X = np.expand_dims(calculate_std_dev(X), 1)
    std_dev_y = np.expand_dims(calculate_std_dev(Y), 1)
    correlation_matrix = np.divide(covariance_matrix, std_dev_X.dot(std_dev_y.T))
    return np.array(correlation_matrix, dtype=float)


class PCA():
    """
    主成份分析算法PCA，非监督学习算法.
    """

    def __init__(self):
        self.eigen_values = None
        self.eigen_vectors = None
        self.k = 2

    def transform(self, X):
        """
        将原始数据集X通过PCA进行降维
        """
        covariance = calculate_covariance_matrix(X)
        # 求解特征值和特征向量
        self.eigen_values, self.eigen_vectors = np.linalg.eig(covariance)
        # 将特征值从大到小进行排序，注意特征向量是按列排的，即self.eigen_vectors第k列是self.eigen_values中第k个特征值对应的特征向量
        idx = self.eigen_values.argsort()[::-1]
        eigenvectors = self.eigen_vectors[:, idx][:, :self.k]
        # 将原始数据集X映射到低维空间
        X_transformed = X.dot(eigenvectors)
        return X_transformed


def main():
    # Load the dataset
    data = datasets.load_iris()
    X = data.data
    y = data.target
    # 将数据集X映射到低维空间
    X_trans = PCA().transform(X)
    x1 = X_trans[:, 0]
    x2 = X_trans[:, 1]
    cmap = plt.get_cmap('viridis')
    colors = [cmap(i) for i in np.linspace(0, 1, len(np.unique(y)))]
    class_distr = []
    # Plot the different class distributions
    for i, l in enumerate(np.unique(y)):
        _x1 = x1[y == l]
        _x2 = x2[y == l]
        _y = y[y == l]
        class_distr.append(plt.scatter(_x1, _x2, color=colors[i]))
    # Add a legend
    plt.legend(class_distr, y, loc=1)
    # Axis labels
    plt.xlabel('Principal Component 1')
    plt.ylabel('Principal Component 2')
    plt.show()


if __name__ == "__main__":
    main()

np.random.seed

设置随机数种子

np.arange

生成一个从start（包含）到stop（不包含），以step为步长的序列。返回一个ndarray对象。
可以生成整型、浮点型序列，毫无压力。
当step参数为非整数时（如step=0.1），结果往往不一致。对于这些情况，最好使用“linspace()”函数。

参数含义：
start：数值型，可选填。包含此值。默认为0。
stop：数值型，必填。不包含此值。除非step的值不是整数，浮点舍入会影响“out”的长度。
step：数值型，可选填。默认为1，如果步长有指定，则start必须给出来。
dtype：数据类型。输出的array数据类型。如果未指定dtype，则输出的array类型由其它的输入参数决定。
start、stop、step若任一个为浮点型，那么都会生成一个浮点型序列。

np.random.shuffle

对已有列表进行打乱

np.atleast_1d

将输入数据直接视为一维

np.linalg.norm

矩阵或向量的范数

np.expand_dims

在相应的axis轴上扩展维度

std

标准差

np.divide

数组对应位置元素做除法。
这里的除法结果和Python传统的地板除不同，这里得到的是真实值。np.divide的计算结果适应于输出值的数值类型，与输入值的数值类型无关。

plt.get_cmap

获取图谱

np.linspace

在指定的间隔内返回均匀间隔的数字。
返回num均匀分布的样本，在[start, stop]。
这个区间的端点可以任意的被排除在外。

np.unique

对于一维数组或者列表，unique函数去除其中重复的元素，并按元素由大到小返回一个新的无元素重复的元组或者列表

plt.legend

给图加上图例