树与图的存储方法(邻接矩阵和前式链向星)

树与图的存储方法一般有两种：

邻接矩阵
邻接表

其中邻接矩阵适合存储稠密图，邻接表适合存储稀疏图。
邻接矩阵：
邻接矩阵是表示顶点之间相邻关系的矩阵，若一个图G有n个节点，那么邻接矩阵A的大小则为n×n，其中定义，若有一点u到v之间有边，则A[u][v]=1,否则为0。
所以邻接矩阵就是一个二维数组，其中下标u,v表示u到v的边，二维数组位于u行v列的值表示存不存在从u到v的边，如果有就为1，没有就为0。
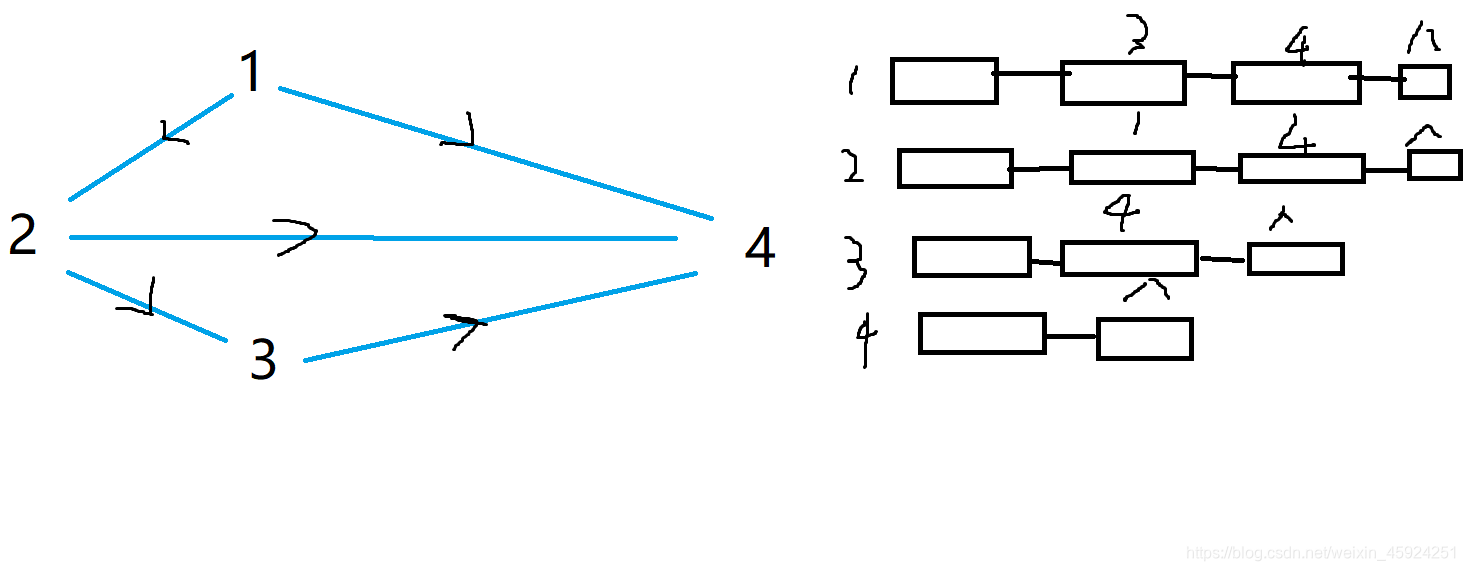
邻接表：
邻接表的本质是n个单链表，看了网上的博客觉得讲的都不是人听的话（~~一定是我太菜了~~ ）。
邻接表的定义：在邻接表中，对图中每一个顶点vi建立一个单链表，把与vi相邻接的顶点放在这个链表中。邻接表中每一个单链表的第一个结点存放有关顶点的信息，把这一节点看成链表的表头，其余节点存放有关边的信息，这样邻接表便由两部分组成，表头结点和边表。
那么对于这部分定义，比较比较关键也是理解建立邻接表的地方在于：表头放存放顶点的信息，其余节点是存放边的信息，也就是说其余的节点要记录边的信息，而不仅仅是与顶点邻接的点的信息，那么要记录边的信息，就需要给边进行编号。
我觉得邻接表中更加核心的应该是边，应该是利用边来存放点，而不是利用点来存放边，但是最终反映的仍然是点和点的邻接关系。
在这里插入图片描述
数据结构定义：

const int N=100;
typedef struct Arcnode//边节点
{
    int adjvex;//该边所指向的顶点的位置
    struct Arcnode *nextarc;//指向下一条边的指针
    int onfo;//和边有关的其他信息（可选择）
}ArcNode;
typedef struct Vnode//顶点信息
{
    int data;//顶点数据
    ArcNode *fristarc;//指向第一条依附该顶点的边的指针
}Vnode;

链式前向星：用数组模拟单链表来构造邻接矩阵
先给出边节点的定义：

struct Edge
{
    int eid;    // 该条边的编号
    int e;      // 该条边的终点
    int w;      // 该条边的权重
    int nxt;    // 下一条邻边的编号
};

用数组去转换：

const int N=1e5+5;
int h[N];//顶点的表头
int e[N*2],ne[N*2],w[N*2],idx;
//idx为边的编号，e为该边终点所指的顶点的值。
//ne下一条临边的编号,w为这条边所带的权

其中以-1为值表示空，表头不为空，表头的值为边的编号，表示依附于表头的边。
理解了上面的内容，应该就能理解单链表了。
那么用单链表建图：

void add(int u,int v,int weight)//从u到v权值为w
{
    e[idx]=v;w[idx]=weight;
    ne[idx]=h[u];h[u]=idx;
    idx++;
}

如果是无向图就插入两次建立起从u-v和从v-u就行，如果是有向图就插入一次从u-v.

树与图的存储方法(邻接矩阵和前式链向星)

悦读