一、朴素模式匹配算法的代码实现

#include<iostream>
using namespace std;

const int MAXLEN=255;	//预定义最大串长为255 

//ch[0]废弃不用 
typedef struct{
	char ch[MAXLEN];	//每个分量存储一个字符 
	int length;			//串的实际长度 
}SString;

int Index(SString S,SString T){
	int k=1;
	int i=k,j=1;
	while(i<=S.length&&j<=T.length){
		if(S.ch[i]==T.ch[j]){
			++i;
			++j;
		}else{
			++k;
			i=k;
			j=1;
		}
	}
	if(j>T.length){
		return k;
	}
	return 0;
} 

int main(){
	return 0;	
} 

二、朴素模式匹配算法的缺点

当某些字串与模式串能部分匹配时，主串的扫描指针 i 经常回溯，导致时间开销增加

最坏时间复杂度O(mn)

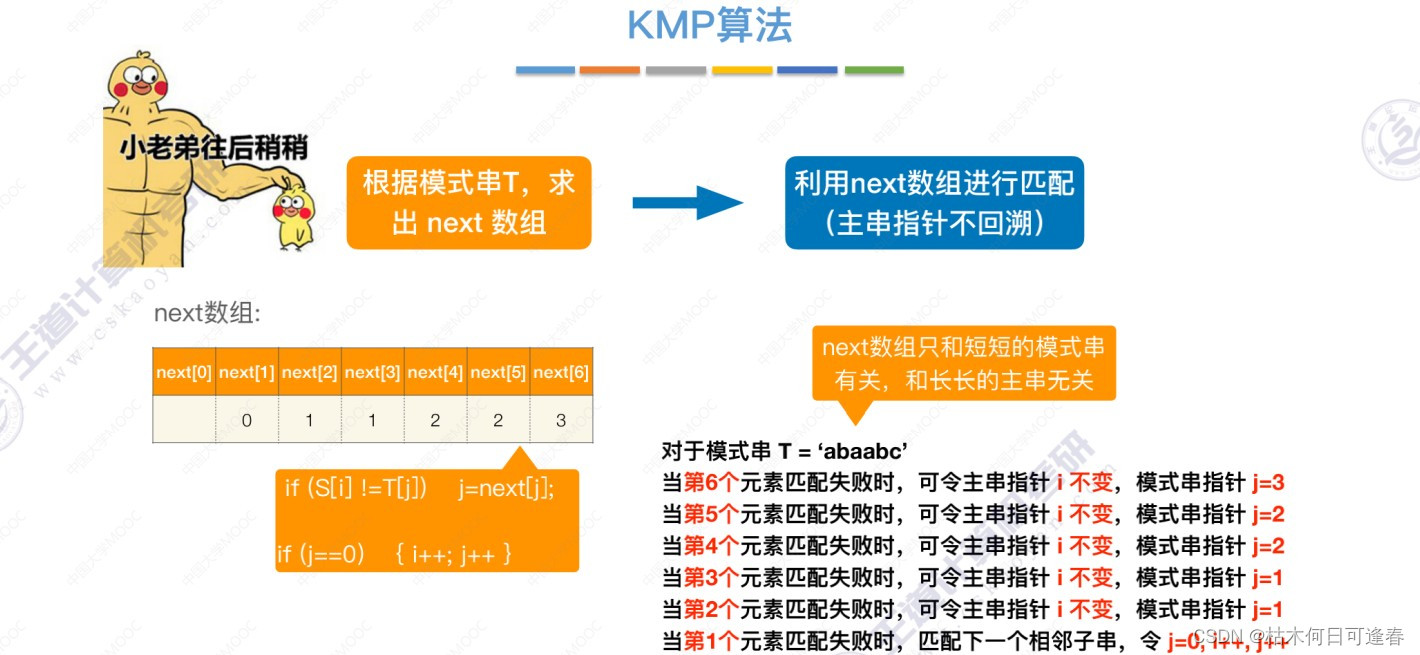
二、KMP算法描述

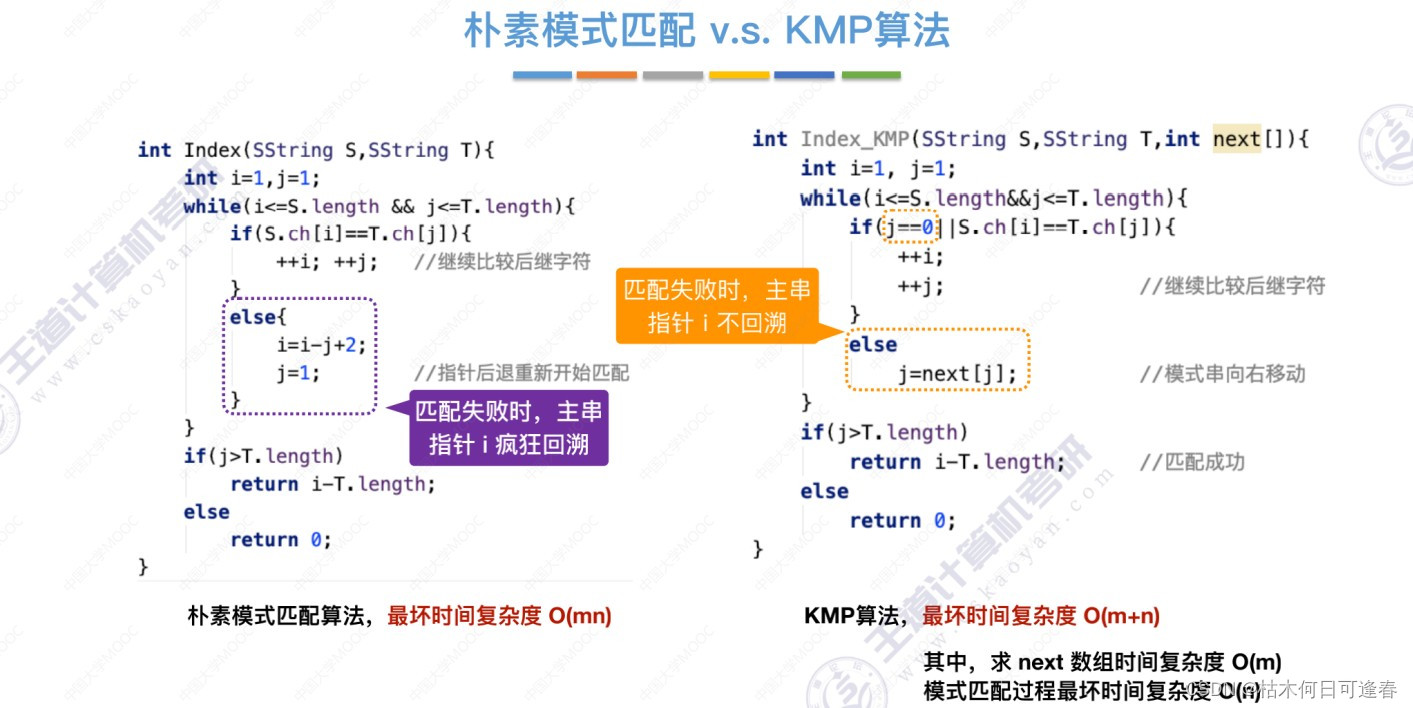
三、朴素模式匹配 vs KMP算法

当字串和模式串不匹配时，主串指针 i 不回溯，模式串指针 j=next[j]

KMP算法时间复杂度O(m+n)，空间复杂度为O(m) （注：主串长n，模式串长m，next数组是针对模式串计算的）

四、求模式串的next数组（手算）

串的前缀：包含第一个字符，且不包含最后一个字符的字串

串的后缀：包含最后一个字符，且不包含第一个字符的字串

next 数组：当模式串的第 j 个字符匹配失败时，令模式串跳到 next[j] 再继续匹配

当第 j 个字符匹配失败，由前 1~j-1 个字符组成的串记为 S ，则：next[j]=S 的最长相等前后缀长度+1

特别地，next[1]=0

注意：在实际KMP算法中，为了使公式更简洁、计算简单，如果串的位序是从1开始的，则next数组才需要整体加1；如果串的位序是从0开始的，则next数组不需要整体加1。

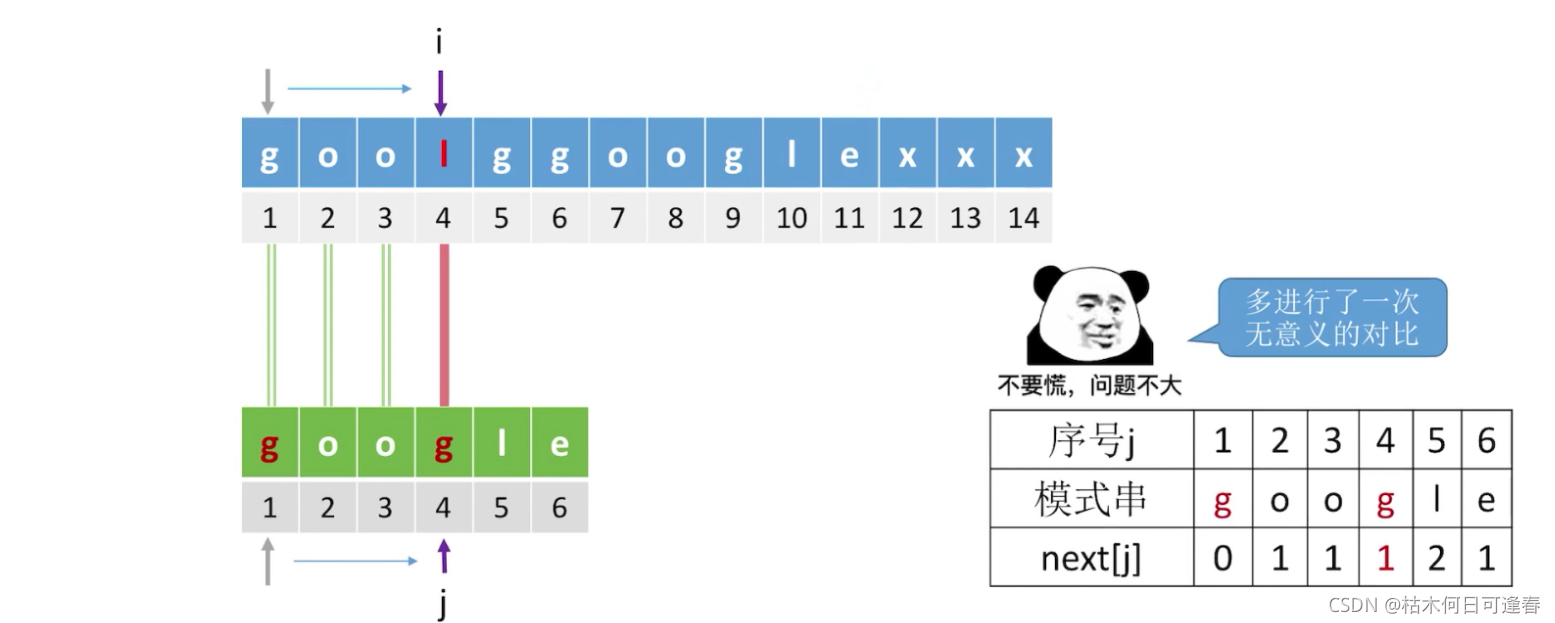
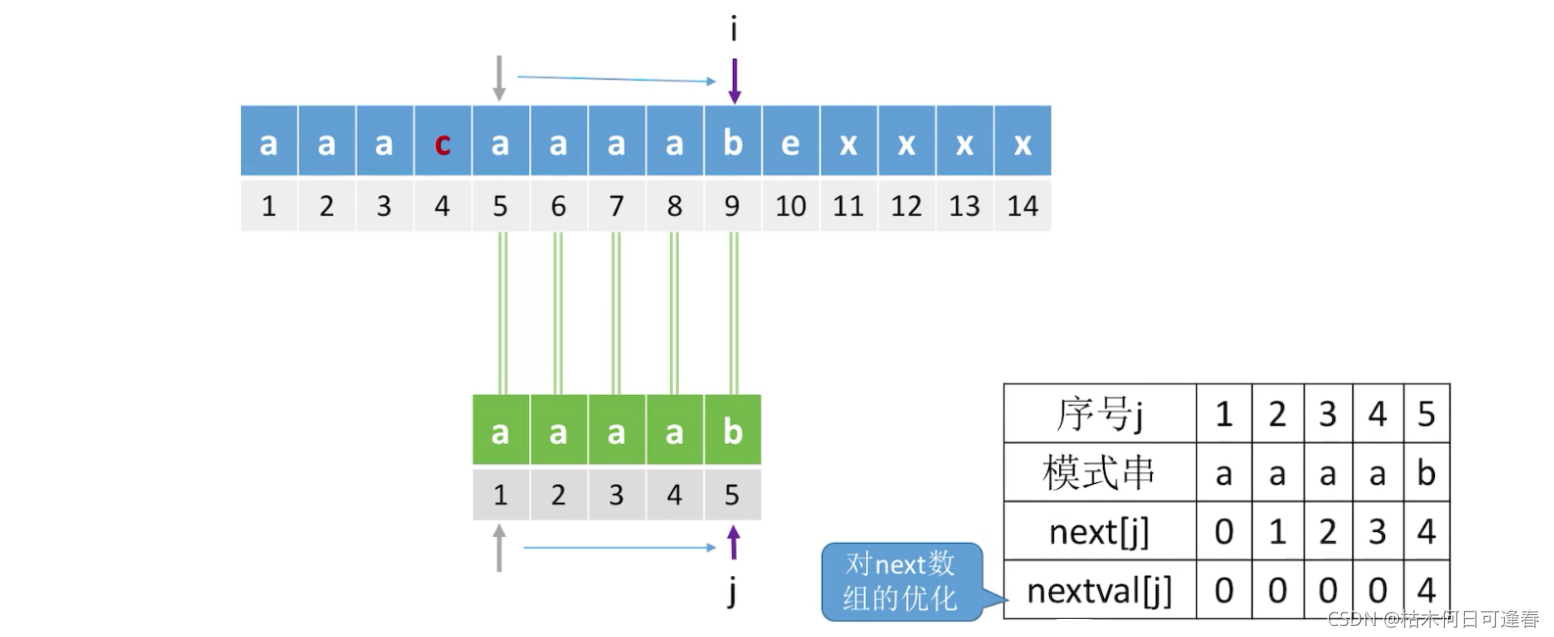
五、KMP算法存在的问题

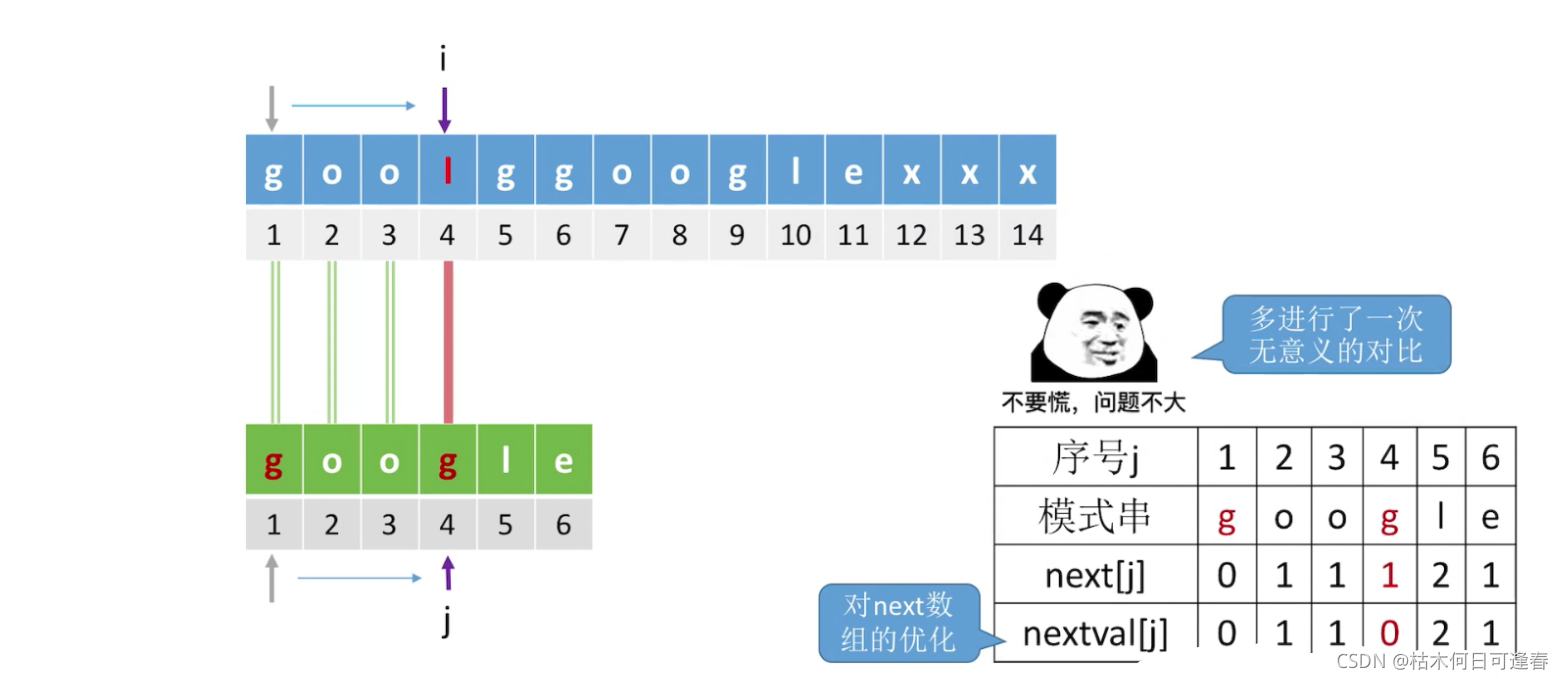
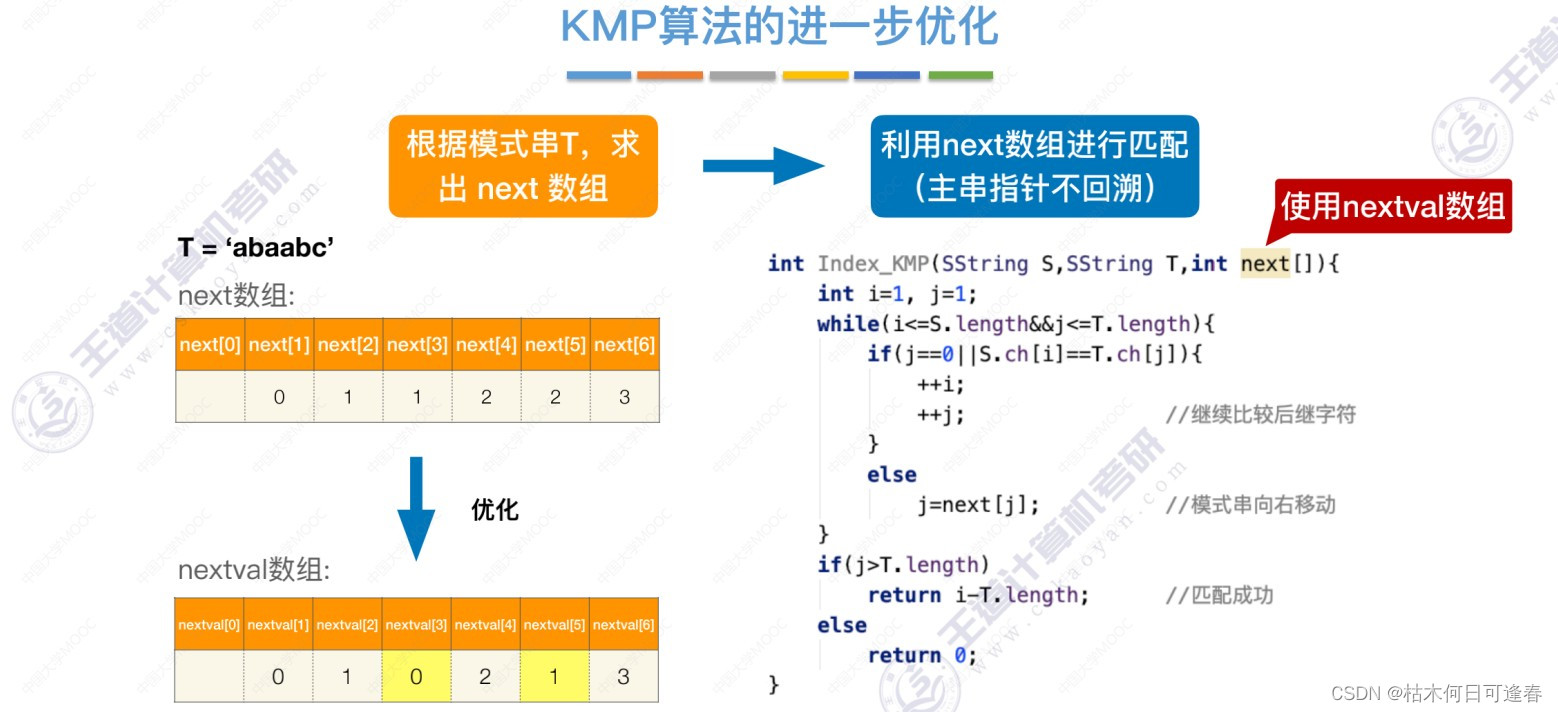
六、KMP算法的进一步优化

七、KMP算法代码完整实现

#include<iostream>
using namespace std;

const int MAXLEN=255;	//预定义最大串长为255 

//ch[0]废弃不用 
typedef struct{
	char ch[MAXLEN];	//每个分量存储一个字符 
	int length;			//串的实际长度 
}SString;

void get_next(SString T,int next[]){
	int i=1,j=0;
	next[1]=0;
	while(i<T.length){
		if(j==0||T.ch[i]==T.ch[j]){
			++i;
			++j; 
			next[i]=j;
		}else{
			j=next[j];
		}
	}
}

void get_nextval(SString T,int next[],int nextval[]){
	nextval[1]=0;
	for(int j=2;j<=T.length;++j){
		if(T.ch[next[j]]==T.ch[j]){
			nextval[j]=nextval[next[j]];
		}else{
			nextval[j]=next[j];
		}
	}
} 

int Index_KMP(SString S,SString T){
	int i=1,j=1;
	int next[T.length+1];
	get_next(T,next);
	int nextval[T.length+1];
	get_nextval(T,next,nextval);
	while(i<=S.length&&j<=T.length){
		if(j==0||S.ch[i]==T.ch[j]){
			++i;
			++j;
		}else{
			j=nextval[j];	//模式串向右移动 
		}
	}
	if(j>T.length){
		return i-T.length;
	}
	return 0;
}

int main(){
	return 0;
} 

八、KMP算法考点总结