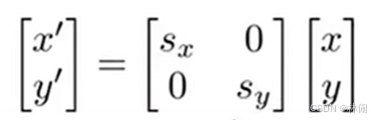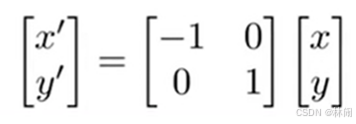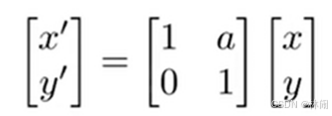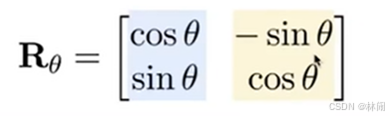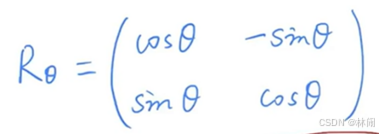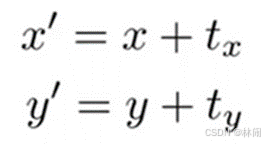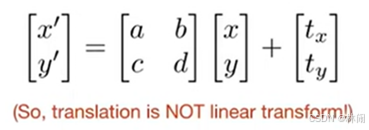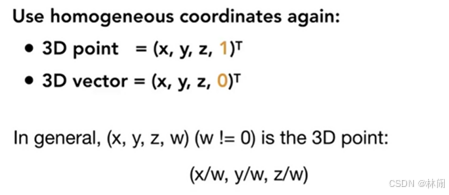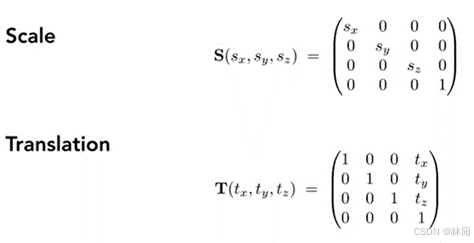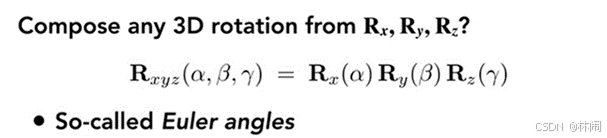目录
1.为什么要学习变换(Why Transformation)
3.2.4 如何表示更复杂的变换:绕三维空间任意一个轴n旋转α角度?
1.为什么要学习变换(Why Transformation)
以下的这些相关工作,都会用到变换的知识,所以我们要学习变换。
1.1 模型变换(Modeling)
摄影机的位置移动
机器人的关节移动
动画中字母I被压扁的过程
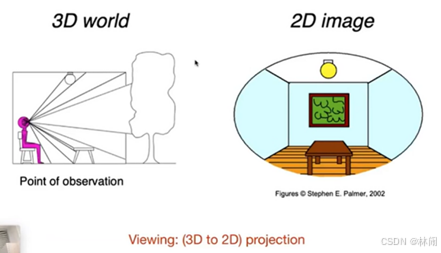
1.2 视图变换(Viewing)
从3D到2D的投影变换
2. 二维仿射变换
仿射变换 = 线性变换 + 平移变换
缩放、旋转属于线性变换,因为这两种变换的坐标原点固定、空间网格不弯曲。
平移操作改变了原点的位置,所以不属于线性变换的范畴。(详见3B1B系列课程)
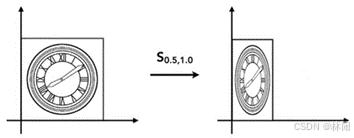
2.1 缩放(scale)
变换矩阵如图,变换后的x坐标变为原来sx的倍,y坐标变为原来的sy倍
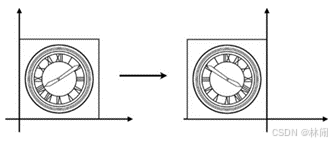
2.1.1 镜像(reflection)
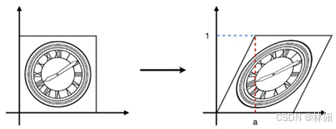
2.1.2 错切(shear)
(1) 错切变换矩阵推导
观察图片变换特点:纵坐标变换前后不变。
观察三个坐标点:
(0,0)移动后变为(0,0);
(0,0.5)移动后变为(0.5*a,0.5);
(0,1)移动后变为(1*a,1)。
总结规律:纵坐标变换前后不变,横坐标都在原来的横坐标基础上加了一个a倍的纵坐标。
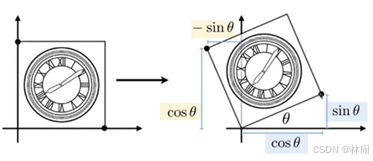
2.2 旋转(rotate)(默认以原点为中心逆时针旋转)
(1)推导方法1:通过两个特殊点构建方程组求解
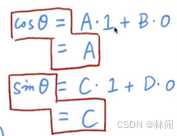
(1,0)变换后为(cosθ,sinθ)
利用此关系可以通过解方程的方式求出变换矩阵中的未知数A与未知数C。

(0,1)变换后为(-sinθ, cosθ)。同理。
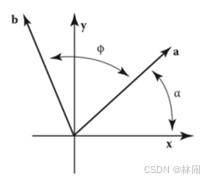
(2)推导方法2:运用极坐标系与直角坐标系的关系
如图,记向量长度为r,则不难得到
将旋转之后的b的坐标x,y用如下表示
将xa,ya的表达式代入,得
此时,利用线性代数知识,不难得出旋转矩阵的结果。
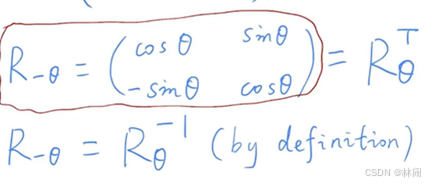
(3)补充:顺时针旋转矩阵=逆时针旋转矩阵的逆=逆时针旋转矩阵的转置:
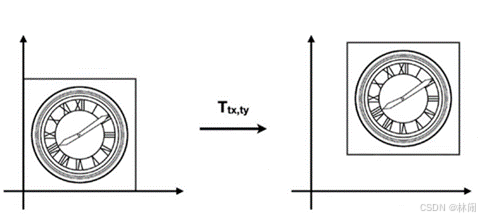
2.3 平移
平移变换不能用矩阵乘以向量的形式表示,它不属于线性变换。
3.齐次坐标
人们不希望将平移变换看作一个单独的、特殊的变换,因为额外处理比较麻烦。
所以,引入了一种将所有仿射变换统一起来的表示方法:齐次坐标
3.1二维齐次坐标
3.1.1 二维齐次坐标的定义
加一个维度,点的第三维是1,向量的第三维是0
齐次坐标下的一些运算规则如图
3.1.2 使用二维齐次坐标表示仿射变换
线性变换:矩阵扩充为3×3,原本2×2的数值不变,第3行、第3列的元素为1,其余新增元素为0。
平移变换:矩阵扩充为3×3,主对角线为1,最后一列、前两行的元素为tx、ty。
3.1.3 使用二维齐次坐标表示复合变换
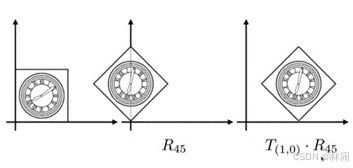
先旋转、后平移才可以达到如图所示的变换结果,特别注意做变换时候的顺序。
矩阵左乘顺序与变换的顺序保持一致
矩阵乘法可以使用结合律,将复合变换的多个变换矩阵浓缩为一个矩阵。
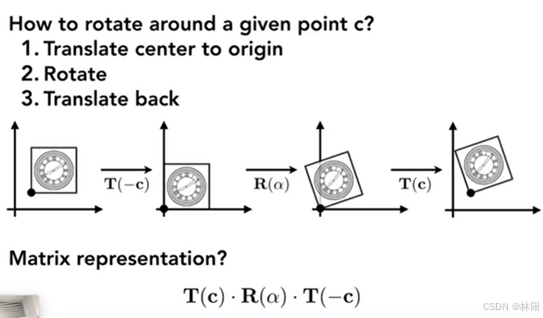
3.1.4 如何表示更复杂的变换:绕平面任意一点c旋转?
先将点c平移到原点,再绕原点旋转,再平移回去。
3.2三维齐次坐标
3.2.1 三维齐次坐标的定义
3.2.2 使用三维齐次坐标表示仿射变换
注意这里4*4的变换矩阵表示的变换顺序是:先线性变换、后平移
缩放变换和平移变换的矩阵与二维齐次坐标下的表示方式类似
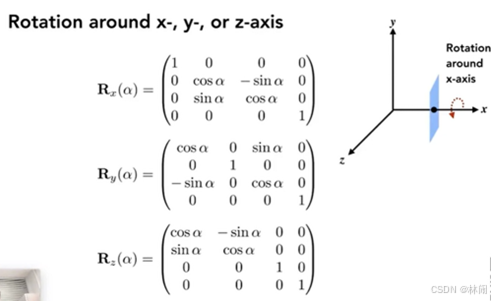
三维空间的旋转变换则相对复杂一些
注意:绕y轴旋转的时候,符号所在的位置与其他两种旋转形式不同,如何理解?
与旋转的方向有关,z叉乘x才得到y。
绕y轴顺时针旋转theta角度 等价于 绕-y轴旋转逆时针旋转-theta角度
把公式角度带成-theta即可,这样想很简单
3.2.3 使用三维齐次坐标表示复合变换
任何一个三维空间的旋转运动都可以分解为绕三个坐标轴分别旋转的操作,或者说,将三个轴的旋转矩阵复合,就可以完成任何一个三维空间中的旋转。
绕每个轴旋转的角度被称为“欧拉角”。
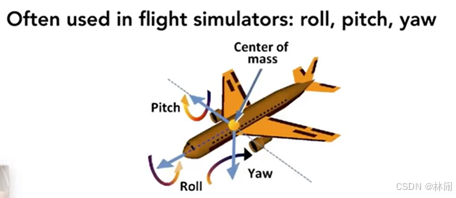
这里常常用飞机飞行的例子来形象地说明
罗德里格斯旋转公式(这里需要找些资料手推一遍)
绕过原点的n轴旋转α角度。
N曾经在向量叉积的表示中出现过
推导过程如下
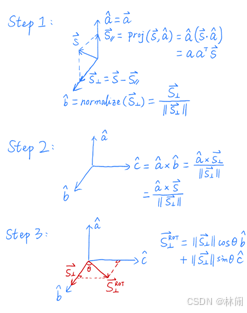
查阅很多资料后,自己写了一下详细的罗德里格斯旋转公式推导过程:
3.2.4 如何表示更复杂的变换:绕三维空间任意一个轴n旋转α角度?
对于,绕不过原点的轴旋转,我们可以借助之前逆矩阵的思想,将解决步骤拆分为
·将旋转轴平移到原点
·绕轴旋转
·再将旋转后的模型平移回去