（一）问题描述
https://leetcode.cn/problems/set-matrix-zeroes/description/?envType=study-plan-v2&envId=top-100-liked示例 1：
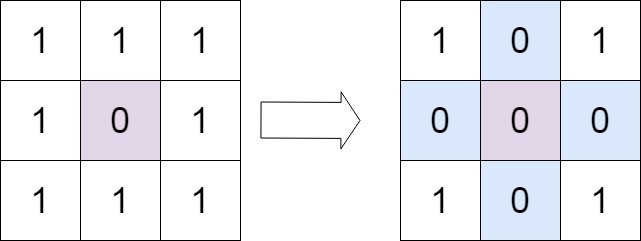
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]] 输出：[[1,0,1],[0,0,0],[1,0,1]]示例 2：
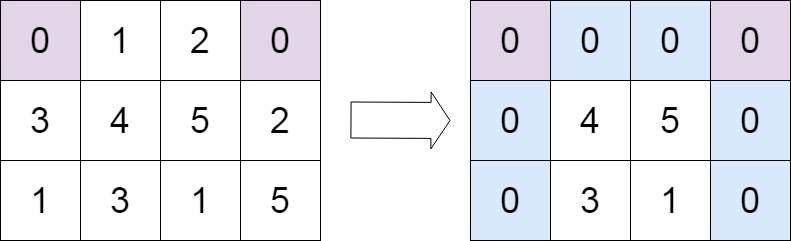
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]] 输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
提示：
m == matrix.lengthn == matrix[0].length1 <= m, n <= 200-231 <= matrix[i][j] <= 231 - 1
进阶：
- 一个直观的解决方案是使用
O(mn)的额外空间，但这并不是一个好的解决方案。 - 一个简单的改进方案是使用
O(m + n)的额外空间，但这仍然不是最好的解决方案。 - 你能想出一个仅使用常量空间的解决方案吗？
（二）解决思路
显然这里要记录哪些行列需要被赋0值。题目要求采用原地算法，即采用固定数量的额外空间，那么就不能才有再开辟一个新的矩阵区域，将修改的元素放到新矩阵里的方式。一种可能的解决方式是维护一个标记矩阵，记录哪些位置需要被赋0值，此时额外空间是O(mn)；另一种可能的解决方式是维护两个标记数组，分别记录哪一行、哪一列需要被赋0值，此时额外空间是O(m+n)。
如果我们想使用常量空间来解决这个问题，可以把两个标记数组省略掉，直接用矩阵的第一行和第一列来标记哪行哪列需要赋0值：遍历矩阵，遇到了0值，就把该位置对应行和列的第一个元素都赋0值作为标记。
但这样就分不清哪些0是原来第一行和第一列里就有的，哪些0是作为标记添加上去的了，因此需要在遍历之前，先维护两个标记变量mFlag和nFlag，用来记录第一行和第一列是否需要赋0值，初始为false：遍历第一行，如果第一行里有0元素，就把mFlag改为true，列和nFlag同理。遍历矩阵做好标记、含有标记的行列赋0值之后，再考察两个标记，如果标记为true就把第一行/第一列赋0值，否则不动。
class Solution {
public void setZeroes(int[][] matrix) {
boolean mFlag=false, nFlag=false;
int m=matrix.length,n=matrix[0].length;
//处理标记变量
for(int i=0;i<m;i++){
if(matrix[i][0]==0){
mFlag=true;
break;
}
}
for(int i=0;i<n;i++){
if(matrix[0][i]==0){
nFlag=true;
break;
}
}
//根据第一行和第一列的标记对行列赋0值
//例如，第一行中的第j位出现了0标记，那么第j列的元素都应该赋0值
for(int i=1;i<m;i++){
for(int j=1;j<n;j++){
if(matrix[i][0]==0||matrix[0][j]==0){
matrix[i][j]=0;
}
}
}
//根据第一行和第一列的标记，判断第一行和第一列是否需要赋0值
if (mFlag) {
for (int i = 0; i < m; i++) {
matrix[i][0] = 0;
}
}
if (nFlag) {
for (int j = 0; j < n; j++) {
matrix[0][j] = 0;
}
}
}
}