（一）问题描述

74. 搜索二维矩阵 - 力扣（LeetCode）74. 搜索二维矩阵 - 给你一个满足下述两条属性的 m x n 整数矩阵： * 每行中的整数从左到右按非严格递增顺序排列。 * 每行的第一个整数大于前一行的最后一个整数。给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。 示例 1：[https://assets.leetcode.com/uploads/2020/10/05/mat.jpg]输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3输出：true示例 2：[https://assets.leetcode-cn.com/aliyun-lc-upload/uploads/2020/11/25/mat2.jpg]输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13输出：false 提示： * m == matrix.length * n == matrix[i].length * 1 <= m, n <= 100 * -104 <= matrix[i][j], target <= 104https://leetcode.cn/problems/search-a-2d-matrix/description/?envType=study-plan-v2&envId=top-100-liked

给你一个满足下述两条属性的 m x n 整数矩阵：

• 每行中的整数从左到右按非严格递增顺序排列。
• 每行的第一个整数大于前一行的最后一个整数。

给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。

示例 1：

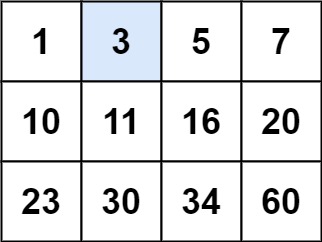
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

示例 2：

输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 100
• -104 <= matrix[i][j], target <= 104

（二）解决思路

        从两个方向使用二分法，先对矩阵的第一列使用二分法，找到最后一个小于等于target的元素，这个元素所在的行就是target可能存在的行，再对这一行使用二分法看能否找到target。

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        //先找在哪行
        int rowNum = matrix.length, colNum = matrix[0].length;
        
        if(target<matrix[0][0]||target>matrix[rowNum-1][colNum-1]) return false;

        int top=0, bottom=matrix.length-1;
        while(top<=bottom){
            int mid = (top+bottom)/2;
            if(target==matrix[mid][0]){
                  return true;
            }
            else if(target<matrix[mid][0]){
                  bottom=mid-1;
            }
            else{
                  top=mid+1;
            }
        }
        //如果第一列找到target这里就返回了，如果没找到，那target可能在的行就是搜索结束时top的前一行
        int row=top-1;

        //在这一行里用二分法判断在不在
        int left = 0, right = colNum-1;
        while(left<=right){
            int mid = (left+right)/2;
            if(target==matrix[row][mid]){
                return true;
            }
            else if(target<matrix[row][mid]){
                right=mid-1;
            }
            else{
                left=mid+1;
            }
        }
        return false;
    }

}