项目设计的目的

利用A*算法实现迷宫寻路功能，利用启发式函数的编写以及各类启发式函数效果的比较。

相关原理知识介绍

A*（A-Star)算法是一种静态路网中求解最短路最有效的方法。公式表示为：f(n)=g(n)+h(n)，其中f(n)是节点n从初始点到目标点的估价函数，g(n)是在状态空间中从初始节点到n节点的实际代价，h(n)是从n到目标节点最佳路径的估计代价。保证找到最短路径（最优解的）条件，关键在于估价函数h(n)的选取：估价值h(n)小于等于n到目标节点的距离实际值，这种情况下，搜索的点数多，搜索范围大，效率低，但能得到最优解。如果估价值大于实际值，搜索的点数少，搜索范围小，效率高，但不能保证得到最优解。
启发式搜索：启发式搜索就是在状态空间中的搜索对每一个搜索的位置进行评估，得到最好的位置，再从这个位置进行搜索直到目标。这样可以省略大量无畏的搜索路径，提到了效率。在启发式搜索中，对位置的估价是十分重要的。采用了不同的估价可以有不同的效果。

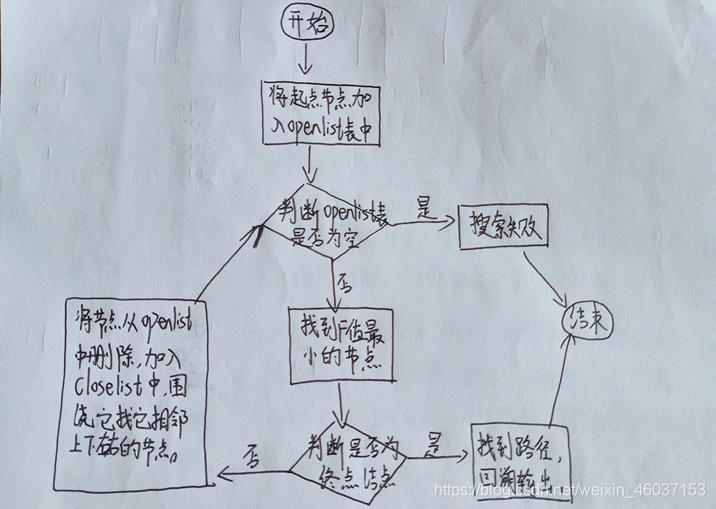
设计的求解问题的流程图的说明

A*算法寻路的求解步骤说明：
1.将起点方格（节点）加入openlist链表中，作为寻路开始的起点；
2.循环执行以下步骤，直到openlist链表为空结束或者终点（节点）加入到 openlist 中：
（1）在openlist中找到F值最小的那个节点（如果有相等的情况，就选择最先找到的那个节点）作为[ 当前节点 ]；
（2）在openlist中将第1步找到的那个F值最小的节点，从openlist中删除掉；
（3)在closelist中将第1步找到的那个F值最小的节点，加入closelist中；
(4)围绕第1步找到的那个F值最小的 [ 当前节点 ] ，找到与它相邻的 四个方向（上下左右） 上的节点，这里要判断邻居节点的有效性，看 邻居节点 是否满足以下条件：
<1>邻居节点是否越界——节点的x或者y是否在可视范围内；
<2>邻居节点是否为障碍方格（节点）——比如本程序中的 MAZE[i][j]=1 即为障碍，MAZE[i][j]=0 即为可用；
<3>邻居节点是否已经在openlist链表中或者closelist链表中；

package graph;
import java.util.ArrayList;
import java.util.List;
//A*寻路算法简单实现————>四方向（上下左右）
public class Maze_A_ManHaDun {
   
	
	//简单的迷宫模拟——利用二维数组，其中 1 表示障碍，不可通过。
	public static final int[][] MAZE= {
   
	{
   0, 1, 0, 0, 0, 0, 0},//7
	{
   0, 0, 1, 0, 0, 0, 0},
	{
   1, 0, 0, 1, 0, 0, 0},
	{
   0, 1, 0, 1, 1, 1, 1},
	{
   0, 0, 0, 0, 0, 0, 0},
	{
   0, 0, 0, 0, 0, 0, 0}