动态规划设计之最长递增子序列

题目

注意
注意「子序列」和「子串」这两个名词的区别，子串一定是连续的，而子序列不一定是连续的。下面先来设计动态规划算法解决这个问题。

思路

1. 我们先假设这个结论在 k<n 时成立，然后根据这个假设，想办法推导证明出 k=n 的时候此结论也成立。可以假设 dp[0…i-1] 都已经被算出来了，然后问自己：怎么通过这些结果算出 dp[i]？
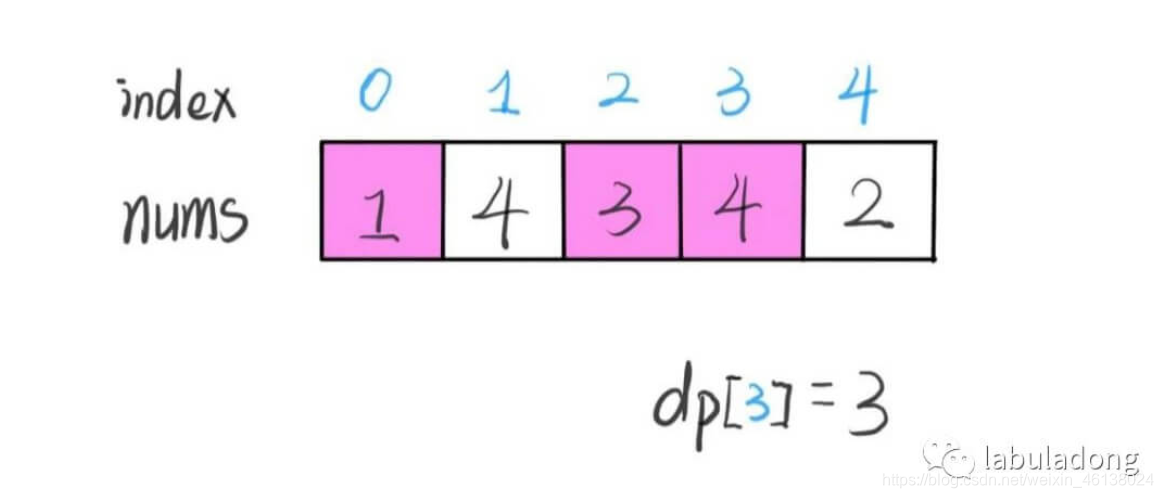
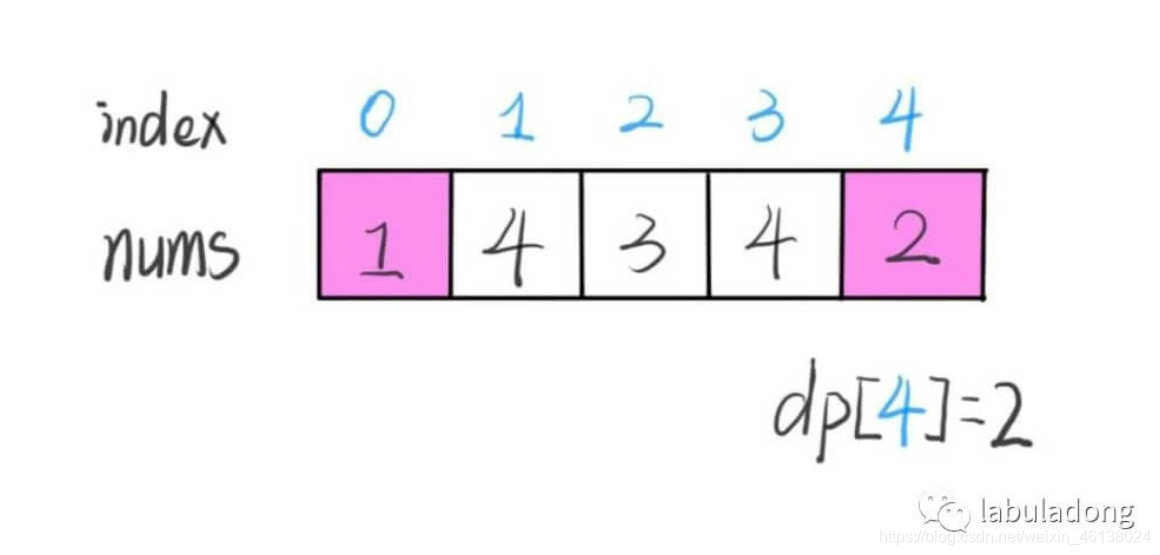
2. 定义：dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度。
   如：
   
   
3. 最终结果（子序列的最大长度）应该是 dp 数组中的最大值。
4. 假设我们已经知道了 dp[0…4] 的所有结果，我们如何通过这些已知结果推出 dp[5] 呢？
5. 既然是递增子序列，我们只要找到前面那些结尾比 3 小的子序列，然后把 3 接到最后，就可以形成一个新的递增子序列，而且这个新的子序列长度加一。

for (int i = 0; i < nums.length; i++) {
   
    for (int j = 0; j < i; j++) {
   
        if (nums[i] > nums[j]) 
            dp[i] = Math.max(dp[i], dp[j] + 1);
    }
}

完整代码

public int lengthOfLIS(int[] nums) {
   
    int[] dp = new int[nums.length];
    // base case：dp 数组全都初始化为 1
    Arrays.fill(dp, 1);
    for (int i = 0; i <