基于C语言实现内存型数据库(kv存储)
文章目录
- 源代码仓库见Github:kv-store仓库
- 配合我的讲解视频更佳:【C语言项目笔记】基于C语言实现内存型数据库(kv存储)。
- 参考视频:“零声教育”的“linux基础架构-Kv存储”。
- 其他源码:协程。
1. 项目背景
1.1 Redis介绍
本项目主要想仿照Redis的交互方式,实现一个基本的“内存型数据库”,所以首先来介绍一下Redis。随着互联网的普及,只要是上网的APP基本上都需要和相应的服务器请求数据,通常来说,这些数据被服务器保存在“磁盘”上的文件中,称之为“磁盘型数据库”。但是面对海量用户时(比如秒杀活动),磁盘IO的读写速率不够快从而导致用户体验下降,并且服务器数据库的压力也非常大。鉴于很多请求只是读取数据,这就启发我们将一些热点数据存放在内存中,以便快速响应请求、并且减轻磁盘的读写压力。
当然,上述只是一个初步的想法,后续如何清理内存数据、分布式存储等可以参考B站的科普视频,讲的非常简洁易懂:
- 【趣话Redis第一弹】我是Redis,MySQL大哥被我坑惨了!—“缓存穿透、缓存击穿、缓存雪崩”、“定时删除、惰性删除、内存淘汰”
- 【趣话Redis第二弹】Redis数据持久化AOF和RDB原理一次搞懂!—“RDB+AOF”
- 【趣话Redis第三弹】Redis的高可用是怎么实现的?哨兵是什么原理?—“主观下线、客观下线”、“哨兵选举”、“故障转移”
- 趣话Redis:Redis集群是如何工作的?—“哈希桶”、“集群工作+主从复制”
下面是一些典型的面试题:
- 为什么要使用Redis?
- 从高并发上来说:直接操作缓存能够承受的请求是远远大于直接访问数据库的,所以我们可以考虑把数据库中的部分数据转移到缓存中去。这样用户的一部分请求会直接到缓存,而不用经过数据库。
- 从高性能上来说:用户第一次访问数据库中的某些数据,因为是从硬盘上读取的,所以这个过程会比较慢。将该用户访问的数据存在缓存中,下一次再访问这些数据的时候就可以直接从缓存中获取了。操作缓存就是直接操作内存,所以速度相当快。
- 为什么要使用Redis而不是其他的,例如Java自带的map或者guava?
缓存分为本地缓存和分布式缓存,像map或者guava就是本地缓存。本地缓存最主要的特点是轻量以及快速,生命周期随着jvm的销毁而结束。在多实例的情况下,每个实例都需要各自保存一份缓存,缓存不具有一致性。redis或memcached之类的称为分布式缓存,在多实例的情况下,各实例共用一份缓存数据,缓存具有一致性。
- Redis应用场景有哪些?
- 缓存热点数据,缓解数据库的压力。
- 利用Redis原子性的自增操作,可以实现计数器的功能。比如统计用户点赞数、用户访问数等。
- 分布式锁。在分布式场景下,无法使用单机环境下的锁来对多个节点上的进程进行同步。可以使用Redis自带的SETNX命令实现分布式锁,除此之外,还可以使用官方提供的RedLock分布式锁实现。
- 简单的消息队列。可以使用Redis自身的发布/订阅模式或者List来实现简单的消息队列,实现异步操作。
- 限速器。可用于限制某个用户访问某个接口的频率,比如秒杀场景用于防止用户快速点击带来不必要的压力。
- 好友关系。利用集合的一些命令,比如交集、并集、差集等,实现共同好友、共同爱好之类的功能。
- 为什么Redis这么快?
- Redis是基于内存进行数据操作的Redis使用内存存储,没有磁盘IO上的开销,数据存在内存中,读写速度快。
- 采用IO多路复用技术。Redis使用单线程来轮询描述符,将数据库的操作都转换成了事件,不在网络I/O上浪费过多的时间。
- 高效的数据结构。Redis每种数据类型底层都做了优化,目的就是为了追求更快的速度。
1.2 项目预期及基本架构
于是我们现在就来实现这个“内存型数据库”,本项目使用C语言,默认键值对key-value都是char*类型。如上图所示,我们希望“客户端”可以和“服务端”通讯,发送相应的指令并得到相应的信息。比如“客户端”插入一个新的键值对“(name: humu)”,那么就发送“SET name humu”;“服务端”接收到这个数据包后,执行相应的操作,再返回“OK”给“客户端”。鉴于kv存储需要强查找的数据结构,我们可以使用rbtree、btree、b+tree、hash、dhash、array(数据量不多,比如http头)、skiplist、list(性能低不考虑)。最终,下表列出了我们要实现的所有数据结构及其对应的指令:
| 操作/ 数据结构 | 插入 | 查找 | 删除 | 计数 | 存在 |
|---|---|---|---|---|---|
| array | SET key value | GET key | DELETE key | COUNT | EXIST key |
| rbtree | RSET key value | RGET key | RDELETE key | RCOUNT | REXIST key |
| btree | BSET key value | BGET key | BDELETE key | BCOUNT | BEXIST key |
| hash | HSET key value | HGET key | HDELETE key | HCOUNT | HEXIST key |
| dhash | DHSET key value | DHGET key | DHDELETE key | DHCOUNT | DHEXIST key |
| skiplist | ZSET key value | ZGET key | ZDELETE key | ZCOUNT | ZEXIST key |
| 备注 | 返回OK/Fail, 表示插入键值对是否成功 | 返回对应的value | 返回OK/Fail, 删除对应的键值对 | 返回当前数据结构中 存储的键值对数量 | 返回True/False, 判断是否存在对应的键值对 |
进一步,由于网络编程中的“Hello,World!程序”就是实现一个echo,收到什么数据就原封不动的发送回去。所以我们希望在此基础上,将kv存储写成一个独立的进程,和网络收发相关代码隔离开,进而提升代码的可维护性。另外在网络协议的选择中,由于我们的键值对设置通常较短只有十几个字符(比如set key value),而http协议的协议头就有几十个字符,有效数据占比太低;udp协议只能在底层网卡确认对方收到,但没法在应用层确认,所以不可控;于是我们网络通信协议选择tcp。于是对于“服务端”,我们就可以有如下的架构设计:
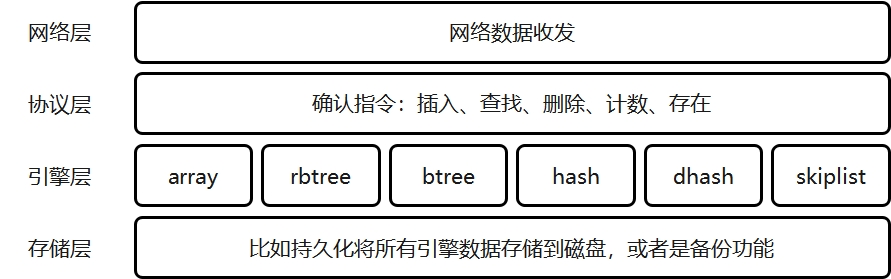
- 网络层:负责收发数据。本项目中都是“字符串”。
- 协议层:将“网络层”传输过来的字符串进行拆解,若为无效指令直接返回相应的提示信息;若为有效指令则传递给“引擎层”进行进一步的处理,根据“引擎层”的处理结果给出相应的返回信息。
- 引擎层:分为6种存储引擎,每种存储引擎都可以进行具体的增、删、查等操作,也就是实现上表给出的5种命令。
- 存储层:注意“内存型数据库”的数据在内存中,但若后续需要“持久化”也会将数据备份到磁盘中。
2. 服务端原理及代码框架
2.1 网络数据回环的实现
在使用原生的socket库函数进行网络通信时,会一直阻塞等待客户端的连接/通信请求,这个线程就做不了其他的事情,非常浪费资源。于是“reactor模式”应运而生,也被称为“基于事件驱动”,核心点在于:注册事件、监听事件、处理事件。也就是说,线程找了一个“秘书”专门负责去监听网络端口是否有“网络通信”的发生,线程就可以去做其他的事情;等到线程想处理“网络通信”的时候一起全部通知给该线程,然后这个“秘书”继续监听。显然,有这样一个“秘书”存在,可以将“网络通信”、“业务处理”分隔开,一个线程可以同时处理多个客户端的请求/通信,也就实现了“IO多路复用一个线程”。下面是常见的三种reactor模式:
- reactor单线程模型:只分配一个线程。显然若线程的“业务处理”时间过长,会导致“秘书”积压的事件过多,甚至可能会丢弃一些事件。本模型不适合计算密集型场景,只适合业务处理非常快的场景(本项目就是业务处理非常快)。
- reactor多线程模型:分配一个主线程和若干子线程。主线程只负责处理“网络通信”,“业务处理”则交给子线程处理。本模式的好处是可以充分利用多核CPU性能,但是带来了线程安全的问题。并且只有一个线程响应“网络通信”,在瞬时高并发的场景下容易成为性能瓶颈。
- 主从reactor多线程模型:在上述多线程模型的基础上,再额外开辟出新的子线程专门负责“与客户端通信”,主线程则只负责“连接请求”。
参考B站视频:【Java面试】介绍一下Reactor模式
下面使用epoll作为“秘书”,采用“reactor单线程模型”,完成网路数据回环(echo),也就是“服务端”程序框架的“网络层”:
main.c–共356行
/*
* zv开头的变量是zvnet异步网络库(epoll)。
* kv开头的变量是kv存储协议解析。
*/
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<errno.h>
#include<unistd.h>
#include<sys/socket.h>
#include<netinet/in.h>
#include<fcntl.h>
#include<sys/epoll.h>
#include"kvstore.h"
/*-------------------------------------------------------*/
/*-----------------------异步网路库-----------------------*/
/*-------------------------------------------------------*/
/*-----------------------函数声明-------------------------*/
#define max_buffer_len 1024 // 读写buffer长度
#define epoll_events_size 1024 // epoll就绪集合大小
#define connblock_size 1024 // 单个连接块存储的连接数量
#define listen_port_count 1 // 监听端口总数
// 有如下参数列表和返回之类型的函数都称为 CALLBACK
// 回调函数,方便在特定epoll事件发生时执行相应的操作
typedef int (*ZV_CALLBACK)(int fd, int events, void *arg);
// 回调函数:建立连接
int accept_cb(int fd, int event, void* arg);
// 回调函数:接收数据
int recv_cb(int clientfd, int event, void* arg);
// 回调函数:发送数据
int send_cb(int clientfd, int event, void* arg);
// 单个连接
typedef struct zv_connect_s{
// 本连接的客户端fd
int fd;
// 本连接的读写buffer
char rbuffer[max_buffer_len];
size_t rcount; // 读buffer的实际大小
char wbuffer[max_buffer_len];
size_t wcount; // 写buffer的实际大小
size_t next_len; // 下一次读数据长度(读取多个包会用到)
// 本连接的回调函数--accept()/recv()/send()
ZV_CALLBACK cb;
}zv_connect;
// 连接块的头
typedef struct zv_connblock_s{
struct zv_connect_s *block; // 指向的当前块,注意大小为 connblock_size
struct zv_connblock_s *next; // 指向的下一个连接块的头
}zv_connblock;
// 反应堆结构体
typedef struct zv_reactor_s{
int epfd; // epoll文件描述符
// struct epoll_event events[epoll_events_size]; // 就绪事件集合
struct zv_connblock_s *blockheader; // 连接块的第一个头
int blkcnt; // 现有的连接块的总数
}zv_reactor;
// reactor初始化
int init_reactor(zv_reactor *reactor);
// reator销毁
void destory_reactor(zv_reactor* reactor);
// 服务端初始化:将端口设置为listen状态
int init_sever(int port);
// 将本地的listenfd添加进epoll
int set_listener(zv_reactor *reactor, int listenfd, ZV_CALLBACK cb);
// 创建一个新的连接块(尾插法)
int zv_create_connblock(zv_reactor* reactor);
// 根据fd从连接块中找到连接所在的位置
// 逻辑:整除找到所在的连接块、取余找到在连接块的位置
zv_connect* zv_connect_idx(zv_reactor* reactor, int fd);
// 运行kv存储协议
int kv_run_while(int argc, char *argv[]);
/*-------------------------------------------------------*/
/*-----------------------函数定义-------------------------*/
// reactor初始化
int init_reactor(zv_reactor *reactor){
if(reactor == NULL) return -1;
// 初始化参数
memset(reactor, 0, sizeof(zv_reactor));
reactor->epfd = epoll_create(1);
if(reactor->epfd <= 0){
printf("init reactor->epfd error: %s\n", strerror(errno));
return -1;
}
// 为链表集合分配内存
reactor->blockheader = (zv_connblock*)calloc(1, sizeof(zv_connblock));
if(reactor->blockheader == NULL) return -1;
reactor->blockheader->next = NULL;
// 为链表集合中的第一个块分配内存
reactor->blockheader->block = (zv_connect*)calloc(connblock_size, sizeof(zv_connect));
if(reactor->blockheader->block == NULL) return -1;
reactor->blkcnt = 1;
return 0;
}
// reator销毁
void destory_reactor(zv_reactor* reactor){
if(reactor){
close(reactor->epfd); // 关闭epoll
zv_connblock* curblk = reactor->blockheader;
zv_connblock* nextblk = reactor->blockheader;
do{
curblk = nextblk;
nextblk = curblk->next;
if(curblk->block) free(curblk->block);
if(curblk) free(curblk);
}while(nextblk != NULL);
}
}
// 服务端初始化:将端口设置为listen状态
int init_sever(int port){
// 创建服务端
int sockfd = socket(AF_INET, SOCK_STREAM, 0); // io
// fcntl(sockfd, F_SETFL, O_NONBLOCK); // 非阻塞
// 设置网络地址和端口
struct sockaddr_in servaddr;
memset(&servaddr, 0, sizeof(struct sockaddr_in));
servaddr.sin_family = AF_INET; // IPv4
servaddr.sin_addr.s_addr = htonl(INADDR_ANY); // 0.0.0.0,任何地址都可以连接本服务器
servaddr.sin_port = htons(port); // 端口
// 将套接字绑定到一个具体的本地地址和端口
if(-1 == bind(sockfd, (struct sockaddr*)&servaddr, sizeof(struct sockaddr))){
printf("bind failed: %s", strerror(errno));
return -1;
}
// 将端口设置为listen(并不会阻塞程序执行)
listen(sockfd, 10); // 等待连接队列的最大长度为10
printf("listen port: %d, sockfd: %d\n", port, sockfd);
return sockfd;
}
// 将本地的listenfd添加进epoll
int set_listener(zv_reactor *reactor, int listenfd, ZV_CALLBACK cb){
if(!reactor || !reactor->blockheader) return -1;
// 将服务端放进连接块
reactor->blockheader->block[listenfd].fd = listenfd;
reactor->blockheader->block[listenfd].cb = cb; // listenfd的回调函数应该是accept()
// 将服务端添加进epoll事件
struct epoll_event ev;
ev.data.fd = listenfd;
ev.events = EPOLLIN;
epoll_ctl(reactor->epfd, EPOLL_CTL_ADD, listenfd, &ev);
return 0;
}
// 创建一个新的连接块(尾插法)
int zv_create_connblock(zv_reactor* reactor){
if(!reactor) return -1;
// 初始化新的连接块
zv_connblock* newblk = (zv_connblock*)calloc(1, sizeof(zv_connblock));
if(newblk == NULL) return -1;
newblk->block = (zv_connect*)calloc(connblock_size, sizeof(zv_connect));
if(newblk->block == NULL) return -1;
newblk->next = NULL;
// 找到最后一个连接块
zv_connblock* endblk = reactor->blockheader;
while(endblk->next != NULL){
endblk = endblk->next;
}
// 添加上新的连接块
endblk->next = newblk;
reactor->blkcnt++;
return 0;
}
// 根据fd从连接块中找到连接所在的位置
// 逻辑:整除找到所在的连接块、取余找到在连接块的位置
zv_connect* zv_connect_idx(zv_reactor* reactor, int fd){
if(!reactor) return NULL;
// 计算fd应该在的连接块
int blkidx = fd / connblock_size;
while(blkidx >= reactor->blkcnt){
zv_create_connblock(reactor);
// printf("create a new connblk!\n");
}
// 找到这个连接块
zv_connblock* blk = reactor->blockheader;
int i = 0;
while(++i < blkidx){
blk = blk->next;
}
return &blk->block[fd % connblock_size];
}
// 回调函数:建立连接
// fd:服务端监听端口listenfd
// event:没用到,但是回调函数的常用格式
// arg:应该是reactor*
int accept_cb(int fd, int event, void* arg){
// 与客户端建立连接
struct sockaddr_in clientaddr; // 连接到本服务器的客户端信息
socklen_t len_sockaddr = sizeof(clientaddr);
int clientfd = accept(fd, (struct sockaddr*)&clientaddr, &len_sockaddr);
if(clientfd < 0){
printf("accept() error: %s\n", strerror(errno));
return -1;
}
// 将连接添加进连接块
zv_reactor* reactor = (zv_reactor*)arg;
zv_connect* conn = zv_connect_idx(reactor, clientfd);
conn->fd = clientfd;
conn->cb = recv_cb;
conn->next_len = max_buffer_len;
conn->rcount = 0;
conn->wcount = 0;
// 将客户端添加进epoll事件
struct epoll_event ev;
ev.data.fd = clientfd;
ev.events = EPOLLIN; // 默认水平触发(有数据就触发)
epoll_ctl(reactor->epfd, EPOLL_CTL_ADD, clientfd, &ev);
printf("connect success! sockfd:%d, clientfd:%d\n", fd, clientfd);
}
// 回调函数:接收数据
int recv_cb(int clientfd, int event, void* arg){
zv_reactor* reactor = (zv_reactor*)arg;
zv_connect* conn = zv_connect_idx(reactor, clientfd);
int recv_len = recv(clientfd, conn->rbuffer+conn->rcount, conn->next_len, 0); // 由于当前fd可读所以没有阻塞
if(recv_len < 0){
printf("recv() error: %s\n", strerror(errno));
close(clientfd);
// return -1;
exit(0);
}else if(recv_len == 0){
// 重置对应的连接块
conn->fd = -1;
conn->rcount = 0;
conn->wcount = 0;
// 从epoll监听事件中移除
epoll_ctl(reactor->epfd, EPOLL_CTL_DEL, clientfd, NULL);
// 关闭连接
close(clientfd);
printf("close clientfd:%d\n", clientfd);
}else if(recv_len > 0){
conn->rcount += recv_len;
// conn->next_len = *(short*)conn->rbuffer; // 从tcp协议头中获取数据长度,假设前两位是长度
// 处理接收到的字符串,并将需要发回的信息存储在缓冲区中
printf("recv clientfd:%d, len:%d, mess: %s\n", clientfd, recv_len, conn->rbuffer);
// conn->rcount = kv_protocal(conn->rbuffer, max_buffer_len);
// 将kv存储的回复消息(rbuffer)拷贝给wbuffer
// printf("msg:%s len:%ld\n", msg, strlen(msg));
memset(conn->wbuffer, '\0', max_buffer_len);
memcpy(conn->wbuffer, conn->rbuffer, conn->rcount);
conn->wcount = conn->rcount;
memset(conn->rbuffer, 0, max_buffer_len);
conn->rcount = 0;
// 将本连接更改为epoll写事件
conn->cb = send_cb;
struct epoll_event ev;
ev.data.fd = clientfd;
ev.events = EPOLLOUT;
epoll_ctl(reactor->epfd, EPOLL_CTL_MOD, clientfd, &ev);
}
return 0;
}
// 回调函数:发送数据
int send_cb(int clientfd, int event, void* arg){
zv_reactor* reactor = (zv_reactor*)arg;
zv_connect* conn = zv_connect_idx(reactor, clientfd);
int send_len = send(clientfd, conn->wbuffer, conn->wcount, 0);
if(send_len < 0){
printf("send() error: %s\n", strerror(errno));
close(clientfd);
return -1;
}
memset(conn->wbuffer, 0, conn->next_len);
conn->wcount -= send_len;
// 发送完成后将本连接再次更改为读事件
conn->cb = recv_cb;
struct epoll_event ev;
ev.data.fd = clientfd;
ev.events = EPOLLIN;
epoll_ctl(reactor->epfd, EPOLL_CTL_MOD, clientfd, &ev);
return 0;
}
// 运行kv存储协议
int kv_run_while(int argc, char *argv[]){
// 创建管理连接的反应堆
// zv_reactor reactor;
zv_reactor *reactor = (zv_reactor*)malloc(sizeof(zv_reactor));
init_reactor(reactor);
// 服务端初始化
int start_port = atoi(argv[1]);
for(int i=0; i<listen_port_count; i++){
int sockfd = init_sever(start_port+i);
set_listener(reactor, sockfd, accept_cb); // 将sockfd添加进epoll
}
printf("init finish, listening connet...\n");
// 开始监听事件
struct epoll_event events[epoll_events_size] = {0}; // 就绪事件集合
while(1){
// 等待事件发生
int nready = epoll_wait(reactor->epfd, events, epoll_events_size, -1); // -1等待/0不等待/正整数则为等待时长
if(nready == -1){
printf("epoll_wait error: %s\n", strerror(errno));
break;
}else if(nready == 0){
continue;
}else if(nready > 0){
// printf("process %d epoll events...\n", nready);
// 处理所有的就绪事件
int i = 0;
for(i=0; i<nready; i++){
int connfd = events[i].data.fd;
zv_connect* conn = zv_connect_idx(reactor, connfd);
// 回调函数和下面的的逻辑实现了数据回环
if(EPOLLIN & events[i].events){
conn->cb(connfd, events[i].events, reactor);
}
if(EPOLLOUT & events[i].events){
conn->cb(connfd, events[i].events, reactor);
}
}
}
}
destory_reactor(reactor);
return 0;
}
int main(int argc, char *argv[]){
if(argc != 2){
printf("please enter port! e.x. 9999.\n");
return -1;
}
// 初始化存储引擎
// kv_engine_init();
// 运行kv存储
kv_run_while(argc, argv);
// 销毁存储引擎
// kv_engine_desy();
return 0;
}
/*-------------------------------------------------------*/
注:只有251行、346行、352行是后续和kv存储有关的接口函数。可以发现“网络层”和“协议层”被很好的隔离开来。
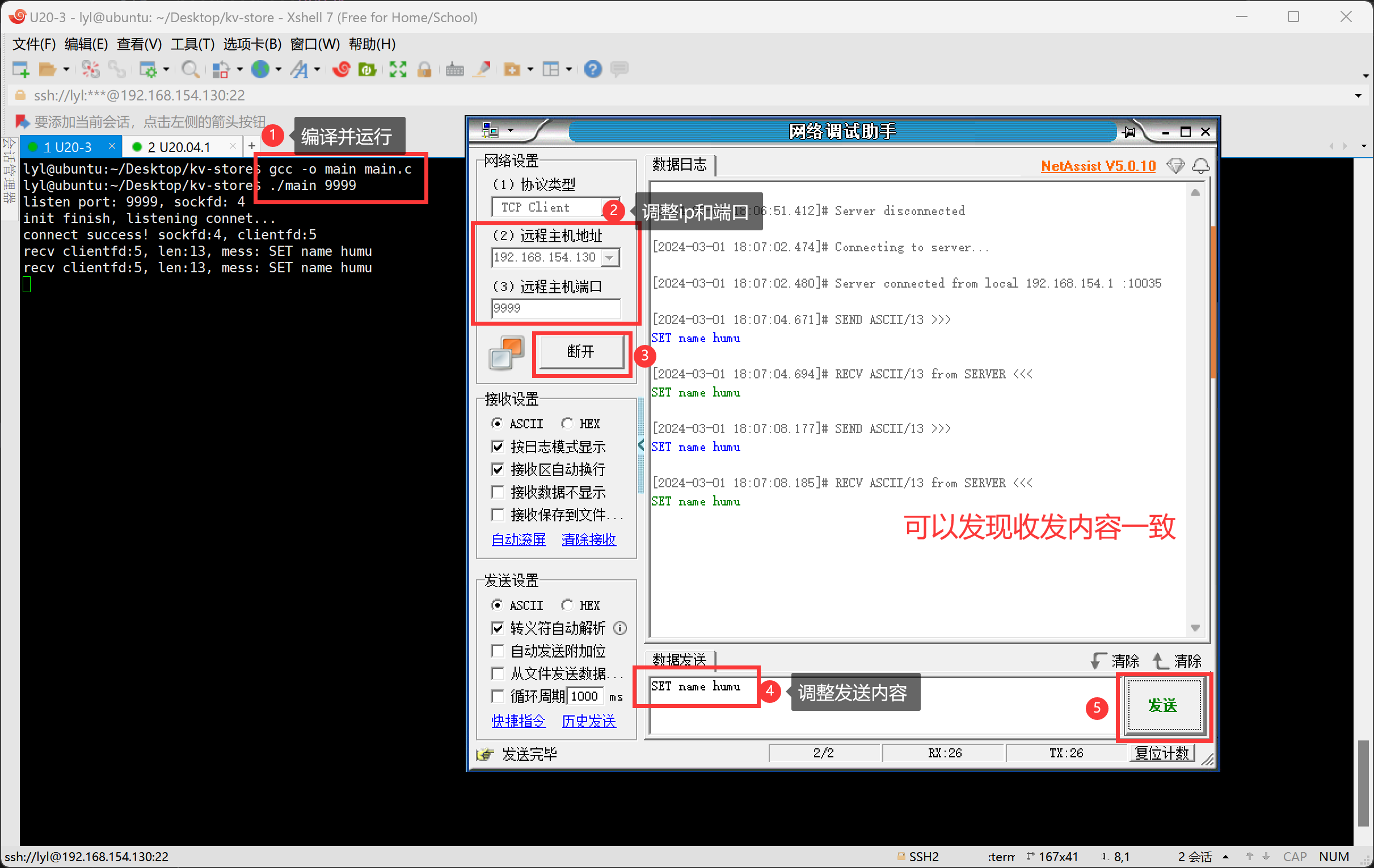
可以看到上述实现了网络数据回环的功能。并且进一步来说,假如客户端使用浏览器(http协议)对该端口进行访问,那么对接收到的数据包进行http协议拆包,根据其请求的内容返回相应的信息(如html文件),那么就是我们所熟知的“web服务器”了。为什么是“烂大街”啊,一代比一代卷是吧😭。
2.2 array的实现
现在使用“数组”来存储“键值对节点”。首先我们可以想到的是,直接定义一个长度足够大的数组(如1024),然后每次“插入”就直接找第一个空节点,“查找”和“删除”都是遍历所有节点。但是数组长度固定是一件很危险的事情,所以我们可以借鉴“内存池”的思想,来自动进行扩容和缩容。
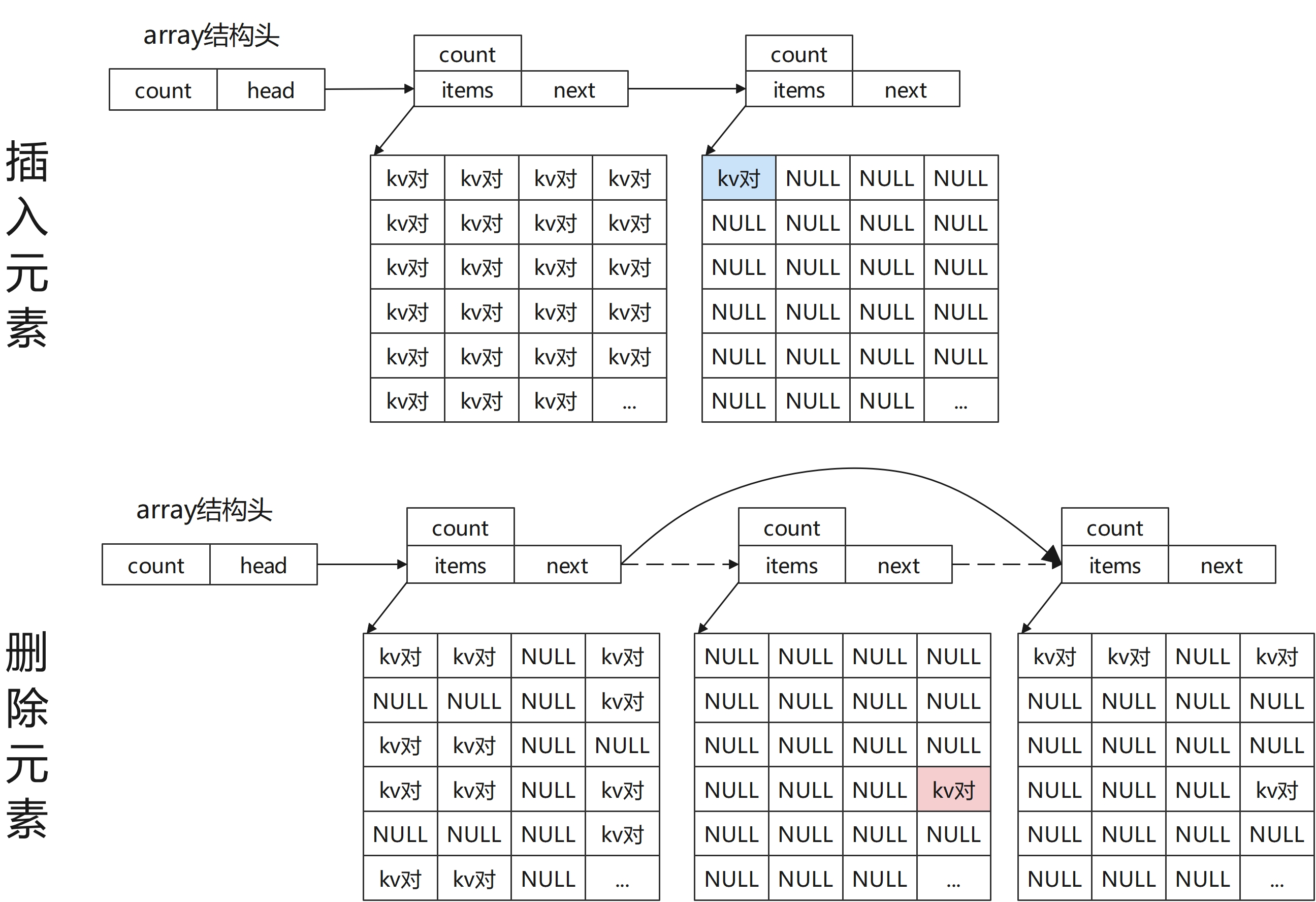
如上图所示,首先申请一个固定大小的“数组”存储元素,当在某次“插入”元素发现没有空节点时,可以直接再申请一块“数组”,并将当前数组指向这个新数组;同理,当我们“删除”一个元素时,若发现删除后当前数组块为空,可以直接free掉这块内存,然后将其前后的内存块连起来。注意到,为了能帮助我们快速判断某个数组块是否为空,还需要在其结构体中定义当前数组块的有效元素数量count。
array结构的增/删/查操作还是比较简单的,可以直接参考项目源码中的“array.h”、“array.c”。
2.3 rbtree的实现
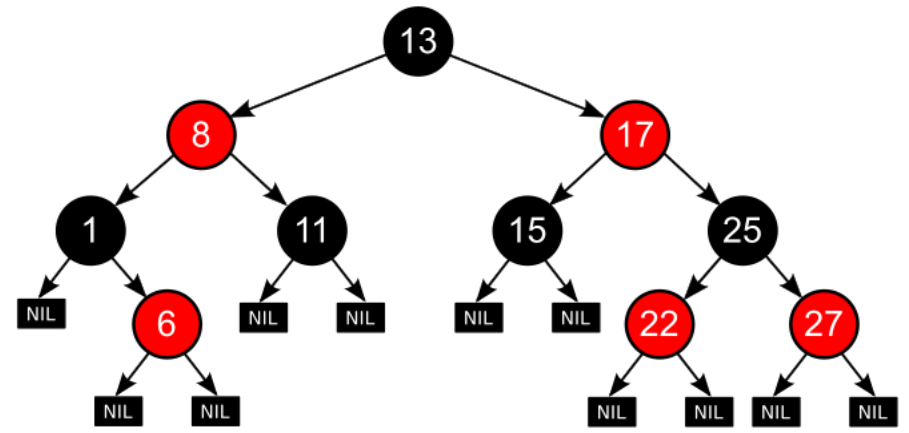
红黑树是一种“自平衡的二叉搜索树”,可谓是耳熟能详,其增删查改的操作都已经非常成熟。通俗来说,红黑树本质上是一个二叉树,而一个满二叉树的查找性能近似于 O ( log N ) O(\log N) O(logN),于是我们便希望每次插入/删除元素时,红黑树都能把自己调整成近乎于满二叉树的状态。具体来说,就是在普通二叉树的基础上,只需要为每个节点额外添加一个“颜色信息”,再额外规定一些必须满足的性质,就可以保证红黑树始终平衡。下面是红黑树的性质–来源中文维基百科“红黑树”:
- 每个节点是红的或者黑的。
- 根结点是黑的。
- 所有叶子节点都是黑的(叶子节点是nil节点)。
- 红色节点的子节点必须是黑色。(或者说红色节点不相邻)
- 从任一节点到其每个叶子节点的所有简单路径,都包含相同数目的黑色节点。
“nil节点”:是一个黑色的空节点,作为红黑树的叶子节点。
性质口诀:左根右,根叶黑,不红红,黑路同
注:零声教育提供了能显示红黑树生成步骤的本地HTML文件–“红黑树生成步骤.html(39KB)”。
红黑树的查找操作只需要从根节点不断比较即可,而红黑树的插入/删除操作则有点说法。下面是我按照编程逻辑进行简化的插入/删除原理。具体来说,就是每次插入/删除后都需要进行调整,调整的逻辑如下:
红黑树插入:刚插入的位置一定是叶子节点,颜色为红,然后按照如下方式调整。
// 父节点是黑色:无需操作。 while(父节点是红色){ if(叔节点为红色){ 变色:祖父变红/父变黑/叔变黑、祖父节点成新的当前节点。 进入下一次循环。 }else(叔节点是黑色,注意叶子节点也是黑色){ 判断“祖父节点->父节点->当前节点”的左右走向: LL:祖父变红/父变黑、祖父右旋。最后的当前节点应该是原来的当前节点。 LR:祖父变红/父变红/当前变黑、父左旋/祖父右旋。最后的当前节点应该是原来的祖父节点/父节点。 RL:祖父变红/父变红/当前变黑、父右旋/祖父左旋。最后的当前节点应该是原来的祖父节点/父节点。 RR:祖父变红/父变黑、祖父左旋。最后的当前节点应该是原来的当前节点。 然后进入下一次循环。 } }红黑树删除:要删除的位置一定是 没有/只有一个 孩子。也就是说,如果要删除的元素有两个孩子,那就和其后继节点交换键值对,然后实际删除这个后继节点。实际删除的节点
del_r为黑色,则将“孩子节点”(没有孩子就是左侧的叶子节点)作为“当前节点”按照如下方式调整。while(当前节点是黑色 && 不是根节点){ if(兄弟节点为红色){ if(当前节点是左孩子)父变红/兄弟变黑、父左旋,当前节点下一循环。 else(当前节点是右孩子)父变红/兄弟变黑、父右旋,当前节点下一循环。 } else(兄弟节点为黑色){ if(兄弟节点没有红色子节点){ if(父为黑)父变黑/兄弟变红,父节点成新的当前节点进入下一循环。 else(父为红)父变黑/兄弟变红,结束循环(当前节点指向根节点)。 }else(兄弟节点有红色子节点){ 判断“父节点->兄弟节点->兄弟的红色子节点(两个子节点都是红色则默认是左)”的走向: LL:红子变黑/兄弟变父色、父右旋、父变黑,结束循环。 LR:红子变父色、兄弟左旋/父右旋、父变黑,结束循环。 RR:红子变黑/兄弟变父色、父左旋、父变黑,结束循环。 RL:红子变父色、兄弟右旋/父左旋、父变黑,结束循环。 “结束循环”等价于当前节点指向根节点。 } } } 注意出了循环别忘了将根节点调整成黑色。
根据上述原理,我使用C语言实现了红黑树完整的增删查操作,并增加了检验有效性、打印红黑树图的代码,以及测试代码。值得注意的是,为了加快开发速度,下面的代码预设“键值对”的类型为int key、void* value,也就是只关心int型的key、不关心value,后续将红黑树添加进“kv存储协议”中时会进一步修改:
rbtree_int.c-共905行
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<stdbool.h>
// 编译指令:gcc -o main rbtree_int.c
// 本代码实现红黑树,存储int型key,未指定value。
#define RBTREE_DEBUG 1 // 是否运行测试代码
typedef int KEY_TYPE; // 节点的key类型
#define RED 1
#define BLACK 0
// 定义红黑树单独节点
typedef struct _rbtree_node {
KEY_TYPE key; // 键
void *value; // 值,可以指向任何类型
struct _rbtree_node *left;
struct _rbtree_node *right;
struct _rbtree_node *parent;
unsigned char color; // 不同编译器的无符号性质符号不同,这里加上unsigned减少意外。
/* 对于32位系统,上述只有color是1个字节,其余都是4个字节,所以color放在最后可以节省内存。 */
} rbtree_node;
// 定义整个红黑树
typedef struct _rbtree{
struct _rbtree_node *root_node; // 根节点
struct _rbtree_node *nil_node; // 空节点,也就是叶子节点、根节点的父节点
} rbtree;
// 存储打印红黑树所需的参数
typedef struct _disp_parameters{
// 打印缓冲区
char **disp_buffer;
// 打印缓冲区的深度,宽度,当前打印的列数
int disp_depth;
int disp_width;
int disp_column;
// 树的深度
int max_depth;
// 最大的数字位宽
int max_num_width;
// 单个节点的显示宽度
int node_width;
}disp_parameters;
/*----初始化及释放内存----*/
// 红黑树初始化,注意调用完后释放内存rbtree_free
rbtree *rbtree_malloc(void);
// 红黑树释放内存
void rbtree_free(rbtree *T);
/*----插入操作----*/
// 红黑树插入
void rbtree_insert(rbtree *T, KEY_TYPE key, void *value);
// 调整插入新节点后的红黑树,使得红色节点不相邻(平衡性)
void rbtree_insert_fixup(rbtree *T, rbtree_node *cur);
/*----删除操作----*/
// 红黑树删除
void rbtree_delete(rbtree *T, rbtree_node *del);
// 调整删除某节点后的红黑树,使得红色节点不相邻(平衡性)
void rbtree_delete_fixup(rbtree *T, rbtree_node *cur);
/*----查找操作----*/
// 红黑树查找
rbtree_node* rbtree_search(rbtree *T, KEY_TYPE key);
/*----打印信息----*/
// 中序遍历整个红黑树,依次打印节点信息
void rbtree_traversal(rbtree *T);
// 以图的形式展示红黑树
void rbtree_display(rbtree *T);
// 先序遍历,打印红黑树信息到字符数组指针
void set_display_buffer(rbtree *T, rbtree_node *cur, disp_parameters *p);
/*----检查有效性----*/
// 检查当前红黑树的有效性:根节点黑色、红色不相邻、所有路径黑高相同
bool rbtree_check_effective(rbtree *T);
/*----其他函数----*/
// 在给定节点作为根节点的子树中,找出key最小的节点
rbtree_node* rbtree_min(rbtree *T, rbtree_node *cur);
// 在给定节点作为根节点的子树中,找出key最大的节点
rbtree_node* rbtree_max(rbtree *T, rbtree_node *cur);
// 找出当前节点的前驱节点
rbtree_node* rbtree_precursor_node(rbtree *T, rbtree_node *cur);
// 找出当前节点的后继节点
rbtree_node* rbtree_successor_node(rbtree *T, rbtree_node *cur);
// 红黑树节点左旋,无需修改颜色
void rbtree_left_rotate(rbtree *T, rbtree_node *x);
// 红黑树节点右旋,无需修改颜色
void rbtree_right_rotate(rbtree *T, rbtree_node *y);
// 计算红黑树的深度
int rbtree_depth(rbtree *T);
// 递归计算红黑树的深度(不包括叶子节点)
int rbtree_depth_recursion(rbtree *T, rbtree_node *cur);
/*-----------------------------下面为函数定义-------------------------------*/
// 红黑树初始化,注意调用完后释放内存rbtree_free()
rbtree *rbtree_malloc(void){
rbtree *T = (rbtree*)malloc(sizeof(rbtree));
if(T == NULL){
printf("rbtree malloc failed!");
}else{
T->nil_node = (rbtree_node*)malloc(sizeof(rbtree_node));
T->nil_node->color = BLACK;
T->nil_node->left = T->nil_node;
T->nil_node->right = T->nil_node;
T->nil_node->parent = T->nil_node;
T->root_node = T->nil_node;
}
return T;
}
// 红黑树释放内存
void rbtree_free(rbtree *T){
free(T->nil_node);
free(T);
}
// 在给定节点作为根节点的子树中,找出key最小的节点
rbtree_node* rbtree_min(rbtree *T, rbtree_node *cur){
while(cur->left != T->nil_node){
cur = cur->left;
}
return cur;
}
// 在给定节点作为根节点的子树中,找出key最大的节点
rbtree_node* rbtree_max(rbtree *T, rbtree_node *cur){
while(cur->right != T->nil_node){
cur = cur->right;
}
return cur;
}
// 找出当前节点的前驱节点
rbtree_node* rbtree_precursor_node(rbtree *T, rbtree_node *cur){
// 若当前节点有左孩子,那就直接向下找
if(cur->left != T->nil_node){
return rbtree_max(T, cur->left);
}
// 若当前节点没有左孩子,那就向上找
rbtree_node *parent = cur->parent;
while((parent != T->nil_node) && (cur == parent->left)){
cur = parent;
parent = cur->parent;
}
return parent;
// 若返回值为空节点,则说明当前节点就是第一个节点
}
// 找出当前节点的后继节点
rbtree_node* rbtree_successor_node(rbtree *T, rbtree_node *cur){
// 若当前节点有右孩子,那就直接向下找
if(cur->right != T->nil_node){
return rbtree_min(T, cur->right);
}
// 若当前节点没有右孩子,那就向上找
rbtree_node *parent = cur->parent;
while((parent != T->nil_node) && (cur == parent->right)){
cur = parent;
parent = cur->parent;
}
return parent;
// 若返回值为空节点,则说明当前节点就是最后一个节点
}
// 红黑树节点左旋,无需修改颜色
void rbtree_left_rotate(rbtree *T, rbtree_node *x){
// 传入rbtree*是为了判断节点node的左右子树是否为叶子节点、父节点是否为根节点。
rbtree_node *y = x->right;
// 注意红黑树中所有路径都是双向的,两边的指针都要改!
// 另外,按照如下的修改顺序,无需存储额外的节点。
x->right = y->left;
if(y->left != T->nil_node){
y->left->parent = x;
}
y->parent = x->parent;
if(x->parent == T->nil_node){ // x为根节点
T->root_node = y;
}else if(x->parent->left == x){
x->parent->left = y;
}else{
x->parent->right = y;
}
y->left = x;
x->parent = y;
}
// 红黑树节点右旋,无需修改颜色
void rbtree_right_rotate(rbtree *T, rbtree_node *y){
rbtree_node *x = y->left;
y->left = x->right;
if(x->right != T->nil_node){
x->right->parent = y;
}
x->parent = y->parent;
if(y->parent == T->nil_node){
T->root_node = x;
}else if(y->parent->left == y){
y->parent->left = x;
}else{
y->parent->right = x;
}
x->right = y;
y->parent = x;
}
// 调整插入新节点后的红黑树,使得红色节点不相邻(平衡性)
void rbtree_insert_fixup(rbtree *T, rbtree_node *cur){
// 父节点是黑色,无需调整。
// 父节点是红色,则有如下八种情况。
while(cur->parent->color == RED){
// 获取叔节点
rbtree_node *uncle;
if(cur->parent->parent->left == cur->parent){
uncle = cur->parent->parent->right;
}else{
uncle = cur->parent->parent->left;
}
// 若叔节点为红,只需更新颜色(隐含了四种情况)
// 循环主要在这里起作用
if(uncle->color == RED){
// 叔节点为红色:祖父变红/父变黑/叔变黑、祖父节点成新的当前节点。
if(uncle->color == RED){
cur->parent->parent->color = RED;
cur->parent->color = BLACK;
uncle->color = BLACK;
cur = cur->parent->parent;
}
}
// 若叔节点为黑,需要变色+旋转(当前节点相当于祖父节点位置包括四种情况:LL/RR/LR/RL)
// 下面对四种情况进行判断:都是只执行一次
else{
if(cur->parent->parent->left == cur->parent){
// LL:祖父变红/父变黑、祖父右旋。最后的当前节点应该是原来的当前节点。
if(cur->parent->left == cur){
cur->parent->parent->color = RED;
cur->parent->color = BLACK;
rbtree_right_rotate(T, cur->parent->parent);
}
// LR:祖父变红/父变红/当前变黑、父左旋、祖父右旋。最后的当前节点应该是原来的祖父节点。
else{
cur->parent->parent->color = RED;
cur->parent->color = RED;
cur->color = BLACK;
cur = cur->parent;
rbtree_left_rotate(T, cur);
rbtree_right_rotate(T, cur->parent->parent);
}
}
else{
// RL:祖父变红/父变红/当前变黑、父右旋、祖父左旋。最后的当前节点应该是原来的祖父节点。
if(cur->parent->left == cur){
cur->parent->parent->color = RED;
cur->parent->color = RED;
cur->color = BLACK;
cur = cur->parent;
rbtree_right_rotate(T, cur);
rbtree_left_rotate(T, cur->parent->parent);
}
// RR:祖父变红/父变黑、祖父左旋。最后的当前节点应该是原来的当前节点。
else{
cur->parent->parent->color = RED;
cur->parent->color = BLACK;
rbtree_left_rotate(T, cur->parent->parent);
}
}
}
}
// 将根节点变为黑色
T->root_node->color = BLACK;
}
// 插入
// void rbtree_insert(rbtree *T, rbtree_node *new){
void rbtree_insert(rbtree *T, KEY_TYPE key, void *value){
// 创建新节点
rbtree_node *new = (rbtree_node*)malloc(sizeof(rbtree_node));
new->key = key;
new->value = value;
// 寻找插入位置(红黑树中序遍历升序)
rbtree_node *cur = T->root_node;
rbtree_node *next = T->root_node;
// 刚插入的位置一定是叶子节点
while(next != T->nil_node){
cur = next;
if(new->key > cur->key){
next = cur->right;
}else if(new->key < cur->key){
next = cur->left;
}else if(new->key == cur->key){
// 红黑树本身没有明确如何处理key相同节点,所以取决于业务。
// 场景1:统计不同课程的人数,相同就+1。
// 场景2:时间戳,若相同则稍微加一点
// 其他场景:覆盖、丢弃...
printf("Already have the same key=%d!\n", new->key);
free(new);
return;
}
}
if(cur == T->nil_node){
// 若红黑树本身没有节点
T->root_node = new;
}else if(new->key > cur->key){
cur->right = new;
}else{
cur->left = new;
}
new->parent = cur;
new->left = T->nil_node;
new->right = T->nil_node;
new->color = RED;
// 调整红黑树,使得红色节点不相邻
rbtree_insert_fixup(T, new);
}
// 调整删除某节点后的红黑树,使得红色节点不相邻(平衡性)
void rbtree_delete_fixup(rbtree *T, rbtree_node *cur){
// child是黑色、child不是根节点才会进入循环
while((cur->color == BLACK) && (cur != T->root_node)){
// 获取兄弟节点
rbtree_node *brother = T->nil_node;
if(cur->parent->left == cur){
brother = cur->parent->right;
}else{
brother = cur->parent->left;
}
// 兄弟节点为红色:父变红/兄弟变黑、父单旋、当前节点下一循环
if(brother->color == RED){
cur->parent->color = RED;
brother->color = BLACK;
if(cur->parent->left == cur){
rbtree_left_rotate(T, cur->parent);
}else{
rbtree_right_rotate(T, cur->parent);
}
}
// 兄弟节点为黑色
else{
// 兄弟节点没有红色子节点:父变黑/兄弟变红、看情况是否结束循环
if((brother->left->color == BLACK) && (brother->right->color == BLACK)){
// 若父原先为黑,父节点成新的当前节点进入下一循环;否则结束循环。
if(brother->parent->color == BLACK){
cur = cur->parent;
}else{
cur = T->root_node;
}
brother->parent->color = BLACK;
brother->color = RED;
}
// 兄弟节点有红色子节点:LL/LR/RR/RL
else if(brother->parent->left == brother){
// LL:红子变黑/兄弟变父色/父变黑、父右旋,结束循环
if(brother->left->color == RED){
brother->left->color = BLACK;
brother->color = brother->parent->color;
brother->parent->color = BLACK;
rbtree_right_rotate(T, brother->parent);
cur = T->root_node;
}
// LR:红子变父色/父变黑、兄弟左旋/父右旋,结束循环
else{
brother->right->color = brother->parent->color;
cur->parent->color = BLACK;
rbtree_left_rotate(T, brother);
rbtree_right_rotate(T, cur->parent);
cur = T->root_node;
}
}else{
// RR:红子变黑/兄弟变父色/父变黑、父左旋,结束循环
if(brother->right->color == RED){
brother->right->color = BLACK;
brother->color = brother->parent->color;
brother->parent->color = BLACK;
rbtree_left_rotate(T, brother->parent);
cur = T->root_node;
}
// RL:红子变父色/父变黑、兄弟右旋/父左旋,结束循环
else{
brother->left->color = brother->parent->color;
brother->parent->color = BLACK;
rbtree_right_rotate(T, brother);
rbtree_left_rotate(T, cur->parent);
cur = T->root_node;
}
}
}
}
// 下面这行处理情况2/3
cur->color = BLACK;
}
// 红黑树删除
void rbtree_delete(rbtree *T, rbtree_node *del){
if(del != T->nil_node){
/* 红黑树删除逻辑:
1. 标准的BST删除操作(本函数):最红都会转换成删除只有一个子节点或者没有子节点的节点。
2. 若删除节点为黑色,则进行调整(rebtre_delete_fixup)。
*/
rbtree_node *del_r = T->nil_node; // 实际删除的节点
rbtree_node *del_r_child = T->nil_node; // 实际删除节点的子节点
// 找出实际删除的节点
// 注:实际删除的节点最多只有一个子节点,或者没有子节点(必然在最后两层中,不包括叶子节点那一层)
if((del->left == T->nil_node) || (del->right == T->nil_node)){
// 如果要删除的节点本身就只有一个孩子或者没有孩子,那实际删除的节点就是该节点
del_r = del;
}else{
// 如果要删除的节点有两个孩子,那就使用其后继节点(必然最多只有一个孩子)
del_r = rbtree_successor_node(T, del);
}
// 看看删除节点的孩子是谁,没有孩子就是空节点
if(del_r->left != T->nil_node){
del_r_child = del_r->left;
}else{
del_r_child = del_r->right;
}
// 将实际要删除的节点删除
del_r_child->parent = del_r->parent; // 若child为空节点,最后再把父节点指向空节点
if(del_r->parent == T->nil_node){
T->root_node = del_r_child;
}else if(del_r->parent->left == del_r){
del_r->parent->left = del_r_child;
}else{
del_r->parent->right = del_r_child;
}
// 替换替换键值对
if(del != del_r){
del->key = del_r->key;
del->value = del_r->value;
}
// 最后看是否需要调整
if(del_r->color == BLACK){
rbtree_delete_fixup(T, del_r_child);
}
// 调整空节点的父节点
if(del_r_child == T->nil_node){
del_r_child->parent = T->nil_node;
}
free(del_r);
}
}
// 查找
rbtree_node* rbtree_search(rbtree *T, KEY_TYPE key){
rbtree_node *cur = T->root_node;
while(cur != T->nil_node){
if(cur->key > key){
cur = cur->left;
}else if(cur->key < key){
cur = cur->right;
}else{
return cur;
}
}
printf("There is NO key=%d in rbtree!\n", key);
return T->nil_node;
}
// 中序遍历给定结点为根节点的子树(递归)
void rbtree_traversal_node(rbtree *T, rbtree_node *cur){
if(cur != T->nil_node){
rbtree_traversal_node(T, cur->left);
if(cur->color == RED){
printf("Key:%d\tColor:Red\n", cur->key);
}else{
printf("Key:%d\tColor:Black\n", cur->key);
}
rbtree_traversal_node(T, cur->right);
}
}
// 中序遍历整个红黑树
void rbtree_traversal(rbtree *T){
rbtree_traversal_node(T, T->root_node);
}
// 递归计算红黑树的深度(不包括叶子节点)
int rbtree_depth_recursion(rbtree *T, rbtree_node *cur){
if(cur == T->nil_node){
return 0;
}else{
int left = rbtree_depth_recursion(T, cur->left);
int right = rbtree_depth_recursion(T, cur->right);
return ((left > right) ? left : right) + 1;
}
}
// 计算红黑树的深度
int rbtree_depth(rbtree *T){
return rbtree_depth_recursion(T, T->root_node);
}
// 获取输入数字的十进制显示宽度
int decimal_width(int num_in){
int width = 0;
while (num_in != 0){
num_in = num_in / 10;
width++;
}
return width;
}
// 先序遍历,打印红黑树信息到字符数组指针
void set_display_buffer(rbtree *T, rbtree_node *cur, disp_parameters *p){
if(cur != T->nil_node){
// 输出当前节点
p->disp_depth++;
// 输出数字到缓冲区
char num_char[20];
char formatString[20];
int cur_num_width = decimal_width(cur->key);
int num_space = (p->node_width - 2 - cur_num_width) >> 1; // 数字后面需要补充的空格数量
strncpy(formatString, "|%*d", sizeof(formatString));
int i = 0;
for(i=0; i<num_space; i++){
strncat(formatString, " ", 2);
}
strncat(formatString, "|", 2);
snprintf(num_char, sizeof(num_char), formatString, (p->node_width-2-num_space), cur->key);
i = 0;
while(num_char[i] != '\0'){
p->disp_buffer[(p->disp_depth-1)*3][p->disp_column+i] = num_char[i];
i++;
}
// 输出颜色到缓冲区
char color_char[20];
if(cur->color == RED){
num_space = (p->node_width-2-3)>>1;
strncpy(color_char, "|", 2);
for(i=0; i<(p->node_width-2-3-num_space); i++){
strncat(color_char, " ", 2);
}
strncat(color_char, "RED", 4);
for(i=0; i<num_space; i++){
strncat(color_char, " ", 2);
}
strncat(color_char, "|", 2);
}else{
num_space = (p->node_width-2-5)>>1;
strncpy(color_char, "|", 2);
for(i=0; i<(p->node_width-2-5-num_space); i++){
strncat(color_char, " ", 2);
}
strncat(color_char, "BLACK", 6);
for(i=0; i<num_space; i++){
strncat(color_char, " ", 2);
}
strncat(color_char, "|", 2);
}
// strcpy(color_char, (cur->color == RED) ? "| RED |" : "|BLACK|");
i = 0;
while(color_char[i] != '\0'){
p->disp_buffer[(p->disp_depth-1)*3+1][p->disp_column+i] = color_char[i];
i++;
}
// 输出连接符到缓冲区
if(p->disp_depth>1){
char connector_char[10];
strcpy(connector_char, (cur->parent->left == cur) ? "/" : "\\");
p->disp_buffer[(p->disp_depth-1)*3-1][p->disp_column+(p->node_width>>1)] = connector_char[0];
}
// 下一层需要前进/后退的字符数
int steps = 0;
if(p->disp_depth+1 == p->max_depth){
steps = (p->node_width>>1)+1;
}else{
steps = (1<<(p->max_depth - p->disp_depth - 2)) * p->node_width;
}
// 输出左侧节点
p->disp_column -= steps;
set_display_buffer(T, cur->left, p);
p->disp_column += steps;
// 输出右侧节点
if(p->disp_depth+1 == p->max_depth){
steps = p->node_width-steps;
}
p->disp_column += steps;
set_display_buffer(T, cur->right, p);
p->disp_column -= steps;
p->disp_depth--;
}
}
// 以图的形式展示红黑树
void rbtree_display(rbtree *T){
// 红黑树为空不画图
if(T->root_node == T->nil_node){
printf("rbtree DO NOT have any key!\n");
return;
}
// 初始化参数结构体
disp_parameters *para = (disp_parameters*)malloc(sizeof(disp_parameters));
if(para == NULL){
printf("disp_parameters struct malloc failed!");
return;
}
rbtree_node *max_node = rbtree_max(T, T->root_node);
para->max_num_width = decimal_width(max_node->key);
para->max_depth = rbtree_depth(T);
para->node_width = (para->max_num_width<=5) ? 7 : (para->max_num_width+2); // 边框“||”宽度2 + 数字宽度
para->disp_depth = 0;
para->disp_width = para->node_width * (1 << (para->max_depth-1)) + 1;
para->disp_column = ((para->disp_width-para->node_width)>>1);
int height = (para->max_depth-1)*3 + 2;
// 根据树的大小申请内存
para->disp_buffer = (char**)malloc(sizeof(char*)*height);
int i = 0;
for(i=0; i<height; i++){
para->disp_buffer[i] = (char*)malloc(sizeof(char)*para->disp_width);
memset(para->disp_buffer[i], ' ', para->disp_width);
para->disp_buffer[i][para->disp_width-1] = '\0';
}
// 打印内容
set_display_buffer(T, T->root_node, para);
for(i=0; i<height; i++){
printf("%s\n", para->disp_buffer[i]);
}
// 释放内存
for(i=0; i<height; i++){
free(para->disp_buffer[i]);
}
free(para->disp_buffer);
free(para);
}
// 检查当前红黑树的有效性:根节点黑色、红色不相邻、所有路径黑高相同
bool rbtree_check_effective(rbtree *T){
bool rc_flag = true; // 根节点黑色
bool rn_flag = true; // 红色不相邻
bool bh_flag = true; // 所有路径黑高相同
if(T->root_node->color == RED){
printf("ERROR! root-node's color is RED!\n");
rc_flag = false;
}else{
int depth = rbtree_depth(T);
int max_index_path = 1<<(depth-1); // 从根节点出发的路径总数
// 获取最左侧路径的黑高
int black_height = 0;
rbtree_node *cur = T->root_node;
while(cur != T->nil_node){
if(cur->color == BLACK) black_height++;
cur = cur->left;
// printf("bh = %d\n", black_height);
}
// 遍历每一条路径
int i_path = 0;
for(i_path=1; i_path<max_index_path; i_path++){
int dir = i_path;
int bh = 0; // 当前路径的黑高
cur = T->root_node;
while(cur != T->nil_node){
// 更新黑高
if(cur->color == BLACK){
bh++;
}
// 判断红色节点不相邻
else{
if((cur->left->color == RED) || (cur->right->color == RED)){
printf("ERROR! red node %d has red child!\n", cur->key);
rn_flag = false;
}
}
// 更新下一节点
// 0:left, 1:right
if(dir%2) cur = cur->right;
else cur = cur->left;
dir = dir>>1;
}
if(bh != black_height){
printf("ERROR! black height is not same! path 0 is %d, path %d is %d.\n", black_height, i_path, bh);
bh_flag = false;
}
}
}
return (rc_flag && rn_flag && bh_flag);
}
/*------------------------------------------------------------------------*/
/*-----------------------------下面为测试代码-------------------------------*/
#if RBTREE_DEBUG
#include<time.h> // 使用随机数
#include<sys/time.h> // 计算qps中获取时间
#define TIME_SUB_MS(tv1, tv2) ((tv1.tv_sec - tv2.tv_sec) * 1000 + (tv1.tv_usec - tv2.tv_usec) / 1000)
#define ENABLE_QPS 1 // 是否开启qps性能测试
#define continue_test_len 1000000 // 连续测试的长度
// 冒泡排序
void bubble_sort(int arr[], int len) {
int i, j, temp;
for (i = 0; i < len - 1; i++)
for (j = 0; j < len - 1 - i; j++)
if (arr[j] > arr[j + 1]) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
int main(){
/* --------------------定义数组-------------------- */
// 预定义的数组
// int KeyArray[20] = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20}; // 正着插
// int KeyArray[20] = {20,19,18,17,16,15,14,13,12,11,10,9,8,7,6,5,4,3,2,1}; // 倒着插
// int KeyArray[20] = {1,2,3,4,5,10,9,8,7,6,11,12,13,14,15,20,19,18,17,16}; // 乱序插
// int KeyArray[31] = {11,12,13,14,15,16,17,18,19,20,1,2,3,4,5,6,7,8,9,10,21,22,23,24,25,26,27,28,29,30,31}; // 乱序插
// 顺序增长的数组
int len_array = 18;
int KeyArray[len_array];
int i_array = 0;
for(i_array=0; i_array<len_array; i_array++){
KeyArray[i_array] = i_array + 1;
}
// // 随机生成固定大小的随机数组
// int len_array = 18;
// int KeyArray[len_array];
// srand(time(NULL));
// int i_array = 0;
// for(i_array=0; i_array<len_array; i_array++){
// KeyArray[i_array] = rand() % 9999999999;
// }
/* ------------------以下测试代码------------------ */
printf("-------------------红黑树插入测试------------------\n");
// 先给输入的数组排个序
int len_max = sizeof(KeyArray)/sizeof(int);
printf("测试数组长度: %d\n", len_max);
// 将原先的数组深拷贝并升序排序
int *KeyArray_sort = (int*)malloc(sizeof(KeyArray));
printf("RAND_MAX: %d\n", RAND_MAX);
int i = 0;
for(i = 0; i < len_max; i++){
KeyArray_sort[i] = KeyArray[i];
}
bubble_sort(KeyArray_sort, len_max);
// 申请红黑树内存
rbtree *T = rbtree_malloc();
// 依次插入数据
for(i = 0; i < len_max; i++){
rbtree_insert(T, KeyArray[i], NULL);
}
// 遍历数据,查看是否符合红黑树性质
// rbtree_display(T);
if(rbtree_check_effective(T)){
printf("PASS---->插入测试\n");
}else{
printf("FAIL---->插入测试\n");
}
// rbtree_display(T);
printf("-------------------红黑树前驱节点测试------------------\n");
int pass_flag = 1;
if(rbtree_precursor_node(T, rbtree_search(T, KeyArray_sort[0])) != T->nil_node){
printf("search first key %d's precursor error! get %d, expected nil_node\n", len_max, rbtree_precursor_node(T, rbtree_search(T, KeyArray_sort[0]))->key);
pass_flag = 0;
}
for(i = 1; i<len_max; i++){
rbtree_node *precursor = rbtree_precursor_node(T, rbtree_search(T, KeyArray_sort[i]));
if(precursor->key != KeyArray_sort[i-1]){
printf("search key %d error! get %d, expected %d\n", KeyArray_sort[i], precursor->key, KeyArray_sort[i-1]);
pass_flag = 0;
}
}
if(pass_flag){
printf("PASS---->前驱节点测试\n");
}else{
printf("FAIL---->前驱节点测试\n");
}
printf("-------------------红黑树后继节点测试------------------\n");
pass_flag = 1;
if(rbtree_successor_node(T, rbtree_search(T, KeyArray_sort[len_max-1])) != T->nil_node){
printf("search last key %d's successor error! get %d, expected nil_node\n",\
KeyArray_sort[len_max-1],\
rbtree_successor_node(T, rbtree_search(T, KeyArray_sort[len_max-1]))->key);
pass_flag = 0;
}
for(i = 0; i<len_max-1; i++){
rbtree_node *successor = rbtree_successor_node(T, rbtree_search(T, KeyArray_sort[i]));
if(successor->key != KeyArray_sort[i+1]){
printf("search key %d error! get %d, expected %d\n", KeyArray_sort[i], successor->key, KeyArray_sort[i+1]);
pass_flag = 0;
}
}
if(pass_flag){
printf("PASS---->后继节点测试\n");
}else{
printf("FAIL---->后继节点测试\n");
}
printf("-------------------红黑树删除测试------------------\n");
// 依次删除所有元素
for(i=0; i<len_max; i++){
rbtree_delete(T, rbtree_search(T, KeyArray_sort[i]));
if(!rbtree_check_effective(T)){
rbtree_display(T);
printf("FAIL---->删除测试%d\n", i+1);
break;
}else{
printf("PASS---->删除测试%d\n", i+1);
}
}
printf("-------------------红黑树打印测试------------------\n");
// 先插入数据1~18,再删除16/17/18,即可得到4层的满二叉树
for(i = 0; i < len_max; i++){
rbtree_insert(T, KeyArray[i], NULL);
}
for(i=0; i<3; i++){
rbtree_delete(T, rbtree_search(T, KeyArray_sort[len_max-i-1]));
if(!rbtree_check_effective(T)){
printf("FAIL---->删除测试%d\n", KeyArray_sort[len_max-i-1]);
break;
}else{
printf("PASS---->删除测试%d\n", KeyArray_sort[len_max-i-1]);
}
}
// 打印看看结果
rbtree_display(T);
// 清空红黑树
for(i=0; i<len_max; i++){
rbtree_delete(T, rbtree_search(T, KeyArray_sort[i]));
}
#if ENABLE_QPS
printf("---------------红黑树连续插入性能测试---------------\n");
// 定义时间结构体
struct timeval tv_begin;
struct timeval tv_end;
gettimeofday(&tv_begin, NULL);
for(i = 0; i < continue_test_len; i++){
rbtree_insert(T, i+1, NULL);
}
gettimeofday(&tv_end, NULL);
int time_ms = TIME_SUB_MS(tv_end, tv_begin);
float qps = (float)continue_test_len / (float)time_ms * 1000;
printf("total INSERTs:%d time_used:%d(ms) qps:%.2f(INSERTs/sec)\n", continue_test_len, time_ms, qps);
printf("---------------红黑树连续查找性能测试---------------\n");
gettimeofday(&tv_begin, NULL);
for(i = 0; i < continue_test_len; i++){
// rbtree_search(T, i+1);
if(rbtree_search(T, i+1)->key != i+1){
printf("continue_search error!\n");
return 0;
}
}
gettimeofday(&tv_end, NULL);
time_ms = TIME_SUB_MS(tv_end, tv_begin);
qps = (float)continue_test_len / (float)time_ms * 1000;
printf("total SEARCHs:%d time_used:%d(ms) qps:%.2f(SEARCHs/sec)\n", continue_test_len, time_ms, qps);
printf("---------------红黑树连续删除性能测试---------------\n");
gettimeofday(&tv_begin, NULL);
for(i = 0; i < continue_test_len; i++){
rbtree_delete(T, rbtree_search(T, i+1));
}
gettimeofday(&tv_end, NULL);
time_ms = TIME_SUB_MS(tv_end, tv_begin);
qps = (float)continue_test_len / (float)time_ms * 1000;
printf("total DELETEs:%d time_used:%d(ms) qps:%.2f(DELETEs/sec)\n", continue_test_len, time_ms, qps);
#endif
printf("--------------------------------------------------\n");
rbtree_free(T); // 别忘了释放内存
free(KeyArray_sort);
return 0;
}
#endif
测试代码输出结果
lyl@ubuntu:~/Desktop/kv-store/code_init$ gcc -o main rbtree_int.c
lyl@ubuntu:~/Desktop/kv-store/code_init$ ./main
-------------------红黑树插入测试------------------
测试数组长度: 18
RAND_MAX: 2147483647
PASS---->插入测试
-------------------红黑树前驱节点测试------------------
PASS---->前驱节点测试
-------------------红黑树后继节点测试------------------
PASS---->后继节点测试
-------------------红黑树删除测试------------------
PASS---->删除测试1
PASS---->删除测试2
PASS---->删除测试3
PASS---->删除测试4
PASS---->删除测试5
PASS---->删除测试6
PASS---->删除测试7
PASS---->删除测试8
PASS---->删除测试9
PASS---->删除测试10
PASS---->删除测试11
PASS---->删除测试12
PASS---->删除测试13
PASS---->删除测试14
PASS---->删除测试15
PASS---->删除测试16
PASS---->删除测试17
PASS---->删除测试18
-------------------红黑树打印测试------------------
PASS---->删除测试18
PASS---->删除测试17
PASS---->删除测试16
| 8 |
|BLACK|
/ \
| 4 | | 12 |
| RED | | RED |
/ \ / \
| 2 | | 6 | | 10 | | 14 |
|BLACK| |BLACK| |BLACK| |BLACK|
/ \ / \ / \ / \
| 1 || 3 || 5 || 7 || 9 || 11 || 13 || 15 |
|BLACK||BLACK||BLACK||BLACK||BLACK||BLACK||BLACK||BLACK|
There is NO key=16 in rbtree!
There is NO key=17 in rbtree!
There is NO key=18 in rbtree!
---------------红黑树连续插入性能测试---------------
total INSERTs:1000000 time_used:295(ms) qps:3389830.50(INSERTs/sec)
---------------红黑树连续查找性能测试---------------
total SEARCHs:1000000 time_used:118(ms) qps:8474576.00(SEARCHs/sec)
---------------红黑树连续删除性能测试---------------
total DELETEs:1000000 time_used:95(ms) qps:10526315.00(DELETEs/sec)
--------------------------------------------------
编程感想:
- 每一次旋转都是一次谋权篡位。
- 双旋的时候,最后的“当前节点”应该是原来的“祖父节点/父节点”,若还保留当前身份,那么会造成错误。
红黑树插入:
- 参考B站:【neko算法课】红黑树 插入【11期】
红黑树删除:
- 参考B站:【neko算法课】红黑树 删除【12期】
- 参考微信图文:图解:什么是二叉排序树?–介绍了标准BST删除操作
- 参考知乎:图解:红黑树删除篇(一文读懂)–里面的v对应del_r、u对应del_r_child
红黑树打印:
- 参考CSDN:二叉树生成与打印显示 c语言实现
2.4 btree的实现

一般来说,B树也是一个自平衡的二叉搜索树。但与红黑树不同的是,B树的节点可以存储多个元素, m m m阶B树的单个节点,最多有 m − 1 m-1 m−1 个元素、 m m m 个子节点。并且B树只有孩子节点、没有父节点(没有向上的指针)。也就是说,对于插入/删除操作,红黑树可以先从上往下寻找插入位置,再从下往上进行调整;而B树要先从上往下调整完(“分裂、合并/借位”),最后在叶子节点进行插入/删除,而没有从下往上的过程。即进行插入/删除时,B树从上往下只走一次。下面给出一个 m m m阶B树应该满足的条件(判断一棵B树是否有效的依据):
- 每个结点至多拥有 m m m颗子树。
- 根结点至少拥有两颗子树。
- 除了根结点以外,其余每个分支结点至少拥有 m / 2 m/2 m/2棵子树。
- 所有的叶结点都在同一层上。
- 有 k k k 棵子树的分支结点则存在 k − 1 k-1 k−1 个元素,元素按照递增顺序进行排序。
- 单个节点的元素数量 n n n 满足 ceil ( m / 2 ) − 1 ≤ n ≤ m − 1 \text{ceil}(m/2)-1 \le n \le m-1 ceil(m/2)−1≤n≤m−1。
B树可视化网站:https://www.cs.usfca.edu/~galles/visualization/BTree.html
同样的,B树的查找操作只需要从根节点不断比较即可,而B树的插入/删除逻辑如下:
B树插入:从上往下寻找要插入的叶子节点,过程中要下去的孩子若是满节点,则进行“分裂”。
- 分裂:取孩子的中间节点(第 ceil m 2 \text{ceil}\frac{m}{2} ceil2m 个)放上来,剩下的元素列变成两个子节点。
- 新元素必然添加到叶子节点上。
- 注意:只有根节点分裂会增加层高,其余的不会。
B树删除:从上往下寻找要删除元素的所在节点,过程中看情况进行“合并/借位”。若所在节点不是叶子节点,就将其换到叶子节点中。最后在叶子节点删除元素。
- 合并:从当前节点下放一个元素,然后该元素对应的两个子节点合并成一个子节点。团结就是力量。
- 借位:从当前节点下方一个元素到元素较少的孩子,然后从当前元素的另一个孩子节点拉上来一个元素取代位置,注意大小顺序。损有余而补不足。
// 遍历到叶子节点 while(不是叶子节点){ // 1. 确定下一节点和其兄弟节点 if(当前节点有要删除的元素) 哪边少哪边就是下一节点,当前元素对应的另一边就是兄弟节点。 else(当前节点没有要删除的元素) 确定好要去的下一节点后,左右两边谁多谁是兄弟节点。 // 2. 看是否需要调整 if(下一节点元素少){ if(孩子的兄弟节点元素多) 借位,进入下一节点。 else(孩子的兄弟节点元素少) 合并,进入合并后的节点。 }else if(下一节点元素多 && 当前节点有要删除元素){ if(下一节点是删除元素的左节点) 删除元素和其前驱元素换位,进入下一节点。 else(下一节点是删除元素的右节点) 删除元素和其后继元素换位,进入下一节点。 }else{ 直接进入下一节点。 } } // 然后在叶子节点删除元素注:判断孩子节点的元素少的条件是 元素数量 ≤ ceil m 2 − 1 \le \text{ceil}\frac{m}{2}-1 ≤ceil2m−1,判断元素多的条件是 元素数量 ≥ ceil m 2 \ge\text{ceil}\frac{m}{2} ≥ceil2m。
根据上述原理,我使用C语言实现了B树完整的增删查操作,并增加了检验有效性、打印B树的代码,以及测试代码(终端显示进度条)。同样为了加快开发速度,预设“键值对”的类型为int key、void* value,后续将B树添加进“kv存储协议”中时会进一步修改:
btree_int.c-共989行
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<stdbool.h>
// 编译指令:gcc -o main 1-1btree.c
// 本代码实现M阶B树,存储int型key,未定义value。
#define BTREE_DEBUG 1 // 是否运行测试代码
typedef struct _btree_node{
int *keys;
void *values;
struct _btree_node **children;
int num; // 当前节点的实际元素数量
int leaf; // 当前节点是否为叶子节点
}btree_node;
typedef struct _btree{
int m; // m阶B树
struct _btree_node *root_node;
}btree;
/*
下面是所有的函数声明,排列顺序与源代码调用相同,最外层的函数放在最下面。
*/
/*----初始化分配内存----*/
// 创建单个节点,leaf表示是否为叶子节点
btree_node *btree_node_create(btree *T, int leaf);
// 初始化m阶B树:分配内存,最后记得销毁B树btree_destroy()
btree *btree_init(int m);
/*----释放内存----*/
// 删除单个节点
void btree_node_destroy(btree_node *cur);
// 递归删除给定节点作为根节点的子树
void btree_node_destroy_recurse(btree_node *cur);
// 删除所有节点,释放btree内存
btree *btree_destroy(btree *T);
/*----插入操作----*/
// 根节点分裂
btree_node* btree_root_split(btree *T);
// 索引为idx的孩子节点分裂
btree_node* btree_child_split(btree *T, btree_node* cur, int idx);
// btree插入元素:先分裂,再插入,必然在叶子节点插入
void btree_insert_key(btree *T, int key);
/*----删除操作----*/
// 借位:将cur节点的idx_key元素下放到idx_dest孩子
btree_node *btree_borrow(btree_node *cur, int idx_key, int idx_dest);
// 合并:将cur节点的idx元素向下合并
btree_node *btree_merge(btree *T, btree_node *cur, int idx);
// 找出当前节点索引为idx_key的元素的前驱节点
btree_node* btree_precursor_node(btree *T, btree_node *cur, int idx_key);
// 找出当前节点索引为idx_key的元素的后继节点
btree_node* btree_successor_node(btree *T, btree_node *cur, int idx_key);
// btree删除元素:先合并/借位,再删除,必然在叶子节点删除
void btree_delete_key(btree *T, int key);
/*----查找操作----*/
// 查找key
btree_node* btree_search_key(btree *T, int key);
/*----打印信息----*/
// 打印当前节点信息
void btree_node_print(btree_node *cur);
// 先序遍历给定节点为根节点的子树(递归)
void btree_traversal_node(btree *T, btree_node *cur);
// btree遍历
void btree_traversal(btree *T);
/*----检查有效性----*/
// 获取B树的高度
int btree_depth(btree *T);
// 检查给定节点的有效性
// 键值:根节点至少有一个key,其余节点至少有ceil(m/2)-1个key
// 分支:所有节点数目子树为当前节点元素数量+1
bool btree_node_check_effective(btree *T, btree_node *cur);
// 遍历所有路径检查m阶B树的有效性
// 平衡性:所有叶节点都在同一层(所有路径高度相等)
// 有序性:所有元素升序排序
// 键值:根节点至少有一个key,其余节点至少有ceil(m/2)-1个key
// 分支:所有节点数目子树为当前节点元素数量+1
bool btree_check_effective(btree *T);
/*-----------------------------下面为函数定义-------------------------------*/
// 创建单个节点,leaf表示是否为叶子节点
btree_node *btree_node_create(btree *T, int leaf){
btree_node *new = (btree_node*)malloc(sizeof(btree_node));
if(new == NULL){
printf("btree node malloc failed!\n");
return NULL;
}
new->keys = (int*)calloc(T->m-1, sizeof(int));
new->values = (void*)calloc(T->m-1, sizeof(void));
new->children = (btree_node **)calloc(T->m, sizeof(btree_node*));
new->num = 0;
new->leaf = leaf;
return new;
}
// 删除单个节点
void btree_node_destroy(btree_node *cur){
free(cur->keys);
free(cur->values);
free(cur->children);
free(cur);
}
// 初始化m阶B树:分配内存,最后记得销毁B树btree_destroy()
btree *btree_init(int m){
btree *T = (btree*)malloc(sizeof(btree));
if(T == NULL){
// 只有内存不够时才会分配失败
printf("rbtree malloc failed!\n");
return NULL;
}
T->m = m;
T->root_node = NULL;
}
// 递归删除给定节点作为根节点的子树
void btree_node_destroy_recurse(btree_node *cur){
int i = 0;
if(cur->leaf == 1){
btree_node_destroy(cur);
}else{
for(i=0; i<cur->num+1; i++){
btree_node_destroy_recurse(cur->children[i]);
}
}
}
// 释放btree内存
btree *btree_destroy(btree *T){
// 删除所有节点
if(T->root_node != NULL){
btree_node_destroy_recurse(T->root_node);
}
// 删除btree
free(T);
}
// 根节点分裂
btree_node* btree_root_split(btree *T){
// 创建兄弟节点
btree_node *brother = btree_node_create(T, T->root_node->leaf);
int i = 0;
for(i=0; i<((T->m-1)>>1); i++){
brother->keys[i] = T->root_node->keys[i+(T->m>>1)];
T->root_node->keys[i+(T->m>>1)] = 0;
brother->children[i] = T->root_node->children[i+(T->m>>1)];
T->root_node->children[i+(T->m>>1)] = NULL;
brother->num++;
T->root_node->num--;
}
// 还需要复制最后一个指针
brother->children[brother->num] = T->root_node->children[T->m-1];
T->root_node->children[T->m-1] = NULL;
// 创建新的根节点
btree_node *new_root = btree_node_create(T, 0);
new_root->keys[0] = T->root_node->keys[T->root_node->num-1];
T->root_node->keys[T->root_node->num-1] = 0;
T->root_node->num--;
new_root->num = 1;
new_root->children[0] = T->root_node;
new_root->children[1] = brother;
T->root_node = new_root;
return T->root_node;
}
// 索引为idx的孩子节点分裂
btree_node* btree_child_split(btree *T, btree_node* cur, int idx){
// 创建孩子的兄弟节点
btree_node *full_child = cur->children[idx];
btree_node *new_child = btree_node_create(T, cur->children[idx]->leaf);
int i = 0;
for(i=0; i<((T->m-1)>>1); i++){
new_child->keys[i] = full_child->keys[i+(T->m>>1)];
full_child->keys[i+(T->m>>1)] = 0;
new_child->children[i] = full_child->children[i+(T->m>>1)];
full_child->children[i+(T->m>>1)] = NULL;
new_child->num++;
full_child->num--;
}
new_child->children[new_child->num] = full_child->children[T->m-1];
full_child->children[T->m-1] = NULL;
// 把孩子的元素拿上来
// 调整自己的key和children
for(i=cur->num; i>idx; i--){
cur->keys[i] = cur->keys[i-1];
cur->children[i+1] = cur->children[i];
}
cur->children[idx+1] = new_child;
cur->keys[idx] = full_child->keys[full_child->num-1];
full_child->keys[full_child->num-1] = 0;
cur->num++;
full_child->num--;
return cur;
}
// btree插入元素:先分裂,再插入,必然在叶子节点插入
void btree_insert_key(btree *T, int key){
btree_node *cur = T->root_node;
if(key <= 0){
// printf("illegal insert: key=%d!\n", key);
}else if(cur == NULL){
btree_node *new = btree_node_create(T, 1);
new->keys[0] = key;
new->num = 1;
T->root_node = new;
}else{
// 函数整体逻辑:从根节点逐步找到元素要插入的叶子节点,先分裂、再添加
// 先查看根节点是否需要分裂
if(cur->num == T->m-1){
cur = btree_root_split(T);
}
// 从根节点开始寻找要插入的叶子节点
while(cur->leaf == 0){
// 找到下一个要比较的孩子节点
int next_idx = 0; // 要进入的孩子节点的索引
int i = 0;
for(i=0; i<cur->num; i++){
if(key == cur->keys[i]){
// printf("insert failed! already has key=%d!\n", key);
return;
}else if(key < cur->keys[i]){
next_idx = i;
break;
}else if(i == cur->num-1){
next_idx = cur->num;
}
}
// 查看孩子是否需要分裂,不需要就进入
if(cur->children[next_idx]->num == T->m-1){
cur = btree_child_split(T, cur, next_idx);
}else{
cur = cur->children[next_idx];
}
}
// 将新元素插入到叶子节点中
int i = 0;
int pos = 0; // 要插入的位置
for(i=0; i<cur->num; i++){
if(key == cur->keys[i]){
// printf("insert failed! already has key=%d!\n", key);
return;
}else if(key < cur->keys[i]){
pos = i;
break;
}else if(i == cur->num-1){
pos = cur->num;
}
}
// 插入元素
if(pos == cur->num){
cur->keys[cur->num] = key;
}else{
for(i=cur->num; i>pos; i--){
cur->keys[i] = cur->keys[i-1];
}
cur->keys[pos] = key;
}
cur->num++;
}
}
// 借位:将cur节点的idx_key元素下放到idx_dest孩子
btree_node *btree_borrow(btree_node *cur, int idx_key, int idx_dest){
int idx_sour = (idx_key == idx_dest) ? idx_dest+1 : idx_key;
btree_node *node_dest = cur->children[idx_dest]; // 目的节点
btree_node *node_sour = cur->children[idx_sour]; // 源节点
if(idx_key == idx_dest){
// 自己下去作为目的节点的最后一个元素
node_dest->keys[node_dest->num] = cur->keys[idx_key];
node_dest->children[node_dest->num+1] = node_sour->children[0];
node_dest->num++;
// 把源节点的第一个元素请上来
cur->keys[idx_key] = node_sour->keys[0];
for(int i=0; i<node_sour->num-1; i++){
node_sour->keys[i] = node_sour->keys[i+1];
node_sour->children[i] = node_sour->children[i+1];
}
node_sour->children[node_sour->num-1] = node_sour->children[node_sour->num];
node_sour->children[node_sour->num] = NULL;
node_sour->keys[node_sour->num-1] = 0;
node_sour->num--;
}else{
// 自己下去作为目的节点的第一个元素
node_dest->children[node_dest->num+1] = node_dest->children[node_dest->num];
for(int i=node_dest->num; i>0; i--){
node_dest->keys[i] = node_dest->keys[i-1];
node_dest->children[i] = node_dest->children[i-1];
}
node_dest->keys[0] = cur->keys[idx_key];
node_dest->children[0] = node_sour->children[node_sour->num];
node_dest->num++;
// 把源节点的最后一个元素请上来
cur->keys[idx_key] = node_sour->keys[node_sour->num-1];
node_sour->keys[node_sour->num-1] = 0;
node_sour->children[node_sour->num] = NULL;
node_sour->num--;
}
return node_dest;
}
// 合并:将cur节点的idx元素向下合并
btree_node *btree_merge(btree *T, btree_node *cur, int idx){
btree_node *left = cur->children[idx];
btree_node *right = cur->children[idx+1];
// 自己下去左孩子,调整当前节点
left->keys[left->num] = cur->keys[idx];
left->num++;
for(int i=idx; i<cur->num-1; i++){
cur->keys[i] = cur->keys[i+1];
cur->children[i+1] = cur->children[i+2];
}
cur->keys[cur->num-1] = 0;
cur->children[cur->num] = NULL;
cur->num--;
// 右孩子复制到左孩子
for(int i=0; i<right->num; i++){
left->keys[left->num] = right->keys[i];
left->children[left->num] = right->children[i];
left->num++;
}
left->children[left->num] = right->children[right->num];
// 删除右孩子
btree_node_destroy(right);
// 更新根节点
if(T->root_node == cur){
btree_node_destroy(cur);
T->root_node = left;
}
return left;
}
// 找出当前节点索引为idx_key的元素的前驱节点
btree_node* btree_precursor_node(btree *T, btree_node *cur, int idx_key){
if(cur->leaf == 0){
cur = cur->children[idx_key];
while(cur->leaf == 0){
cur = cur->children[cur->num];
}
}
return cur;
}
// 找出当前节点索引为idx_key的元素的后继节点
btree_node* btree_successor_node(btree *T, btree_node *cur, int idx_key){
if(cur->leaf == 0){
cur = cur->children[idx_key+1];
while(cur->leaf == 0){
cur = cur->children[0];
}
}
return cur;
}
// btree删除元素:先合并/借位,再删除,必然在叶子节点删除
void btree_delete_key(btree *T, int key){
if(T->root_node!=NULL && key>0){
btree_node *cur = T->root_node;
// 在去往叶子节点的过程中不断调整(合并/借位)
while(cur->leaf == 0){
// 看看要去哪个孩子
int idx_next = 0; //下一个要去的孩子节点索引
int idx_bro = 0;
int idx_key = 0;
if(key < cur->keys[0]){
idx_next = 0;
idx_bro = 1;
}else if(key > cur->keys[cur->num-1]){
idx_next = cur->num;
idx_bro = cur->num-1;
}else{
for(int i=0; i<cur->num; i++){
if(key == cur->keys[i]){
// 哪边少去哪边
if(cur->children[i]->num <= cur->children[i+1]->num){
idx_next = i;
idx_bro = i+1;
}else{
idx_next = i+1;
idx_bro = i;
}
break;
}else if((i<cur->num-1) && (key > cur->keys[i]) && (key < cur->keys[i+1])){
idx_next = i + 1;
// 谁多谁是兄弟
if(cur->children[i]->num > cur->children[i+2]->num){
idx_bro = i;
}else{
idx_bro = i+2;
}
break;
}
}
}
idx_key = (idx_next < idx_bro) ? idx_next : idx_bro;
// 依据孩子节点的元素数量进行调整
if(cur->children[idx_next]->num <= ((T->m>>1)-1)){
// 借位:下一孩子的元素少,下一孩子的兄弟节点的元素多
if(cur->children[idx_bro]->num >= (T->m>>1)){
cur = btree_borrow(cur, idx_key, idx_next);
}
// 合并:两个孩子都不多
else{
cur = btree_merge(T, cur, idx_key);
}
}else if(cur->keys[idx_key] == key){
// 若当前元素就是要删除的节点,那一定要送下去
// 但是不能借位,而是将前驱元素搬上来
btree_node* pre;
int tmp;
if(idx_key == idx_next){
// 找到前驱节点
pre = btree_precursor_node(T, cur, idx_key);
// 交换 当前元素 和 前驱节点的最后一个元素
tmp = pre->keys[pre->num-1];
pre->keys[pre->num-1] = cur->keys[idx_key];
cur->keys[idx_key] = tmp;
}else{
// 找到后继节点
pre = btree_successor_node(T, cur, idx_key);
// 交换 当前元素 和 后继节点的第一个元素
tmp = pre->keys[0];
pre->keys[0] = cur->keys[idx_key];
cur->keys[idx_key] = tmp;
}
cur = cur->children[idx_next];
// cur = btree_borrow(cur, idx_key, idx_next);
}else{
cur = cur->children[idx_next];
}
}
// 叶子节点删除元素
for(int i=0; i<cur->num; i++){
if(cur->keys[i] == key){
if(cur->num == 1){
// 若B树只剩最后一个元素
btree_node_destroy(cur);
T->root_node = NULL;
}else{
if(i != cur->num-1){
for(int j=i; j<(cur->num-1); j++){
cur->keys[j] = cur->keys[j+1];
}
}
cur->keys[cur->num-1] = 0;
cur->num--;
}
}
// else if(i == cur->num-1){
// printf("there is no key=%d\n", key);
// }
}
}
}
// 打印当前节点信息
void btree_node_print(btree_node *cur){
if(cur == NULL){
printf("NULL\n");
}else{
printf("leaf:%d, num:%d, key:|", cur->leaf, cur->num);
for(int i=0; i<cur->num; i++){
printf("%d|", cur->keys[i]);
}
printf("\n");
}
}
// 先序遍历给定节点为根节点的子树(递归)
void btree_traversal_node(btree *T, btree_node *cur){
// 打印当前节点信息
btree_node_print(cur);
// 依次打印所有子节点信息
if(cur->leaf == 0){
int i = 0;
for(i=0; i<cur->num+1; i++){
btree_traversal_node(T, cur->children[i]);
}
}
}
// btree遍历
void btree_traversal(btree *T){
if(T->root_node != NULL){
btree_traversal_node(T, T->root_node);
}else{
// printf("btree_traversal(): There is no key in B-tree!\n");
}
}
// 查找key
btree_node* btree_search_key(btree *T, int key){
if(key > 0){
btree_node *cur = T->root_node;
// 先寻找是否为非叶子节点
while(cur->leaf == 0){
if(key < cur->keys[0]){
cur = cur->children[0];
}else if(key > cur->keys[cur->num-1]){
cur = cur->children[cur->num];
}else{
for(int i=0; i<cur->num; i++){
if(cur->keys[i] == key){
return cur;
}else if((i<cur->num-1) && (key > cur->keys[i]) && (key < cur->keys[i+1])){
cur = cur->children[i+1];
}
}
}
}
// 在寻找是否为叶子节点
if(cur->leaf == 1){
for(int i=0; i<cur->num; i++){
if(cur->keys[i] == key){
return cur;
}
}
}
}
// 都没找到返回NULL
return NULL;
}
// 获取B树的高度
int btree_depth(btree *T){
int depth = 0;
btree_node *cur = T->root_node;
while(cur != NULL){
depth++;
cur = cur->children[0];
}
return depth;
}
// 检查给定节点的有效性
// 键值:根节点至少有一个key,其余节点至少有ceil(m/2)-1个key
// 分支:所有节点数目子树为当前节点元素数量+1
bool btree_node_check_effective(btree *T, btree_node *cur){
bool eff_flag = true;
// 统计键值和子节点数量
int num_kvs = 0, num_child = 0;
int i = 0;
while(cur->keys[i] != 0){
// 判断元素是否递增
if(i>=1 && (cur->keys[i] <= cur->keys[i-1])){
printf("ERROR! the following node DOT sorted!\n");
btree_node_print(cur);
eff_flag = false;
break;
}
// 统计数量
num_kvs++;
i++;
}
i = 0;
while(cur->children[i] != NULL){
// 子节点和当前节点的有序性
if(i<num_kvs){
if(cur->keys[i] <= cur->children[i]->keys[cur->children[i]->num]){
printf("ERROR! the follwing node's child[%d] has bigger key=%d than %d\n", i, cur->children[i]->keys[cur->children[i]->num], cur->keys[i]);
printf("follwing node--");
btree_node_print(cur);
printf(" error child--");
btree_node_print(cur->children[i]);
eff_flag = false;
}else if(cur->keys[i] >= cur->children[i+1]->keys[0]){
printf("ERROR! the follwing node's child[%d] has smaller key=%d than %d\n", i+1, cur->children[i+1]->keys[0], cur->keys[i]);
printf("follwing node--");
btree_node_print(cur);
printf(" error child--");
btree_node_print(cur->children[i+1]);
eff_flag = false;
}
}
// 统计数量
num_child++;
i++;
}
// 判断元素数量是否合理
if(cur->num >= T->m){
printf("ERROR! the follwing node has too much keys:%d(at most %d)\n", cur->num, T->m-1);
btree_node_print(cur);
eff_flag = false;
}
if((cur != T->root_node) && (num_kvs<((T->m>>1)-1))){
printf("ERROR! the follwing node has too few keys:%d(at least %d)\n", num_kvs, (T->m>>1)-1);
btree_node_print(cur);
eff_flag = false;
}
if(num_kvs != cur->num){
printf("ERROR! the follwing node has %d keys but num=%d\n", num_kvs, cur->num);
btree_node_print(cur);
eff_flag = false;
}
if((cur->leaf == 0) && (num_child != cur->num+1)){
printf("ERROR! the follwing node has %d keys but %d child(except keys+1=child)\n", num_kvs, num_child);
btree_node_print(cur);
eff_flag = false;
}
return eff_flag;
}
// 遍历所有路径检查m阶B树的有效性
// 平衡性:所有叶节点都在同一层(所有路径高度相等)
// 有序性:所有元素升序排序
// 键值:根节点至少有一个key,其余节点至少有ceil(m/2)-1个key
// 分支:所有节点数目子树为当前节点元素数量+1
bool btree_check_effective(btree *T){
bool effe_flag = true;
int depth = btree_depth(T);
if(depth == 0){
// printf("btree_check_effective(): There is no key in B-tree!\n");
}else if(depth == 1){
// 只有一个根节点
effe_flag = btree_node_check_effective(T, T->root_node);
}else{
// 最大的可能路径数量
int max_path = 1;
int depth_ = depth-1;
while(depth_ != 0){
max_path *= T->m;
depth_--;
}
// 遍历所有路径(每个路径对应一个叶子节点)
btree_node *cur = T->root_node;
int i_path = 0;
for(i_path=0; i_path<max_path; i_path++){
int dir = i_path; // 本次路径的方向控制
int i_height = 0; // 本次路径的高度
int i_effe = 1; // 指示是否存在本路径
cur = T->root_node;
while(cur != NULL){
// 当前节点的有效性
effe_flag = btree_node_check_effective(T, cur);
if(!effe_flag) break;
// 更新高度
i_height++;
// 更新下一节点
if(cur->children[dir%T->m]==NULL && !cur->leaf){
i_effe = 0;
break;
}
cur = cur->children[dir%T->m];
dir /= T->m;
}
// if(btree_node_check_effective(T, cur))
// 判断本路径节点数(高度)
if(i_height != depth && i_effe){
printf("ERROR! not all leaves in the same layer! the leftest path's height=%d, while the %dst path's height=%d.\n",
depth, i_path, i_height);
effe_flag = false;
}
if(!effe_flag) break;
}
}
return effe_flag;
}
/*-----------------------------下面为测试代码-------------------------------*/
#if BTREE_DEBUG
#include<time.h> // 使用随机数
#include<sys/time.h> // 计算qps中获取时间
#define TIME_SUB_MS(tv1, tv2) ((tv1.tv_sec - tv2.tv_sec) * 1000 + (tv1.tv_usec - tv2.tv_usec) / 1000)
#define ENABLE_QPS 1 // 是否开启qps性能测试
#define continue_test_len 10000000 // 连续测试的长度
// 冒泡排序
void bubble_sort(int arr[], int len) {
int i, j, temp;
for (i = 0; i < len - 1; i++)
for (j = 0; j < len - 1 - i; j++)
if (arr[j] > arr[j + 1]) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
// 打印当前数组
void print_int_array(int* KeyArray, int len_array){
printf("测试数组为KeyArray[%d] = {", len_array);
for(int i=0; i<len_array; i++){
if(i == len_array-1){
printf("%d", KeyArray[i]);
}else{
printf("%d, ", KeyArray[i]);
}
}
printf("}\n");
}
int main(){
// 定义
/* --------------------定义数组-------------------- */
// 预定义的数组
// int KeyArray[20] = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20}; // 正着插
// int KeyArray[20] = {20,19,18,17,16,15,14,13,12,11,10,9,8,7,6,5,4,3,2,1}; // 倒着插
// int KeyArray[20] = {1,2,3,4,5,10,9,8,7,6,11,12,13,14,15,20,19,18,17,16}; // 乱序插
// int KeyArray[31] = {11,12,13,14,15,16,17,18,19,20,1,2,3,4,5,6,7,8,9,10,21,22,23,24,25,26,27,28,29,30,31}; // 乱序插
// int KeyArray[18] = {18,8,13,9,13,0,7,13,14,7,1,7,19,7,9,18,17,18}; // 乱序插
// // 顺序增长的数组
// int len_array = 26;
// int KeyArray[len_array];
// int i_array = 0;
// for(i_array=0; i_array<len_array; i_array++){
// KeyArray[i_array] = i_array + 1;
// }
// // 随机生成固定大小的随机数组
// int len_array = 18;
// int KeyArray[len_array];
// srand(time(NULL));
// int i_array = 0;
// for(i_array=0; i_array<len_array; i_array++){
// // KeyArray[i_array] = rand() % 9999999999;
// KeyArray[i_array] = rand() % 20;
// }
// printf("RAND_MAX: %d\n", RAND_MAX);
/* ------------------以下测试代码------------------ */
// printf("-------------------B树插入测试------------------\n");
// // 先给输入的数组排个序
// int len_max = sizeof(KeyArray)/sizeof(int);
// printf("测试数组长度: %d\n", len_max);
// // 将原先的数组深拷贝并升序排序
// int *KeyArray_sort = (int*)malloc(sizeof(KeyArray));
// int i = 0;
// for(i = 0; i < len_max; i++){
// KeyArray_sort[i] = KeyArray[i];
// }
// bubble_sort(KeyArray_sort, len_max);
int max_test = 100; // 测试的总次数
int len_array = 1000; // 单次测试的数组长度
bool detail_flag = false; // 是否打印详细信息
bool pass_flag = true;
printf("---------------------常规测试---------------------\n");
for(int i_test=0; i_test<max_test; i_test++){
// 随机生成固定大小的随机数组
int KeyArray[len_array];
srand(time(NULL));
for(int i_array=0; i_array<len_array; i_array++){
// KeyArray[i_array] = rand() % 9999999999;
KeyArray[i_array] = rand() % len_array;
}
// int KeyArray[10000] = {};
// 申请红黑树内存
btree *T = btree_init(6);
btree *T_old = btree_init(6);
if(detail_flag){
printf("--------------------开始测试--------------------\n");
print_int_array(KeyArray, len_array);
}
if(detail_flag){
printf("-------------------B树插入测试------------------\n");
}
/*-------------------B树插入测试------------------*/
// 依次插入数据,并检查有效性
for(int i=0; i<len_array; i++){
if(i>0){
btree_insert_key(T_old, KeyArray[i-1]);
}
btree_insert_key(T, KeyArray[i]);
// 方便打印调试
// if(i==65){
// printf("Before insert the %2d's key=%d:\n", i+1, KeyArray[i]);
// btree_traversal(T_old);
// printf("After insert the %2d's key=%d:\n", i+1, KeyArray[i]);
// btree_traversal(T);
// }
if(btree_check_effective(T)==false){
printf("after insert KeyArray[%d]=%d error!\n", i, KeyArray[i]);
pass_flag = false;
break;
}
}
if(pass_flag){
if(detail_flag) printf("PASS---->插入测试%d/%d\n", i_test+1, max_test);
btree_insert_key(T_old, KeyArray[len_array]);
}else{
if(detail_flag) printf("FAIL---->插入测试%d/%d\n", i_test+1, max_test);
// printf("Before insert:\n");
// btree_traversal(T_old);
// printf("After insert:\n");
// btree_traversal(T);
btree_destroy(T_old);
btree_destroy(T);
break;
}
if(detail_flag){
btree_traversal(T);
printf("\n");
}
if(detail_flag){
printf("-------------------B树查找测试------------------\n");
}
/*-------------------B树查找测试------------------*/
btree_node* sear = NULL;
for(int i=0; i<len_array; i++){
if(KeyArray[i] > 0){
sear = btree_search_key(T, KeyArray[i]);
pass_flag = false;
if(sear != NULL){
for(int j=0; j<sear->num; j++){
if(sear->keys[j] == KeyArray[i]){
pass_flag = true;
break;
}
}
}
if(detail_flag){
printf("search KeyArray[%d]=%d ----> ", i, KeyArray[i]);
btree_node_print(sear);
}
}
if(pass_flag == false){
print_int_array(KeyArray, len_array); // 打印当前数组
printf("following node DOT has KeyArray[%d]=%d!\n", i, KeyArray[i]);
btree_node_print(sear);
pass_flag = false;
break;
}
}
if(pass_flag){
if(detail_flag) printf("PASS---->查找测试%d/%d\n", i_test+1, max_test);
}else{
printf("FAIL---->查找测试%d/%d\n", i_test+1, max_test);
break;
}
if(detail_flag){
printf("-------------------B树删除测试------------------\n");
}
/*-------------------B树删除测试------------------*/
for(int i=0; i<len_array; i++){
// if(i==496){
// // 加一句打印方便调试暂停
// printf("Now delete KeyArray[%d]=%d:\n", i, KeyArray[i]);
// }
if(i>0){
btree_delete_key(T_old, KeyArray[i-1]);
}
btree_delete_key(T, KeyArray[i]);
if(detail_flag){
printf("delete KeyArray[%d]=%d:\n", i, KeyArray[i]);
btree_traversal(T);
}
if(btree_check_effective(T) == false){
print_int_array(KeyArray, len_array); // 打印当前数组
printf("after delete KeyArray[%d]=%d error!\n", i, KeyArray[i]);
pass_flag = false;
break;
}
}
if(pass_flag){
if(detail_flag) printf("PASS---->删除测试%d/%d\n", i_test+1, max_test);
}else{
printf("FAIL---->删除测试%d/%d\n", i_test+1, max_test);
// printf("Before delete:\n");
// btree_traversal(T_old);
// printf("After delete:\n");
// btree_traversal(T);
btree_destroy(T_old);
btree_destroy(T);
break;
}
if(detail_flag){
printf("--------------------------------------------------\n");
}
btree_destroy(T_old);
btree_destroy(T);
// 整点进度条看看
if(pass_flag){
// printf("PASS----> WHOLE TEST %d/%d!\r", i_test+1, max_test);
int bar_process; // 编译器初始化为0
bool already_print_txt; // 编译器初始化为false
bool already_print_bar; // 编译器初始化为false
const int len_bar = 20; // 完整进度条的长度
// 打印进度条前面的说明
if(!already_print_txt){
printf("PASS TEST PROCESS: ");
fflush(stdout);
}
already_print_txt = true;
// 打印进度条
if(len_bar*(i_test+1)/max_test > bar_process){
// 光标往前回退
if(already_print_bar){
printf("\033[4D"); // ANSI转义序列
}
// 画出进度条
for(int i=0; i<(len_bar*(i_test+1)/max_test - bar_process); i++){
printf("█");
fflush(stdout);
}
// 显示进度范围
printf(" %d%%", 100*(i_test+1)/max_test);
fflush(stdout);
already_print_bar = true;
bar_process = len_bar*(i_test+1)/max_test;
if(i_test+1 == max_test) printf("\n");
}
}
}
// 只是为了最后一行判断用
if(pass_flag){
// printf("\r\033[K"); // 清除本行
printf("PASS----> ALL %d TEST!\n", max_test);
}
printf("--------------------------------------------------\n");
printf("---------------------性能测试---------------------\n");
btree* bT = btree_init(16); // 初始化16阶B树
// 定义时间结构体
struct timeval tv_begin;
struct timeval tv_end;
// 插入性能测试
gettimeofday(&tv_begin, NULL);
for(int i=0; i<continue_test_len; i++){
btree_insert_key(bT, i+1);
}
gettimeofday(&tv_end, NULL);
int time_ms = TIME_SUB_MS(tv_end, tv_begin);
float qps = (float)continue_test_len / (float)time_ms * 1000;
printf("total INSERTs:%d time_used:%d(ms) qps:%.2f(INSERTs/sec)\n", continue_test_len, time_ms, qps);
// 查找性能测试
gettimeofday(&tv_begin, NULL);
for(int i=0; i<continue_test_len; i++){
btree_node* node = btree_search_key(bT, i+1);
int idx = 0;
for(idx=0; idx<node->num; idx++){
if(node->keys[idx] == i+1){
break;
}
}
if(idx == node->num){
printf("continue_search error!\n");
return 0;
}
}
gettimeofday(&tv_end, NULL);
time_ms = TIME_SUB_MS(tv_end, tv_begin);
qps = (float)continue_test_len / (float)time_ms * 1000;
printf("total SEARCHs:%d time_used:%d(ms) qps:%.2f(SEARCHs/sec)\n", continue_test_len, time_ms, qps);
// // 删除性能测试
// gettimeofday(&tv_begin, NULL);
// for(int i=0; i<continue_test_len; i++){
// btree_delete_key(bT, i+1);
// }
// gettimeofday(&tv_end, NULL);
// time_ms = TIME_SUB_MS(tv_end, tv_begin);
// qps = (float)continue_test_len / (float)time_ms * 1000;
// printf("total DELETEs:%d time_used:%d(ms) qps:%.2f(DELETEs/sec)\n", continue_test_len, time_ms, qps);
// 销毁B树
btree_destroy(bT);
printf("--------------------------------------------------\n");
return 0;
}
#endif
测试代码输出结果----记得测一下连续读、查、删的速度
lyl@ubuntu:~/Desktop/kv-store/code_init$ gcc -o main btree_int.c
lyl@ubuntu:~/Desktop/kv-store/code_init$ ./main
---------------------常规测试---------------------
PASS TEST PROCESS: ███████████████████ 100%
PASS----> ALL 100 TEST!
--------------------------------------------------
---------------------性能测试---------------------
total INSERTs:10000000 time_used:2379(ms) qps:4203447.00(INSERTs/sec)
total SEARCHs:10000000 time_used:1007(ms) qps:9930486.00(SEARCHs/sec)
total DELETEs:10000000 time_used:18(ms) qps:555555584.00(DELETEs/sec)
--------------------------------------------------
未解决bug:测试代码的最后如果多加上一个“删除性能测试”,就不显示进度条了?很奇怪
参考内容:
- B站:【CS61B汉化】七海讲数据结构-平衡树&B树–B树的插入–超可爱的视频
- 知乎:从B树中删除一个关键字–主要参考了孩子元素多的时候怎么删除
- B站:可视化数据结构-B+树–插入数据的动画很清晰
2.5 hash的实现
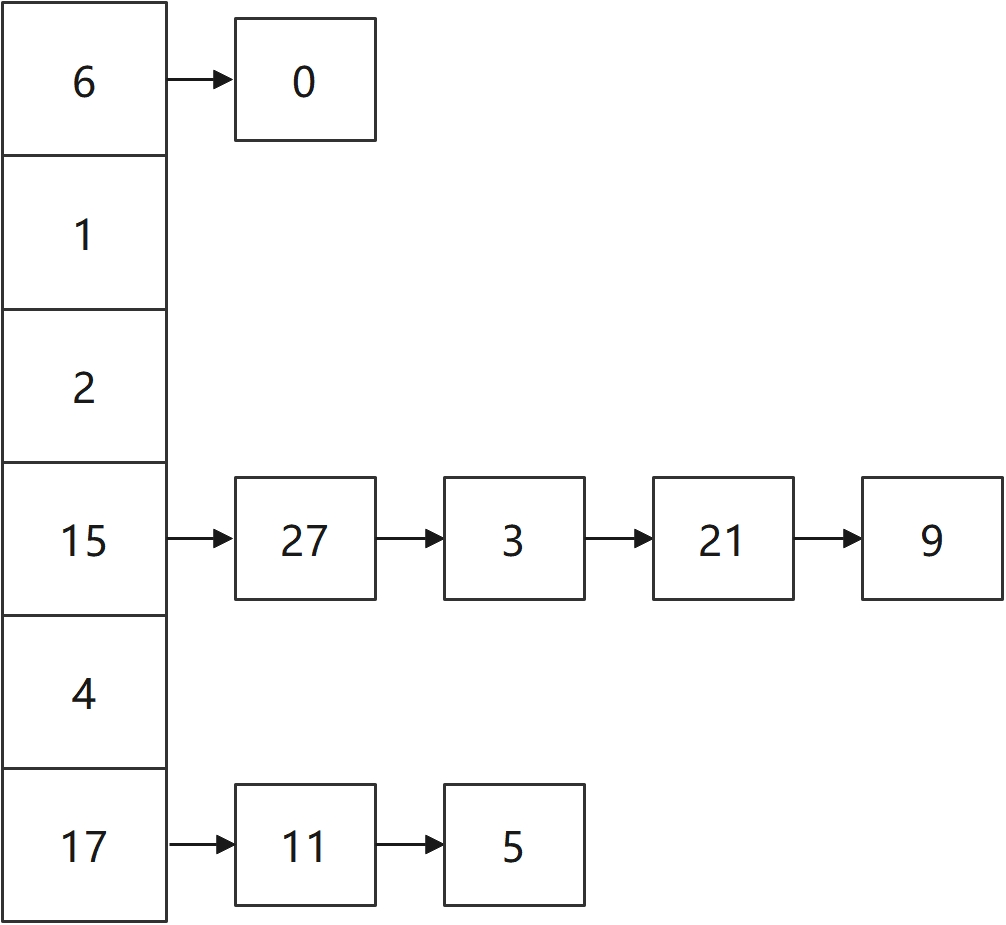
终于度过了本项目所有最难的部分,下面的内容都比较简单。链式哈希的增删查操作简洁明了。链式哈希首先会声明一个固定长度的哈希表(如1024),若需要插入新元素时,首先计算哈希值作为索引,若有冲突则直接在当前位置使用“头插法”即可。注意以下几点:
- 哈希值计算:对应
int型,key % table_size就可以直接当作哈希值。对于char*,则可以sum(key) % table_size当作哈希值。当前也有专门的哈希函数,但是由于需要频繁计算哈希值,在简单情况下,就采用上述处理即可。- 单个索引上的链表没有大小关系。所以查找/删除时需要遍历这个索引对应的整条链表。
就不单独写int型的代码并测试了,可以直接参考项目源码中的“hash.h”、“hash.c”。
2.6 dhash的实现
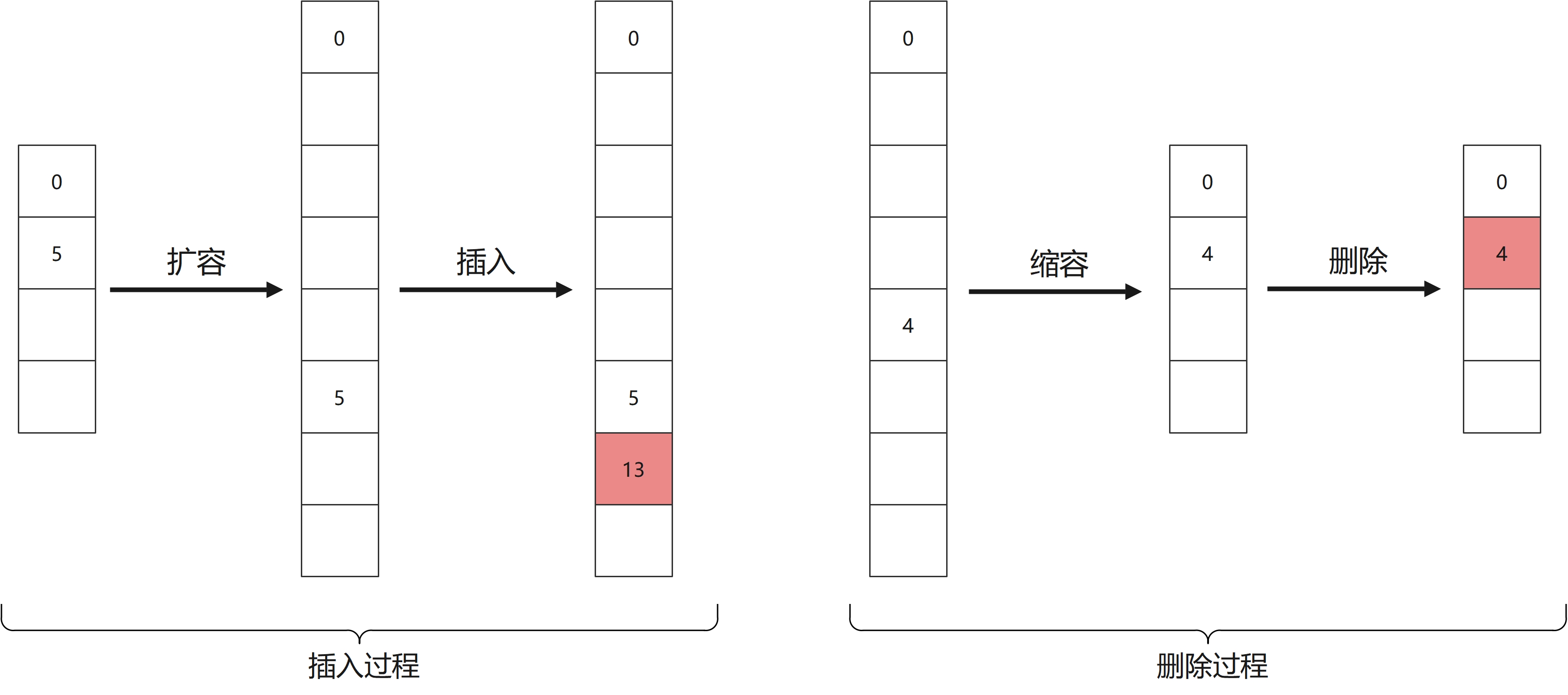
显然上述hash有个很大问题,就是“哈希表的大小”是固定的。如果声明哈希表大小为1024,却要插入10w个元素,那每个所有都会对应一个很长的链表,最坏的情况下和直接遍历一遍没什么区别!这显然失去了哈希的意义,于是在上面的基础上,我们使用“空间换时间”,自动增加/缩减哈希表的大小,也就是“动态哈希表”dhash:
- 插入元素时,首先判断是否需要扩容。若当前元素超过哈希表的1/2(自定义),则将哈希表翻倍(自定义),并将原来的元素重新映射到新的哈希表。若遇到冲突,则将新元素顺延插入到下一个空节点。
- 删除元素时,首先判断是否需要缩容。若当前元素小于哈希表的1/4(自定义),则将哈希表缩小一半(自定义),并将原来的元素重新映射到新的哈希表。若当前节点不是待删除元素,则需要从当前索引开始遍历完所有节点,才能说哈希表不存在此元素。
同样,不单独写int型的代码测试了,可以直接参考项目源码中的“dhash.h”、“dhash.c”。
2.7 skiplist的实现

跳表本质上是一个有序链表。红黑树每次比较都能排除一半的节点,这启发我们,要是每次都能找到链表最中间的节点,不就可以实现 O ( log N ) O(\log N) O(logN)的查找时间复杂度了嘛。于是如上图所示,我们不妨规定跳表的每个节点都有一组指针,跳表还有一个额外的空节点作为“跳表头”,那么每次都从顶层依次底层进行“跳”,就可以实现“每次比较都能排除剩下一半的节点”。但是还有个大问题,那就是上述理想跳表需要插入/删除一个元素时,元素的调整会非常麻烦,甚至还需要遍历整个链表来调整所有节点的指向!
所以在实际应用中,不会直接使用上述理想跳表的结构。而是在每次插入一个新元素时,按照一定概率计算其高度。统计学证明,当存放元素足够多的时候,该实际跳表性能无限趋近于理想跳表。
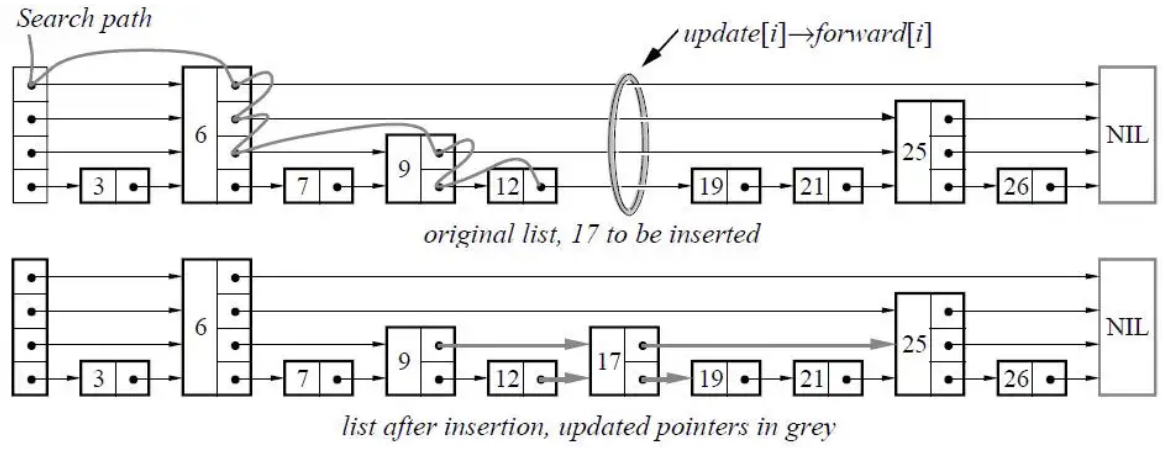
同样,代码直接见项目源码中的“skiplist.h”、“skiplist.c”。
2.8 kv存储协议的实现
如“1.2节-项目预期及基本架构”给出的“服务端程序架构”。现在我们实现了网络收发功能(网络层)、所有存储引擎的增删查改操作(引擎层),还差最后一个“kv存储协议”(协议层)就可以实现完整的服务端程序。“kv存储协议”的主要功能有:
- 初始化/销毁所有的存储引擎。这个直接调用各引擎的初始化/销毁函数即可。
- 拆解网络层接收的数据,若为有效指令则传递给相应的存储引擎函数处理,并根据存储引擎的处理结果返回相应的信息给网络层。
值得注意的是,“引擎层”的接口函数应该统一封装命名,并在各存储引擎中实现,“引擎层”的头文件中也只有这些接口函数暴露给“协议层”。这样保证了“协议层”和“引擎层”的隔离性,即使后续“引擎层”代码需要进行修改,也不会干扰到接口函数的调用、无需修改协议层。整个“服务端”的“网络层”、“协议层”、“引擎层”的函数调用关系如下:

同样,代码直接见项目源码中的“kvstore.h”、“kvstore.c”。
3. 性能测试
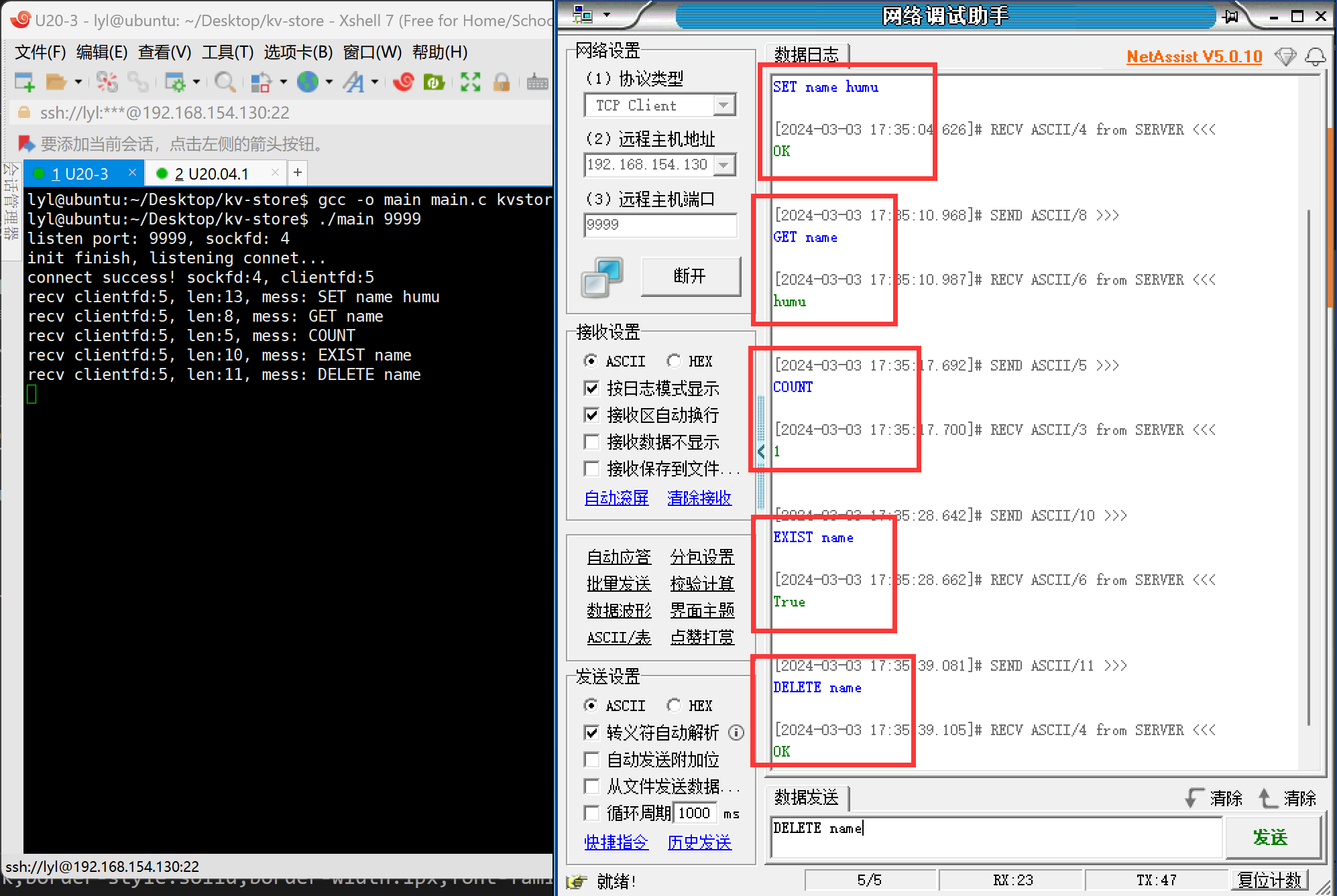
上述我们将“服务端”的代码实现完毕,并且可以使用“网络连接助手”进行正常的收发数据。如上图所示,依次发送5条指令后都得到预期的回复。但是我们要想测试客户端的极限性能,显然需要写一个“客户端”测试程序。该测试程序目标如下:
- 测试单个键值对(name:humu)能否正常实现所有功能。
- 测试多个键值对能否正常实现所有功能。这一步主要是为了验证各引擎能正常扩容/缩容。
- 测试连续进行10w次插入、查找、删除的总耗时,计算出服务器的相应速度qps。
注:测试代码直接见项目源码中的“tb_kvstore.c”。
如下图所示,开启两个Ubuntu虚拟机,分别运行“服务端”、“客户端”程序,得到如下的测试数据:
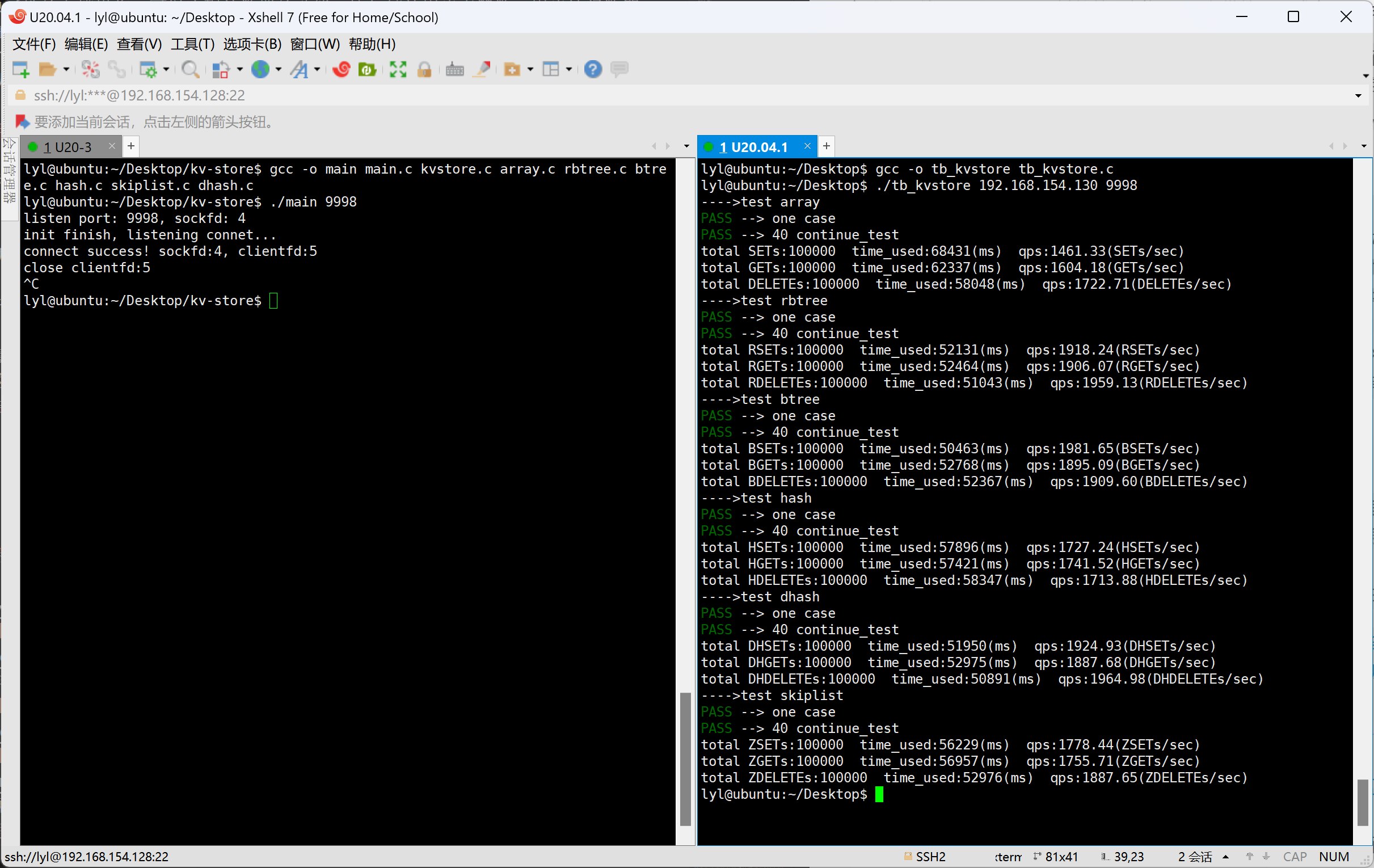
| 次数 | 操作 | qps(trans/s) | |||||
|---|---|---|---|---|---|---|---|
| array | rbtree | btree | hash | dhash | skiplist | ||
| 1 | 插入 | 1461.33 | 1918.24 | 1981.65 | 1727.24 | 1924.93 | 1778.44 |
| 查找 | 1604.18 | 1906.07 | 1895.09 | 1741.52 | 1887.68 | 1755.71 | |
| 删除 | 1722.71 | 1959.13 | 1909.60 | 1713.88 | 1964.98 | 1887.65 | |
| 2 | 插入 | 1570.13 | 1972.93 | 1949.62 | 1710.54 | 1926.63 | 1780.18 |
| 查找 | 1707.30 | 1970.40 | 1883.49 | 1709.46 | 2021.55 | 1747.89 | |
| 删除 | 1739.92 | 1918.80 | 1922.82 | 1730.28 | 1917.32 | 1912.74 | |
| 3 | 插入 | 1103.35 | 1898.25 | 1923.71 | 1737.59 | 1948.86 | 1794.24 |
| 查找 | 1316.59 | 1867.80 | 1933.38 | 1733.31 | 1953.74 | 1768.44 | |
| 删除 | 1774.78 | 1873.89 | 1978.98 | 1771.73 | 1966.76 | 1933.19 | |
| 4 | 插入 | 1134.22 | 1887.79 | 1888.72 | 1734.21 | 1909.53 | 1802.00 |
| 查找 | 1394.54 | 1908.80 | 1910.40 | 1726.43 | 1932.37 | 1764.76 | |
| 删除 | 1778.54 | 1897.97 | 1937.98 | 1719.25 | 1935.40 | 1928.57 | |
| 5 | 插入 | 1029.79 | 1981.02 | 1912.16 | 1718.33 | 1916.52 | 1777.62 |
| 查找 | 1236.52 | 1917.58 | 1947.00 | 1732.17 | 1934.39 | 1754.66 | |
| 删除 | 1703.87 | 1955.19 | 1899.59 | 1724.97 | 1915.42 | 1905.71 | |
结果分析:
- array引擎的指标都是最差的,这是因为每次插入/删除都需要遍历所有元素。
- hash引擎(链式哈希)的性能是倒数第二差的,这是因为虽然哈希函数可以快速定位到索引,但当键值对远大于哈希表大小时,冲突元素会形成一个链表,增/删/查操作也需要遍历整条链表。
- btree的插入性能好于rbtree,只是因为btree的单个节点可以容纳多个元素,节省了很多增加新结点、调整结构的时间;但是btree的查找/删除性能不如rbtree,也同样是因为单个节点还需要进行遍历。
- 综合来看,在10w次连续测试的场景下,最优秀的存储引擎是rbtree。
注:上述测试结果可以通过“相对值”比较各数据结构间的差异;“绝对值”则受限于虚拟机内存、运行频率等物理特性,并且网络层使用“协程”等也可以大幅提升“绝对值”。
4. 项目总结及改进思路
C/C++适合做服务器,但不适合做业务。因为可能会因为一行代码有问题,导致整个进程退出。虽然也能做,但维护成本高,并且对工程师要求高。比如“腾讯课堂”中课程、图片、价格等参数很适合用C语言做“kv存储”,但是显示网页等业务功能使用Jc语言更加合适。所以VUE框架(Java)等适合做前端业务;C/C++适合做基础架构、高性能组件、中间件。比如在量化交易中,底层的高频组件、低延迟组件适合用C/C++,上层的交易业务、交易策略没必要C/C++。
下面是对本项目的一些 改进思路:
- 持久化和日志:将数据都存储到(磁盘)文件中,并将接收到的指令记录下来成为日志。持久化的思路有很多种,比如直接分配一个大的“内存池”(见下一条)存放所有引擎的存储数据,然后直接对这个大的内存池进行持久化。
- 内存池:现在存储的数据都是零散的,比如rbtree每次插入新元素都会申请一个节点内存,时间长了就会出现很多内存碎片,不利于内存管理。理想状态是和数组结构体一样,直接预先声明一个内存池,需要新节点的时候就取出一个节点内存。这样,每次申请和释放的内存都是一整块,不会出现大量的内存碎片。
- 分布式锁:kv存储内部是单线程的,对于变量的改变无需额外加锁。但是外部的网络收发指令,需要引入分布式锁,防止多台客户端同时对同一个键值对进行修改。
- 主从模式:所有数据都存储在一台服务器上,会有丢失数据的风险,所以需要使用“主从模式”来对数据进行备份。关键点在于合适的备份策略。
- 分布式存储:所有数据都存储在一台服务器上,会导致内存压力过大,多台服务器结合起来做成“分布式存储”,所有服务器分摊数据。
编程感想:
- 字符串拷贝:C语言中,使用
strncpy、snprintf拷贝字符串时,注意目的字符串不能只是声明为char*,而是需要malloc/calloc分配内存才可以。另外也不要忘了释放内存free。- 天坑:解析指令时层层传递的是epoll的读缓冲
rbuffer,然后使用strtok/strtok_r进行分割指令并存储在char* tokens[]中,注意这个char* tokens[]的元素指向的就是读缓冲本身!!!而snprintf是逐字符进行拷贝的,也就是说,此时使用snprintf将tokens的内容再写回读缓冲就会导致读缓冲错乱。如果不额外分配内存很难解决该问题。所以建议不要使用snprintf拷贝自己的格式化字符串。- 良好的内存管理习惯:
free()之前先判断是否为NULL,free()之后一定要指向NULL。- 层层传递初始化:
【可行方法1】如果最顶层需要创建实例对象(不如全局变量),那就需要传地址给最底层,且最底层无需再重新为这个对象
malloc空间(因为最顶层已经创建对象了),只需要malloc好这个实例对象的所有指针即可,或者先定义成NULL后期插入时再分配。
【可行方法2】若最顶层无需创建全局的实例对象,那么也可以不传参数给最底层,最底层直接创建一个对象指针,并malloc/NULL这个对象指针的所有参数,最后直接返回这个对象指针就行。
【不可行方法】顶层创建了全局的实例对象,然后传地址给最底层,最底层重新malloc一个新的对象指针,初始化这个对象指针的所有参数,最后让传递下来的地址指向这个指针。最后在顶层就会发现所有参数都没初始化,都是空!
【关键点】:对谁进行malloc非常重要,一定要对顶层传下来的结构体指针的元素直接malloc,而不是malloc一个新的结构体,在赋值给这个结构体指针。
- 关于
strcmp():在使用strcmp()时一定要先判断不为空,才能使用。这是因为strcmp()的底层使用while(*des++==*src**),所以若比较的双方有一方为空,就会直接报错。- 注意项目的include关系,是在编译指令中指定的。当然也可以将“kv_store.c”中的case语句封装到各自的数据结构中,然后以动态库的方式进行编译。