994. 腐烂的橘子

题意:

在给定的网格中，每个单元格可以有以下三个值之一：

• 值 0 代表空单元格；
• 值 1 代表新鲜橘子；
• 值 2 代表腐烂的橘子。

每分钟，任何与腐烂的橘子（在 4 个正方向上）相邻的新鲜橘子都会腐烂。

返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1。

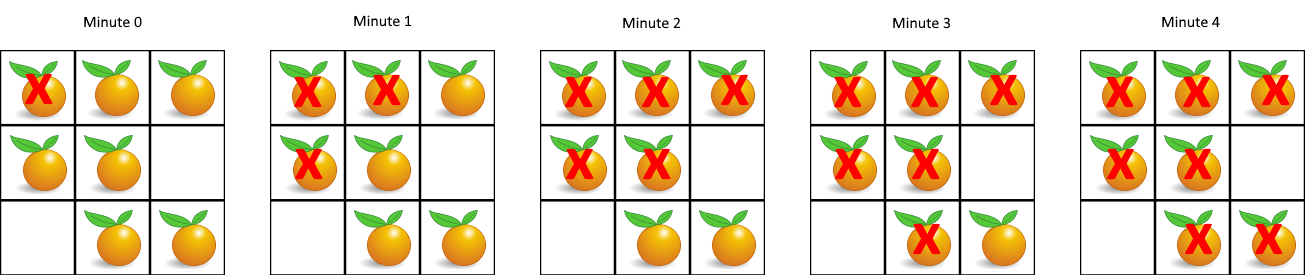
示例 1：

输入：[[2,1,1],[1,1,0],[0,1,1]]
输出：4

示例 2：

输入：[[2,1,1],[0,1,1],[1,0,1]]
输出：-1
解释：左下角的橘子（第 2 行， 第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个正向上

示例 3：

输入：[[0,2]]
输出：0
解释：因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。

解题思路:

这道题多源点的广度优先遍历,就是套用图广度优先遍历的题型,需要注意的几点为

1. 使用队列来存储源点.
2. 循环遍历矩阵时等于2就设置为源点,放入队列.打上标记. 等于0就直接打上标记
3. 循环直到队列为空,类似于层序遍历的操作.每一次都看队列有多少个节点,压入节点周围为1的值.打上标记.
4. 内层循环结束一次就让次数+1.
5. 循环结束后再遍历一次标记,如果标记矩阵没有全部标记.说明有橘子永远不会腐烂,就返回-1;
6. 题意最后一次不算,最终的次数需要 -1;如果num为0说明不用遍历,直接返回0.避免返回 0 - 1 的情况;

小tip:模板我全都记在另外一个文章中,✈如下:

❀算法模板❀

代码:

class Solution {
private:
    static constexpr int dirt[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
public:
    int orangesRotting(vector<vector<int>>& grid) {
	int n = grid.size();
	int m = grid[0].size();
	vector<vector<int>>flag (n, vector<int>(m, 0));
	queue<pair<int, int>> que;
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < m; j++)
		{
			if (grid[i][j] == 2)
			{
				que.emplace(i, j);
				flag[i][j] = 1;
			}
			else if (grid[i][j] == 0)
				flag[i][j] = 1;
		}
	}
	int num = 0;
	while (!que.empty())
	{
		int size = que.size();

		for (int index = 0; index < size; index++)
		{
			int i = que.front().first;
			int j = que.front().second;
			que.pop();

			for (int d = 0; d < 4; d++)
			{
				int ni = i + dirt[d][0];
				int nj = j + dirt[d][1];
				if (ni >= 0 && ni < n && nj >= 0 && nj < m && flag[ni][nj] != 1)
				{
					flag[ni][nj] = 1;
					que.emplace(ni, nj);
				}
			}
		}
		num++;
	}
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < m; j++)
		{
			if (flag[i][j] == 0)
				return -1;
		}
	}
	if (num == 0)
		return 0;
	return num - 1;
    }
};

总结:

这道题就是一个BFS的经典题型了,难点在次数的返回.需要判断是否全部都有节点都有标记 .有的话还需要判断是否需要遍历,不需要直接返回0,如果全都有标记和次数不为0,那么最终次数还需要减一.结果理清楚这道题难度就不大了