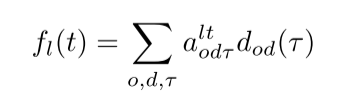Cyclic Graph Attentive Matching Encoder (CGAME)
Abstract
将多区间交通流量视为时空输入,将OD(original destination)矩阵视为异构图结构输出。
我们提出的 CGAME 是循环图注意匹配编码器的简称,它包括双向编码器-解码器网络,以及隐藏层中具有双层注意机制的新型图匹配器。它实现了前向网络和后向网络之间的有效信息交换,并建立了跨底层特征空间的耦合关系。
1、Introduce
在估计方法方面,卡尔曼滤波器(KF)、贝叶斯方法、广义最小二乘法(GLS)、最大似然法(ML)和基于梯度的技术[1]是以往工作中常用的方法。OD 估计可视为寻找下式解的过程[2]:
d o d ( τ ) d_{od}(τ) dod(τ) 表示在时间步骤 τ 从出发地 o 出发前往目的地 d 的旅行次数。
f l ( t ) f_l(t) fl(t) 给出了时间步 t 时链路 l 上的流量计数。
a o d τ l t a_{odτ}^{lt} aodτlt 是一个从 d o d ( τ ) d_{od}(τ) dod(τ) 到 f l ( t ) f_l(t) fl(t) 的映射张量,有 5 个索引:l、t、o、d、τ。
从 低纬度f 到 高纬度a ,无法直接求解。
除了少量特意设计的单层模型[5]外,该问题通常被建模为上层估计 OD 矩阵和下层进行动态交通分配(DTA)的分层结构,下层通常需要额外的输入或假设。
基于这种结构的大多数经典方法都依赖于特定的交通分配模型来建立 OD 流量与道路流量之间的联系。
路径选择过程有许多随即影响因素,以往的OD分配模型不准确
建立跨表示空间的映射是一项具有挑战性的任务,尤其是在道路网络拓扑结构复杂、车辆流量异构的情况下。
为了这项具有挑战性的任务构建一个神经网络框架,我们做出了三个假设。
- 首先,人口结构和城市布局不会在短期内发生重大变化。
- 其次,人们对路线选择的统计习惯可以在长期的历史出行数据中得到反映,这意味着从分配矩阵描述路径选择和出行分布概率的角度来看,在 OD 估算中并不一定需要明确的交通分配算法[6]。因此,在我们的工作中,通过应用逆编码器-解码器神经网络来捕捉从 OD 流量到链路上交通流量的映射,我们推出了一种无赋值矩阵的方法。
- 第三,连续时间间隔内的交通流量统计包含了该时间段内准动态 OD 矩阵的近似信息[7]。
循环图注意力匹配编码器(CGAME),这是一种在嵌入空间与注意力机制耦合的双向 "编码器-解码器 "网络。
主要贡献
- 我们提出了一种新颖的端到端神经网络方法来估算 OD,其中前向网络估算需求,后向网络挖掘行程分配的特征。
- CGAME 设计为循环生成架构,在嵌入空间中集成了双层注意力,使估算网络和动态流量分配网络能够在隐藏层中从各自的角度交换信息。
2、Literature Review
研究的主要区别:数据来源和估算方法
数据来源:
磁感应线圈摄像视频毫米波雷达、GPS、移动设备等,但是都需要进行后续的处理。
估算方法分为约束优化、迭代状态估算和基于梯度的技术。
约束优化指的是最大熵(ME)、最大似然估计(MLE)和广义最小二乘法(GLS)。
-
最大熵最早由文献[20]正式提出,这种方法用公式表示简洁方便,但其基于概率的性质并不能保证一定能得到正确的估计,也不能充分利用历史数据所蕴含的特征。
-
MLE [21]它在给定先验联合概率分布的情况下,
通过最大化观测值的可能性来估计 OD 矩阵。MLE 的主要缺点是需要交通需求的先验分布。此外,还需要因子来建立交通需求与相应观测值之间的映射关系,这可能会耗费大量计算资源。为了使数值计算更易求解,[22] 利用斯特林公式的近似值提出了简化版的 MLE。 -
GLS 是一种多变量最小二乘法,考虑了不同变量之间的协方差关系,
用于最小化估计 OD 与先验 OD 之间的误差,同时在赋值方程或不等式的限制下,最小化分配的交通流量计数与测量值之间的误差[23, 24]。然而,原始版本中数据提取的时间局部性可能会导致测量噪声,[25] 等人通过采用时间窗对 GLS 进行了扩展。除了单独应用这些方法外,一些研究还通过组合各种方法获得了更好的结果。例如,Xie 等人提出了 ME 和最小二乘法的组合形式,即 ME-LS。总的来说,这组方法理论性强,发展较早。然而,建模方法不可避免地依赖于相应模型的一些假设和约束条件,这可能会导致在某些复杂情况下估计性能的波动。
迭代状态估计主要指卡尔曼滤波及其变体。
- **卡尔曼滤波器(KF)**是利用一系列随时间变化的观测数据来迭代逼近真实的未知变量。[26]首次将 KF 引入 OD 估计,将其视为一个自回归过程。针对非线性问题的扩展卡尔曼滤波器自然成为 OD 估计问题的更好选择[27, 28]。
- 但迭代状态估计面临着误差随迭代积累的风险。为了保证结果的稳定性和鲁棒性,[7] 采用了准静态假设,将一段时间内的状态同时输入模型,这在一定程度上降低了迭代过程中的噪声。
- 对于大规模路网而言,这种使用矩阵乘法的方法对输入中的微小误差比较敏感,而且迭代方法或多或少会造成误差的累积,这使得该方法的应用受到限制。
基于梯度的技术包括同步扰动随机逼近(SPSA)和神经网络。
- SPSA 分离了目标 OD 估算和交通分配过程,通过随机逼近算法同时优化 OD 需求和交通流量[29-31]。然而对不同的OD行程应用同一套参数时,SPSA可能无法很好地收敛。为了解决这个问题,[32] 通过对应用聚类策略的 SPSA(即 c-SPSA)进行扩展,提高了 SPSA 的性能和鲁棒性。与 SPSA 中的显式梯度表达相比,神经网络采用了自动梯度反向传播机制,可以更灵活地设计模型框架,为这一复杂的非线性问题提供更强大的估计能力。
- 一些早期的神经网络工作如[33]利用 Hopfield 神经网络获得了行程矩阵,然后[2]利用神经网络创建了从链路流量和链路速度到行程生产和景点的映射,并将结果与基于 N 最短路径的行程分布相结合来估计 OD 矩阵。[17]设计了一种延迟受限的自动编码器来学习 OD 矩阵的去噪分解特征等。最后,为了更好地提取需求模式的特征,缓解大规模网络中维度诅咒的影响,在此问题中利用了主成分分析(PCA)[10, 34, 35]、CP 张量分解[36]、非负塔克分解[17]等辅助方法来降低维度。
3、Problem Statement
3.1 Problem Definition
我们的研究目的是,根据连续子时段内各连接点的交通流量,动态估算参考时段内的 OD 矩阵。
我们定义了一个由 n p n_p np 个点 P 1 、 P 2 … … P n p 和连接这些点的 n l 条链路 l 1 、 l 2 … … l n l P_1、P_2……P_{np} 和连接这些点的 n_l 条链路 l_1、l_2……l_{n_l} P1、P2……Pnp和连接这些点的nl条链路l1、l2……lnl组成的道路网络 G。
在一个周期 t 内,这些点之间的交通需求由 OD 矩阵 $ D∈R_{n_p×n_p} 表示,其中元素$ $ D(i, j) 代表从点 P_i 到 P_j $ 的出行次数。
通过将周期 t 分成 n t 个具有固定持续时间的子周期(标记为 t 1 、 t 2 … … t n t n_t 个具有固定持续时间的子周期(标记为 t_1、t_2……t_{n_t} nt个具有固定持续时间的子周期(标记为t1、t2……tnt,
交通流量计数矩阵 F ∈ R n l × n t 交通流量计数矩阵 F∈ R^{n_l×n_t} 交通流量计数矩阵F∈Rnl×nt中的元素 F(i, j) 表示子周期 t j 中链路 l i 的交通流量计数 t_j 中链路 l_i 的交通流量计数 tj中链路li的交通流量计数 。
本文尝试利用以历史数据训练的神经网络,以 F 为输入对 D 进行估计。
3.2 Overview
在一段时间内,行程从一个地点产生,并通过一系列链接汇入另一个地点,表示为
P
ϕ
o
→
l
α
1
→
l
α
2
−
−
→
l
α
η
→
P
ϕ
d
P_{ϕ_o} → l_{α_1} → l_{α_2} - - → l_{α_η} → P_{ϕ_d}
Pϕo→lα1→lα2−−→lαη→Pϕd 。考虑到时间因素,在子周期 $ t_β 时,链接 l_α 上的行程段可标记为(l_α, t_β)$ ,参数为 α 和 β,则行程的时空路线可以用序列表示:
r
k
:
=
[
P
φ
o
,
(
l
α
1
,
t
β
1
)
,
(
l
α
2
,
t
β
2
)
,
…
,
(
l
α
η
,
t
β
η
)
,
P
φ
d
]
r_{k}:=\left[P_{\varphi_{o}},\left(l_{\alpha_{1}}, t_{\beta_{1}}\right),\left(l_{\alpha_{2}}, t_{\beta_{2}}\right), \ldots,\left(l_{\alpha_{\eta}}, t_{\beta_{\eta}}\right), P_{\varphi_{d}}\right]
rk:=[Pφo,(lα1,tβ1),(lα2,tβ2),…,(lαη,tβη),Pφd]
将指定路线 $ r_k $ 上的出行次数定义为 $ n_{rk} $,那么该时间段内的所有出行次数就构成了一个向量
R
:
=
[
n
r
1
,
n
r
2
,
⋯
,
n
r
k
,
⋯
,
n
r
γ
]
\mathbf{R}:=\begin{bmatrix}n_{r_1},n_{r_2},\cdots,n_{r_k},\cdots,n_{r_\gamma}\end{bmatrix}
R:=[nr1,nr2,⋯,nrk,⋯,nrγ]
与 γ 的路线完全一致。而 F 和 D 的每个元素都可以表示为
F
(
i
,
j
)
=
∑
(
l
i
,
t
j
)
i
n
r
k
n
r
k
\begin{aligned}\mathbf{F}(i,j)&=\sum_{\begin{array}{c}(l_i,t_j)inr_k\\\end{array}}n_{r_k}\end{aligned}
F(i,j)=(li,tj)inrk∑nrk
D ( i , j ) = ∑ ( P φ O , P φ d ) = ( P i , P j ) n r k \begin{aligned}\mathbf{D}(i,j)&=\sum_{\big(P_{\varphi_O},P_{\varphi_d}\big)=(P_i,P_j)}n_{r_k}\end{aligned} D(i,j)=(PφO,Pφd)=(Pi,Pj)∑nrk
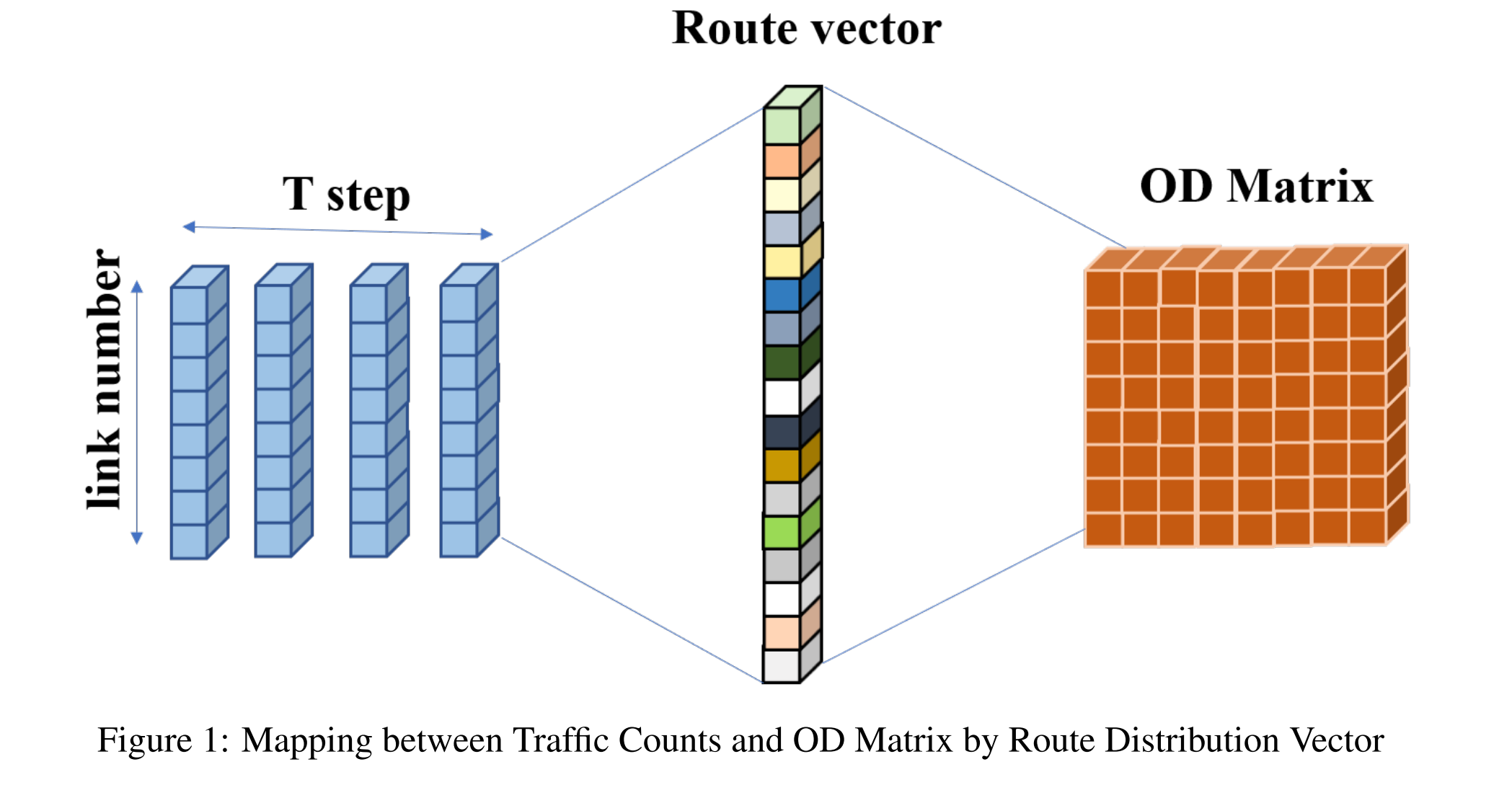
分别为从公式中我们可以看出,OD 矩阵反映的是景点之间的点间的图形结构,而交通流量则描述了出行的时空分布,图结构和时空分布的特征就像硬币的两面一样共存于路线向量 R 中。
如图 1 所示,OD 估算的关键在于通过路线分布向量 R 将这两面连接起来。在从 D 到 F 的方向上,动态交通分配会产生一个可能的路由分布 R’,而在反方向上,OD 估算会给出另一个可能的路由分布 R’‘。为了提高估算的准确性,应提高 R’ 和 R’’ 同一时间同一位置的出行的共现概率,直到 R’ 接近 R’'。然而,由于 $ r_k $ 结合了时空特征和图结构特征,当路网规模扩大时,路线分布向量γ 的维数将会增加到极高的程度。此外,由于 R 的稀疏性,双向近似将变得困难且有偏差。
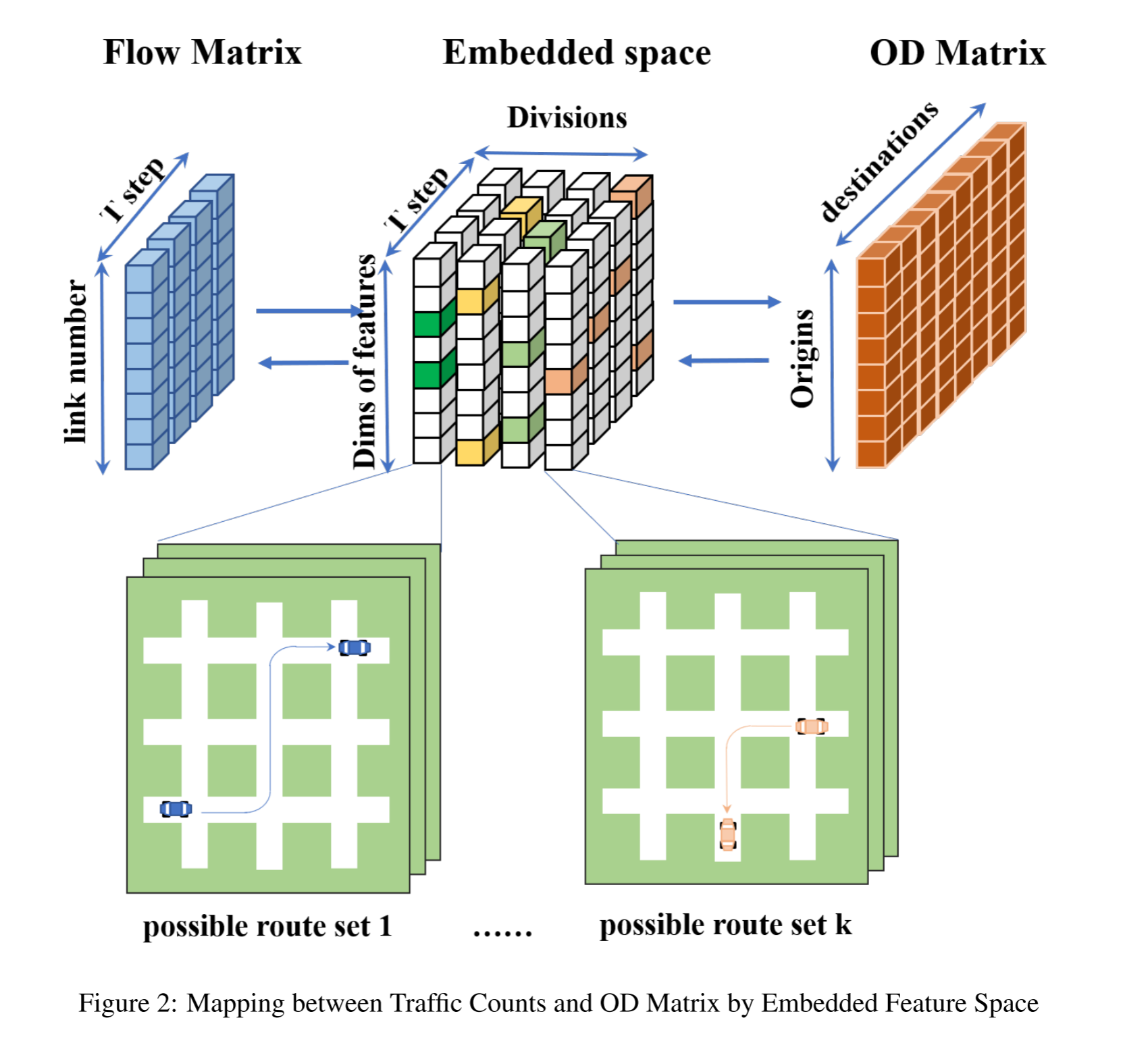
为了克服这些问题,我们将向量 R 压缩到有 n s n_s ns 个分区的嵌入空间,每个分区由 n f n_f nf 个特征组成,每个特征都可以看作是整个路线集 {r1 , r2 , ., rv} 的子集,那么 R’ 和 R’’ 之间的匹配关系就转为前向到后向捕获的特征向量之间的匹配关系。如图 2 所示, n s n_s ns 的划分起到了不同通道的作用。
4、Methodology
4.1 Overall architecture
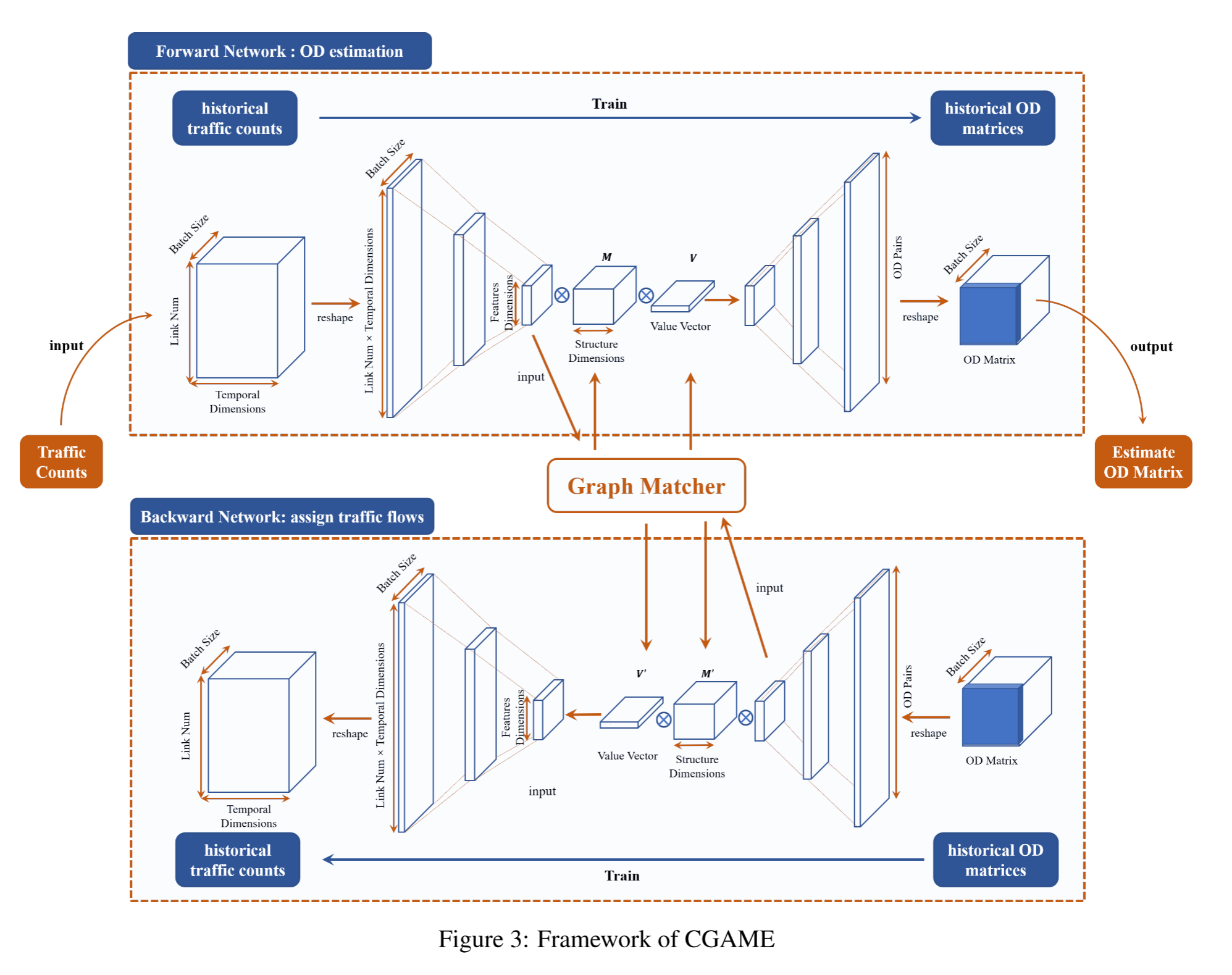
CGAME 由 3 个部分组成:前向编码器、后向编码器和图匹配层 3。
前向编码器和后向编码器均采用编码器-解码器框架,并共享中期匹配层,该层捕捉前向网络所代表的估算过程与后向网络所代表的流量分配过程之间的关系。
历史交通流量和历史 OD 矩阵被输入到网络训练中,前向网络学习近似 OD 矩阵。其中,历史 OD 矩阵可以根据历史人工调查结果获得,也可以从经过清洗和提取的车牌识别数据或交通流轨迹重建数据中获得。当所有这些数据源都缺乏时,我们可以对多个其他OD估计模型给出的闭合结果进行采样,并将其作为真实值来训练所提出的模型。
4.2 Encoder-Decoder Frameworks
在编码器-解码器架构中,我们采用多层感知器(MLP)将输入嵌入底层特征,并将底层特征解码为输出。
我们之所以采用多层感知器(MLP),而不是在捕捉时空特征方面表现出色的图卷积网络(GCN)和递归神经网络的组合,是为了让图匹配器能够以同质编码的方式更好地从不同方向获取底层特征。此外,作为一种谱图卷积,GCN 在共两层的情况下性能最好,而路由选择具有多跳范围广的特点,因此我们需要 MLP 来连接所有节点,找到路由分布。然后,编码器部分由两层 MLP 构建,表示为
h
x
=
LeakyReLU
(
W
2
(
LeakyReLU
(
W
1
x
+
b
1
)
)
+
b
2
)
h_x=\text{LeakyReLU}\left(W_2\left(\text{LeakyReLU}\left(W_1x+b_1\right)\right)+b_2\right)
hx=LeakyReLU(W2(LeakyReLU(W1x+b1))+b2)
W
1
、
W
2
、
b
1
、
b
2
是
M
L
P
的可学习参数,
x
是输入数据,
h
x
表示编码后的特征,其形状为批量大小
b
乘以特征尺寸
n
f
。
W1、W2、b1、b2 是 MLP 的可学习参数,x 是输入数据,h_x 表示编码后的特征,其形状为批量大小 b 乘以特征尺寸 n_f。
W1、W2、b1、b2是MLP的可学习参数,x是输入数据,hx表示编码后的特征,其形状为批量大小b乘以特征尺寸nf。
LeakyReLU 是一种常用的激活层,是整流线性单元(ReLU)的扩展。
结构匹配矩阵
M
∈
R
n
f
×
n
s
和结构信息矩阵
V
∈
R
1
×
n
s
由图匹配器给出
结构匹配矩阵 M∈R^{n_f×n_s} 和结构信息矩阵 V∈R^{1×n_s} 由图匹配器给出
结构匹配矩阵M∈Rnf×ns和结构信息矩阵V∈R1×ns由图匹配器给出,注意力操作由以下公式表示:
g
x
=
m
e
a
n
n
s
(
h
x
⊙
∣
∣
b
M
⊙
∣
∣
b
,
n
f
V
)
g_x=mean_{n_s}(h_x\odot||_bM\odot||_{b,n_f}V)
gx=meanns(hx⊙∣∣bM⊙∣∣b,nfV)
其中,
⊙
\color{green}{\odot}
⊙表示哈达玛乘积算子,在此过程中利用了广播机制;
∣
∣
b
||_{b}
∣∣b 表示在批量维度上的复制操作,
∣
∣
b
,
n
f
||_{b,n_f}
∣∣b,nf表示在批量维度和特征维度上的复制操作;
m
e
a
n
n
s
mean_{n_s}
meanns 计算结构维度上的平均值。
h
x
,
g
x
h_{x},g_{x}
hx,gx 是编码器的输出和解码器的输入。关于 M 和 V 的表示和获取的更多细节将在下文中介绍。
解码器还包括双层 MLP,将注意
g
x
g_x
gx 后的特征向量映射到输出:
y
=
LeakyReLU
(
W
3
(
LeakyReLU
(
W
3
g
x
+
b
3
)
)
+
b
4
)
y=\text{LeakyReLU}(W_3(\text{LeakyReLU}(W_3g_x+b_3))+b_4)
y=LeakyReLU(W3(LeakyReLU(W3gx+b3))+b4)
类似的编码器-解码器被应用于两个方向。
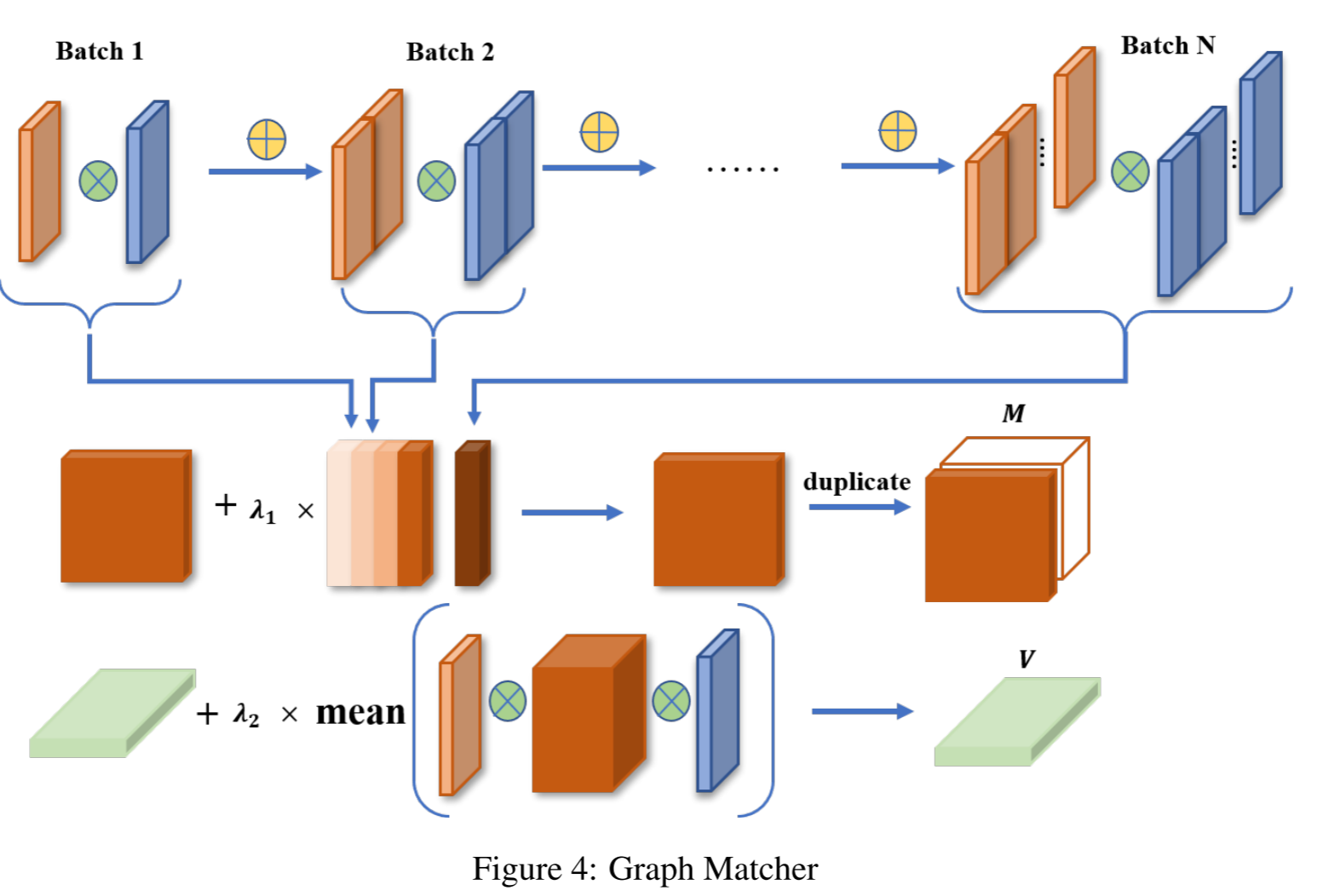
4.3 Graph Match Layer
结构匹配矩阵 M 对正向和反向编码特征 h x h_x hx和 h y h_y hy进行匹配,并从不同角度(即结构)形成多重匹配。结构值矩阵 V 根据匹配质量对结构进行权衡,并赋予不同结构不同的通过率。一开始,M 和 V 都被初始化为填充 1 的矩阵,代表具有相同通过率的统一结构。
M 的每一步更新都由
n
s
n_s
ns 个子步骤组成,每个子步骤都会计算沿批次维度的变化相似度,其内在逻辑是不同侧面的相似特征以类似的方式变化。具体来说,前向编码器和后向编码器的编码特征之间的相似性被分解为不同范围的匹配,即结构。在第 j 步的第 p 个子步骤中,将 p 批编码特征串联起来,计算结构匹配矩阵
M
j
:
M_j{:}
Mj:的响应列中的结构:
M
j
(
:
,
p
)
=
(
1
−
λ
m
)
⋅
M
j
(
:
,
p
)
+
λ
m
⋅
∑
p
⋅
b
(
h
x
⊙
h
y
)
∑
p
⋅
b
(
h
x
⊙
h
x
)
∑
p
⋅
b
(
h
y
⊙
h
y
)
\begin{gathered}M_j(:,p)=(1-\lambda_m)\cdot M_j(:,p)+\lambda_m\cdot\frac{\sum_{p\cdot b}(h_x\odot h_y)}{\sqrt{\sum_{p\cdot b}\left(h_x\odot h_x\right)}\sqrt{\sum_{p\cdot b}\left(h_y\odot h_y\right)}}\end{gathered}
Mj(:,p)=(1−λm)⋅Mj(:,p)+λm⋅∑p⋅b(hx⊙hx)∑p⋅b(hy⊙hy)∑p⋅b(hx⊙hy)
其中,
M
j
(
:
,
p
)
M_j(:,p)
Mj(:,p) 表示结构匹配矩阵 M 的第 p 列。
⊙
\odot
⊙ 为哈达玛乘积,
∑
p
⋅
b
\sum_{p\cdot b}
∑p⋅b 为 p · b 个数据样本的批量维度上的和。相应地,结构值矩阵 V 的第 p 列更新为
V
j
(
p
)
=
(
1
−
λ
m
)
⋅
V
j
(
p
)
V_j(p)=(1-\lambda_m)\cdot V_j(p)
Vj(p)=(1−λm)⋅Vj(p)
结构值矩阵 V 衡量 $ h_y $与 $ h_x^{\prime}$ 之间的相似度,其中后者表示每个结构操作的编码特征向量 $ h_x $,因此 V 的更新由以下公式给出:
V
j
=
∑
n
f
(
(
∥
n
s
h
x
)
⊙
M
j
⊙
(
∥
n
s
h
y
)
)
∑
n
f
(
(
∥
n
s
h
x
)
⊙
M
j
)
2
∑
n
f
(
∥
n
s
h
y
)
2
+
λ
v
V
j
V_j=\frac{\sum_{n_f}\left((\|_{n_s}h_x)\odot M_j\odot(\|_{n_s}h_y)\right)}{\sqrt{\sum_{n_f}\left((\|_{n_s}h_x)\odot M_j\right)^2\sqrt{\sum_{n_f}\left(\|_{n_s}h_y\right)^2}}+\lambda_vV_j}
Vj=∑nf((∥nshx)⊙Mj)2∑nf(∥nshy)2+λvVj∑nf((∥nshx)⊙Mj⊙(∥nshy))
其中, ∣ ∣ n s ||_{n_s} ∣∣ns 沿结构维重复编码向量, ∑ n f ( ⋅ ) \sum_{nf}(\cdot) ∑nf(⋅)是特征维的和, dim , ( ∣ ∣ n s h x ) ⊙ \dim,(||_{n_s}h_x)\odot dim,(∣∣nshx)⊙ M j M_j Mj 处理编码特征向量 h x h_x hx,生成 h x ′ h_x^{\prime} hx′ 序列, V j V_j Vj主要计算这些 h x ′ h_x^{\prime} hx′与 h y h_y hy之间的余弦相似度。计算中采用了广播机制。最后一项表示上一个子步骤的折扣权重值。
4.4 Loss Function
我们比较了深度学习中的两个经典损失函数:L1 Loss 12 和 MSE Loss 13,前者可以直观地衡量估计值与真实值之间的车辆数量差异,后者则可以限制过大的差异。根据应用目的,损失函数可以选择其中之一。
L1 Loss
=
∣
y
t
−
y
^
t
∣
\text{L1 Loss}=|y_t-\hat{y}_t|
L1 Loss=∣yt−y^t∣
M S E L o s s = ( ∣ ∣ y t − y ^ t ∣ ∣ ) 2 \mathrm{MSE~Loss}=\left(||y_t-\hat{y}_t||\right)^2 MSE Loss=(∣∣yt−y^t∣∣)2
5、Experiments
5.1 Description
我们在两个网络中评估了我们的模型:一个是 6 × 6 网格网络,另一个是现实的城市道路网络。我们使用一个广泛使用的模拟器 SUMO 对交通网络进行了模拟。
在这两个场景的模拟中,车辆被分为 5 类,它们具有不同的大小和动态特性,包括普通轿车、慢车、快车、公交车和卡车。在车辆动态参数、路线选择和模拟级别中配置了随机性。
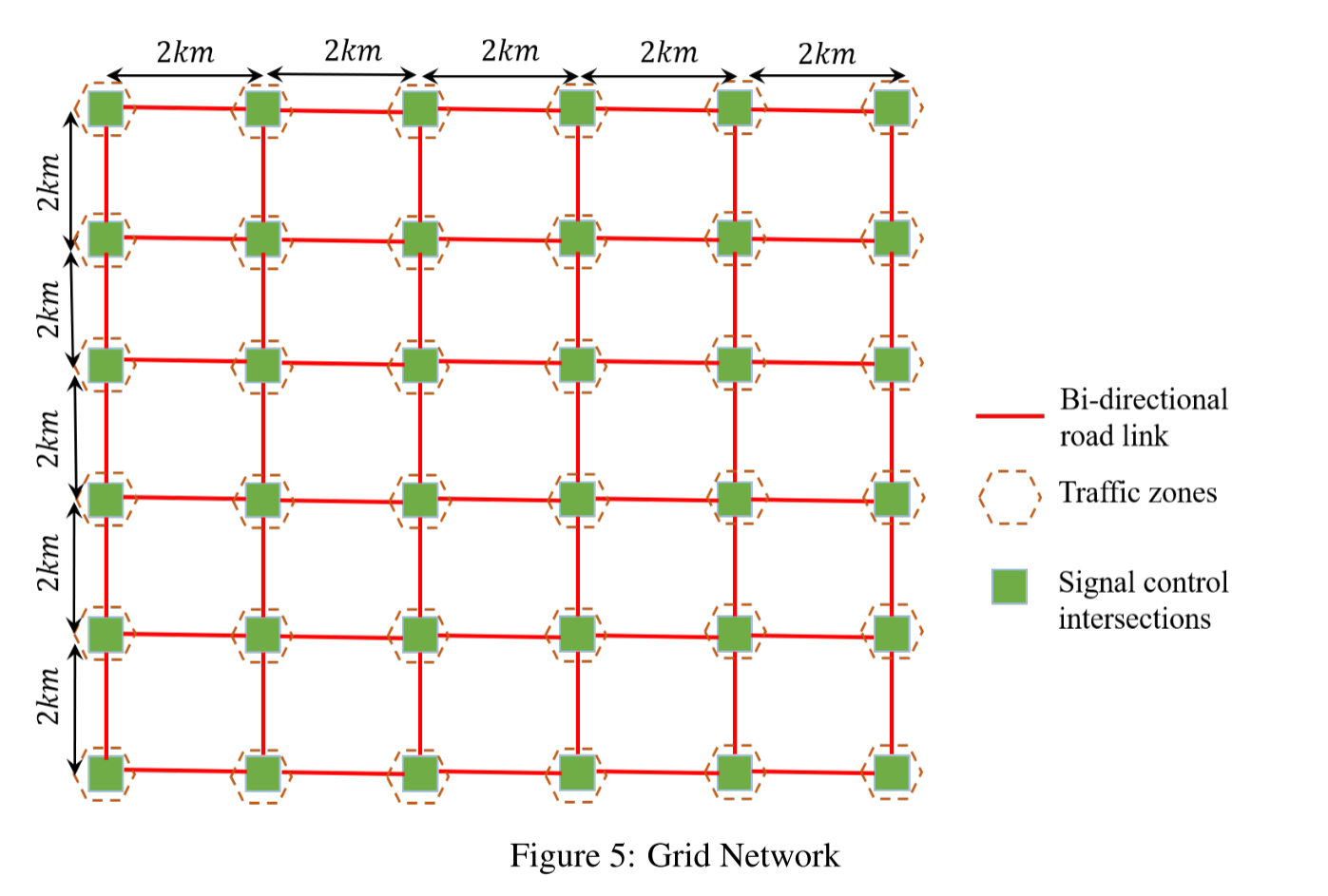
5.1.1 Scenario 1: Grid Networks
图 5 所示为网格网络,其中有 120 条 4 车道连接线和 32 个信号交叉口。每条连接线的长度为 2 公里,交叉口包括 16 个 T 形交叉口和 16 个十字路口。每条连接线的起点周围有 36 个交通区,车辆从这些交通区出发或到达这些交通区。然后,我们构建 20 个基本 OD 矩阵,作为交通区之间的基本交通需求模式,并在每轮模拟中叠加 20% 的扰动后,随机取样其中一个矩阵,将其作为真实的总体 OD 矩阵。
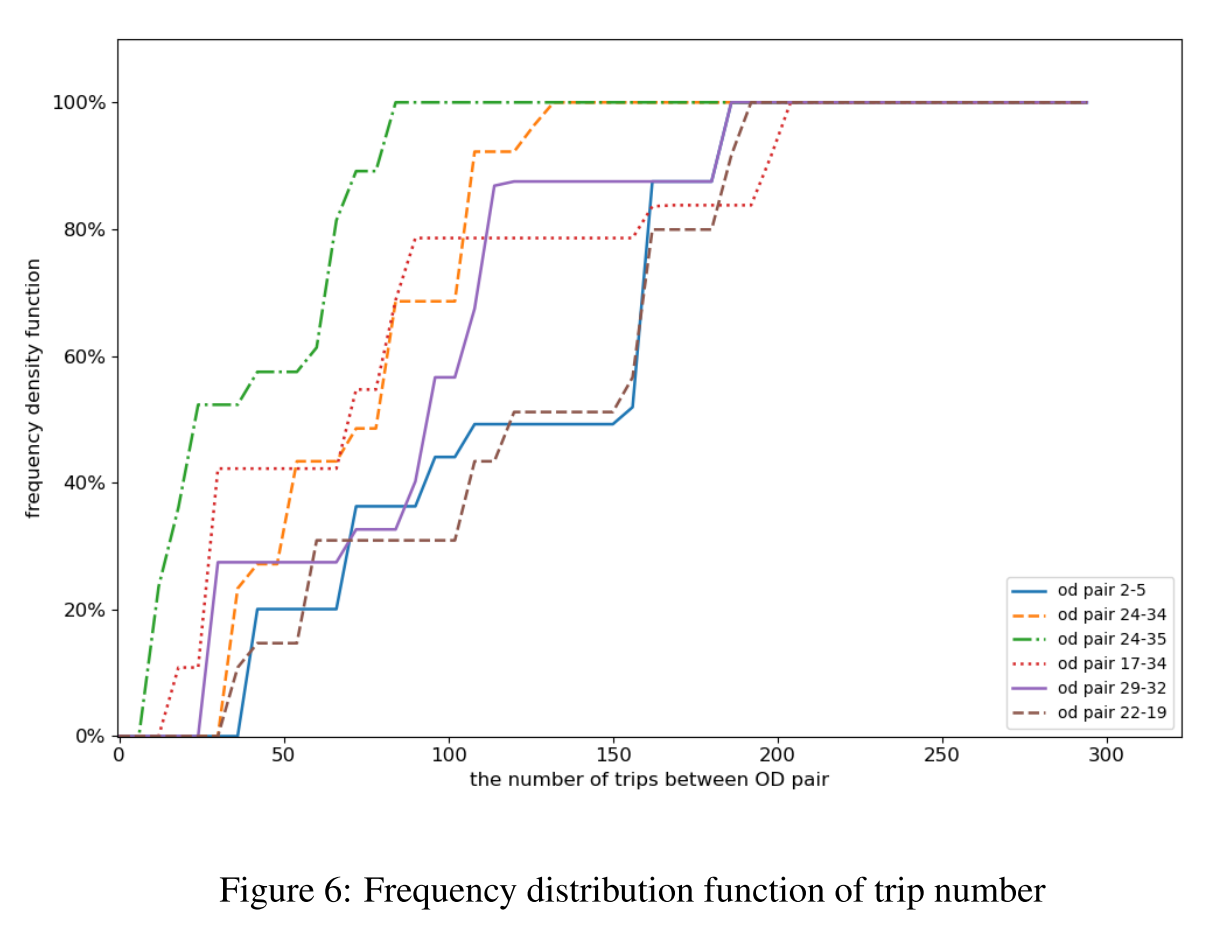
具体来说,图 6 给出了在不同模拟轮次中随机抽取的 OD 对之间的出行次数频率分布曲线。
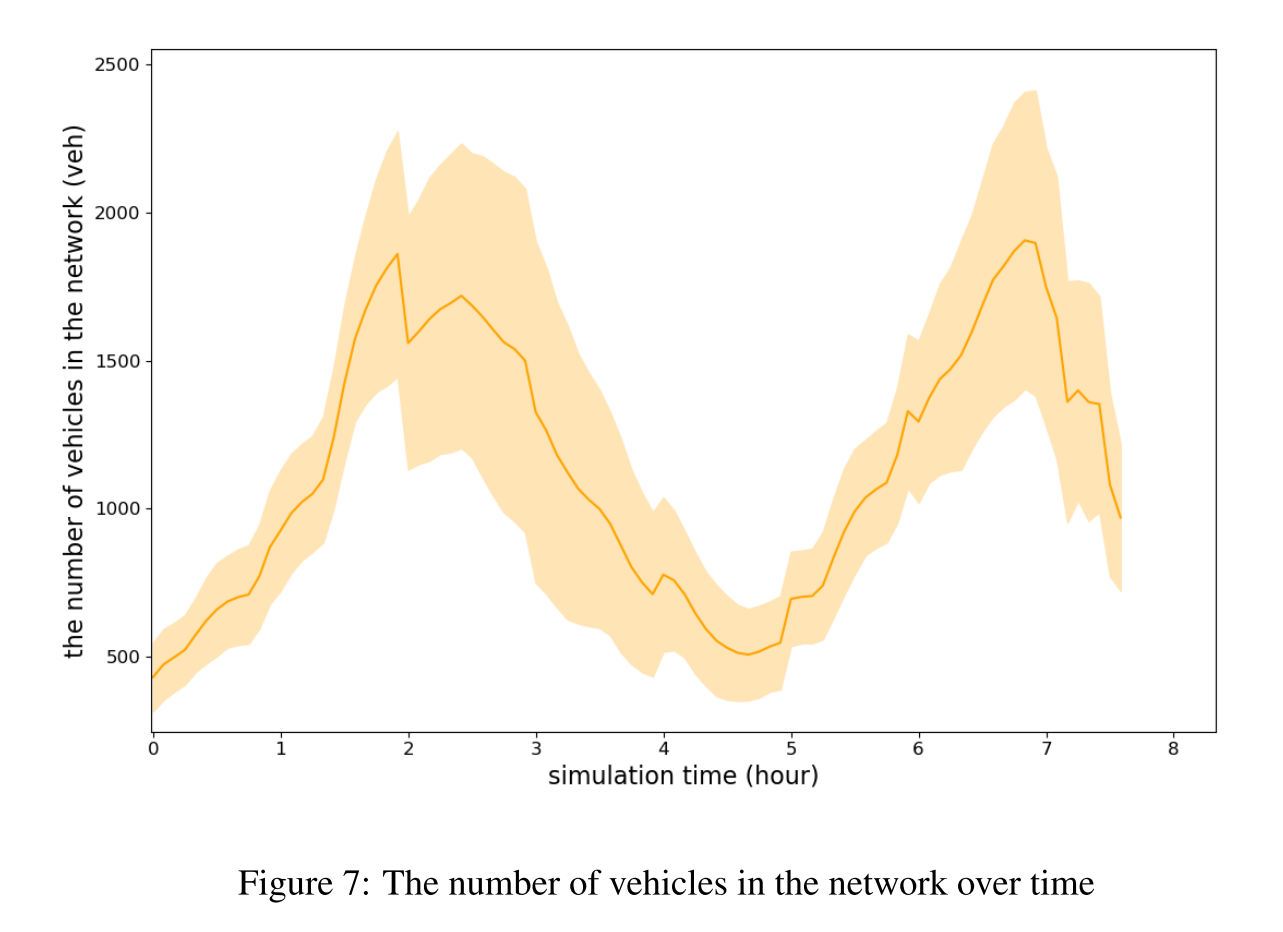
在整个模拟过程中,所有行程都是在一定概率下随机选择出发时间的,有两个峰值。我们将每小时从一个地点到另一个地点的次数,作为随时间波动的实时每小时 OD 矩阵,并通过观测进行估算。观测数据给出了每小时内路网中每 5 分钟经过每个连接点的车辆数。交通流量随时间的波动可以用路网中车辆总数的曲线来表示,如图 7 所示。
此外,考虑到驾驶员选择路线的不同原则,模拟中的路线选择有两种配置方式。在给定起点和终点的情况下,
-
一种是以相对固定的概率分布选择路径,
-
另一种是根据驾驶员对最短行车时间的感知实时调整路径选择。前者的比例为 70%,后者为 30%。
交通区之间所有非故意绕行的路线都预先设计成路线集,驾驶员从中选择路线。
每轮模拟涉及 30000 模拟秒,我们记录了从 2400 秒到 27600 秒共 7 小时的交通流量和 OD 矩阵。因此,在每一轮模拟中,我们利用 7 个形状为 12 × 120 的交通流量矩阵来估算 7 个小时的 OD 矩阵。流量统计矩阵由从 120 个链路测得的 12 个连续的 5 分钟数据组成。模拟总共运行 1000 轮,获得 7000 个数据样本,其中 800 轮模拟作为训练集,200 轮作为测试集。
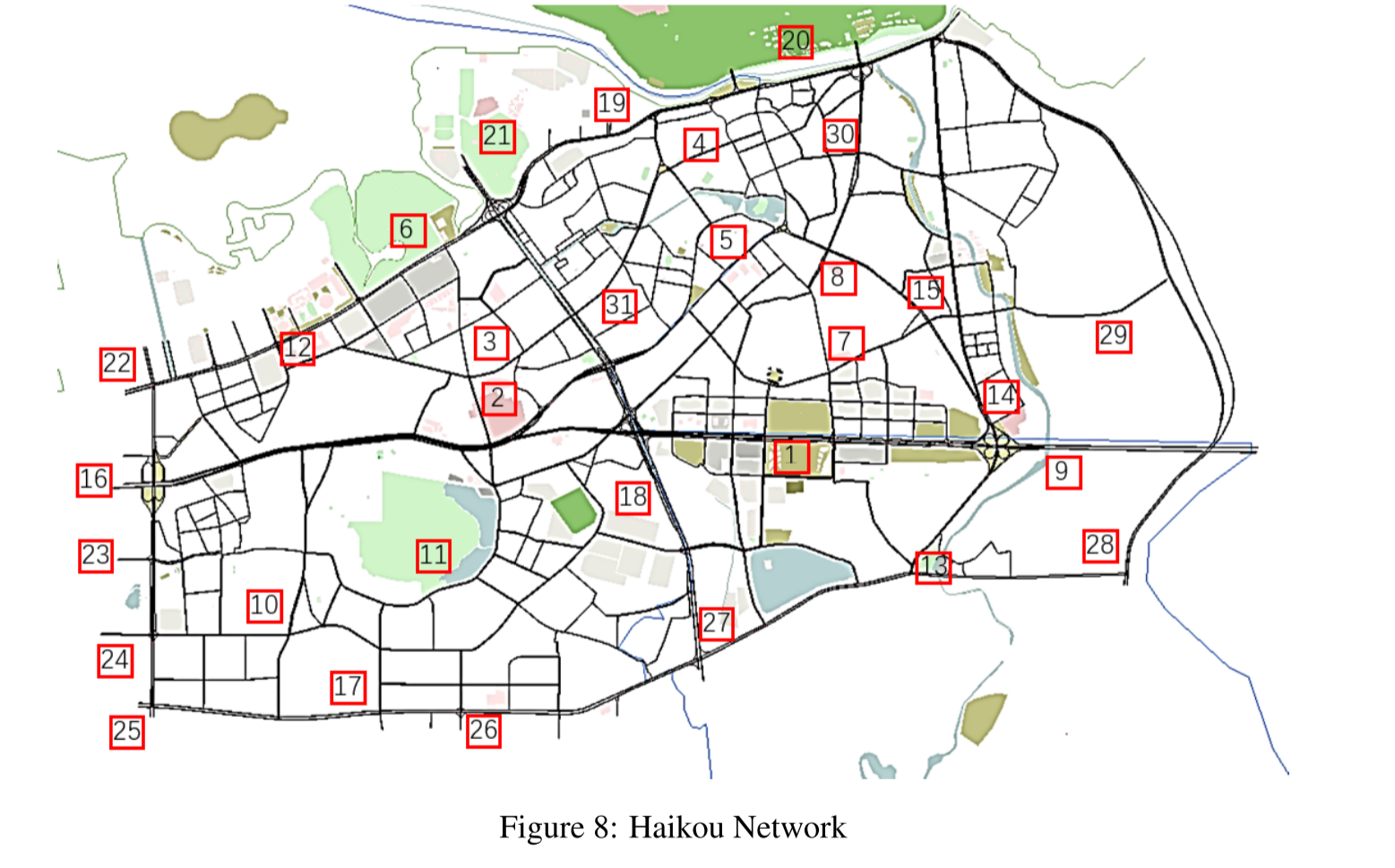
5.1.2 Scenario 2: Realistic Urban Road Networks
另一个场景选择了中国海口市中心城区的一个真实城市路网,面积为 10km×6km ,包括 2328 个连接点和 1171 个交叉口。在 359 个交通流量较大的路段设置了环路,以测量交通流量。在我们的模拟中,不同城市功能区的交通流量产生和吸引随时间呈现出不同的变化,如早高峰时段住宅区交通流量产生大,商业区交通流量吸引大,晚高峰时段则出现逆向 OD 流量。除此之外,作为一个中等人口的城市,海口市中心还涵盖了其他几类典型的出行需求。具体来说,比如早上去公园晨练或买菜的人,晚上去夜市的人,周五放学回家的学生等。而购物中心则成为周末的热门旅游目的地。在此基础上,我们手动配置每周的时变出行需求,并在每一轮模拟中以一定的随机性对其进行排列。
一天内的模拟时间从早上 5:20 到晚上 10:20,分为 6 个时段:早晨、早高峰、中午、下午、晚高峰和夜间。考虑到稳定过程,我们在估算 OD 时使用的数据是从早上 6 点到晚上 10 点的采样数据,其中包括每小时的 OD 估算数据和 12 个 5 分钟的交通流量计数,如上一方案所述。模拟运行 400 轮,产生每天 16 小时的 400 天数据。经过归一化和随机排列后,90% 的数据作为训练集,10% 作为测试集。请注意,在测试时,结果都是去规范化的。
5.2 Evaluation metrics
评估结果的指标如下:
a) Root Mean Square Error (RMSE)
R M S E = 1 N ∑ i = 1 N ( y i − y ^ i ) 2 \mathrm{RMSE}=\sqrt{\frac1N\sum_{i=1}^N\left(y_i-\hat{y}_i\right)^2} RMSE=N1i=1∑N(yi−y^i)2
b) Mean Absolute Error (MAE)
Мае = 1 N ∑ i = 1 N ∣ y i − y ^ i ∣ \text{Мае}=\frac1N\sum_{i=1}^N|y_i-\hat{y}_i| Мае=N1i=1∑N∣yi−y^i∣
c) Mean Absolute Percentage Error (MAPE)
M A P E = 100 % N ∑ i = 1 N ∣ y i − y ^ i ∣ ∣ y i ∣ \mathtt{MAPE}=\frac{100\%}N\sum_{i=1}^N\frac{|y_i-\hat{y}_i|}{|y_i|} MAPE=N100%i=1∑N∣yi∣∣yi−y^i∣
d) Coefficient of Determination (R2)
R 2 = 1 − ∑ i = 1 N ( y i − y ^ i ) 2 ∑ i = 1 N ( y i − y ˉ ) 2 R^2=1-\frac{\sum_{i=1}^N\left(y_i-\hat{y}_i\right)^2}{\sum_{i=1}^N\left(y_i-\bar{y}\right)^2} R2=1−∑i=1N(yi−yˉ)2∑i=1N(yi−y^i)2
其中,N表示来自测试集合的数据样本的数量, y i y_i yi表示OD矩阵中元素的实际值, y ^ i \hat{y}_i y^i是模型的相应估计值, y ˉ i \bar{y}_i yˉi 是 y i y_i yi的平均值
RMSE和MAE衡量实际OD矩阵与估计值之间的差异,而MAPE则量化两者之间的相对偏差。 R 2 R^{2} R2代表相关系数,描述了数据趋势的相关性。
5.3 Benchmark Model
我们选择了四种基线方法:两种常规方法和两种基于神经网络的方法。
- [32]中提出的聚类-SPSA(c-SPSA)方法,遵循本研究的思想,将聚类核的个数选择为三个。
- 扩展卡尔曼滤波(EKF),它是广泛应用于OD估计的卡尔曼滤波的非线性扩展。
- 经典的时空神经网络,它是图卷积网络(GCNS)和时间卷积网络(TCNs)的结合。
- 循环生成对抗性网络(CycleGAN)起源于计算机视觉中的风格迁移问题,其结构类似于所提出的具有前向和后向两个编码者的网络。
5.4 Results and Analysis
5.4.1 Measures of Performances
表2显示了CGame和Baseline在网格和实际网络中的4个指标上的性能,其中*表示负值,表明相关性R2的性能较差。结果表明,CGame在栅格网和实际路网中均获得了最小的均方根误差、最大均方根误差和最大均方根误差,而精度最高。在网格网络中,CGame的均方根误差和均方根误差分别下降到0.46和0.30,而在实际网络中,CGame的均方根误差和均方误差在4左右。对于大多数交通需求研究来说,这些误差都很小,不会影响数据质量,这意味着CGame获得的OD数据可以在很多领域得到应用。两种情况下的相对误差MAPE分别为2.78%和15.09%,进一步印证了这一分析。在第二种情况下,拟议模型的性能下降的原因可能包括稀疏而不是完整的交通计数测量以及路网结构的复杂性增加。此外,为了最大程度地模拟市中心日常出行的交通行为,考虑了不同目的和不同类型路线选择的各种需求。总体而言,在所有测试场景中,我们的模型的结果都比基准测试得到了显著的改进。这两个神经网络框架在两个测试场景中得到了相似的结果,但它们在OD估计问题上的表现都不像在原来的应用领域那样令人满意,说明了CGame在将深度学习引入交通需求估计问题方面的鼓舞人心的前景。在我们的实验中,在交通需求随时间波动的情况下,EKF的性能较差主要是由于对固定分配矩阵的依赖和状态迭代过程中误差的积累。作为一种基于梯度的优化方法,c-SPSA被应用于许多高级的需求估计研究中,只要交通分配模型是准确的,该方法就具有很高的精度,并且在我们的实验中,它确实取得了所有基准测试中最好的性能结果。
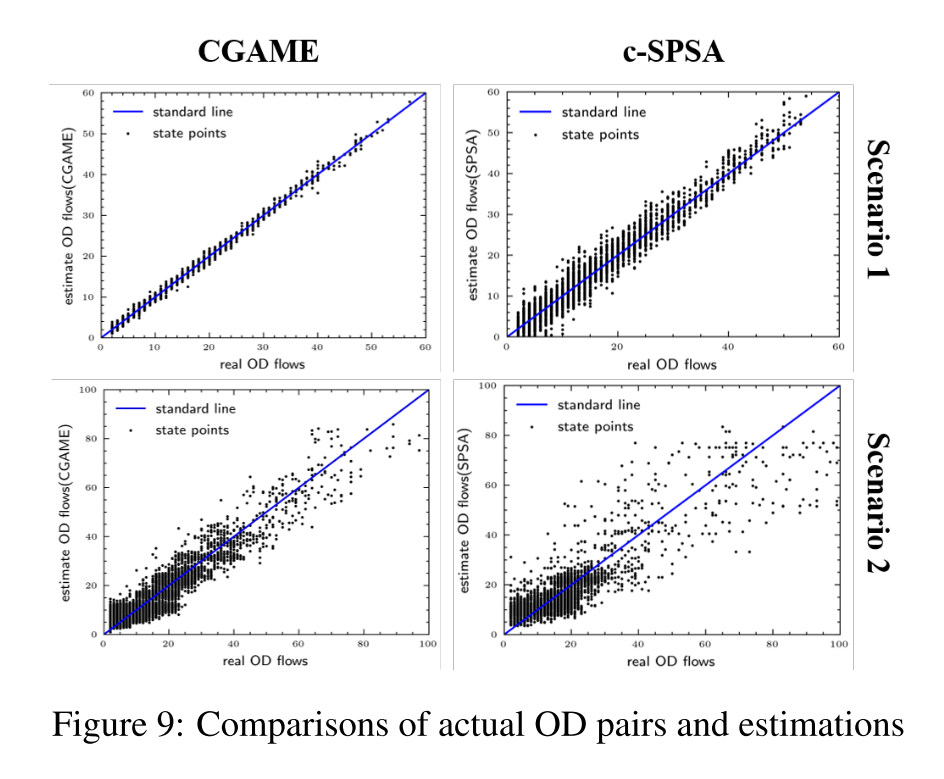
图9显示了GCome的估计能力和关于交通需求的最佳性能基准c-SPSA。我们随机抽取了3000对实际OD值及其相应的估计值,即状态点。45◦倾角的标准线表示100%准确的估计,状态点越接近标准线,它们的精度就越高。如本章第一部分所述,在规则网格路网且所有道路的交通计数都是可观测的情况下,CGame表现出极高的精度,并且实验结果不存在过拟合,因为测试集和训练集是严格分离的,并且在每一轮仿真中都存在多种随机性产生机制。
5.4.2 Comparison between actual OD matrices and estimations
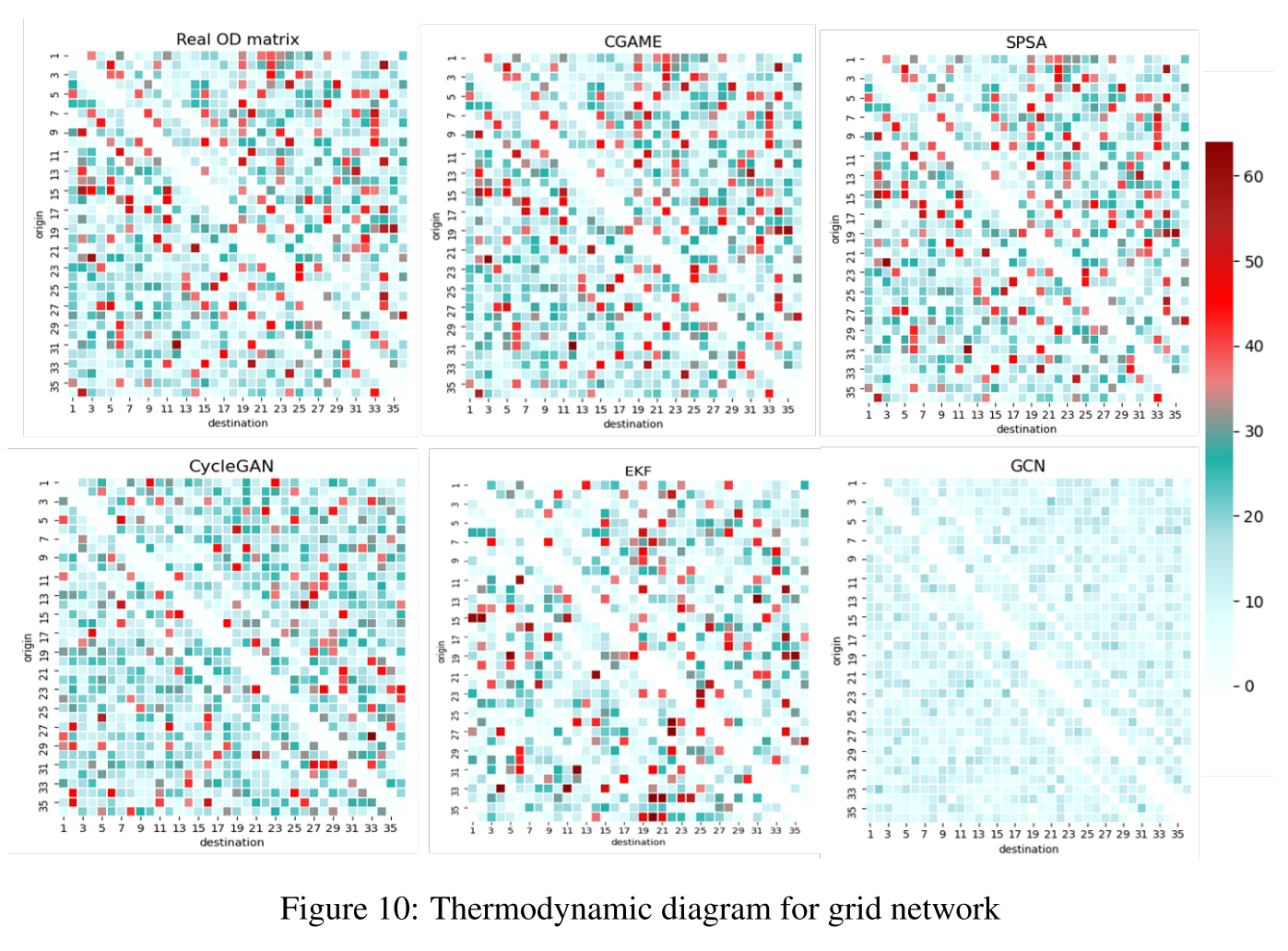
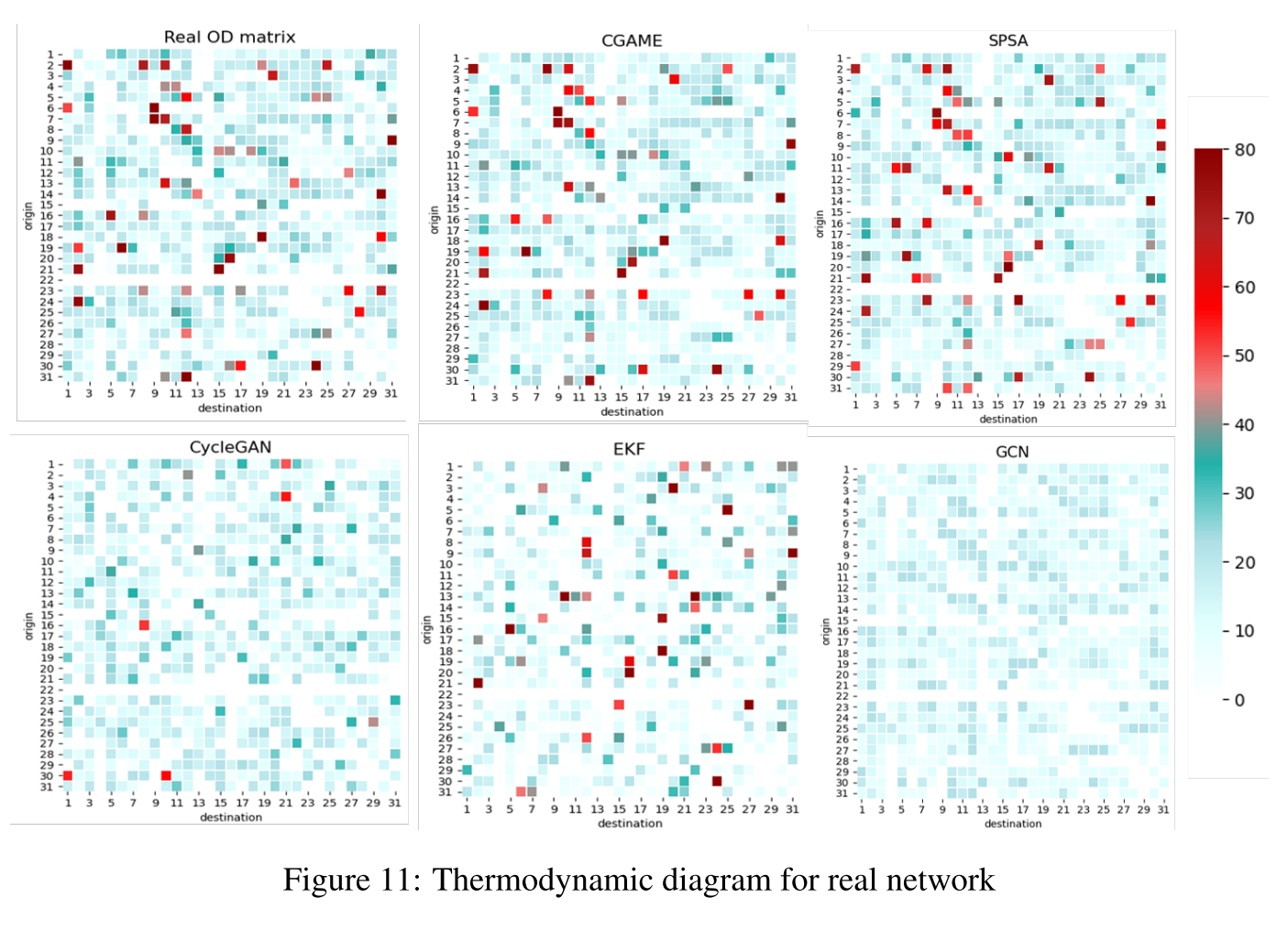
为了更直观地呈现结果,我们给出了实际OD和估计OD的热力学图,如图10和图11所示。
像素的颜色量化了OD对之间的交通需求强度。通过规定OD流量不能发生在交通区域内或相邻交通区域之间,这可以直观地理解为在一个交叉口产生OD出行,并在下一个交叉口下沉,因此在图10中OD矩阵的对角线周围有三条零值斜线。
图中的其他一些点,即“异构点”,如读取的像素,在图中值得注意。它们的交通需求强度与相邻像素的交通需求非常不同,这给模型捕捉这些点带来了挑战,而这些点在许多情况下是不可忽视的,甚至是至关重要的。
例如,这些突出点的信息在交通管理中对公平分配交通资源起着不可或缺的作用。图表显示,我们提出的模型和c-SPSA都能够识别这些离群点,CycleGAN和EKF也产生了这些非齐次点,但它们的分布与实际OD矩阵中的分布并不完全匹配。在训练CycleGAN的过程中,我们发现即使经过微调,鉴别器的损失仍然比生成器的损失小得多。由于生成过程是一个复杂的跨空间数据转换过程,很难与判别过程达到动态平衡,这限制了GAN算法在本课题中的实施。另一方面,GCN和TCN生成的图像更平滑,低需求OD对的主要组成掩盖了高需求点的捕获,这意味着这种深度学习架构更适合提取交通需求的整体而不是详细分布。在卡尔曼滤波中,状态的迭代是由多步矩阵乘法组成的,导致矩阵中的元素容易过大或过小,因此需要历史需求数据来校准迭代过程。对于我们的模型,虽然表2在场景2中表现出衰减,但不影响所提出的模型描述了交通需求的总体趋势和详细分布,因此它是理想的在OD估计领域的应用。
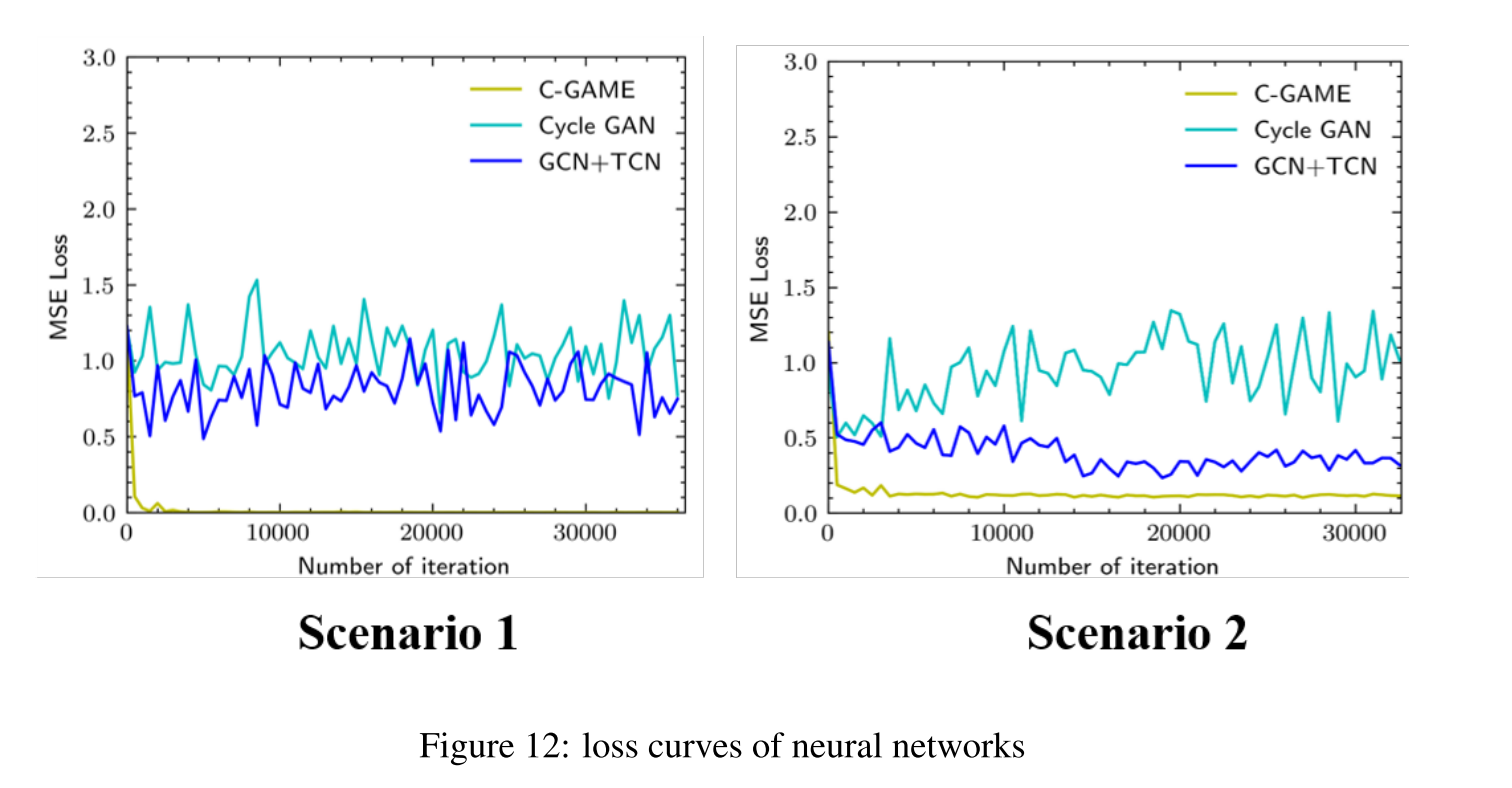
5.4.3 Loss Curve
图12显示了三个神经网络GCN、CycleGAN和CGame的训练过程。整个训练过程包括36000次迭代,所提出的模型在第1000次迭代时收敛。RTX 2060上的计算时间都在40分钟左右。
6、Conclusion
该研究开发了一种新颖的神经网络框架来解决OD估计问题,其中包括一个用于OD估计的前向编码器、一个用于提取流量分配模式的后向编码器,以及一个在前向和后向学习之间交换信息的双层注意机制。通过引入梯度传播通过率的概念,该框架可用于 OD 估算等跨空间推理问题。所提出的神经网络框架还可以推广到许多其他类似的推理问题中。
我们用四个基线评估了模型的性能,并得出了最佳性能。在 SUMO 的帮助下,考虑到保真度,我们将测试平台配置为 6×6 网格网络和海口市的真实大小网络。在实验中我们发现,通过部分连续的交通流量观测,可以准确估计 OD 矩阵。然而,路网拓扑结构的复杂性也会影响 OD 估算的准确性。在复杂的现实城市路网中进行精确的交通估算需要设计良好的模型和相对完整的历史数据。在模型评估方面,能否准确预测高需求的OD对是评估OD估计模型性能的重要指标,而本文提出的模型在近似交通需求方面表现出了令人满意的准确性。
未来的研究方向包括利用本地观测到的交通需求数据研究该架构的性能。我们发现,当历史交通需求中存在缺失值或随机噪声时,模型的性能不会明显下降。通过改变架构中两个编码器的结构,如使用 GCN、TCN 和 CNN,该模型可以扩展到更大规模的道路网络。此外,该架构还可应用于许多其他领域,如交通流量预测、交通需求预测等。