ABC210: E - Ring MST #最小生成树# #数学#
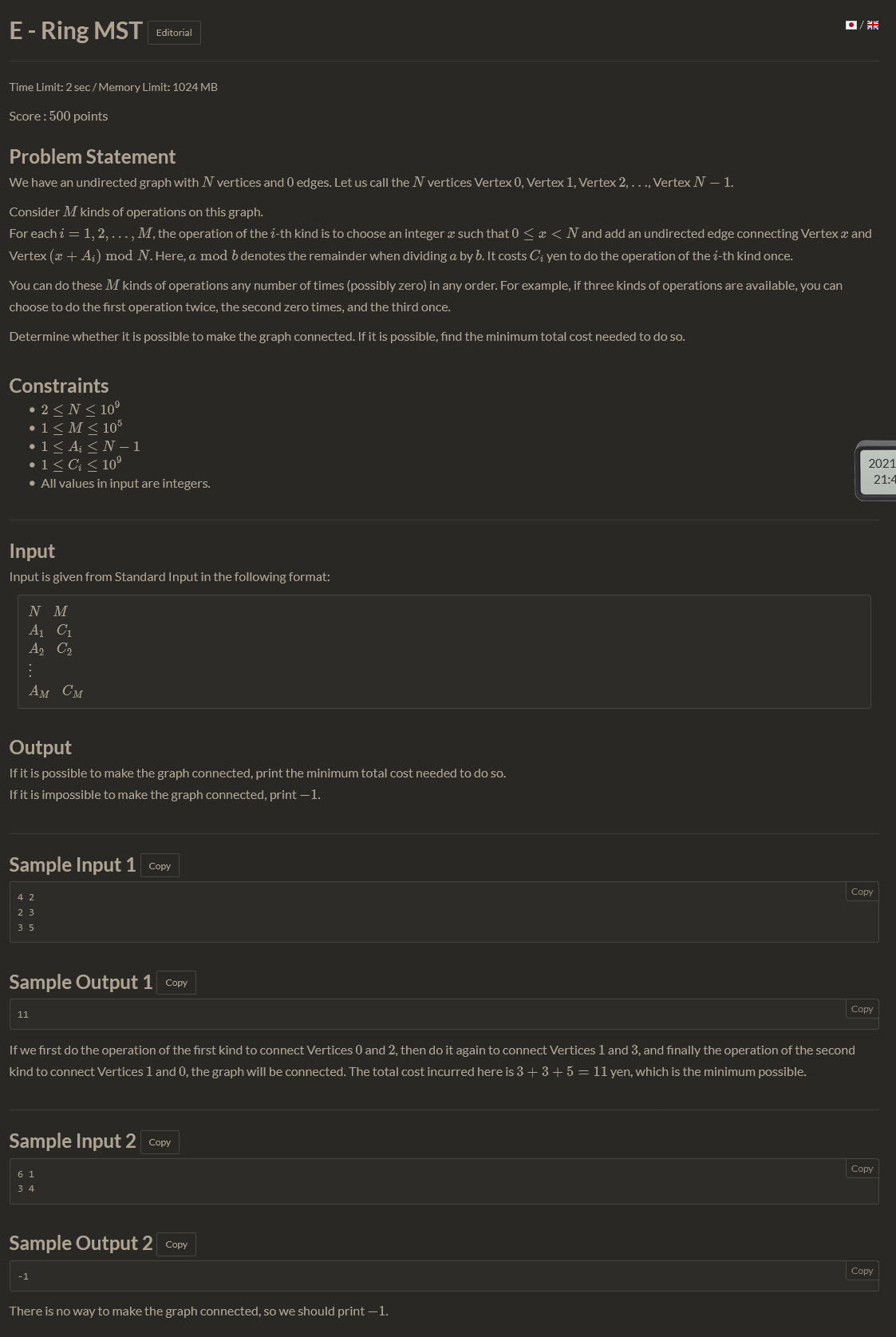
题目
大意:给定
n
n
n个点(编号
0
0
0~
n
−
1
n-1
n−1),
m
m
m种无向边,第
i
i
i种边可以连接点
x
,
(
x
+
a
i
)
m
o
d
n
(
0
≤
x
≤
n
−
1
)
x,(x+a_i)\mod n(0\le x\le n-1)
x,(x+ai)modn(0≤x≤n−1)用一次的花费为
c
i
c_i
ci,求将图变成一个连通块的最小花费
思路
不难想到,这题是最小生成树,而且是
K
r
u
s
k
a
l
Kruskal
Kruskal(边数较小,点数巨大)
不管三七二十一,先把边按
c
i
c_i
ci单调递增排序.
再想想,费用越小的边,肯定用得越多越好(在能连接不同连通块的前提下).如果我们知道,在已经连上费用更小的边的情况下,一种边在有意义(能连接两个不同的连通块)的前提下最多能用多少次,那这题不就A了吗?
难点就在这里.
我们设加上前
i
i
i种边后(已排序),图中最少有
x
i
x_i
xi个连通块.
特别地,
x
0
=
N
x_0=N
x0=N,显然,答案就是:
∑
i
=
1
m
c
i
⋅
(
x
i
−
1
−
x
i
)
\sum ^m_{i=1}c_i\cdot (x_{i-1}-x_{i})
i=1∑mci⋅(xi−1−xi)
当
x
n
>
1
x_n>1
xn>1时,无解,输出-1
所以如何求
x
x
x?
根据题意,在加入前
i
i
i种边后,点
w
w
w和
u
u
u在同一个连通块内,当且仅当:存在正整数序列
k
1
,
k
2
,
k
3
,
⋯
k
i
k_1,k_2,k_3,\cdots k_i
k1,k2,k3,⋯ki,使得
w
=
(
u
+
∑
j
=
1
i
k
i
⋅
a
i
)
m
o
d
n
w=(u+\sum ^i_{j=1}k_i\cdot a_i)\mod n
w=(u+∑j=1iki⋅ai)modn,即
w
=
u
+
∑
j
=
1
i
k
i
⋅
a
i
+
k
0
⋅
n
(
k
0
∈
Z
)
w=u+\sum ^i_{j=1}k_i\cdot a_i+k_0\cdot n(k_0\in \Z)
w=u+∑j=1iki⋅ai+k0⋅n(k0∈Z)
变换一下:
k
0
⋅
n
+
k
1
⋅
a
1
+
k
2
⋅
a
2
+
⋯
+
k
i
⋅
a
i
+
u
−
w
=
0
k_0\cdot n+k_1\cdot a_1+k_2\cdot a_2+\cdots+k_i\cdot a_i+u-w=0
k0⋅n+k1⋅a1+k2⋅a2+⋯+ki⋅ai+u−w=0
其中,
n
,
a
n,a
n,a已知,
k
k
k都是整数但未知,判断是否存在一组合法的
k
k
k,这是什么?斐蜀定理!!!
所以,
w
,
u
w,u
w,u连通,当且仅当,
gcd
(
n
,
a
1
,
a
2
,
⋯
,
a
i
)
∣
u
−
w
\gcd(n,a_1,a_2,\cdots,a_i)|u-w
gcd(n,a1,a2,⋯,ai)∣u−w,(
x
∣
y
x|y
x∣y表示
x
x
x能整除
y
y
y)
即
w
≡
u
(
m
o
d
gcd
(
n
,
a
1
,
a
2
,
⋯
,
a
i
)
)
w\equiv u(\mod \gcd(n,a_1,a_2,\cdots,a_i))
w≡u(modgcd(n,a1,a2,⋯,ai)),余数有
0
,
1
,
2
,
⋯
gcd
(
n
,
a
1
,
a
2
,
⋯
,
a
i
)
−
1
0,1,2,\cdots\gcd(n,a_1,a_2,\cdots,a_i)-1
0,1,2,⋯gcd(n,a1,a2,⋯,ai)−1共
gcd
(
n
,
a
1
,
a
2
,
⋯
,
a
i
)
\gcd(n,a_1,a_2,\cdots,a_i)
gcd(n,a1,a2,⋯,ai)种,所以共
gcd
(
n
,
a
1
,
a
2
,
⋯
,
a
i
)
\gcd(n,a_1,a_2,\cdots,a_i)
gcd(n,a1,a2,⋯,ai)个连通块
所以
x
i
=
gcd
(
n
,
a
1
,
a
2
,
⋯
,
a
i
)
x_i= \gcd(n,a_1,a_2,\cdots,a_i)
xi=gcd(n,a1,a2,⋯,ai)
所以我们就做完了
官方题解:
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;
int read() {
int re = 0;
char c = getchar();
bool negt = false;
while(c < '0' || c > '9')
negt |= (c == '-') , c = getchar();
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0' , c =getchar();
return negt ? -re : re;
}
const int M = 100010;
int gcd(int a , int b) {
return b == 0 ? a : gcd(b , a % b);
}
struct node {
int a , c;
}ed[M];
bool cmp(node a , node b) {
return a.c < b.c;
}
int n , m;
int x[M];
signed main() {
n = read() , m = read();
for(int i = 1 ; i <= m ; i++)
ed[i].a = read() , ed[i].c = read();
sort(ed + 1 , ed + m + 1 , cmp);
x[0] = n;
for(int i = 1 ; i <= m ; i++)
x[i] = gcd(x[i - 1] , ed[i].a);
if(x[m] > 1)
puts("-1");
else {
long long ans = 0;
for(int i = 1 ; i <= m ; i++)
ans += 1ll * (x[i - 1] - x[i]) * ed[i].c;
cout <<ans;
}
return 0;
}